一类非线性二阶泛函微分方程解的振动性

范良君,郑文娟



一类非线性二阶泛函微分方程解的振动性

范良君,郑文娟

(常德职业技术学院现代教育技术中心,湖南常德, 415000)

用数学分析的有关技巧获得了一类非线性二阶泛函微分方程解的振动性的若干条件, 推广了相关文献的一些结果, 扩大了相关定理的适用范围。

非线性; 泛函微分方程; 振动性; 正商

文献[1–5]对微分方程(ⅰ) (()(¢()))¢+()(()) = 0, (ⅱ) (()(¢()))¢+()((())) = 0, (ⅲ) (()|¢()|- 1)¢())¢+()((())) = 0,(ⅳ) (())¢())¢+()((()))(¢()) = 0的振动性做了研究, 并获得一系列结果, 本文运用数学分析的有关知识, 采用直接分析的方法研究了较方程(ⅱ)更为广泛的方程

(()(())(¢()))¢+()((())) =(()), (1)

获得了该方程解的性态的若干条件, 推广了有关文献的某些结论。

为简单起见, 假定0 <=/,为偶数,为奇数;()≥0且不恒为0,()为最终正函数, 0 <0≤()≤< ∞,且¢() ≥ 0;满足性质(ι)() > 0 (≠ 0), (ιι)¢() ≥ 0;满足() < 0 (≠ 0)。

称一个非平凡函数()为方程(1)的一个解是指()满足方程(1)。这个解()振动是指它是某半直线[0, ∞]上有定义且零点为无数界集, 否则称为不振动的。若方程(1)的所有解振动, 则称方程(1)是振动的。为了方便, 总假定所考虑的函数在其定义域内连续。

1 引理

文献[1–5]中的结论, 考虑了方程(ⅳ)对是分母且为奇数的有理分数时解的振动性。

引理1 假设(H1)() > 0 (≠ 0), 且¢() ≥0;(H2) 存在常数> 0, 使得()≥;(H3); (H4); (H5)¢() ≥0, 且() ≤; (H6)。则: (a)为奇数时,方程(ⅳ)振动; (b)为偶数时,方程(ⅳ)的解或者振动,或者有非振动解存在,且当()是最终正解时,; 当()是最终负解时,。

证明 设()是方程(ⅳ)的一个非振动解, 由方程(ⅳ)有

由定理的条件可知()不振动时,¢()也不振动。先证明为奇数奇数时结论成立。

(I) 设≥0≥0时,() > 0且(()) > 0。

情形1 当≥1≥0时,¢() > 0且¢(()) > 0。

由方程(ⅳ)有

对式(2)由1到积分得

。 (3)

由式(2), (3), 当≥1时, 有

故

。 (5)

结合方程(ⅳ)可知

()(¢())+()(¢())- 1¢¢() +()((()))(¢()) = 0。 (6)

于是结合定理的条件及≥1时,¢() > 0可得: 当≥ 1时¢¢() ≤ 0, 从而0 <¢()≤¢(())。

再由(6)式有, 当≥1时,

对(7)式由1到积分可得

。 (8)

由条件可知→+∞时, (8)式的左端为+∞, 与右端为有限数矛盾。

情形2 当≥1≥0时,¢() < 0且¢(()) < 0。

由(H2)知, 当>1时, (()(¢()))¢+()((()))≤ (()(¢()))¢+()((()))(¢()), 从而由方程(ⅳ)得, 当≥1时,

(()(¢()))¢≤-()(()((())) < 0, (9)

对(9)式由1到积分, 得()(¢())≤(1)(¢(1)), 有

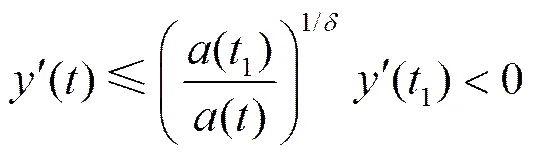
对(10)式由1到积分有。由定理中条件可知, 当充分大时, 必有()≤0, 与假设() > 0矛盾。

(Ⅱ) 设≥0≥0时,() < 0, 且(()) < 0。

情形1 当≥1≥0时,׳() > 0且׳(()) > 0,此时(4)～(8)式仍然成立, 可类似导出矛盾。

情形2 当≥1≥0时,׳() < 0且׳(()) < 0。

2 主要结论及定理

定理1 设

, (12)

(13)

成立, 则方程(1)的任意有界解()振动或单调趋于0。

证明 要不然, 设()为方程(1)的有界非振动解, 由方程(1)知:

(i) 当() < 0时, (()(())(¢()))¢≤ 0且()(())(¢())≥ 0;

(ii) 当() < 0时, (()(())(¢()))¢≤ 0且()(())(¢())≥ 0。故若除׳() ≡ 0外, 不可能有׳()振动的情形。因此只须考虑(i)() < 0且¢() > 0;

(iii)() > 0且¢() > 0;

(iv)() > 0且¢() < 0, 其中≥0。

由方程(1)得恒等式

下面分别讨论上述4种情形:

情形(i)() < 0, 且¢() > 0,≥0。

对式(15)从1到积分有

, (16)

经积分得

。 (18)

由式(13)知式(18)的右边随→∞而趋于无穷大, 与左边为负数矛盾。

情形(ii)() < 0且¢() < 0,≥0。

(()(())(¢()))¢-()(-) –(())≥0。 (19)

对式(19)从到1积分有, 因而有。

经积分得

由式(13)知式(20)的右边随→∞而趋于无穷大, 与左边为有界数矛盾。

情形(iii)() > 0, 且¢() > 0,≥0。由式(14)得式(16), 再由式(11)知式(16)的右边随→∞而趋于无穷大, 与左边为正矛盾。

情形(iv)() > 0, 且¢() < 0,≥0。若, 则已证, 若不然, 则及1≥0, 使得≥1时,() >, 从而有((()))≥() > 0, 再由方程(1)有(()(())(¢()))¢+()() –(())≤ 0。对上式从1到积分有

由式(11)知式(21)的右边随→∞而趋于负无穷大, 与左边为非负数矛盾。

定理2 若

, (23)

且有式(12)、(13)成立, 则方程(1)的任意有界解振动或单调趋于0。

证明 由于条件(13)在定理1证明中仅用于情形(iii)和情形(iv), 因此先只须证这两种情况不成立。要不然, 必及1≥0, 使得当≥1时,() ≥,(()) ≥, 从而有((())) ≥() > 0。

先证定理1中的情形(iii),() > 0且¢() > 0,≥0不成立。由式(14)得式(16), 从而有, 对任意≥1均有, 因而, 得, 经积分有

由式(23)知式(24)的右边趋于无穷大, 这与左边有界矛盾。

下面来证明定理1中的情形(iv),() > 0, 且¢() < 0,≥0不成立, 类似与定理1中情形(iv)可得式(21)成立, 从而有, 因而, 经积分得

由式(23)知式(24)的右边随→∞而趋于负无穷大, 与左边为正数矛盾。

参考文献：

[1] Peng Mingshu, Ge Weigao, Huang Lihong, et al. ACorrection on the Oscillatory Behavior of Solution of Certain Secong-Order Nonlinear Differential Equations [J]. Appl Math Comput, 1999, 104: 207–215.

[2] Li Wangtong. Oscillation of Certain Second-Order Nonlinear Differential Equations [J]. J Math Anal, 1998, 217: 1–14.

[3] Li Wangtong. Positive Solutions of Second Order Nonlinear Differential Equations [J]. J Math Anal, 1998, 221: 326–337.

[4] 彭名书, 葛谓高, 王淮. 非线性泛函微分方程解的性态[J]. 应用数学学报, 2002, 25: 366–371.

[5] 白玉真. 一类二阶非线性微分方程解的振动性与渐近性[J]. 数学年刊, 2002, 23: 339–344.

(责任编校: 江河)

Oscillation for certain nonlinear second order functional differential equstions

Fan LiangJun, Zheng WenJuan

(Modern Educational Technology Center of Changde Vocational Technical College, Changde 415000, China)

Some conditions are obtained about the solution of oscillatory of a class of the second order nonlinear functional differential equations, and some results of correspondingly articles are popularized, and the application of correspondingly theorem is enlarged.

nonlinear; functional differential equation; oscillation; positive quotient

10.3969/j.issn.1672–6146.2015.02.007

O 175.12

1672–6146(2015)02–0019–04

范良君, flj5808@163.com。

2014–10–30

常德职业技术学院项目(ZY1452)。