热成形工艺中界面换热系数求解方法对比分析

常颖，唐行辉，王斌，盈亮，王存宇，赵坤民



热成形工艺中界面换热系数求解方法对比分析

常颖1，唐行辉1，王斌1，盈亮1，王存宇2，赵坤民1

(1. 大连理工大学汽车工程学院，工业装备结构分析重点实验室，辽宁大连，116024；2. 钢铁研究总院特殊钢研究所，北京，100081)

根据高强度钢热成形特点，通过圆台模具实验，分别利用热平衡法、Beck非线性估算法以及基于优化的有限元仿真法(FEM优化法)求解热成形用22MnB5钢在模具淬火下的实时界面换热系数(IHTC)，并对3种求解方法的结果和适用性进行比较和仿真验证。研究结果表明：Beck非线性估算法、热平衡法与FEM优化法3种方法求解IHTC的平均误差率分别为3.7%，7.5%和10.3%左右，Beck非线性估算法最准确；同时，得出马氏体相变的发生会对样件与模具间的IHTC有正的增益效果，压强与IHTC间存在着近似幂函数关系。

热成形；22MnB5钢；界面换热系数(IHTC)；热平衡法；Beck非线性估算法；FEM优化

高强钢热成形技术是将高强度钢板(如22MnB5)加热至均匀奥氏体化后，在高温下冲压成形并在模具内以大于27℃/S的降温速率连续冷却淬火从而获得较高强度和机械性能零部件的工艺过程。运用此技术生产的汽车零部件在车身领域得到了应用[1]。零件和模具间的界面换热系数表征了高强度钢热成形冲压淬火阶段热钢板与水冷模具间热量交换的剧烈程度，将直接决定了热钢板的降温速率和零件温度场的变化情况，进而间接影响到成形后零件的强度与硬度。故高强钢热成形过程中零件与模具间的界面换热系数的精确求取将对成形零件温度场和零件性能的预测起到至关重要的作用。界面换热系数取决于接触表面载荷、温度(模具和零件)、表面粗糙程度和材料热物理性能等诸多复杂因素[2]。针对热成形过程的界面换热系数，Merklei等[3−4]通过试验对给定压强和温差的接触界面换热系数进行了研究，并对不同间隙值的间隙传热系数进行了比较。Abdulhay等[5−6]通过实验得到U型件实冲过程中不同部位估计2~30 MPa压力范围的接触热阻，进而得出接触热阻和压强的近似指数函数关系。目前为止，用于瞬态界面换热系数主要有3种获取方法：一是基于恒定的模具温度和Biot数较小的假设，引入牛顿冷却定律，求取界面换热系数，可称为热平衡法；二是根据实验获取的模具或零件内部温度场的变化，逆向求解界面的热流密度和界面温度，从而求出界面换热系数[2−9]，即反向热传导问题处理方法(IHCP)；三是基于优化的有限元仿真法，即FEM优化法，是工业中常用的方法，可以通过优化软件指导在FEM 软件中建立好的仿真模型，通过调整IHTC，使仿真温度场与实验值逼近吻合[10−11]。上述理论方法在热成形过程的应用上主要局限有三点：

1) 由于热成形淬火过程中模面温度是实时变化的，所以牛顿冷却定律无法直接应用，需要加以改进；

2) 反向热传导处理方法大都依赖于内部点的温度采集，为了尽量减小热传导本身的延迟和滞后性，需要对温度的采集精度和位置标定提出较高的要求；

3) FEM优化法一般只能得到淬火过程中的一个有效IHTC[12]，无法表征整个淬火过程中IHTC的实时变化情况。

因此，基于上述问题，本文作者主要研究：1) 建立圆台模型，通过表面熔焊热电偶的方式直接采集的模具表面温度历程，并利用自编的以Beck非线性估计法[13]为核心的求解程序，根据模面以下测点温度反求得到的模具表面温度进行对比，探讨Beck的非线性估计法对热成形过程中换热系数估计的适用性与准确性；2) 将热平衡法、Beck非线性估算法与FEM优化法进行对比，比较三者计算IHTC的准确性，以期获取热成形工艺中最佳的IHTC求解方式；3) 分析冲压压强因素对界面换热系数的影响。

1 实验

采用的实验装置如图1(a)所示。可调压机的公称压力为400 kN，模具材质为45号模具钢，压力平衡支座的作用是保证零件表面所受压力均匀。下模具设有三根单线细丝K型热电偶，分别采集距模面中心处2，4和6 mm处温度(如图1(b)所示)，在上模表面增加了表面熔焊的热电偶，因热电偶已与模具表面熔焊，磨平处理后，可以认为采集的温度为有效模面温度。试件采用22MnB5热成形钢,切割成直径为75 mm、高为2 mm的圆柱样件，热电偶固定在板料中心附近。试件加热至900 ℃后保温约3 min，待完全均匀奥氏体化后迅速转移，上模下行并保压30 s后取出样件。热电偶采集的温度信号通过采温装置MX100实时生成数据文档，试验过程如图1(c)所示。

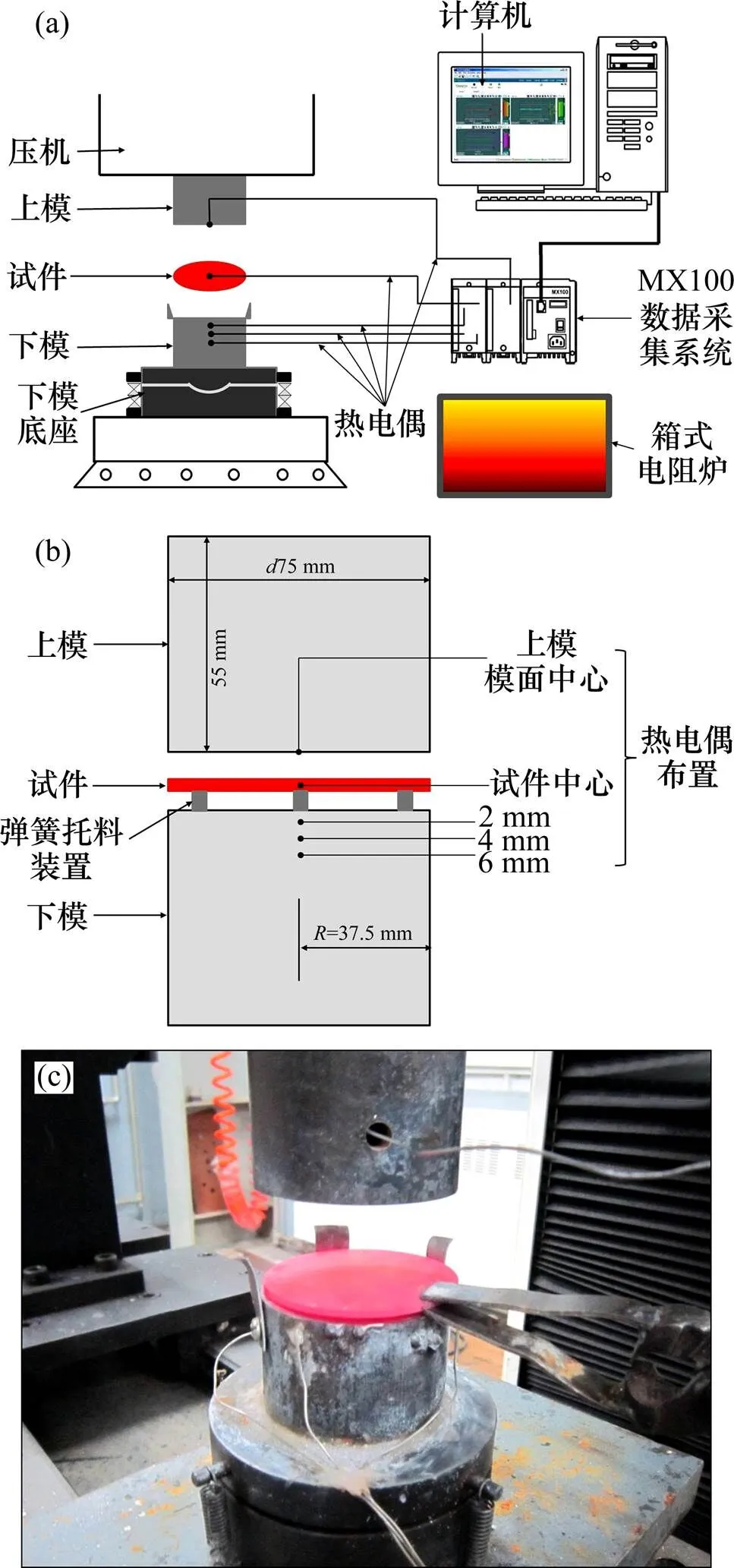
(a) 实验装置简图；(b) 热电偶布置位置下垂量测试装置示意图；(c) 实验冲压模具

2 实验结果与分析

2.1 界面换热系数的3种估算方法

在界面传热的研究过程中，系统与外界的热交换包括冲压件和模具与空气的热辐射和热对流换热,但因其量级较小,可假设系统封闭；对于试件而言，其Biot数小于0.1[14]，可采用简化的集中参数法进行分析，认为其厚度方向温度不变。基于以上假设可将实验模型可简化成一维热传导问题。

2.1.1 热平衡法

在忽略零件和模具与空气的辐射和对流换热情况下，根据能量守恒定律，零件损失的热量等于模具吸收的热量，故可推得变形后的牛顿冷却公式：

式中：为零件比热容；w为模具温度；为接触面积；为对应时刻的换热系数；(t)为时刻的板料温度，(t−1)为−1时刻的板料温度。

事实上∆时间内w是连续变化的，即使和保持不变，也难以求出微分方程的解析解。所以采用分段数值积分对连续变化的温度历程求解Δ对应的换热系数，其求解算式为

式中：eq为Δ时段的等效比热容。

22MnB5钢马氏体相变过程的eq表示为：

式中：为单位质量热焓(潜热)，J/kg；为马氏体体积分数，可根据Koistinen−Marburger定律[15]计算：

式中：s为马氏体转变温度；为相变动力因子。s和与材料相关，对于热成形过程，研究表明s还与压力相关，但针对本文的压力研究范围对应的实验观察结果，s取为400 ℃。对于普通钢材，取为0.011。求得的等效热容曲线如图2所示。

1—比热容；2—等效比热容

2.1.2 Beck非线性估计法

对于圆形板料的热冲压实验来说，不存在内热源，板料与模具间的传热问题可以近似等效为一维传热问题，故对与常物性、无内热源的一维非稳态导热问题，可表示为

式中：为导热系数；为材料密度；为材料的比定压热容；为时间；为圆台下模沿轴线方向任意位置的温度；为能量传递方向。

若给出初始时刻温度分布的初始条件(initial condition)，以及规定了边界上的热流密度，则可以对温度场进行求解，此类求解方式称为第二类边界条件求解，也称为Neumann条件求解[16]。

Beck非线性估算法处理反向热传导问题是最为经典和应用最为广泛的方法之一，其实质为一种优化方法与利用第二类边界条件求解温度场的经典组合，其优化目标函数是：

式中：为分段内计算点数量；为计算中所需测点数量。

求解思路为：给定0时刻热流密度0，求出后“1，2，…，”时刻测点温度，求出温度对热流密度的灵敏系数，修正热流密度直至满足收敛条件。通过调用Matlab中的Pdepe函数求解工具求解一维热传导偏微分方程，结合自编的迭代优化程序，求出各时段的优化收敛的热流密度。并求解出相应热流密度下不同时刻的模面温度，最后根据牛顿换热定律可得该时刻所对应的表面换热系数。如图3所示。

图3 Beck非线性估算法流程

2.1.3 FEM优化法

优化软件Isight指导在FEM软件Abaqus中建立好的仿真模型，通过给定IHTC的不断试错过程，使仿真温度场与实验值收敛吻合。分析中采用的优化方法为“Pointer”方法，优化进行时，“Pointer”方法能够自行控制步长、迭代次数等优化参数实现最高的优化效率。

误差函数为：

式(7)所示为零件温度场仿真值与实测值最小方差，式(8)所示为模具已知测点位置温度场仿真值与实测值的最小方差。

FEM优化法计算流程如图4所示。

图4 FEM优化流程

2.2 实验结果和IHTC的求解

图5所示为冲压压强1 MPa下采集的温度曲线。由图5可以看出：在极短时间内(约2.5 s)，样件温度由750 ℃降到约400 ℃(s点)，降温速率突然减缓，此时发生马氏体相变过程，释放潜热。模面温度快速上升至约150 ℃后趋于稳定而后略微上升出现拐点，同样由相变的原因来解释。

1—试件温度；2—测得模面温度；3—测得模面下2 mm处温度；4—测得模面下4 mm处温度；5—测得模面下6 mm处温度

3种方法所计算的界面换热系数曲线如图6所示。由图6可见：热平衡法与Beck估算法所得的IHTC曲线整体趋势是一致的。在样件和模具刚接触时，样件和模具逐渐进入理想的接触状态，然后随其温度下降，温差缩小，热传导的驱动力不断减小，IHTC减小。当温度降到马氏体转变温度s点(400 ℃附近)时相变发生，由此所导致的体积膨胀、相变塑性、相变表面浮凸[17]等因素综合影响下会在一定程度上增大零件与模具的实际接触面积，而相变过程中材料热物性参数的改变、潜热释放等原因也会导致热传导驱动力增大，两者综合作用下最终导致了相变对IHTC正的增益效果。FEM优化法进行对冲压压强1 MPa下模具与板料间有效IHTC的估算结果为1.728 kW/(m2·K)。

1—界面换热系数(Beck非线性估算法)；2—界面换热系数(热平衡法)；3—界面换热系数(FEM优化法)

2.3 试验结果分析

将热平衡法和Beck非线性估算法所求换热系数带入Deform 3D软件中，保证其他材料的力学参数与热物性参数均为一致，带入实验的边界条件进行瞬态热传导计算并模拟零件降温过程。

3种方法下样件淬火温度仿真值与测量值之间的收敛情况如图7(a)所示，利用Beck非线性估算法，反算求解的模具温度与实测温度吻合情况如图7(b)所示。从整体上说，Beck非线性估算法能够在一定程度上很好地反映模面温度的变化，并且样件淬火温度变化的仿真值与实测值最为贴近。

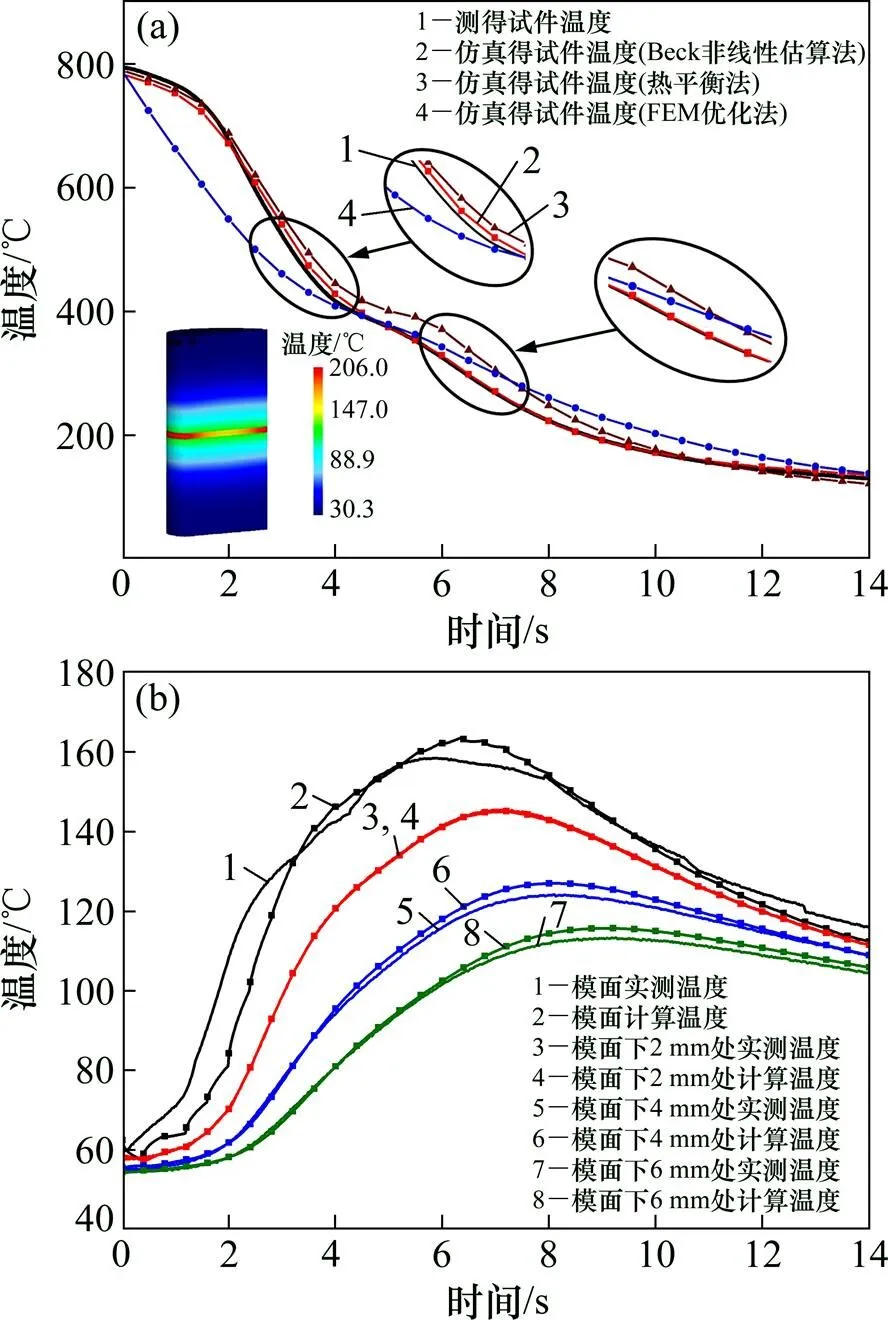
(a) 3种方法下温度仿真值与测量值之间的收敛情况；(b) Beck非线性估算法求解模温度场吻合情况

图8所示为误差分析结果。由图8可见：Beck非线性估算法能很好地反映出马氏体相变对样件和模具温度的变化情况，吻合度较好，误差控制在3.7%左右；而热平衡法虽然也能近似的得出模具与样件的实际温度变化情况，但可以看出，用等效热容来考虑相变的方式使得零件温度下降到Ms点(图8(a)中第4秒位置附近)以后，相对误差略大，总体吻合误差为7.5%左右；而FEM优化法，所求得的IHTC为1个等效值，仿真结果较前两者，与测量值吻合度误差超过了10%。

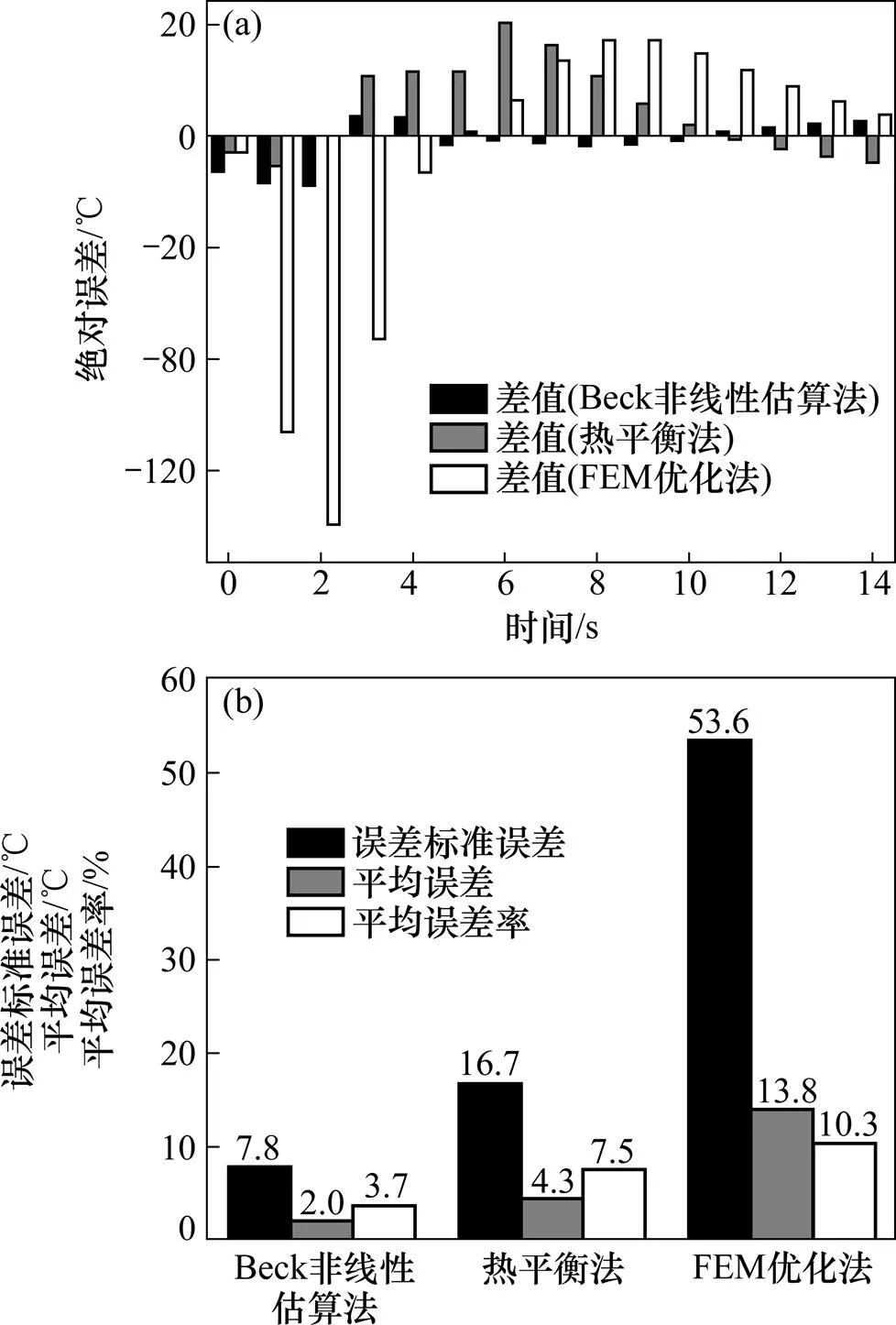
(a) 3种方法下零件淬火仿真值与真实值间的绝对误差分析；(b) 多种误差分析方法

2.4 冲压压强对界面换热系数的影响分析

冲压压强是界面换热系数的一个重要的因素。20世纪60年代，Cooper等[18−19]基于表面形貌的数学描述对接触热阻的计算和测试方法进行了研究。在不同表面进入名义上的接触状态后，其真实的接触只发生在表面凸起点上，在凸起点的间隙存在大量空气杂质，表面间的真实接触面积也仅为名义接触面积的1%~2%[20]，冲压压强越大，势必会在一定程度上会增大接触微凸体的变形，致使实际接触面积增大，接触热阻减小，界面换热系数也相应的增大。

试验中通过调节液压机冲压压力以获取不同的压强梯度，通过Beck非线性估算法得到了如图9(a)所示不同压强下样件与45号模具钢间IHTC随温度变化的实时曲线；为了更加清晰地探究IHTC与压强间的关系，将每条IHTC曲线取均值处理，得到如图9(b)所示的均值IHTC与压强之间的关系。由图9(b)可看出：均值IHTC整体上是随冲压压强的增大而增大的。经过拟合，得出IHTC与压强间存在近似的幂函数关系，按照均值IHTC与冲压压强的关系式，选用各种曲线拟合，得此关系拟合可靠度最高。

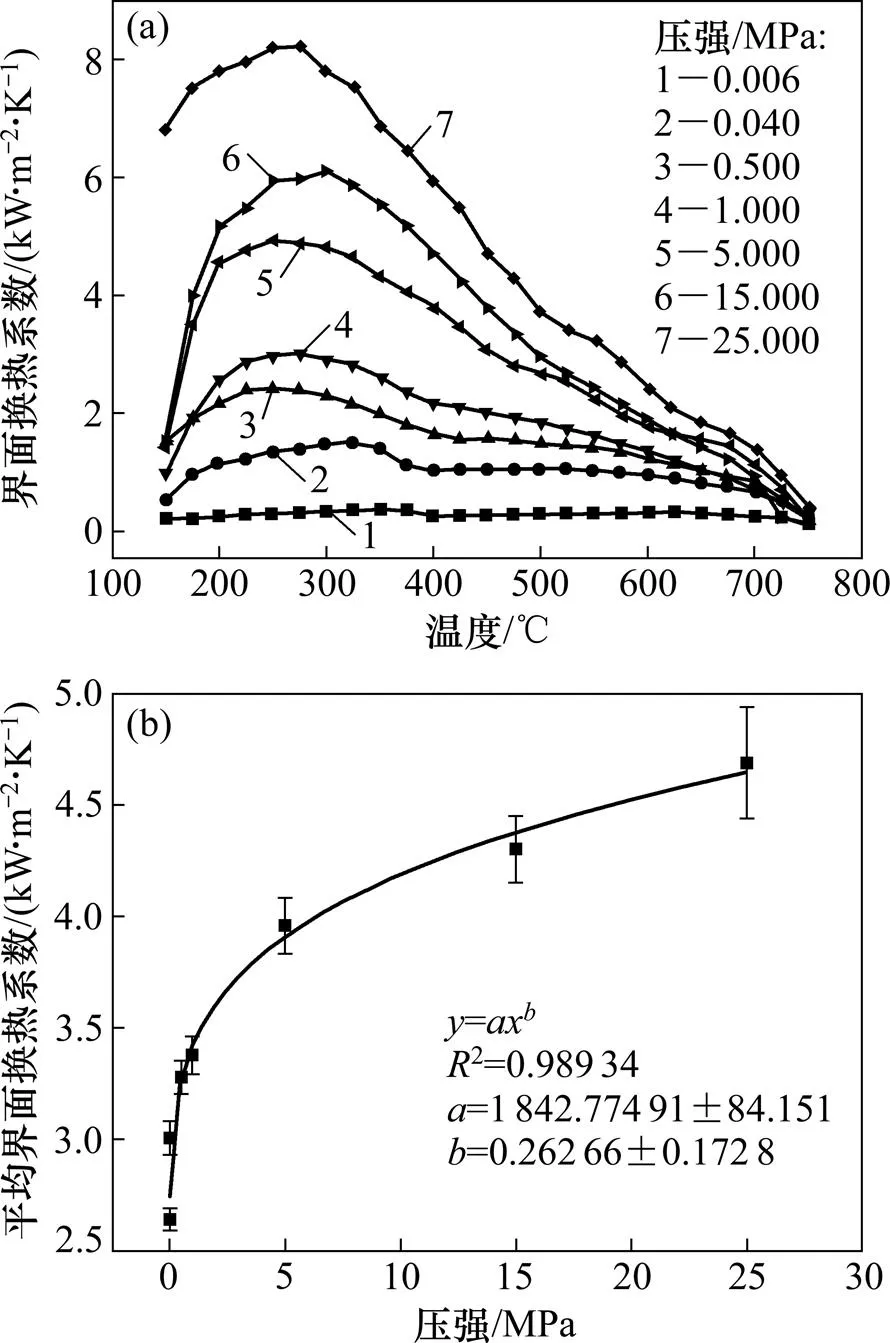
(a) 不同冲压压强下IHTC随温度变化曲线；(b) 不同压强下均值IHTC变化趋势

3 结论

1) Beck非线性估算法的求解精度最高，热平衡法求解精度次之，而FEM优化法由于所求得的IHTC为一个有效值，根据仿真结果误差最大。

2) 马氏体相变对换热会存在一定的影响，且有正向增益的效果。

3) 冲压压强是影响IHTC的重要因素，且与均值IHTC间存在近似幂函数关系。

4) 由于高强钢板热成形过程载荷较大，零件温度变化剧烈，工业中应用广泛的FEM优化法的精准度还有待进一步提高。

[1] Turetta A, Bruschi S, Ghiotti A. Investigation of 22MnB5 formability in hot stamping operations[J]. Journal of Materials Processing Technology, 2006, 177(1/2/3): 396−400.

[2] Ikeuchi K, Yanagimoto J. Valuation method for effects of hot stamping process parameters on product properties using hot forming simulator[J]. Journal of Materials Processing Technology, 2011, 211(8): 1441−1447.

[3] Merklein M, Lechler J, Stöhr T. Investigation on the thermal behavior of ultra high strength born manganese steels within hot stamping[J]. International Journal of Material Forming, 2009, 2(S1): 259−262.

[4] Bosetti P. Interlaboratory comparison for heat transfer coefficient identification in hot stamping of high strength steels[J]. International Journal of Material Forming, 2010, 3(1): 817−820.

[5] Abdulhay B, Bourouga B, Dessain C, et al. Experimental study of heat transfer in hot stamping process[J]. International Journal of Material Forming, 2009, 2(1): 255−257.

[6] Abdulhay B, Bourouga B, Dessain C. Thermal contact resistance estimation: influence of the pressure contact and the coating layer during a hot forming process[J]. International Journal of Material Forming, 2012, 5(3): 183−197.

[7] Khandelwal M, Mench M M. Direct measurement of through-plane thermal conductivity and contact resistance in fuel cell materials[J]. Journal of Power Sources, 2006, 161(2): 1106−1115.

[8] Caron E, Daun K J, Wells M A. Experimental characterization of heat transfer coefficients during hot forming die quenching of boron steel[J]. Metallurgical and Materials Transactions B, 2013, 44(2): 332−343.

[9] Bai Q, Lin J, Zhan L, et al. An efficient closed-form method for determining interfacial heat transfer coefficient in metal forming[J]. International Journal of Machine Tools and Manufacture, 2012, 56: 102−110.

[10] 郭志鹏, 熊守美, 曺尚铉, 等. 铝合金压铸过程铸件/铸型界面换热行为的研究: Ⅰ. 实验研究和界面换热系数求解[J]. 金属学报, 2007, 43(11):1149−1154. GUO Zhipeng, XIONG Shoumei, CAO Shangxuan, et al. Study on heat transfer behavior at metal/die interface in aluminum Alloy die casing process: I. Experimental study and determination of the interfacial heat transfer coefficient[J]. Acta Metallurgica Sinica, 2007, 43(11): 1149−1154.

[11] 郭志鹏, 熊守美, 曹尚铉, 等. 热传导反算模型的建立及其在求解界面热流过程中的应用[J]. 金属学报, 2007, 43(6): 607−611. GUO Zhipeng, XIONG Shoumei, CAO Shangxuan, et al. Development of an inverse heat transfer model and its application in the prediction of the interfacial heat flux[J]. Acta Metallurgica Sinica, 2007, 43(6): 607−611.

[12] Wendelstorf R, Spitzer K H, Wendelstorf J. Effect of oxide layers on spray water cooling heat transfer at high surface temperatures[J]. International Journal of Heat and Mass Transfer, 2008, 51(19/20): 4892−4901.

[13] Krishnan M, Sharma D G R. Determination of the interfacial heat transfer coefficient h in unidirectional heat flow by beck's non linear estimation procedure[J]. International Communications in Heat and Mass Transfer, 1996, 23(2): 203−214.

[14] 梁昆淼. 数学物理方程[M]. 北京: 高等教育出版社, 2002: 60−65 LIANG Kunmiao. Equations of mathematical physics[M]. Beijing: Higher Education Press, 2002: 60−65.

[15] Koistinen D P, Marburger R E. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbone alloys and plain carbon steels[J]. Acta Metallurgica, 1959, 1(7): 59−60.

[16] 杨世铭, 陶文铨. 传热学[M].北京: 高等教育出版社, 2006: 69−166. YANG Shiming, TAO Wenquan, Heat transfer theory[M]. Beijing: Higher Education Press, 2006: 69−166.

[17] 刘宗昌, 计云萍, 任慧平. 近几年马氏体相变研究的进展[J]. 热处理, 2011, 26(6): 1−8. LIU Zongchang, JI Yunping, REN Huiping. Research progress of martensite phase transformation in recent years[J]. Heat Treatment, 2011, 26(6): 1−8.

[18] Cooper M G, Mikic B B, Yovanovich M M. Thermal contact conductance[J]. International Journal of Heat and Mass Transfer, 1969, 12(3): 279−300.

[19] Yovanovich M M, Fenech H. Thermal contact conductance of nominally flat, rough surfaces in a vacuum environment[C]//Thermo Physics and Temperature Control of Spacecraft and Entry Vehicles. Monterey, California, 1966: 773−794.

[20] 赵兰萍, 徐烈, 李兆慈, 等.固体界面间接触导热的机理和应用研究[J]. 低温工程, 2000, 1(4): 29−34. ZHAO Lanping, XU Lie, LI Zhaoci, et al. Study on mechanism and application of thermal contact heat transfer between solid interfaces[J]. Cryogenics, 2000, 1(4): 29−34.

(编辑 杨幼平)

Comparison of methods for calculating interfacial heat transfer coefficient in hot forming process

CHANG Ying1, TANG Xinghui1, WANG Bin1, YING Liang1, WANG Cunyu2, ZHAO Kunmin1

1. State Key Laboratory of Structural Analysis for Industrial Equipment, School of Automotive Engineering, Dalian University of Technology, Dalian 116024, China; 2. Institute for Special Steels, Central Iron & Steel Research Institute, Beijing 100081, China

The real-time interfacial heat transfer coefficient (IHTC) of 22MnB5 steel in hot forming process was calculated by means of heat balance method, Beck’s non-linear estimation method and optimization-based finite element simulation. The results show an average error of 3.7% for Beck’s non-linear estimation method, 7.5% for heat balance method, and 10.3% for finite element simulation. The positive effect of martensitic transformation on interfacial heat transfer coefficient is obtained. Additionally, the relationship between the pressure and the heat transfer coefficient is approximated by a power function.

hot forming; 22MnB5 steel; interfacial heat transfer coefficient(IHTC); heat balance method; Beck’s non-linear estimation method; FEM optimization

10.11817/j.issn.1672-7207.2015.04.006

TG162.83

A

1672−7207(2015)04−1208−07

2014−04−13；

2014−06−20

国家自然科学基金资助项目(10932003，51101036)；辽宁省自然科学基金和教育部留学回国人员科研启动基金联合资助项目(优秀人才培育2014028001)(Projects (10932003，51101036) supported by the National Natural Science Foundation of China; Project (2014028001) supported by the Natural Science Foundation of Liaoning Province and China MOE Scientific Research Funds for Returned Overseas Scholar)

赵坤民，教授，博士生导师，从事金属热处理研究；E-mail：kmzhao@dlut.edu.cn