近场脉冲型地震动作用下设计位移反应谱

王亚楠，李慧，杜永峰, ，徐天妮



近场脉冲型地震动作用下设计位移反应谱

王亚楠1，李慧2，杜永峰1, 2，徐天妮1

(1. 兰州理工大学防震减灾研究所，甘肃兰州，730050；2. 兰州理工大学西部土木工程防灾减灾教育部工程研究中心，甘肃兰州，730050)

选取属于特定震源机制、场地平均剪切波速、震级和断层距下的36条近场脉冲型地震记录作为输入，按照速度脉冲周期对地震记录进行分组，运用Matlab进行脉冲型地震动作用下的位移反应谱计算，采用标准化和平均化的方式研究位移反应谱的特征，用分段线性拟合方法建立以速度脉冲周期作为特征周期的设计位移反应谱，给出位移反应谱的峰值和分段周期。研究结果表明：脉冲型地震动下位移反应谱的谱形呈现出4个阶段，谱特征周期近似等于速度脉冲周期，经标准化和平均化后的谱峰值约等于2.2，文中给出的设计位移反应谱能较好地拟合平均位移反应谱。

近场脉冲型地震动；位移反应谱；速度脉冲；脉冲周期

随着近场地震记录数据的不断增加以及针对近场地震动研究的逐步深入，人们对近场地震动的主要特征及其引起结构严重破坏的原因已经有了较为深刻的认识[1−5]。具有强破坏力的近场地震动大都具有明显的长周期速度和位移脉冲，使结构承受很高的能量冲击，在结构中产生较大的内力和位移，对结构提出更高的延性需求，因此关于近场地震动中所含脉冲部分的识别、模拟以及它对结构的影响引起了广泛地关注。基于位移的设计方法作为基于性能的抗震设计方法的一种，引起了广泛的关注。基于位移的设计方法地实施需要可靠的位移反应谱，由于缺少可用的设计位移谱，阻碍了该方法的推广应用。鉴于此，国内外很多学者对设计位移反应谱展开了研究。杨松涛等[6]提出了位移谱特征周期的概念，并以弹性位移谱特征周期对应的点为基准点对位移谱进行标准化，总结了此标准化方法下的平均位移谱的特征。曹加良等[7]研究了位移谱的影响因素及控制参数，建立了能供长周期结构设计使用的弹性相对位移谱。李恒等[8]通过研究位移反应谱的特性，提出了长周期段设计地震反应谱的建议形式。徐龙军等[9]给出了近断层地区岩石和土层场地上考虑方向性效应影响的设计谱，并通过与规范设计谱比较得出结论，我国设计谱的取值偏低，尚需考虑近断层脉冲型地震动的影响。卢明奇[10]选取大量的近断层地震记录作为统计样本，根据得到的平均弹性位移反应谱，给出了近断层地震设计弹性位移反应谱表达式，该表达式可以反映震源机制和场地土等因素的影响作用。谭平等[11]通过对大量近场地震记录的分析，得到了相应的弹性反应谱，并与我国规范标准反应谱进行了比较。从上述文献可以看出：针对位移反应谱的研究是随着结构的不断发展以及对地震动特征研究地不断深入而不断深入的。由于近场地震动筛选标准的不统一，各国学者多依据主观判断选取近场地震动，这必然导致在对近场地震动相关课题进行研究时，所选取地震记录的差异较大，由此得出的结论就可能存在较大差别。随着关于近场地震动特点及其破坏能力研究地不断深入，已经可以用参数化及量化指标来准确地描述近场地震动，并且可以运用这些参数和指标对近场地震动进行分类。至今为止，脉冲型地震动还没有一个准确的定义。通常情况下，提到的脉冲型地震动指的是那些包含显著加速度、速度或位移脉冲的近场地震动，脉冲的特点与它的幅值、持时以及所包含的能量相关联。人们可以通过视觉观察来简单地判断地震动中是否存在脉冲，但是这并不是一种科学的、精确的方法，因此，迫切需要一种量化的方法来减少人们主观判断所带来的不确定性。Baker[5]提出了一种能够定量地识别包含强速度脉冲的近场地震动的方法，该方法采用小波变换来识别和提取速度时程中所包含的脉冲部分。从原始地震动中提取出速度脉冲后，如果该地震动剩余部分的峰值速度以及所包含的能量与原始地震动相比变得很弱，那么该地震动可以判断为脉冲型地震动，采用指标B来度量剩余部分和原始记录的比较关系，通过对398条地震记录的分析，Baker[5]建议当B大于0.85时，该地震动属于脉冲型地震动。本文作者首先根据李明等[1]建议的方法来划分近场地震动动区域，紧接着按照Baker[5]建议的方法来选取脉冲型地震记录，然后在所选地震记录的基础上根据脉冲周期对地震记录进行分组，运用标准化和平均化的方法研究了位移反应谱的特征，最后通过分段线性拟合的方法给出了近场脉冲型地震动下的设计位移反应谱。

1 近场脉冲型地震记录选取

1.1 近场地震记录的选取准则

文中采用的地震记录均来自美国太平洋抗震研究中心(PEER)强震数据库，通过给定震级(矩震级)大小、震源机制(走滑断层、倾滑断层等)、震源距(观测点到断层破裂面的最短距离)以及场地类别(根据场地上覆30 m范围内土层的平均剪切波速确定)来选取满足需要的近场地震记录。

李明等[1]依据近场与远场存在差别的地震动特征参数，划分了近场地震动区域，并将研究结果以表格形式(表1)给出。本文根据表1提供的分类标准从PEER中筛选得到断层类型为走滑断层的近场地 震动。

表1 近场区域划分的临界断层距

1.2 脉冲型地震记录的判别方法

以选取的满足表1要求的近场地震记录作为数据库，采用Baker建议的方法[6]，按照以下步骤判断所选近场地震记录是否为脉冲型地震动：

1) 采用小波分解的方法从选取近场地震动的速度时程中提取速度脉冲部分；

2) 依据脉冲指标B判断该地震动是否属于脉冲型地震动，当B大于0.85时，该地震动被定义为脉冲型地震动。

脉冲指标B的表达式如下：

式中：PGV为剩余速度时程部分的峰值除以原始速度时程的峰值；Energy为剩余速度时程部分包含的能量除以原始速度时程包含的能量。

根据以上步骤，从PEER中选取震源机制为走滑断层、剪切波速S为180~360 m/s、震级W≥5且临界断层距满足表1要求的36条近场脉冲型地震记录，记录的相关信息见表2。

表2 近场脉冲型地震记录

2 脉冲型地震动位移反应谱

2.1 位移反应谱的建立

单自由度体系在地震作用下的运动方程为

式中：，和分别为体系的质量、阻尼系数和刚度系数；为地面运动加速度。式(2)两边同时除以，经整理得：

式中：为体系的无阻尼自振圆频率；为体系的临界阻尼比。对式(3)进行求解得到体系的相对位移反应为

式中：d为考虑阻尼时体系的自振圆频率。

依据抗震理论，在给定地震作用下有阻尼单自由度体系的最大响应(加速度、速度和位移)与体系自振周期之间的关系曲线就是反应谱。

由式(4)可知单自由度体系的最大相对位移反应D为

在建立位移反应谱时，周期的取值从0.02 s到10 s，间隔0.02 s，阻尼比取0.05，在选取的脉冲型地震动作用下进行地震响应分析，最终得到的位移反应谱如图1所示。由图1可以看出：各位移反应谱的峰值相差很大，且峰值在横坐标轴对应的周期分布范围很广，不能够反映位移反应谱的规律。

图1 未标准化位移反应谱

2.2 位移反应谱的特征研究

定量的描述位移反应谱就需要对位移反应谱的谱形、峰值以及特征周期(位移谱峰值在横坐标轴上的投影值)进行研究。

从图1可以看出：大部分地震记录的位移反应谱的谱形相似，它们均包含一个显著的峰值和4个阶段(上升段、下降段、平稳段和水平段)，个别地震记录由于频谱成分复杂而表现出2个或2个以上明显的 峰值。

以地震动的峰值位移(PG)为基准对位移反应谱的谱值进行标准化处理，得到图2所示的标准化位移反应谱(位移放大系数和结构自振周期的关系曲线，其中=D/PG)。从图2可以看出：标准化位移反应谱的峰值大部分位于1.5~2.5之间。

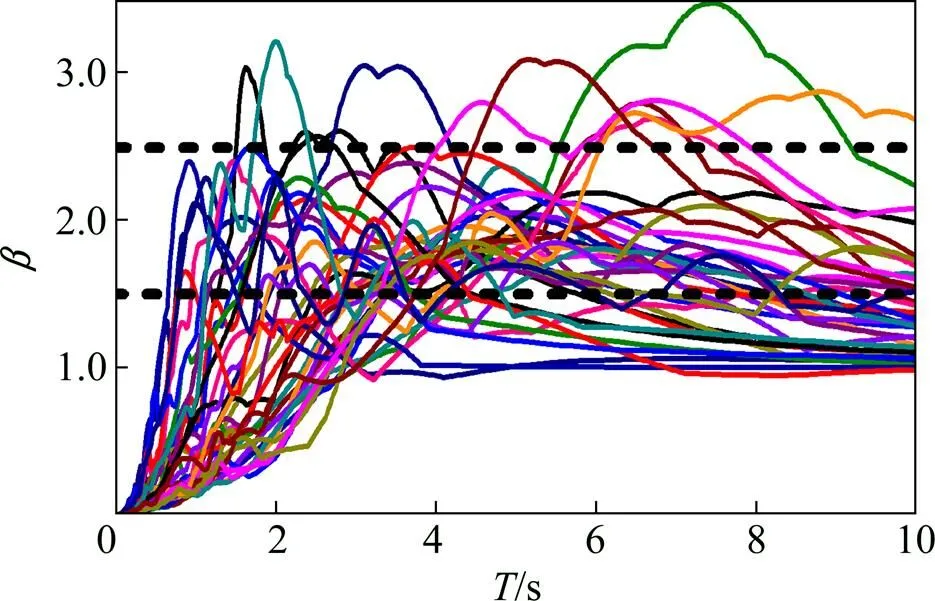
图2 标准化位移反应谱

根据地震记录脉冲周期p的分布范围将地震记录分为8组，见表3。由于实际地震记录有限，因此在某些分组中能够得到的地震记录很少。

表3 地震记录分组

图3所示为包含地震记录数量较多(≥4条)的5组标准化位移反应谱，图3中粗实线为平均后得到的平均位移反应谱。从图3可以看出：各组中标准化位移反应谱的特征周期大都集中在该分组的脉冲周期分布范围内，因此平均位移反应谱的特征周期也基本位于该分组的脉冲周期分布范围内，平均位移反应谱的峰值大致分布在2.0~2.2之间，与文献[8]得到的结论一致。

(a) GTp1；(b) GTp2；(c) GTp3；(d) GTp5；(e) GTp6

综上所述，平均位移反应谱的特征周期与地震记录的脉冲周期相对应，平均位移反应谱的峰值可近似地取为2.1。

2.3 设计位移反应谱的拟合表达式

通过前面的分析，近场脉冲型地震动作用下结构的位移反应谱的特征已经呈现出来。

根据文中得到的平均位移反应谱，采用分段线性拟合的方法得到设计位移反应谱为

式中：D为位移反应谱的谱值；PG为地震动的峰值位移；P1为位移反应谱的峰值，根据统计结果近似取为2.2；D为该峰值在横坐标轴的投影值，近似等于脉冲周期p；P2为位移反应谱下降段和平稳段交接点在纵坐标轴上的投影值，近似取为1.5；D为该交接点在横坐标轴上的投影值，根据统计结果近似等于1.5D；P3为为位移反应谱平稳段和水平段交接点在纵坐标轴上的投影值，等于1；D为该交接点在横坐标轴上的投影值，大致等于5D。根据式(6)得到的设计位移反应谱的谱形如图4所示。

图4 设计位移反应谱

图5所示为前述5组地震记录下，根据式(6)计算得到的设计位移反应谱与平均位移反应谱的对比。从图5可以看出：根据建议表达式得到的设计位移反应谱与实际地震记录的平均位移反应谱在谱形上是一致的，经历了上升段、下降段、平稳段和水平段，共4个阶段；设计谱与平均谱各阶段的分界周期吻合的较好，说明文中关于设计谱分界周期的定义较为准确；设计谱的峰值与平均谱的峰值接近。综上所述，文中给出的设计位移反应谱比较准确，可以为近场脉冲型地震动作用下结构的位移估算和基于位移的结构设计提供依据。

(a) GTp1；(b) GTp2；(c) GTp3；(d) GTp5；(e) GTp6 1—设计位移反应谱；2—平均位移反应谱

2.4 速度脉冲周期与震级之间的关系

从上述研究可以看出：速度脉冲周期p作为设计位移反应谱的重要参数，直接影响设计位移反应谱的准确性。一些学者[3−5]对脉冲型地震动的特征进行了研究，并建立了速度脉冲周期p和震级w之间的关系式，现给出3个常用的关系式：

图6所示为文中用到的脉冲型地震动记录的p与w之间的对应关系以及根据式(7)~(9)绘制的p与w间的关系曲线。由于满足文中所给条件的地震记录有限，故暂不能给出p与w之间的关系式，从数据分布总体趋势上看，式(7)和式(9)给出的关系曲线比式(8)更符合文中的情况。此外，从图6可以看出：对于这3个关系式中的任何一个，数据的离散性都比较大，因此关于脉冲周期p和地震参数之间的关系还需要进一步地研究。

1—式(7)；2—式(8)；3—式(9)；○—真实关系

3 结论

1) 位移反应谱的谱形大致由上升段、下降段、平稳段和水平段4个阶段组成。

2) 脉冲型地震动作用下位移反应谱的特征周期近似等于脉冲周期。

3) 经过标准化和平均化后位移反应谱的峰值基本为一定值，约等于2.1。

4) 已有关系式虽可以给出脉冲周期与震级之间的相关趋势，但是数据的离散性较大，还需要进一步研究。

5) 文中仅对走滑断层下、场地剪切波速为180~ 360 m/s的近场脉冲型地震动的位移反应谱进行研究，下一步将对其他震源机制、不同场地类别下的近场脉冲型地震动的位移反应谱进行研究。

[1] 李明, 谢礼立, 翟长海, 等. 近断层地震动区域的划分[J]. 地震工程与工程振动, 2009, 29(5): 20−25. LI Ming, XIE Lili, ZHAI Changhai, et al. Scope division of near-fault ground motion[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(5): 20−25.

[2] 王海云, 谢礼立. 近断层强地震动的特点[J]. 哈尔滨工业大学学报, 2006, 38(12): 2070−2076. WANG Haiyun, XIE Lili. Characteristics of near-fault strong ground motions[J]. Journal of Harbin Institute of Technology, 2006, 38(12): 2070−2076.

[3] Rupakhety R, Sigurdsson S U, Papageorgiou A S. Quantification of ground motion parameters and response spectra in the near-fault region[J]. Bull Earthquake Eng, 2011, 9: 898−930.

[4] Mukhopadhyay S, Gupta V K. Directivity pulses in near-fault ground motions-Ⅱ: Estimation of pulse parameters[J]. Soil Dynamics and Earthquake Engineering, 2013, 50: 38−52.

[5] Baker J W. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1486−1501.

[6] 杨松涛, 叶列平, 钱稼茹. 地震位移反应谱特性的研究[J]. 建筑结构, 2002, 32(5): 47−50. YANG Songtao, YE Lieping, QIAN Jiaru. Study of the displacement response spectra’s characteristics[J]. Building Structure, 2002, 32(5): 47−50.

[7] 曹加良, 施卫星, 刘文光, 等. 长周期结构相对位移反应谱研究[J]. 振动与冲击, 2011, 30(7): 63−70. CAO Jialiang, SHI Weixing, LIU Wenguang, et al. Relative displacement response spectrum of a long-period structure[J]. Journal of Vibration and Shock, 2011, 30(7): 63−70.

[8] 李恒, 李龙安, 冯谦. 用位移反应谱研究长周期设计地震反应谱[J]. 地震工程与工程振动, 2012, 32(4): 47−53. LI Hengan, LI Longan, FENG Qian. Seismic design spectra in long-period from spectral displacement analyses[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(4): 47−53.

[9] 徐龙军, 谢礼立. 近断层地区抗震设计谱研究[J]. 东南大学学报(自然科学版), 2005, 35(Sup 1): 105−108. XU Longjun, XIE Lili. Study on seismic design spectra of near-fault region[J]. Journal of Southeast University (Natural Science Edition), 2005, 35(Sup 1): 105−108.

[10] 卢明奇. 近断层地震作用下弹性位移反应谱的研究[J]. 四川大学学报(工程科学版), 2008, 40(2): 8−12. LU Mingqi. Research on elastic displacement response spectra of near-fault ground motions[J]. Journal of Sichuan University (Engineering Science Edition), 2008, 40(2): 8−12.

[11] 谭平, 谈中坤, 周福霖. 近场地震动特性及其弹性与塑性谱的研究[J]. 华南地震, 2008, 28(2): 1−9. TAN Ping, TAN Zhongkun, ZHOU Fulin. Investigation on characteristics of near-field ground motion and its elastic and inelastic response spectra[J]. South China Journal of Seismology, 2008, 28(2): 1−9.

(编辑 杨幼平)

Displacement design spectra for near-fault pulse-type ground motions

WANG Yanan1, LI Hui2, DU Yongfeng1, 2, XU Tianni1

(1. Institute of Earthquake Protection and Disaster Mitigation, Lanzhou University of Technology, Lanzhou 730050, China; 2. Western Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China)

The 36 near-fault pulse-type earthquake records that had specific fault mechanism, average shear wave velocity, magnitude and closest distance to rupture plane were used as input. The earthquake records were divided into different groups according to pulse period and the displacement response spectra under pulse-type ground motions was solved by using Matlab. The features of the displacement response spectra were studied by means of normalizing and averaging, displacement design spectra using pulse period as characteristic period was established by using piecewise linear fitting method, and the peak value and piecewise periods were provided. The results show that the displacement response spectra consist of four stages, the characteristic period is approximately equal to pulse period, the peak value of the displacement spectra getting through normalizing and averaging is about 2.2, and the displacement design spectra can fit the displacement average spectra appropriately.

near-fault pulse-type ground motions; displacement response spectra; velocity pulse; pulse period

10.11817/j.issn.1672-7207.2015.04.044

TU311.3

A

1672−7207(2015)04−1511−07

2014−04−04；

2014−06−14

国家自然科学基金资助项目(51178211)(Project (51178211) supported by the National Natural Science Foundation of China)

王亚楠，博士研究生，从事结构抗震和减震控制研究；E-mail：yananwang_xatu@163.com