磁记忆信号的量化描述

徐明秀，尤天庆，徐敏强，樊久铭，李立



磁记忆信号的量化描述

徐明秀1，尤天庆2，徐敏强3，樊久铭3，李立4

(1. 北京科技大学数理学院，北京，100083；2. 北京宇航系统工程研究所，北京，100076；3. 哈尔滨工业大学航天学院，黑龙江哈尔滨，150001；4. 齐齐哈尔大学理学院，黑龙江齐齐哈尔，161006)

采用描述材料内部磁化强度的改进的J−A理论用于分析磁记忆现象，然而磁记忆信号反映材料的表面磁场，建立这两者之间的关系。首先，设计拉伸疲劳实验研究损伤区域的磁记忆信号分布及变化特征；然后，根据实验结果建立磁偶极子模型描述材料表面散射磁场；之后，通过改进的J−A理论建立散射磁场与材料内部磁化参量0的关系，量化描述磁记忆信号。研究结果表明：条形损伤集中区域成为内部磁源，向外散射磁场；试件外某点的散射磁场由损伤集中区域的磁荷密度和尺寸、裂纹的磁荷密度、裂纹的尺寸和位置，以及该点所处的位置确定，并随磁荷密度及裂纹尺寸变化；损伤集中区域的磁荷密度与0呈线性关系，裂纹的磁荷密度与0呈线性关系、并与裂纹尺寸有关；磁偶极子模型描述的试件表面磁场的分布及分布变化特征符合实验测量结果，并可根据改进的J−A模型推得疲劳过程中磁记忆信号与应力、材料损伤情况、裂纹影响因子之间的量化关系式。

磁记忆；磁偶极子模型；散射磁场；J−A理论；疲劳损伤；量化描述

由于地磁场和循环应力的共同作用，金属材料在疲劳过程中表面磁场会发生改变，产生金属磁记忆现象[1]。利用材料表面磁信号来检测铁磁部件的应力状态和损伤情况的技术就是金属磁记忆技术。相比其他磁无损检测技术[2]，该技术不需要对被检测部件进行单独磁化，操作简单、检测成本低，因此该技术自提出以来得到学者们的广泛关注。机理研究是磁记忆技术应用的关键，近年来许多学者把J−A理论运用到磁记忆现象分析中。周俊华等[3]通过模拟材料内部的应力分布计算出有效磁场分布，从理论上解释了应力集中区磁记忆信号法向分量过零点、切向分量取极值的现象。Yang等[4−6]用等效磁场理论解释了磁记忆检测中出现的磁场反转现象。Wilson等[7−8]用接近原理解释了疲劳过程中磁信号趋于稳定的现象。Li等[9]根据J−A理论解释了旋转弯曲疲劳实验中出现的受拉和受压部位磁记忆信号数值不同的现象。参考Sablik等[10]改进J−A模型以适用于塑性变形情况，Wang等[11−12]改进J−A理论用于描述材料塑性变形和磁记忆信号之间的关系。针对疲劳载荷下的磁化特征，Xu等[13]借鉴J−A理论的思想，构造了地磁场和循环应力作用下材料磁化逐渐到达的稳定状态0，并进行了简单的试验检验。实际上，金属磁记忆技术中人们所研究的磁场其实是金属构件的外部磁场，磁记忆信号其实是物件表面的磁信号。而J−A理论及各种改进的J−A理论描述的是材料内部的磁化特性。那么，为什么这些理论描述的材料内部的磁化强度或0能解释磁记忆信号变化特征？本文作者构建磁偶极子模型找出磁记忆信号与0之间的关系，量化描述磁记忆信号。

1 拉伸疲劳试验

1.1 试验安排

根据GB/T 3075—2008“金属材料疲劳试验轴向力控制方法”，在MTS810材料试验机上进行拉伸疲劳试验。实验材料选用工程上广泛应用的Q235钢，并由静拉伸实验测得材料的屈服极限为291.3 MPa，抗拉强度为425.7 MPa。试件草图如图1所示，中间部分圆弧过渡，横截面为矩形。为了减小初始材料结构及初始磁化状态对试验结果的影响，所有试件从同一块板材上、沿同一方向切割取材，并且试验前对试验件进行了退磁处理。

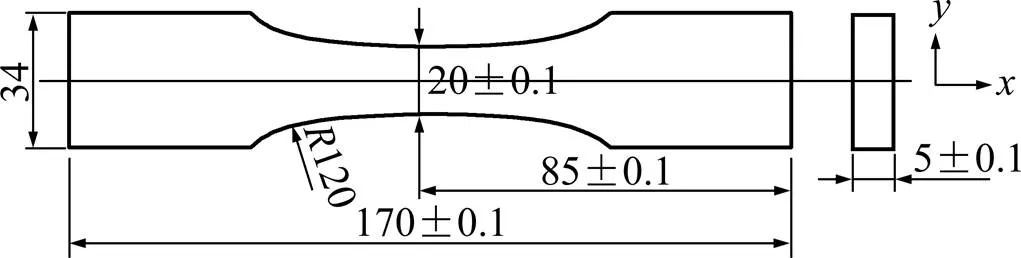
单位：mm

若干个材料和尺寸相同的试件，在相同周期性疲劳载荷下加载到不同疲劳损伤程度，然后小心卸下试件，用TSC−1M−4磁指示仪测量试件中央区域25个测量点的磁信号。测量点位置如图2所示，测量点1到25均匀分布在试件上表面，相邻点之间的间距为5 mm，1为测量点1，6，11，16和21所在直线；2为测量点5，10，15，20和25所在直线；0表示外磁场；表示轴向外力。为便于表示测量点位置，建立直角坐标系，坐标原点设在试件上表面正中央位置，轴为上表面的纵向对称轴，轴为上表面横向对称轴，轴垂直于上表面。测量磁信号时，TSC−1M−4磁指示仪探头中心距试件表面2 mm，测量点沿轴方向(切向)的磁信号记为H，沿轴方向(法向)磁信号记为H。试件所受疲劳载荷为随试件变化的正弦波周期函数，频率为5 Hz，最大应力幅为0=365.4 MPa，最小应力幅为0 MPa，应力比为无穷大。

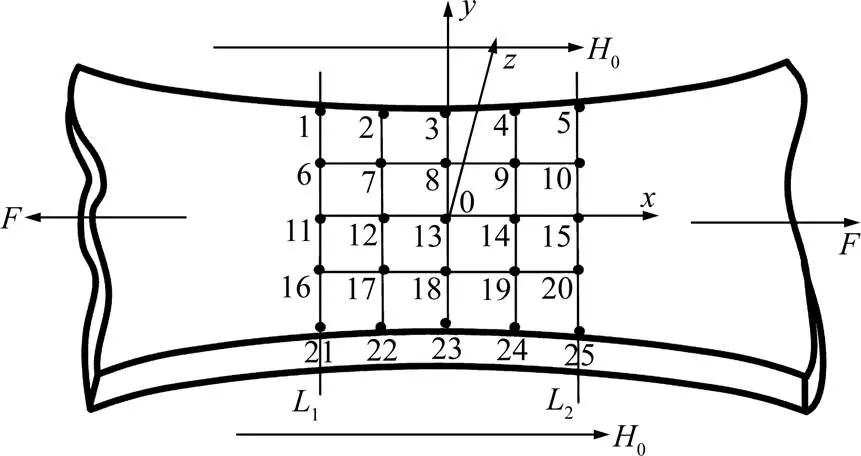
图2 试件测量位置草图

1.2 试验结果及分析

选用3个典型试件A，B和C进行结果分析。3个件的加载情况如表1所示，试件A，B和C的损伤情况依次严重；根据采集的25个测量点沿轴方向磁信号H和沿轴方向磁信号H，用Matlab画出3个件在测量区域内的H和H分布，如图3所示。下面从3个方面分析不同损伤程度的试件在测量区域表面的磁场分布特征。

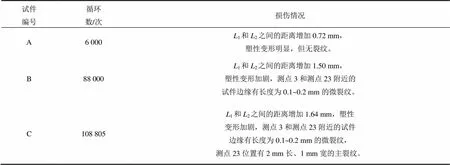
表1 试件A，B和C的加载情况

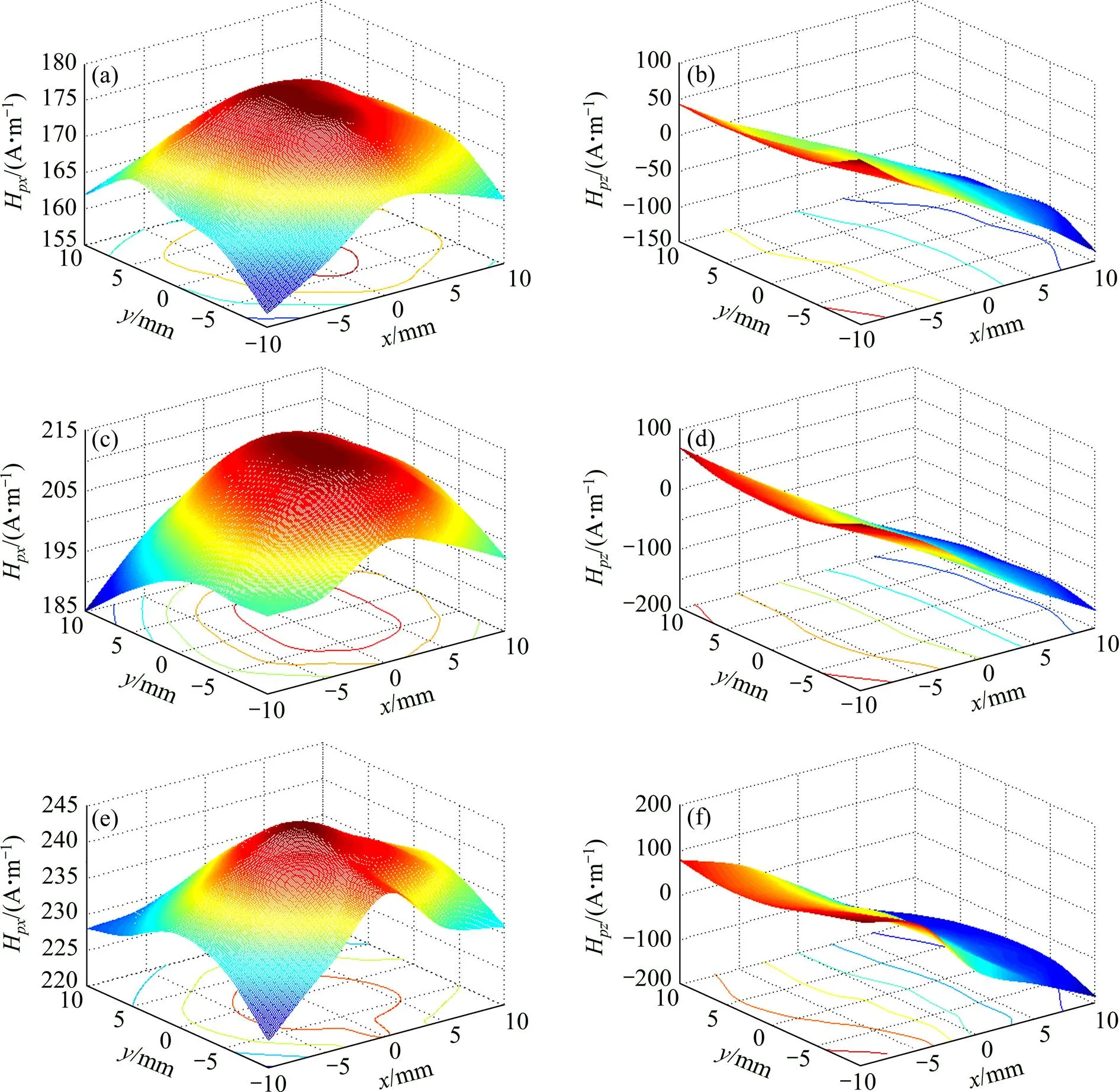
(a) 试件A，Hpx分布；(b) 试件A，Hpz分布；(c) 试件B，Hpx分布；(d) 试件B，Hpz分布；(e) 试件C，Hpx分布；(f) 试件C，Hpz分布

1.2.1 无裂纹时的磁场分布

试件A有明显塑性变形，但无裂纹，在测量区域内的磁场分布如图3(a)和(b)所示：磁信号切向分量H均为正值，呈小山包状分布，在试件中间区域有峰值；磁信号法向分量由正到负变化，呈斜坡状分布。测量区域内的磁场分布与条形磁体产生的磁场分布[14]类似。

这是随着材料塑性变形发展，测量区域内位错不断堆积，影响材料磁化而产生的。位错作为钉扎点阻碍畴壁的移动，材料磁化需要畴壁克服这些钉扎 点[15]。对于磁记忆检测中的低外磁场情况(地磁场作用下)，畴壁只能克服较弱的那部分位错钉扎点，剩余的位错钉扎点会继续阻碍畴壁运动[16]。这样，位错堆积区域材料磁化受阻，磁导率降低。从磁荷的观点来看，大量正磁荷、负磁荷分别聚集在位错堆积区域的两端，形成N极和S极。使得位错堆积区域会成为内部磁源，向外散射磁场，如图4所示。本实验中，试件中央所在的横截面面积最小、所受应力最大，关于该横截面对称的条形区域是损伤集中区域。该区域的位错堆积最严重，即可看成向外散射磁场的内部磁源。所以，试件A在测量区域的磁场分布与条形磁体产生的磁场分布类似。

图4 位错引起的散射磁场

1.2.2H峰值和H变化梯度

试件A，B和C的损伤情况依次严重，图3的磁场分布显示，3个试件的H峰值、H的最大正值和最大负值均增加。提取试件中心位置的测量点13的H和H变化梯度绝对值如表2所示，试件A，B和C在测量点13的H和H变化梯度绝对值依次增大，即损伤集中区域中心的H和H变化梯度随损伤程度的增加而增加。

表2 件A，B和C在测点13的HPx和|dHPz/dx|

既然散射磁场是由损伤集中区域内位错堆积产生，其强度就与区域内位错的数量和结构有关：位错越多，不可克服的钉扎点就越多，散射磁场就越强；位错结构越复杂，它的钉扎能力就越强，散射磁场也越强。随着材料损伤发展，位错密度增加，位错结构变复杂：由孤立位错发展为位错缠结、位错胞、滑移带、微观裂纹[17]。因此，散射磁场随着材料损伤发展而增强，其切向磁信号峰值和法向磁信号分布梯度增大。

1.2.3 裂纹对磁场分布的影响

裂纹使得裂纹位置的表面磁场分布出现畸变。试件C在测量点23附近有大裂纹，与无裂纹的试件A相比，表面磁场分布显示以下特点：H数值较大，并且在裂纹位置出现局部峰值，如图3(e)所示；H曲面沿轴向的梯度变大，最大值与最小值的幅值也变大，并且在裂纹位置出现上下波动，如图3(f)所示。

因为裂纹也会引起正、负磁荷堆积，在裂纹附近形成散射磁场。并且这个散射磁场的切向分量在裂纹位置有峰值，法向分量在裂纹中心两侧分别出现正、负峰值[18]。随着裂纹深度和宽度的增加，裂纹处散射磁场切向信号峰值变大，法向信号梯度及正负峰值变大。裂纹产生的散射磁场叠加到损伤集中区域产生的散射磁场里面，使得裂纹位置H分布出现局部峰值、H分布会出现上下波动，符合图3(e)和3(f)中的试验结果。若裂纹较小，裂纹对磁场的影响可能会被掩盖。试件B裂纹小，其表面磁场分布显示不出裂纹位置H分布有局部峰值、H分布有上下波动的特征；试件C裂纹较大，特征现象明显。

试验结果显示，对于本文研究的板状试件，裂纹在试件中央的条形区域萌生并发展。试件表面磁信号分布特征及分析也表明，在疲劳损伤集中区域形成的内部磁源大概是个条形。下面将根据这些实验特征，建立磁偶极子模型，把材料内部的磁化特性与材料表面的散射磁场联系起来。

2 磁偶极子模型

2.1 模型建立

考虑以试件中央截面(平面)为对称面的条形区域Ω为疲劳损伤集中区域，裂纹在Ω区域2个侧面萌生，如图5所示。，和分别为Ω区域的长、宽和高，界面1和2为Ω区域与试件其他区域的分界面，两侧面有任意两V型裂纹І(深为，宽为，裂纹尖端的坐标为І，裂纹边界为3和4)和П(深为，宽为，裂纹尖端的坐标为П，裂纹边界为5和6)。′和分别为Ω区域内和Ω区域外的材料磁化强度；为任意测量点。

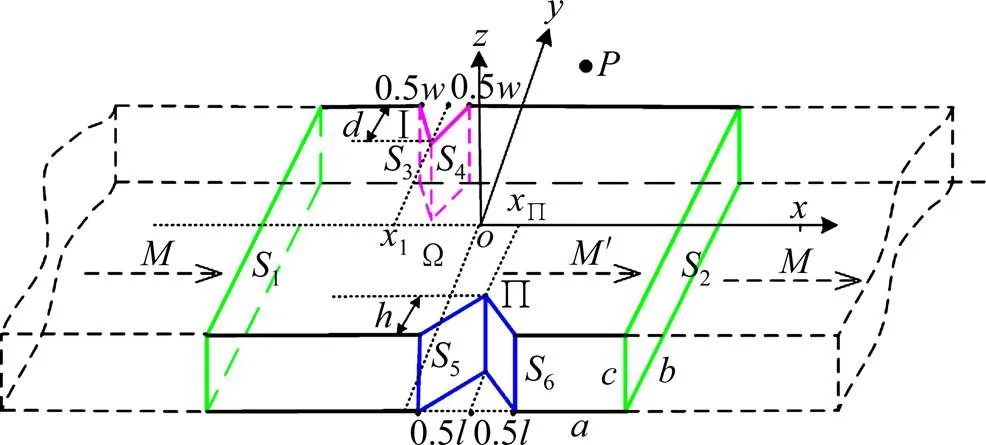
图5 Ω区域示意图

假设材料损伤只发生在Ω区域内，并且损伤是均匀的，则根据磁荷密度的定义[18]，在界面1和2上有均匀分布的磁荷，面磁荷密度分别为和−，且

裂纹І和П的边界上也会产生均匀分布的磁荷，设面磁荷密度分别为Ι和Π，表达式分别为：

把1和2界面上的磁荷等效为无数对磁偶极子，设1界面上任意面元到测量点的位置矢量为1，2界面上任意面元到点的位置矢量为2，Ω区域两边界在检测点形成的散射磁场为

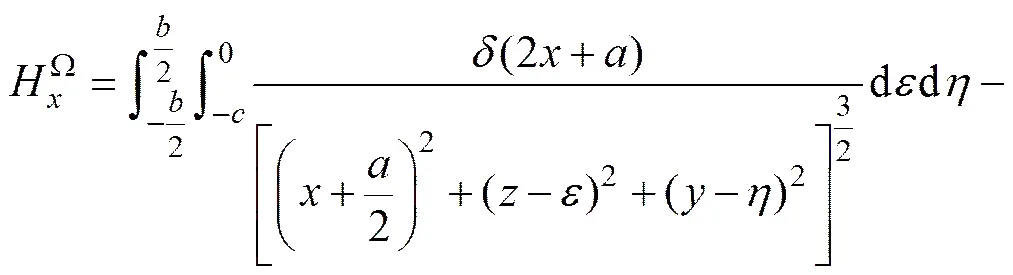
任意测量点散射磁场的由Ω区域的磁荷密度、Ω区域的尺寸()、裂纹的尺寸和位置、点位置确定。同理可求得裂纹І和П在点形成的散射磁场和以及散射磁场在和方向上的分量，和和，他们的变化由裂纹的磁荷密度、裂纹的尺寸和位置，以及点位置确定。

点总的散射磁场为Ω区域边界、裂纹边界上产生的散射磁场的总和，总的散射磁场在和方向上的分量H和H分别为：

2.2 模型分析及检验

2.2.1 散射磁场分布特征

考虑没有裂纹的情况下，取=20 mm，=20 mm，=5mm，=1，得到提离值2mm时的H和H分布，如图6所示。总体上看，区域Ω内H为正，为关于=0平面对称的曲面，呈马鞍形，有2个波峰；H是关于=0，=0轴中心对称的曲面，负半轴为正，正半轴为负。

(a) z=2 mm，Hx；(b) z=2 mm，Hz

H曲面呈马鞍型，H分布曲面翘曲严重，与图3(a)和(b)的实验结果有差别。因为实验中测量的磁记忆场P中除了散射磁场外还包括环境磁场(外磁场0与整个试件的感应磁场B之和)，如图7及式(9)所示。0可看成均匀分布，B与有相似的分布规律，但方向相反，在叠加过程中起到减弱H波峰、H曲面翘曲。此外，实际中磁荷并不是均匀分布在Ω区域的两边界，而是在界面附近及其他地方都有，只是磁荷密度以界面为中心向两边快速递减。这使得实际上H曲面不会有明显的马鞍形状，H曲面不会有严重翘曲。综合以上2个原因，考虑环境磁场的影响后，磁荷模型能描述磁记忆信号的分布特征。

p=+B+0(9)

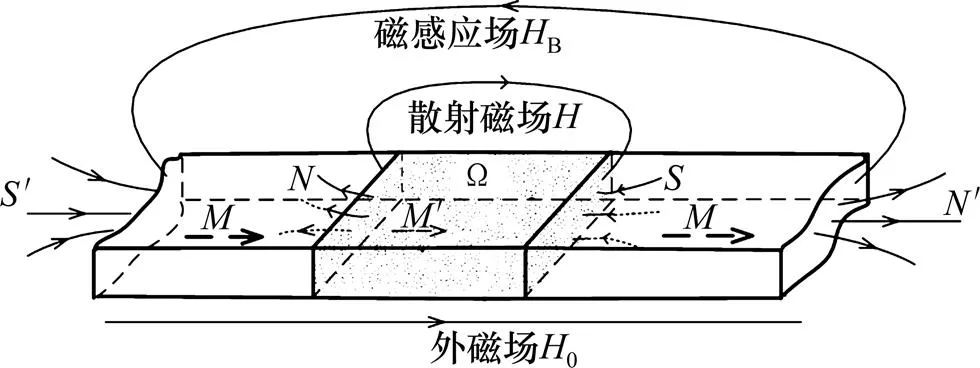
图7 考虑局部损伤的疲劳试验件的磁场示意图

2.2.2 散射磁场分布变化

根据式(7)和(8)，裂纹出现之前，测点()的散射磁场随磁荷密度变化。并且，测点()的H和H分布梯度随磁荷密度变化如下式所示：

式中：

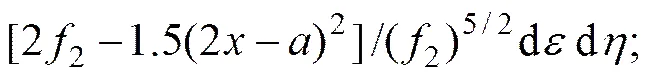
对于固定点，K和为常数；H和H分布梯度与呈比例关系；环境磁场B+0可看成常量[13]。随着疲劳损伤的发展，会增加，从而导致区域中心测点的H和H沿轴的梯度变大，符合表1所显示的实验结果。

2.2.3 裂纹对磁场分布的影响

考虑有裂纹的情况，取=20 mm，=20 mm，=5 mm，=2 mm， x=0 mm，=0.1 mm，=0.1 mm，П=0 mm，=1T，І=Π=20 T，画出总的H和H分布图像看起来和无裂纹时(图6 (a)和(b))一样。裂纹产生的散射磁场如图8所示，相比Ω区域两界面产生的散射磁场(图6(a)和(b))小大概3个数量级。仿真结果显示：较小裂纹产生的散射磁场相比Ω区域两边界产生的散射磁场弱很多，可能不会在表面磁场分布上表现出来，符合实验所显示的图3(c)和(d)的实验结果。

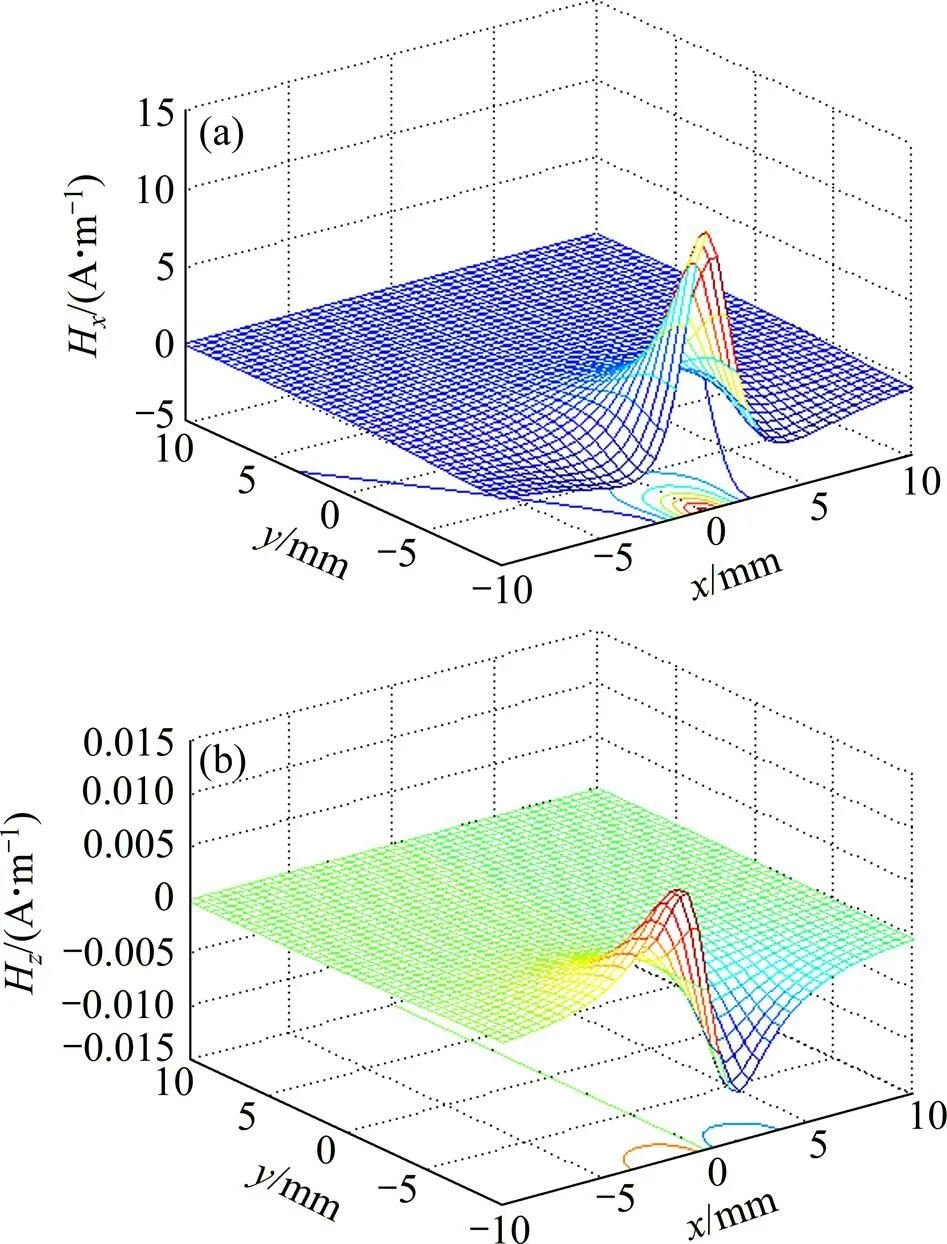
(a) z=2 mm，Hx；(b) z=2 mm，Hz

当裂纹尺寸足够大时，裂纹产生的散射磁场特征将在总散射磁场分布中体现出来，使表面磁场分布在裂纹处异常。取=20 mm，=20 mm，=5 mm，=2 mm，=2 mm，=1 mm，П=0 mm，=1T，Π=20 T时，总的H和H分布图如图9所示。在裂纹位置，H分布曲面有局部峰值，H分布曲面有上下波动，符合图3(e)和3(f)所示的试验结果。实际检测中，根据散射磁场分布的特异就可检出裂纹。

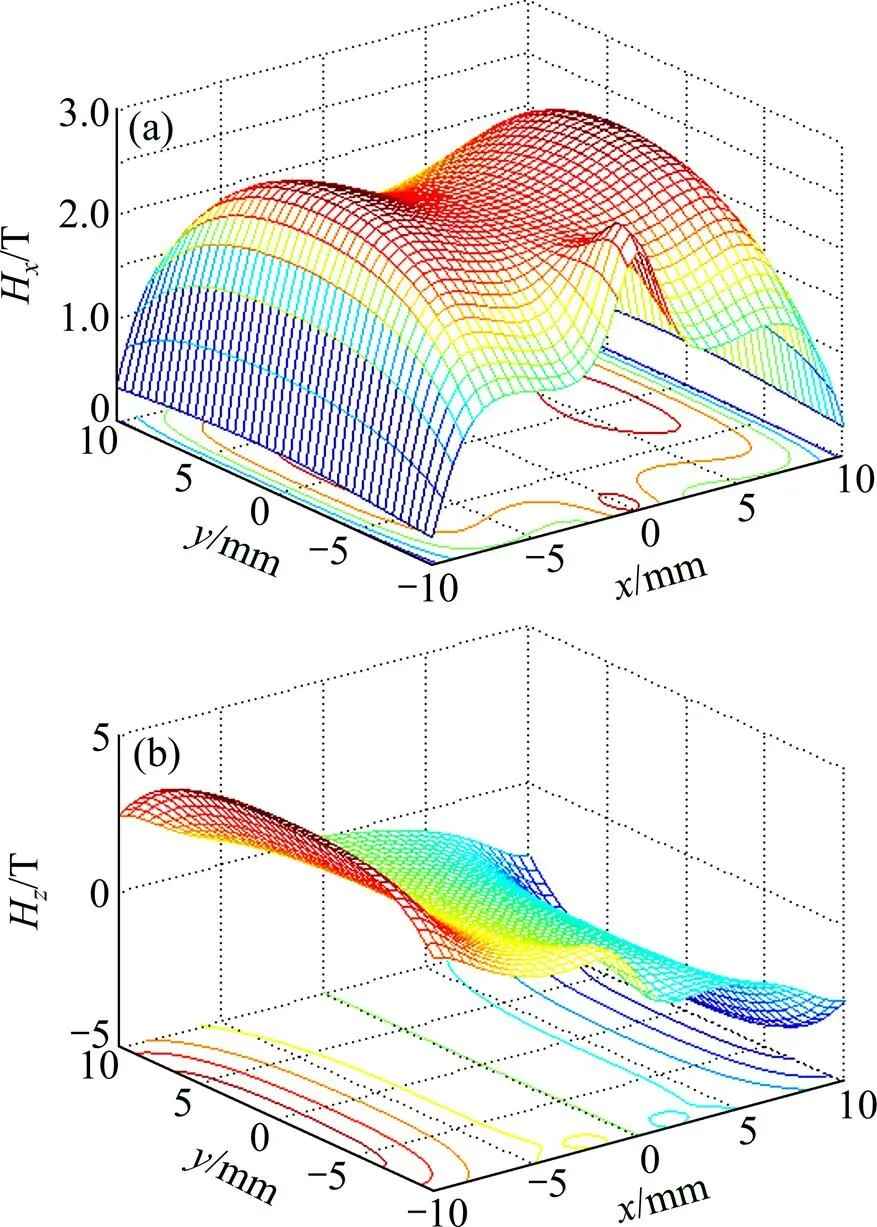
(a) z=2 mm，Hx；(b) z=2 mm，Hz

前面的磁偶极子模型虽然在建立的过程中对材料损伤情况进行了一些简化，其仿真结果也与试验测量结果有些差别，但是能反映材料损伤发展对磁信号分布的影响、裂纹对磁信号分布的影响。最重要的是，它能把材料外部的磁记忆信号与反映材料磁化特性的参量0联系起来。

3 讨论

3.1 磁荷密度表达

根据改进的J−A模型[19]，疲劳载荷作用下，材料磁化稳定于局部平衡状态0，并且0表达式为

式中：1为畴壁钉扎参数，表示畴壁对磁化的阻碍作用；为符号参数，de/d＞0时=1，de/d＜0时=−1，表明畴壁受到的钉扎作用总是阻碍磁化强度的变化。an表示非滞后磁化状态，它的表达式为[20]

式中：S为材料的饱和磁化强度；为代表有效畴密度的参数，由实验获得e为有效磁场，对于只受轴向应力的各向同性材料，其表达式为

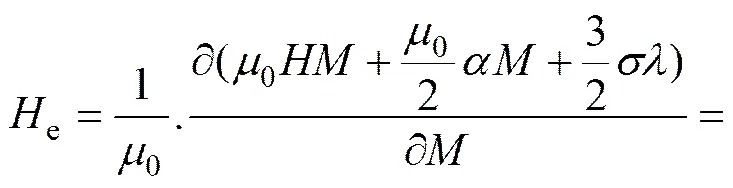
式中：为磁化耦合系数；为应力；0为真空磁导率；为磁致伸缩系数，，。

an为理想无钉扎的情况，它与0之间存在如下的能量关系：

假设材料损伤只发生在Ω区域内，并且损伤是均匀的，则所有不可克服的钉扎都均匀分布在Ω区域,区域外无不可克服的钉扎。那么，磁化稳定后，Ω区域外磁化强度就可认为是an，Ω区域内的磁化强度′为an与不可克服的钉扎产生的等效磁化强度之和。因此，

钉扎因素都考虑到0里面。

所以，Ω边界及两裂纹边界的磁荷密度分别为：

(20)

式(19)~(21)显示：Ω边界的磁荷密度与0呈线性关系，裂纹边界的磁荷密度与0呈线性关系，并与该裂纹的尺寸有关。疲劳过程中，而0以及裂纹尺寸随材料损伤发展而变化，致使Ω边界的磁荷密度、裂纹边界的磁荷密度随0变化。

3.2 磁记忆信号表达

把磁荷密度表达式(19)代入式(4)，并把磁场单位由T转换为A/m，得到Ω区域边界在点产生的散射磁场表达式为：

散射磁场与磁记忆场H存在式(9)所示关系，对于研究的固定点，把外磁场和磁感应场之和B+0看成常量，则

H=H−(26)

将式(25)和(26)代入式(12)，得到表面磁记忆信号的量化表达式：

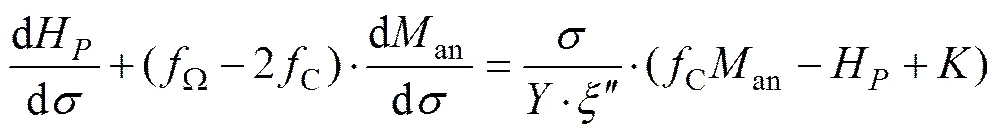
式中：H，，和为切向分量，也可为法向分量或其他方向分量。对于无裂纹的情况，。和由循环应力状态和多个材料参数确定，表达式见式(13)和(14)。和为定常参数，由载荷情况、材料特性和试件形状决定，由大量试验数据获得。式(12)中″表征材料损伤情况，由材料特性及微观结构决定。

因此，疲劳过程中H随应力的变化规律、与材料损伤之间的关系就可以通过式(27)量化表示出来了。虽然确定式(27)中的所有参数是件不容易的事，但是该式所描述的应力、损伤情况、材料特性、加载情况、磁场环境等对磁记忆信号的影响却是全面的。

4 结论

1) 板状试件拉伸疲劳后，损伤集中区域表面的切向磁信号分布呈小山坡形，法向磁信号分布呈斜坡形，类似条形磁体产生的磁场分布；切向磁信号峰值、法向磁信号的分布梯度随材料损伤发展而变大；裂纹明显时，在裂纹位置，切向磁信号分布有局部峰值，法向磁信号分布上下波动。

2) 损伤集中区域内位错堆积，成为内部磁源，向外散射磁场。建立磁偶极子模型描述散射磁场，其仿真结果在考虑环境磁场的影响后，与实验结果基本符合。

3) 材料表面某点的散射磁场由损伤集中区域的磁荷密度、裂纹的磁荷密度、损伤集中区域的尺寸、裂纹的尺寸和位置，以及该点所处的位置确定，并随损伤集中区域的磁荷密度、裂纹的磁荷密度及裂纹尺寸变化。

4) 损伤集中区域的磁荷密度与改进的J-A模型中的0呈线性增加关系，裂纹的磁荷密度与0呈线性关系、并与裂纹尺寸有关。

5) 根据磁偶极子模型反映的散射磁场与改进的J−A模型中0关系，推得疲劳过程中磁记忆信号与应力、材料损伤情况、裂纹影响因子之间的量化关系式。

[1] Dubov A A. Diagnostics of boiler tubes using the metal magnetic memory[M]. Moscow: Energoatomizdat, 1995: 1−10.

[2] 邢海燕, 徐敏强, 李建伟. 磁记忆检测技术及工程应用[M]. 北京: 中国石化出版社, 2011: 1−10.XING Haiyan, XU Minqiang, LI Jianwei. Magnetic memory testing technology and its engineering application[M]. Beijing: China Petrochemical Press, 2011: 1−10.

[3] 周俊华, 雷银照. 正磁致伸缩铁磁材料磁记忆现象的理论探讨[J]. 郑州大学学报(工学版), 2003, 24(3): 101−105.ZHOU Junhua, LEI Yinzhao. The theoretical discussion on magnetic memory phenomenon about positive magnetostriction ferromagnetism materials[J]. Journal of Zhengzhou University (Engineering Science), 2003, 24(3): 101−105.

[4] YANG En, LI Luming, CHEN Xing. Magnetic field aberration induced by cycle stress[J]. Journal of Magnetism and Magnetic Materials, 2007, 312(1): 72−77.

[5] DONG Lihong, XU Binshi, DONG Shiyun, et al. Stress dependence of the spontaneous stray field signals of ferromagnetic steel[J]. NDT&E International, 2009, 42(4): 323−327.

[6] 任尚坤, 周莉, 付任珍. 铁磁试件应力磁化过程中的磁化反转效应[J]. 钢铁研究学报, 2010, 22(12): 48−52.REN Shangkun, ZHOU Li, FU Renzhen. Magnetizing reversion effect of ferromagnetic specimens in process of stress- magnetizing[J]. Journal of Iron and Steel Research, 2010, 22(12): 48−52.

[7] Wilson J W, TIAN Guiyun, Barrans S. Residual magnetic field sensing for stress measurement[J]. Sensors and Actuators A, 2007, 135(2): 381−387.

[8] LENG Jiancheng, XU Minqiang, XU Mingxiu, et al. Magnetic field variation induced by cyclic bending stress[J]. NDT&E International, 2009, 42(5): 410−414.

[9] LI Jianwei, XU Minqiang, XU Mingxiu, et al. Investigation of the variation in magnetic field induced by cyclic tensile-compressive stress[J]. Insight, 2011, 53(9): 487−489, 493.

[10] Sablik M J, Wilhelmus J G., Smith K., et al. Modeling of plastic deformation effects in ferromagnetic thin films[J]. IEEE Transactions on Magnetics, 2010, 46(2): 491−494.

[11] WANG Zhengdao, DENG Bo, YAO Kai. Physical model of plastic deformation on magnetization in ferromagnetic material[J]. Journal of Applied Physics, 2011, 109(8): 083928.

[12] LI Jianwei, XU Minqiang. Modified Jiles-Atherton-Sablik model for asymmetry in magnetomechanical effect under tensile and compressive stress[J]. Journal of Applied Physics, 2011, 110(6): 063918.

[13] XU Mingxiu, XU Minqiang, LI Jianwei, et al. Metal magnetic memory field characterization at early fatigue damage based on modified J-A model[J]. Journal of Central South University of Technology (English Edition), 2012, 19(6): 1488−1496.

[14] 徐明秀, 徐敏强. 旋转弯曲疲劳件的法向磁信号分布[J]. 无损检测, 2009, 31(8): 606−609, 642.XU Mingxiu, XU Minqiang. Normal magnetic signals distribution analysis of rotating bending fatigue specimen[J]. Nondestructive Testing, 2009, 31(8): 606−609, 642.

[15] 冯端. 金属物理学(第四卷): 超导电性和磁性[M]. 北京: 科学出版社, 1998: 95−113, 545−560.FENG Duan. Metal Physics (Book Four): Superconductivity and magnetism[M]. Beijing: Science Press, 1998: 95−113, 545−560.

[16] 苑德福, 马兴隆. 磁性物理学[M]. 成都: 电子科技大学出版社, 1994: 286−300, 389−438.YUAN Defu, MA Xinglong. Magnetism physics[M]. Chengdu: University of Electronic Science & Technology Press, 1994: 286−300, 389−438.

[17] Subra S. Fatigue of materials[M]. Cambridge: Cambridge University Press, 2003: 27−29.

[18] 徐章遂, 徐英, 王建斌, 等. 裂纹漏磁定量检测原理与应用[M]. 北京: 国防工业出版社, 2005: 21−36.XU Zhangsui, XU Yin, WANG Jianbin, et al. The principle and application of crack leakage magnetic quantitative test[M]. Beijing: National Defence Industry Press, 2005: 21−36.

[19] XU Mingxiu, XU Minqiang, LI Jianwei, et al. Discuss on using Jiles-Atherton theory for charactering magnetic memory effect[J]. Journal of Applied Physics, 2012, 112(9): 093902.

[20] Jiles D C. Theory of the magnetomechanical effect[J]. Journal of Physics D-Applied Physics, 1995, 28(8): 1537−1546.

(编辑 杨幼平)

Quantitative representation of magnetic memory signal

XU Mingxiu1, YOU Tianqing2, XU Minqiang3, FAN Jiuming3, LI Li4

(1. School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China; 2. Beijing Institute of Astronautics System Engineering, Beijing 100076, China; 3. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 4. Department of Mathematics, Qiqihar University, Qiqihar 161006, China)

The modified J−A model that describes the magnetization intensity inside the material was used in the metal magnetic memory (MMM) phenomenon analysis. However, the MMM signal reflected the magnetic field outside the material. The relationship between the magnetization intensity and the MMM signal outside the material was established. First, the tensile fatigue test was conducted to study the distribution and variation characters of the MMM signal outside the damage area. Then, according to the experimental results, a magnetic dipole model was constructed to describe the scattering magnetic field. After that, the scattering magnetic field was related to the magnetization parameter0in the modified J−A model, and the MMM signal was described quantitatively. The research results show that the bar-type damage concentration area becomes the interior magnetic source and scatter magnetic field outside; that the scattering magnetic field at a certain point outside the specimen is decided by the magnetic charge density and size of damage concentration area, the magnetic charge density of crack, the size and location of crack, and the location of this point; and that the scattering magnetic field varies with the magnetic charge density of damage concentration area, the magnetic charge density of crack, and the size of crack. The magnetic charge density of damage concentration area has a linear increase relation with0, and the magnetic charge density of crack has a linear relation with0and relates with crack size. The distribution and distribution variation characters of magnetic field described by the magnetic dipole model are in accordance with the experimental results. And the quantitatively relational expression among the MMM signal, stress, material damage situation and crack impact factor is obtained based on the magnetic dipole model and the modified J−A model.

magnetic memory; magnetic charge model; scattering magnetic field; J−A theory; fatigue damage; quantitative representation

10.11817/j.issn.1672-7207.2015.04.007

O346.2；O441.2

A

1672−7207(2015)04−1215−09

2014−04−13；

2014−06−20

中央高校基本科研业务费专项资金资助项目(FRF-TP-14-067A2)；国家自然科学基金资助项目(10772061)；黑龙江省自然科学基金资助项目(A201210)(Project (FRF-TP-14-067A2) supported by the Fundamental Research Funds for the Central Universities; Project (10772061) supported by the National Natural Science Foundation of China; Project (A201210) supported by the Natural Science Foundation of Heilongjiang Province of China)

徐明秀，博士，讲师；从事疲劳损伤检测研究；E-mail：xmxyippee@126.com