温度梯度作用下纵连板式无砟轨道疲劳应力谱

徐庆元，孟亚军，李斌，娄平，闫斌



温度梯度作用下纵连板式无砟轨道疲劳应力谱

徐庆元，孟亚军，李斌，娄平，闫斌

(中南大学 土木工程学院，湖南 长沙，410075)

为了研究服役期间温度梯度作用下纵连板式无砟轨道疲劳应力谱，建立基于传热学理论的纵连板式无砟轨道温度梯度计算模型和温度梯度作用下疲劳应力谱计算模型，并对模型进行验证。以广州气象数据为例，首先利用经过验证的温度梯度计算模型计算服役期间轨道板温度梯度时程曲线，然后将所计算的温度梯度时程曲线输入经过验证的疲劳应力谱计算模型，得到服役期间自重和温度梯度时程曲线作用下不同板厚和裂缝间距的纵连板式无砟轨道疲劳应力谱。研究结果表明：服役期间温度梯度作用下纵连板式无砟轨道疲劳应力谱具有明显的时变特性；板厚对温度梯度作用下服役期间纵连板式无砟轨道疲劳应力谱影响较小，裂缝间距对其影响很大。

轨道工程；传热学；温度梯度；纵连板式无砟轨道；疲劳应力谱

轨道板为钢筋混凝土结构，热传导性能较差，在随时间变化的气温和太阳辐射作用下，轨道板表面温度迅速上升或下降，但内部温度变化缓慢，会在轨道板厚度方向形成具有时变特性的温度梯度，且已有研究表明，温度梯度的变化与气温变化不同步，变化具有滞后性[1]。当轨道板在温度梯度作用下的变形受到约束时，会产生可接近甚至超过列车荷载应力的温度应力。目前，众多学者对温度梯度作用下无砟轨道温度应力进行了研究，取得了大量研究成果，如赵坪 锐[2]对最大温度梯度作用下轨道板的翘曲应力进行了研究；石现峰等[3−7]对不同正负温度梯度作用下轨道板温度应力进行了计算。但这些研究中温度梯度均取为定值，未考虑温度梯度的时变特性。文献[8]对道床板混凝土温度梯度应力进行了研究，但研究时假设温度梯度应力时程与气温变化同步，未考虑温度梯度变化的滞后性。在此，本文作者借鉴国内外研究成果，基于传热学理论建立考虑温度梯度时变特性和变化滞后性的服役期间纵连板式无砟轨道温度梯度及温度梯度作用下疲劳应力谱计算模型，并对模型进行验证。利用验证的模型计算服役期间不同板厚温度梯度时程曲线，并基于温度梯度时程曲线计算结果对服役期间不同板厚和裂缝间距的纵连板式无砟轨道疲劳应力谱进行研究，以期为服役期间纵连板式无砟轨道疲劳理论研究提供参考。

1 温度梯度计算模型

1.1 传热方程

热能传递包括热传导、热对流和热辐射3种方 式[9]， 外界气温、辐射等通过轨道板板顶逐步向板内传热。研究表明，水泥混凝土板顶中心与板边温度一般没有差别[10−11]，轨道板面各点对应的上下表面温差较接近[7]。因此，可假定轨道板在平面上温度均匀分布，温度只沿厚度方向变化，将轨道板在服役期间气候条件下的传热化为一维热传导问题，微分方程为：

式中：为温度；为时间；为从板顶算起的深度；为导温系数，；为导热系数；为比热容；为混凝土的容重。

1.2 边界条件

轨道板直接暴露在气候条件下，其温度分布主要受气温、太阳辐射及其有效辐射影响。借鉴国内外研究成果[10−15]，将自然气候条件下轨道板边界温度化为第三类边界条件，板顶热平衡方程为：

式中：T为考虑有效辐射后的气温；为板顶对太阳辐射的吸收系数；Q为太阳辐射；T和Q为时间的函数；为综合表面传热系数[12]。()为风速函数；Δ为轨道板表面和空气之间的温差。采用日平均风速代替风速函数计算表面传热系数误差很小[13]，因此，本文采用日平均风速。

气温的日变化过程用2个正弦波模拟，有效辐射的计算与实测较困难，一般采用扩大气温振幅的方 法[14]或采用三角函数的线性组合进行拟合[15]，但后一种方法的系数需要多年统计数据才能达到一定的精度。本文采用扩大气温振幅的办法近似考虑有效辐射。则考虑有效辐射后T的表达式为：

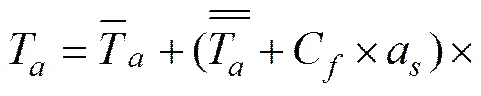
太阳总辐射的日变化过程用分段函数近似拟 合[10, 14]，微分运算后用傅里叶级数展开：

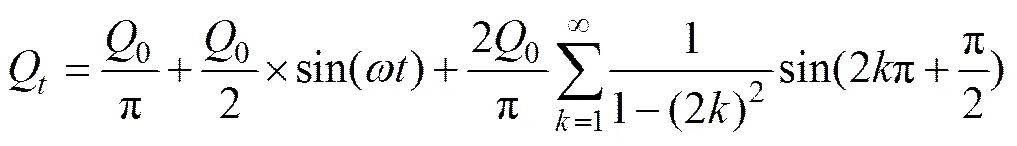
式中：Q为太阳辐射；0=0.131Q；Q为总辐射日总量；，为实际日照时间，h。计算表明：傅里叶级数取10~20项时，转换为气温后，温度精度可达到0.01 ℃，本文取20项。

1.3 模型验证

为验证本文温度梯度计算模型的正确性，从气象局获得2010年广州气象资料，运用建立的模型计算了轨道板板厚为200 mm时的温度梯度时程曲线。热工参数见表1，广州2010年温度梯度时程曲线见图1，2010−07−01—02温度梯度与考虑气温、太阳辐射和有效辐射的板顶换算温度时程曲线放大图见图2，温度梯度时程曲线最大值对比见表2。

表1 热工参数

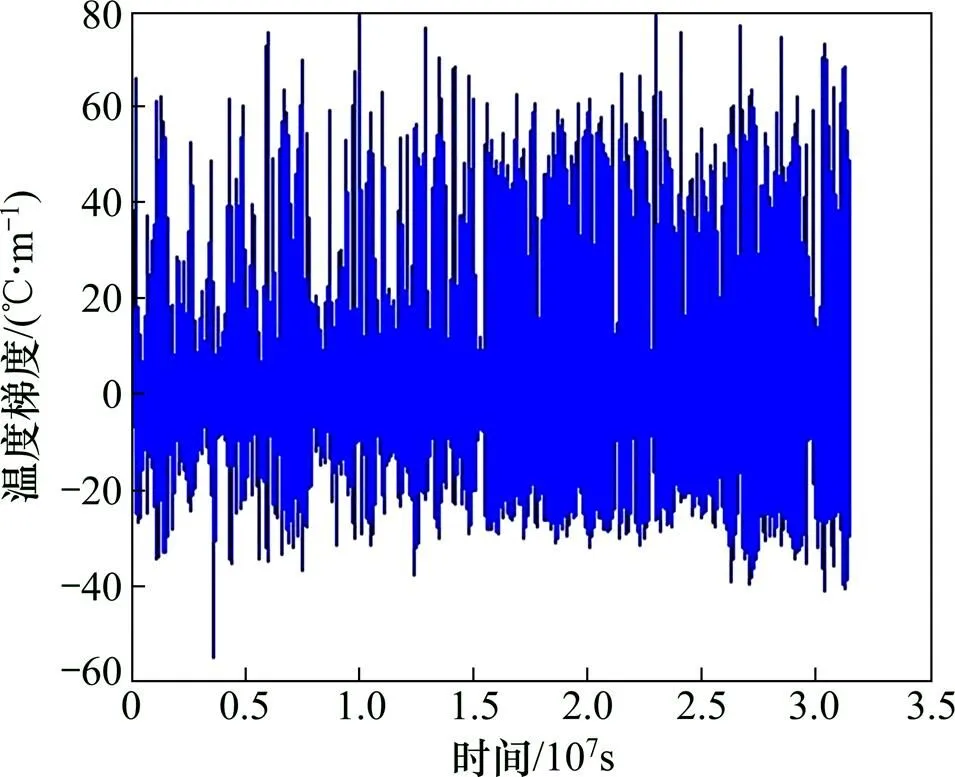
图1 温度梯度时程曲线

1—温度梯度；2—板顶换算温度

表2 温度梯度计算结果比较

图2表明，本文模型计算的温度梯度时程曲线日变化规律符合文献[1]规律，温度梯度的变化滞后于板顶换算温度变化，能考虑温度梯度变化的滞后性。表2表明，温度梯度时程曲线最大值与文献[2]和规范建议值很接近。文献[2]和规范中提出的是多年数据统计后的温度梯度最大值，而本文仅计算了2010年温度梯度时程曲线，因此，本文温度梯度时程曲线最大值略偏小。

2 应力谱计算模型

2.1 模型建立

路基上纵连板式无砟轨道疲劳应力谱计算模型如图3所示。模型中，轨道板、底座板用实体单元模拟，轨道板与底座板间连接、底座板与路基间连接用接触单元模拟，可考虑服役期间自重和温度梯度时程曲线作用下轨道板和CA砂浆之间可能存在的脱空对服役期间无砟轨道疲劳应力谱的影响。路基上纵连板式无砟轨道钢筋在纵向是连续配置的，但无砟轨道混凝土是按开裂设计考虑的。为了考虑无砟轨道开裂的影响，轨道板之间、底座板之间设置刚度为无砟轨道混凝土开裂后裂缝处刚度的纵向连接单元。

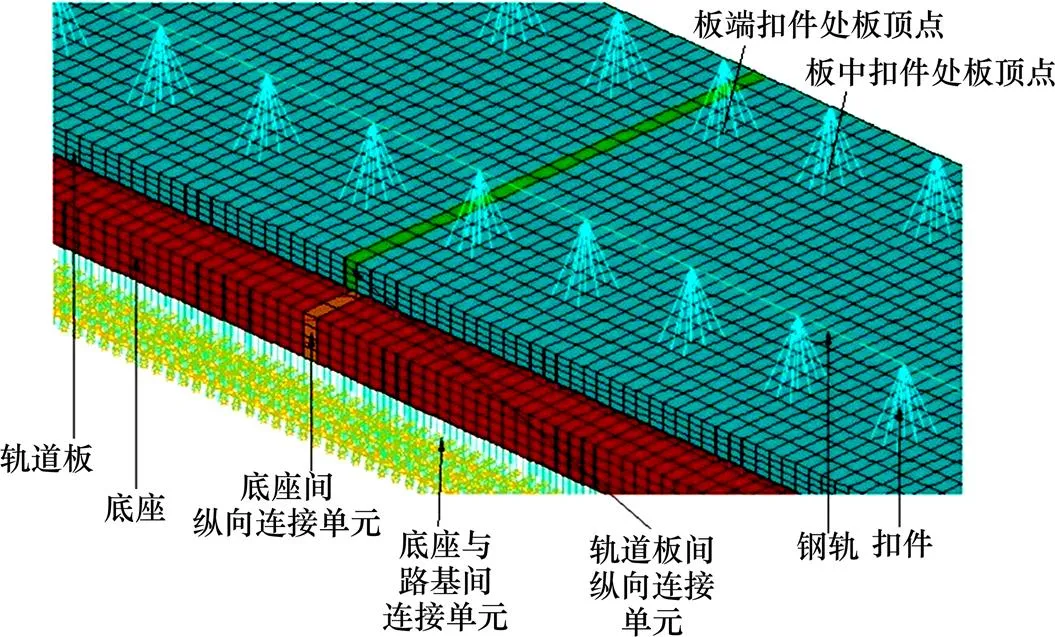
图3 路基上纵连板式无砟轨道疲劳应力谱计算模型

2.2 模型验证

文献[2]对自重和18.468 ℃温度梯度作用下路基上I型板式无砟轨道轨道板翘曲应力和翘曲变形进行了计算，为了验证本文自重和温度梯度作用下无砟轨道应力计算的正确性，进行了相同工况下轨道板翘曲应力和变形计算，计算结果对比见表3。

从表3可以看出：本文计算结果与文献[2]结果很接近，验证了本文所建模型计算服役期间自重和温度梯度作用下无砟轨道应力的准确性。

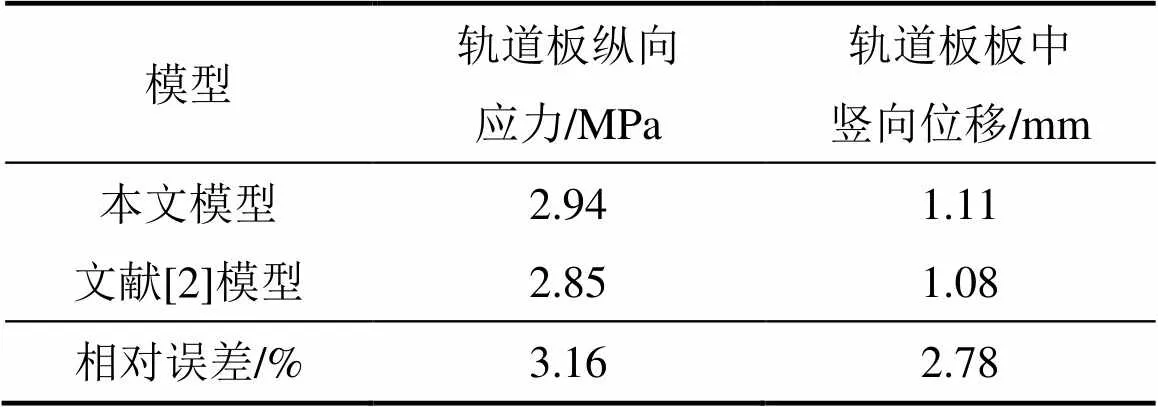
表3 计算结果比较

3 算例分析

3.1 计算条件

基于广州气象资料，计算服役期间温度梯度时程曲线及在温度梯度时程曲线和自重荷载作用下服役期间轨道板疲劳应力谱。裂缝间距取1.95 m(3个扣件间距)和2.6 m(4个扣件间距)，轨道板厚度取190 mm，200 mm和210 mm。无砟轨道计算参数见表4，计算工况见表5。

表4 无砟轨道计算参数

3.2 计算结果

根据板厚为200 mm时，2010年温度梯度时程曲线(见图1)，不同板厚下温度梯度时程曲线最值如表6所示。工况2板端扣件处板顶点、板端扣件处板底点、板中扣件处板顶点和板中扣件处板底点在2010年的纵向疲劳应力谱如图4和5所示，其他工况疲劳应力谱与此类似。

表6 温度梯度时程曲线最值

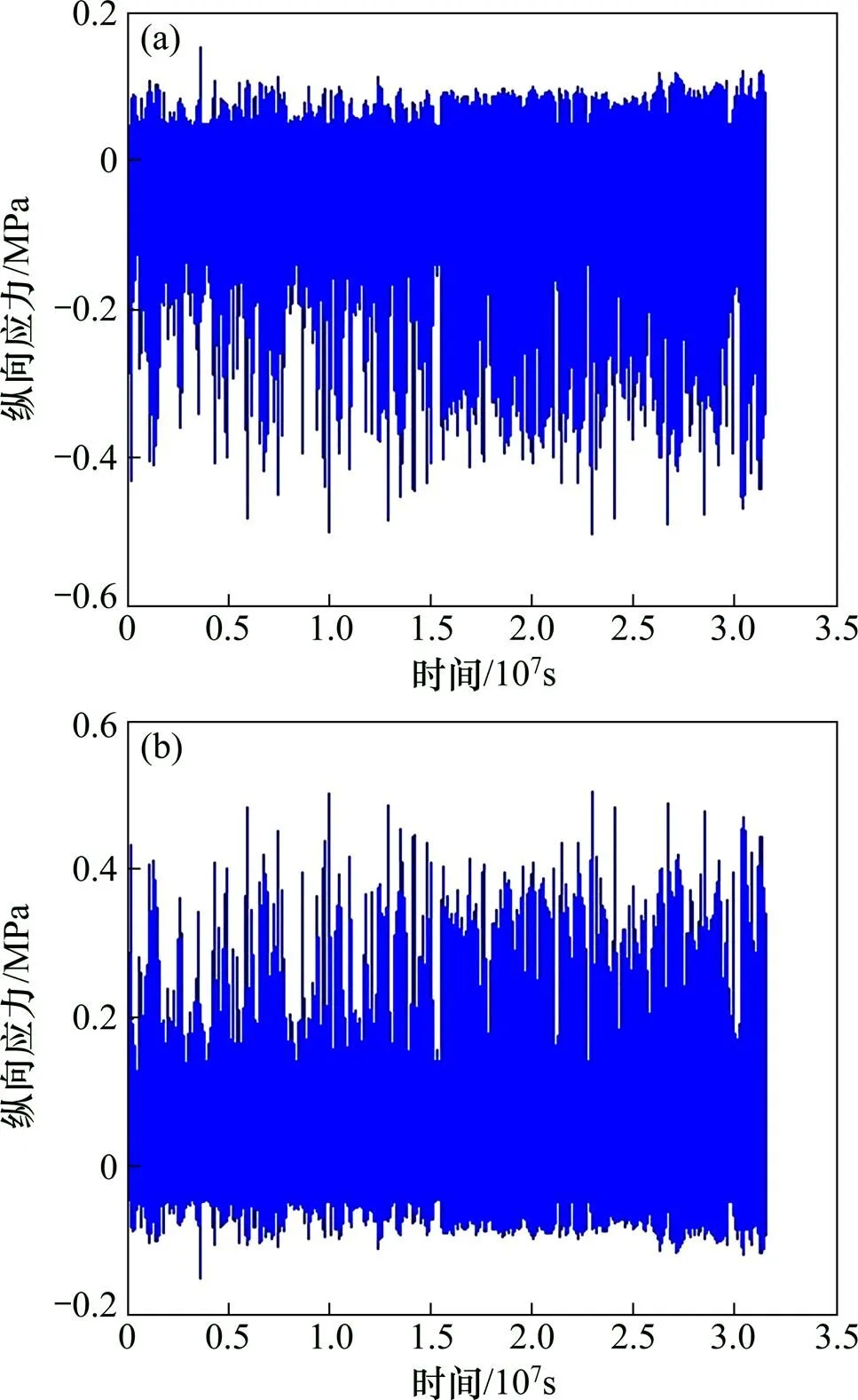
(a) 板顶点；(b) 板底点

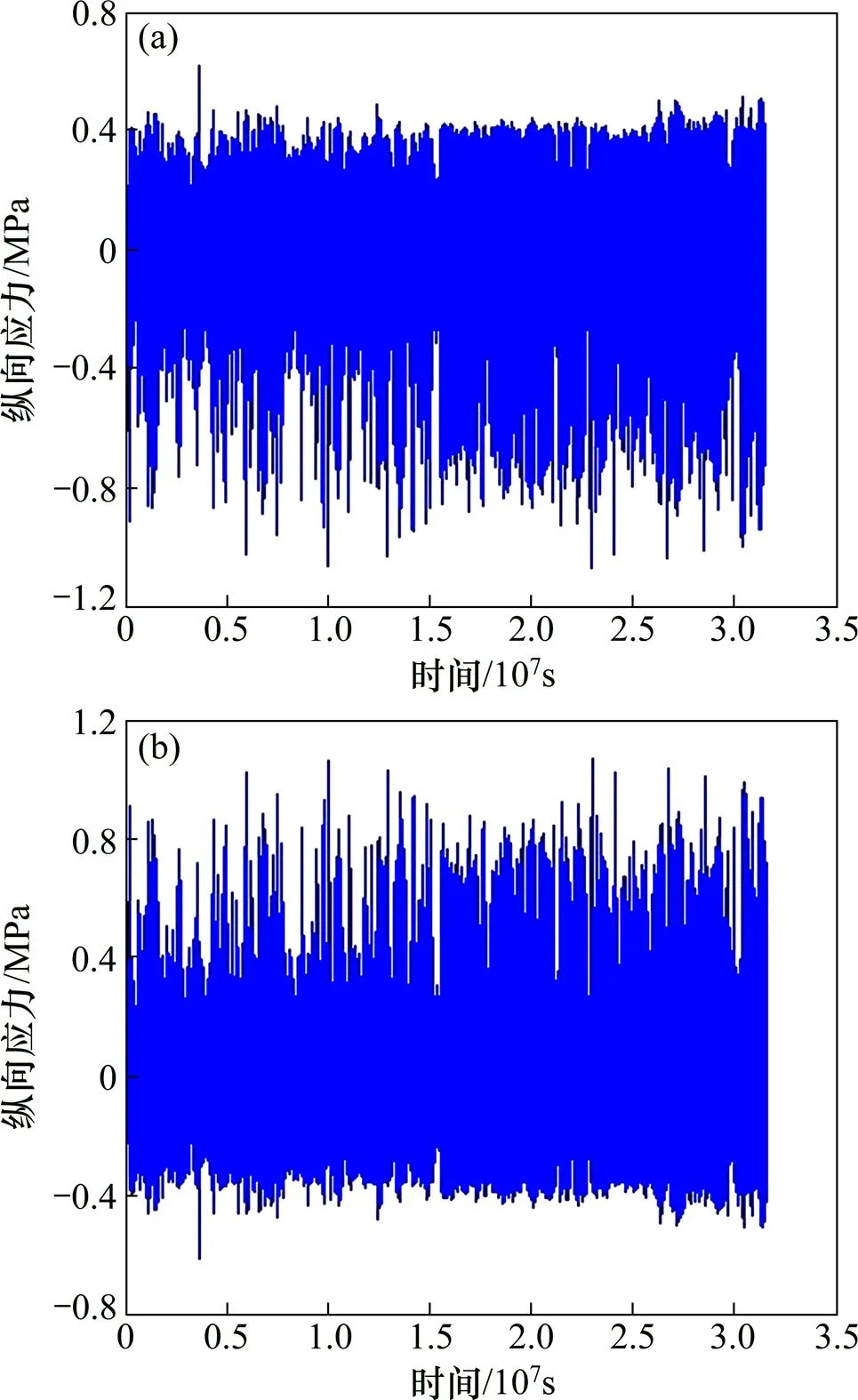
(a) 板顶点；(b) 板底点

为分析轨道板板厚和裂缝间距对服役期间温度梯度时程曲线和自重荷载作用下无砟轨道疲劳应力谱的影响，分别计算了服役期间温度梯度时程曲线和自重荷载作用下工况1~6疲劳应力谱。服役期间板端扣件处板顶点、板端扣件处板底点、板中扣件处板顶点和板中扣件处板底点纵向疲劳应力谱最值见表7。

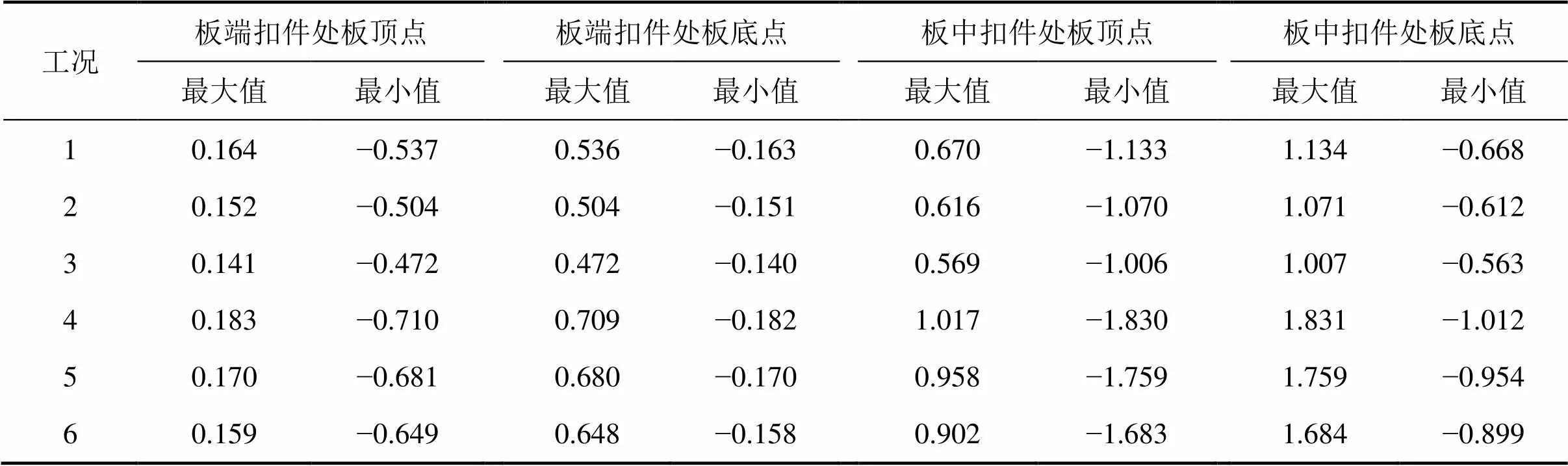
表7 不同工况纵向疲劳应力谱最值

3.3 计算结果分析

1) 板厚从190 mm增加至210 mm时，温度梯度时程曲线最大值减小2.4 ℃/m，温度梯度时程曲线最小值绝对值减小2.02 ℃/m。

2) 服役期间轨道板温度梯度时程曲线表现出明显的时变特性，即便是在气候条件接近的同一月份内也因每一天的气温、辐射和日照时间等不同而呈现较大变化。服役期间温度梯度时程曲线和自重荷载作用下纵连板式无砟轨道疲劳应力谱与温度梯度时程曲线变化紧密相关，具有明显的时变特性。

3) 服役期间板端扣件处板顶(底)点疲劳应力谱最值低于板中扣件处板顶(底)点疲劳应力谱最值，裂缝间距1.95 m时，板中扣件处板顶(底)点疲劳应力谱最值为板端扣件处板顶(底)点疲劳应力谱最值2.1~4.1倍；裂缝间距2.6 m时，板中扣件处板顶(底)点疲劳应力谱最值为板端扣件处板顶(底)点疲劳应力谱最值2.6~5.7倍。

4) 板厚从190 mm增加至210 mm时，服役期间无砟轨道疲劳应力谱最值逐渐减小，但降幅均在8%~16%之间。

5) 裂缝间距从1.95 m增加至2.6 m时，服役期间无砟轨道疲劳应力谱最值逐渐增大，板端扣件处板顶(底)点疲劳应力谱最值增幅最大达到37.5%，板中扣件处板顶(底)点疲劳应力谱最值增幅最大达到67.3%。

4 结论

1) 服役期间温度梯度时程曲线和自重荷载作用下纵连板式无砟轨道疲劳应力谱具有明显的时变 特性。

2) 板厚对温度梯度时程曲线和自重荷载作用下服役期间纵连板式无砟轨道疲劳应力谱影响较小，裂缝间距对其影响较大，为降低裂缝间距的影响，纵连板式无砟轨道裂缝间距不宜过大。

3) 服役期间纵连板式无砟轨道疲劳受列车荷载、不均匀沉降荷载、混凝土收缩荷载、温度梯度荷载等组合荷载的影响，本研究为服役期间组合荷载下纵连板式无砟轨道疲劳研究的一部分，可为服役期间组合荷载下纵连板式无砟轨道疲劳研究提供参考。

[1] 戴公连, 苏海霆, 闫斌. 圆曲线段无砟轨道横竖向温度梯度研究[J]. 铁道工程学报, 2014, 192(9): 40−45.
DAI Gonglian, SU Haiting, YAN Bin. Study on horizontal and vertical temperature gradient of ballastless track on curve line[J]. Journal of Railway Engineering Society, 2014, 192(6): 40−45.

[2] 赵坪锐. 客运专线无碴轨道设计理论与方法研究[D]. 成都: 西南交通大学土木工程学院, 2008: 72−125.
ZHAO Pingrui. Research on the design theory and method for ballastless track on passenger dedicated line[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2008: 72−125.

[3] 石现峰, 李建斌. 温度对板式无砟轨道结构的影响研究[J]. 铁道工程学报, 2008(5): 30−45.
SHI Xianfeng, LI Jianbin. Research on temperature effect on the structure of slab ballastless track[J]. Journal of Railway Engineering Society, 2008(5): 30−45.

[4] 杨义礼. 土质路基上CRTSI型板式轨道温度力研究[D]. 兰州: 兰州交通大学土木工程学院, 2012: 23−30.
YANG Yili. CRTSI plate rail temperature force on the soil subgrade[D]. Lanzhou: Lanzhou Jiaotong University. School of Civil Engineering, 2012: 23−30.

[5] 徐庆元．高速铁路无砟轨道国产化理论研究[R]．天津: 铁道第三勘察设计集团有限公司, 2008: 25−36.
XU Qingyuan. Calculation theory for designing home-made ballastless track of high speed railway[R]. Tianjin: The Third Railway Survey and Design Group Corporation, 2008: 25−36.

[6] 滕东宇. 桥上纵连板式无砟轨道底座板耐久性研究[D]. 北京: 北京交通大学土木工程学院, 2009: 34−48.
TENG Dongyu. Researeh on the durability of foundation plate in continuous-slab-track on bridge[D]. Beijing: Beijing Jiaotong University. School of Civil Engineering, 2009: 34−48.

[7] 王森荣, 孙立, 李秋义, 等. 无砟轨道轨道板温度测量与温度应力分析[J]. 铁道工程学报, 2009(2): 52−55.
WANG Senrong, SUN Li, LI Qiuyi, et al. Temperature measurement and temperature stress analysis of ballastless track slab[J]. Journal of Railway Engineering Society, 2009(2): 52−55.

[8] 中南大学土木工程学院. 双块式无砟轨道耐久性研究[R]. 长沙: 中南大学土木工程学院, 2009: 52−57.
School of Civil Engineering, Central South University. Study on durability of twin-block ballastless track[R]. Changsha: Central South University. School of Civil Engineering, 2009: 52−57.

[9] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006: 1−23.
YANG Shiming, TAO Wenquan. Heat transfer[M]. 4th ed. Beijing: Higher Education Press, 2006: 1−23.

[10] 戴公连, 郑鹏飞, 闫斌, 等. 日照作用下箱梁桥上无缝线路纵向力[J]. 浙江大学学报(工学版), 2013, 47(4): 609−614.
DAI Gonglian, ZHENG Pengfei, YAN Bin, etal. Longitudinal force of CWR on box girder under solar radiation[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(4): 609−614.

[11] Schindler A K, Ruiz J M, Rasmussen R O, et al. Concrete pavement temperature prediction and case studies with the FHWA HIPERPAV models[J]. Cement & Concrete Composites, 2004, 26(5): 463−471.

[12] 张建荣, 刘照球. 混凝土对流换热系数的风洞实验研究[J]. 土木工程学报, 2006, 39(9): 39−61.
ZHANG Jianrong, LIU Zhaoqiu. A study on the convective heat transfer coefficient of concrete in wind tunnel experiment[J]. China Civil Engineering Journal, 2006, 39(9): 39−61.

[13] CHEN Jiaqi, LI Liang, ZHAO Lianheng, et al. Solution of pavement temperature field in “Environment-Surface” system through Green’s function[J]. Journal of Central South University, 2014, 21(5): 2108−2116.

[14] Wang D, Roesler J R, Guo D Z. Analytical approach to predicting temperature fields in multilayered pavement systems[J]. Journal of Engineering Mechanics, 2009, 135(4): 334−344.

[15] 韩子东. 道路结构温度场研究[D]. 西安: 长安大学公路学院, 2001: 15−32.
HAN Zidong. Study on temperature field of road structure[D]. Xi’an: Chang’an University. School of Highway, 2001: 15−32.

Fatigue stress spectrum of longitudinally connected ballastless track under temperature gradient

XU Qingyuan, MENG Yajun, LI Bin, LOU Ping, YAN Bin

(School of Civil Engineering, Central South University, Changsha 410075, China)

In order to research the fatigue stress spectrum of longitudinally connected ballastless track under temperature gradient in the period of service, calculation models of temperature gradient based on heat transfer theory and fatigue stress spectrum of slab under temperature gradient were established and verified respectively. Taking meteorological data of Guangzhou for example, temperature gradient time-history curve of slab in the period of service was calculated with verified model firstly, and then fatigue stress spectra in the period of service of longitudinally connected ballastless track with different thicknesses and fracture intervals were calculated with verified model under self weight and temperature gradient time-history curve. The results show that the fatigue stress spectrum in the period of service of longitudinally connected ballastless track under temperature gradient has obvious time-varying characteristics. The thickness of slab has little influence on the fatigue stress spectrum in the period of service of longitudinally connected ballastless track under temperature gradient time-history while fracture interval has great influence on it.

railway engineering; heat transfer theory; temperature gradient; longitudinally connected ballastless track; fatigue stress spectrum

U213

A

1672−7207(2015)02−0736−06

2014−01−13；

2014−04−20

国家自然科学基金资助项目(51178469）；国家留学基金资助项目(201208430112)；国家自然科学基金−教育部高铁基础研究联合基金资助项目(U1334203)；中央高校基本科研业务费专项资金资助项目(2012zzts088)(Project (51178469) supported by the National Natural Science Foundation of China; Project (201208430112) supported by the State Scholarship Fund of China Scholarship Council; Project (U1334203) supported by National Natural Science Joint High Speed Railway Foundation of China; Project (2012zzts088) supported by the Fundamental Research Funds for the Central Universities)

徐庆元，博士，副教授，从事高速铁路无缝线路及无砟轨道研究；E-mail：xuqingyuan1972@163.com

10.11817/j.issn.1672-7207.2015.02.049

(编辑 赵俊)