基于粒子群优化的自然电场数据反演

朱肖雄，崔益安，李溪阳，佟铁钢，纪铜鑫



基于粒子群优化的自然电场数据反演

朱肖雄1, 2，崔益安1, 2，李溪阳1, 2，佟铁钢1, 2，纪铜鑫1, 2

(1. 中南大学 地球科学与信息物理学院，湖南 长沙, 410083；2. 中南大学 有色资源与地质灾害探查湖南省重点实验室，湖南 长沙，410083)

在分析测试粒子数、速度因子、目标函数等算法参数对粒子群优化算法效果的影响规律的基础上，设计自然电场粒子群优化反演算法，并对加入不同程度白噪声模拟数据进行反演试算。研究结果表明：设计的粒子群优化算法能有效实现对自然电场数据的反演，算法具有收敛速度快、稳定、反演精度较高和抗噪音能力强等优点，可以较为准确地得到异常体的位置、形态、极化角等参数，能较好地满足生成实际要求。

自然电场；反演；粒子群优化；参数分析

自然电场法是一种基于岩、矿石天然产生电位差的观测方法。自然电场法除了应用在传统的金属硫化物和石墨[1]等矿产勘查领域外，近年来在环境和工程地球物理领域的应用越来越广泛，主要应用于堤坝的渗漏检测[2−3]、地下水调查[4]和孔洞检测[5]等。在这些应用中，经常需要圈定如矿脉、渗漏点、孔洞这类异常体。这些异常体通常可以近似成单个球体、圆柱体和板状体等简单几何模型或多个简单几何模型的组合。一些图形和数值的方法已经被用来解释自然电位异常，如特征点法[6]、曲线拟合法[7]、最小二乘法[8]、梯度法[9]、傅里叶分析法[10]、校正平均残余异常法 等[11]。特征点法和曲线拟合法比较繁琐并且反演效果不佳。后几种方法当测量数据有干扰时，反演结果会受到较大的影响，因此，很有必要采用抗干扰能力强的方法来反演自然电场数据。粒子群优化算法(PSO)是Kennedy等于1995年提出的一种新颖的进化算 法[12]，它是一种基于群智能的算法，通过模拟鸟集群飞行觅食的行为来达到最优化的目的。该算法已经成功地应用于很多领域，例如信号处理[13]、图像处理[14]以及岩土力学等[15]。近年来，粒子群优化算法在地球物理领域的应用研究[16−18]也越来越多。例如，崔益安等[19−20]将粒子群优化算法用于激电数据的联合反演和中梯电阻率多异常体反演的研究。Fernando等[21−22]开展了关于自然电位异常数据反演的研究，并证明了粒子群优化算法是一种有效的反演自然电位异常数据的方法，但其只对10%噪音模拟数据进行了测试。考虑到自然电场数据易受干扰而导致实际噪音干扰远大于10%，为了实现抗噪音能力更强的反演算法，本文作者研究了粒子群优化算法参数对算法效果的影响规律，以期通过更佳的参数设置来提高算法的性能和抗噪音能力。

1 正演计算

地下极化球体模型如图1所示。假设在均匀充满电阻率为1的介质里，有1个电阻率为2、半径为0的球体。当球体被均匀极化时，球体表面形成不均匀的(异常)双电层，其电位差Δ(近似看作是偶电层的电位跃变值)随极化方向的坐标呈线性变化。均匀极化球体内、外电位的分布以极化轴为对称轴，与方位角无关，故满足球坐标系的拉普拉斯方程：

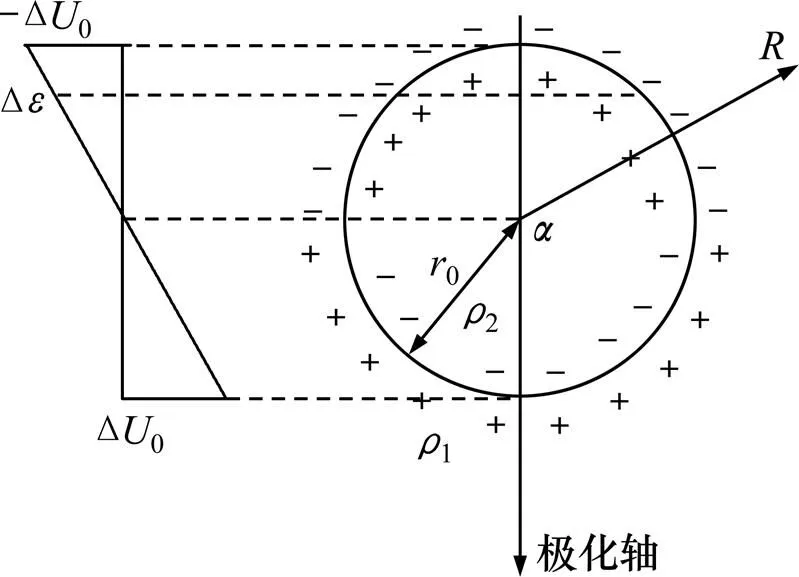
图1 地下极化球体模型

有边界条件为

式中：1和2分别为球体的外部和内部电位；1n和2n为球体内外法向的电流密度。

地下异常源模型如图2所示。通过分离变量法解得空间内任意一点的自然电位异常为：

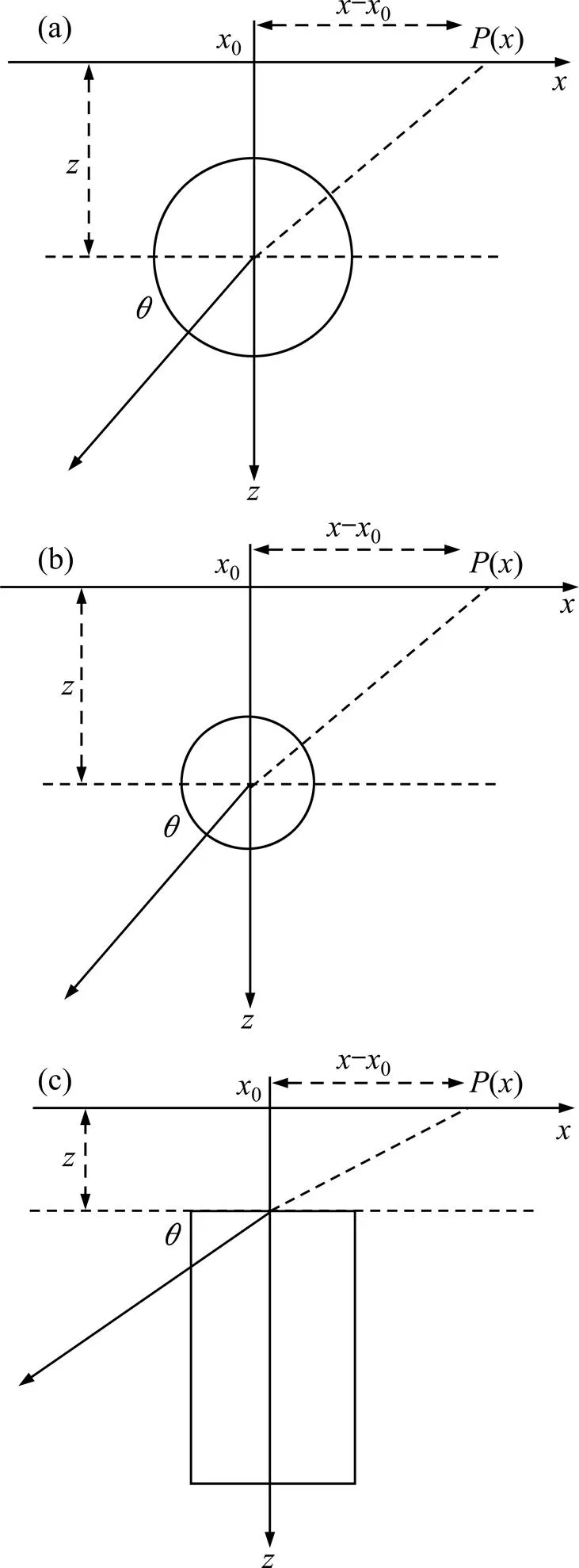
(a) 球体模型；(b) 水平圆柱体模型；(c) 垂直圆柱体模型

当极化轴偏转与负半轴呈时，如图2(a)所示，可推出地表的自然电位异常公式为：

类似地，可推出地下水平圆柱体和垂直圆柱体的自然电位异常公式分别为：

综合式(5)~(8)可得类球体的地表自然电位异常公式：

其中：为埋藏源的深度；为极化角度；为形状因子，0为异常源的坐标，为电偶极矩。形状因子取值为1.5，1.0，0.5时分别表示球体、水平圆柱体和垂直圆柱体。在异常源地表处(=0)的异常值为

地下异板状模型如图3所示。设在均匀充满电阻率为的介质里，有一倾斜板状体。空间中电位分布为：

其中：1和2分别为倾斜板状体两端到空间某一点的距离；为单位长度上的电流；′为电偶极矩。

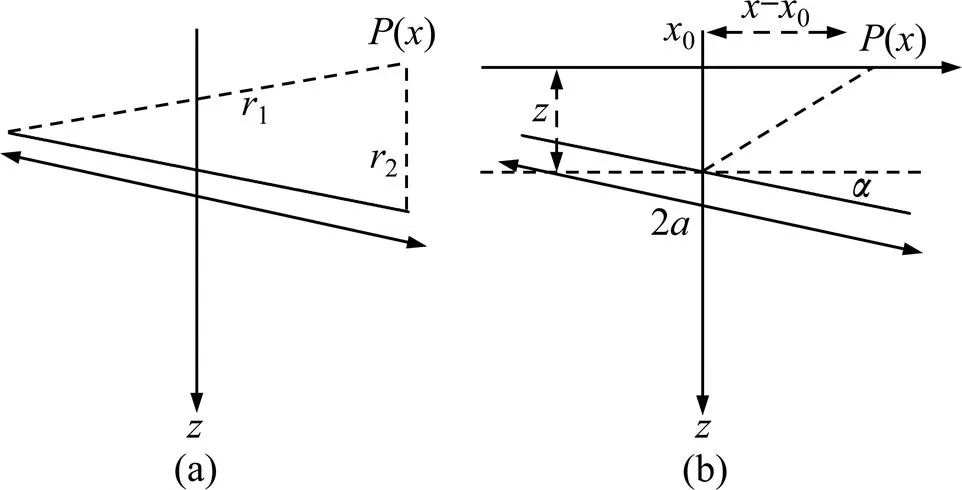
(a) 模型示意图；(b) 模型坐标图

可推出地表上的自然电位异常式为

其中：为倾斜板状体的倾斜角度；为倾斜板状体长度的1/2；0为异常源的坐标；为倾斜板状体中心的深度。

2 粒子群优化算法的设计

粒子群优化算法的基本思想是随机初始化一群粒子，将每个粒子视为优化问题的1个可行解，粒子的好坏由一个事先设定的目标函数来确定。每个粒子将在可行解空间中运动，并由1个速度变量确定其方向和距离。通常粒子将追寻当前的最优粒子，经过多次迭代得到最优解。

自然电位异常的粒子群优化反演算法具体的设计流程如下。

1) 设定搜索空间，即反演参数的上、下界。设置迭代过程中的最大迭代次数max，粒子更新速度范围为[min，max]，

式中：为比例系数；||为搜索范围的上界。

2) 初始化粒子群位置和更新速度。标记初始粒子群位置为粒子群最优位置Best，通过目标函数算评价得到粒子群中的最优粒子。

3) 粒子的状态更新，通过式(15)和式(16)更新每一个粒子的速度和位置。

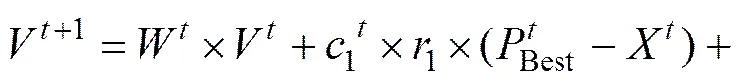
式中：W为惯性权重；start取0.9，end取0.4；，为速度因子，根据速度因子策略更新；Best为当前粒子群的最优位置；为迭代次数；1和2为在(0,1)之间的随机数。

4) 对粒子进行评价，通过目标函数评价粒子群X+1，更新粒子群最优位置和最优粒子。

5) 迭代至预设的最大迭代次数max。输出反演 结果。

根据反演结果，通过单一变量法对粒子数、速度比例系数、速度因子策略、和目标函数进行分析比对，如图4所示。

(a) 粒子数分析；(b) 速度比例因子分析；(c) 学习因子策略分析；(d) 目标函数分析

通过测试，在迭代次数max取200，粒子数取50，速度比例系数取0.1，线性递减速度因子策略，目标函数选择式(18)时，基于粒子群优化的自然电场反演的效果较好。

3 反演示例

首先对单个异常体模型的正演计算数据进行反演测试。为了便于比较分析反演效果，采用了与文献[22]相同的地电模型参数，具体参数为：垂直圆柱体(=4 m，=0.5，=40°，=−500 mV，0=−321.39 mV，0=0 m)和倾斜板状体模型(=10 m，=5 m，=35°，0=8 m，′=150 mV)。为了测试抗噪音能力，对模拟数据加入10%~30%的随机噪音再进行反演。其中反演结果误差的评价表达式为

分别在理想情况下和加入噪音的状态下对单个异常体的模拟数据进行反演，结果如图5和图6所示。由图5(a)和图6(a)可见：粒子群优化反演曲线与正演模拟的曲线完全相同。说明了粒子群优化反演和有很高的反演精度。在加入了10%~30%的噪音情况下，具体数值如表1和表2所示。粒子群优化反演仍然获得了很好的反演效果，说明该算法有较强的抗噪音能力。

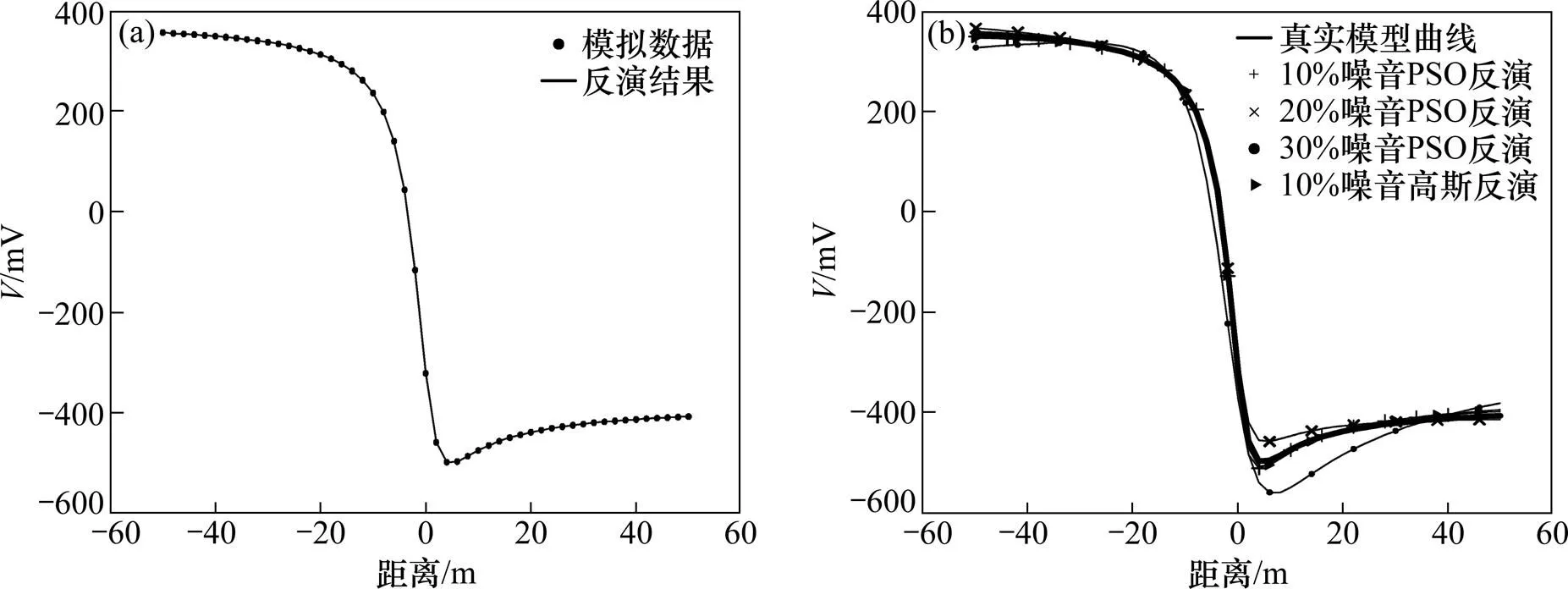
(a) 理想模拟数据反演结果；(b) 带噪音的模拟数据反演结果

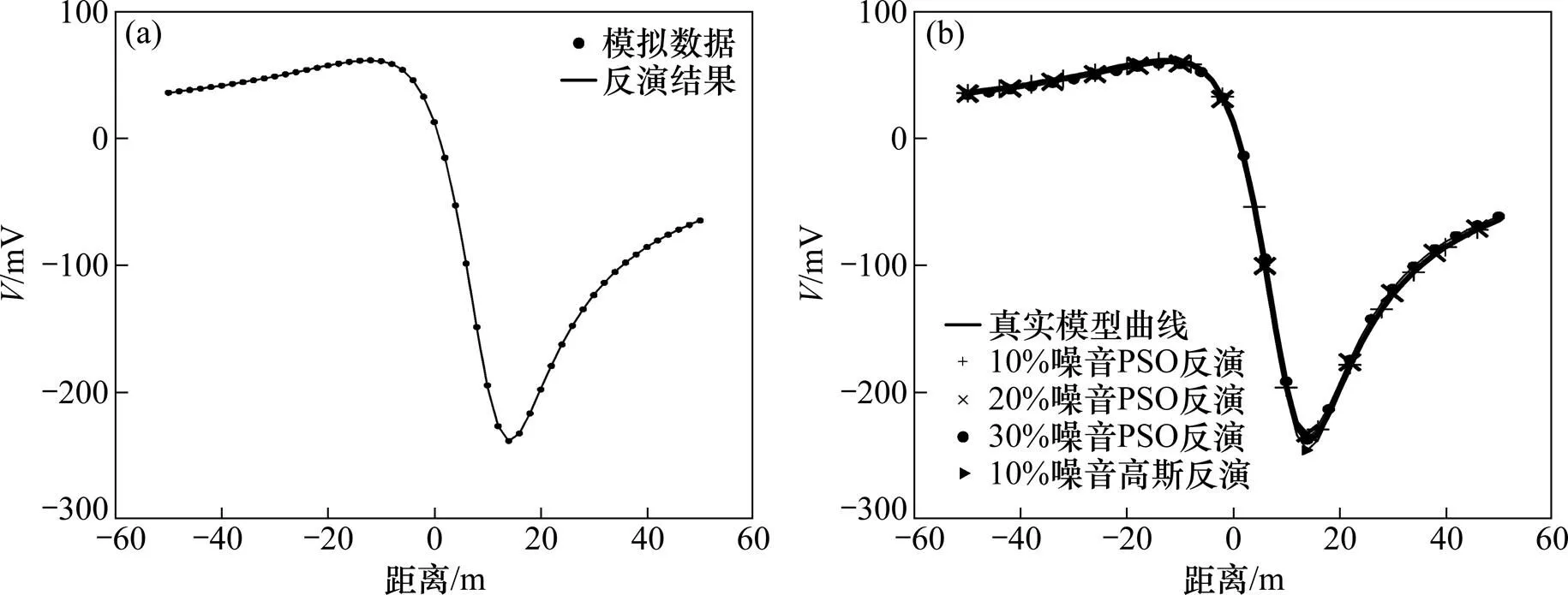
(a) 理想模拟数据反演结果；(b) 带噪音的模拟数据反演结果

表1 垂直圆柱体理想数据及噪音数据的PSO反演结果

表2 倾斜板状体理想数据及噪音数据的PSO反演结果

同时，用传统的高斯算法对模拟数据进行反演，反演结果如表3和表4所示。由反演结果可知：无噪音和噪音较小时，高斯反演的参数精度很高；随着噪音加大，高斯法反演的参数精度要比粒子群反演的精度低，且高斯反演严重依赖初始值设置，在目标函数具有多极值的情况下，很难设置合适的初值，而若设置稍有不当，则会发散，反演不出结果。

表3 垂直圆柱体理想数据及噪音数据的高斯反演结果

表4 倾斜板状体理想数据及噪音数据的高斯反演结果

对多个异常模型的正演模拟数据进行反演测试。测试的模型由1个球体模型(=2.6 m，=1.5，=40°，=−1 615 mV，0=−75 mV，0=−55 m)和1个倾斜板状体模型(=5 m，=3 m，=30°，0=6 m，′=102 mV)组成。并对加入了10%~30%的随机噪音的模拟数据进行测试。在理想情况下和带噪应条件下对多个异常体的模拟数据反演结果，对比如图8所示。由图8可见：反演曲线与正演曲线完全相同。说明反演算法具有同时反演多个目标体的能力，且反演精度很高。在加入10%~30%噪音的情况下对多个异常体的模拟数据进行反演，粒子群优化反演具有很强的抗噪音能力。反演效果完全能满足对异常体的位置、形态、极化角、埋深参数准确估计的要求。

(a) 理想模拟数据反演结果；(b) 带噪音的模拟数据反演结果

4 结论

1) 粒子群优化反演对单个和多个异常体的反演效果都很好，反演精度高，收敛速度快，抗噪音干扰能力强。且由于正演计算很快，在迭代200次的情况下，耗时可忽略不计，反应效率很高。相比于传统的线性算法，粒子群优化算法的优点在于不用设置初值，前期搜索全局，后期搜索局部，不易发散。这种快速的高精度反演具有重要实际意义。

2) 下一步的研究重点并通过对典型实测数据进行反演，检验算法实用性。

[1] 李林, 解立发. 自然电场法在晶质石墨资源勘查中的应用[J]. 中国非金属矿工业导刊, 2006, 52: 57−60.
LI Lin, XIE Lifa. Self-potential method in the application of graphite exploration[J]. China Non-metallic Mining Industry Herald, 2006, 52: 57−60.

[2] 王绍彪, 汤浩. 综合物探方法在探测基坑围堰渗漏中的应用[J]. 人民珠江, 2011, 32(Z1): 52−53.
WANG Shaobiao, TANG Hao. Comprehensive Geophysical method in the application of detecting leaks on foundation pits and cofferdam[J]. Pearl River, 2011, 32(Z1): 52−53.

[3] 孙士安. 伏漫水库主坝渗漏通道勘察方法[J]. 广西水利水电, 2012(1): 12−15.
SUN Shian, Reconnaissance method of detecting leaks in passages on main dam of Fuman reservoir[J]. Guangxi Water Resources & Hydropower Engineering, 2012(1): 12−15.

[4] 刘加文, 王治军, 杜志伟. 自然电场法在场地地下水勘查中的应用[J]. 工程地球物理学报, 2009, 6(5): 612−615.
LIU Jiawen, WANG Zhijun, DU Zhiwei. Application of natural electric field in site groundwater exploration[J]. Chinese Journal of Engineering Geophysics, 2009, 6(5): 612−615.

[5] Jardani A, Revil A, Santos F A M, et al. Detection of preferential infiltration pathways in sinkholes using joint inversion of self-potential and EM-34 conductivity data[J]. Geophysical Prospecting, 2007, 55(5): 749−760.

[6] Sharma S P, Biswas A. Interpretation of self-potential anomaly over a 2D inclined structure using very fast simulated-annealing global optimization - An insight about ambiguity[J]. Geophysics, 2013, 78(3): WB3−WB15.

[7] El-Araby H M. A new method for complete quantitative interpretation of self-potential anomalies[J]. Journal of Applied Geophysics, 2004, 55(3/4): 211−224

[8] Abdelrahman E M, Essa K S, Abo-Ezz E R, et al. New least-square algorithm for model parameters estimation using self- potential anomalies[J]. Computers & Geosciences, 2008, 34: 1569−1576.

[9] Abdelrahman E M, El-Araby H M, El-Araby T M, et al. New methods for shape and depth determinations from SP data[J]. Geophysics, 2003, 68(4): 1202−1210.

[10] Fedi M, Abbas M A. A fast interpretation of self-potential data using the depth from extreme points method[J]. Geophysics, 2013, 78(2): E107−E116.

[11] Abdelrahman E M, El-Araby T M, Essa K S. Shape and depth determinations from second moving average residual self-potential anomalies[J]. Journal of Geophysics and Engineering, 2009(6): 43−52.

[12] JIE Jing, ZENG Jianchao, HAN Chongzhao, et al. Knowledge- based cooperative particle swarm optimization[J]. Applied Mathematics and Computation, 2008, 205(2): 861–873

[13] Jun S, Wei F, Wenbo X. A quantum-behaved particle swarm optimization with diversity- guided mutation for the design of two-dimensional IIR digital filters[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2010, 57(2): 141−145.

[14] Hao G. Multilevel thresholding for image segmentation through an improved quantum- behaved particle swarm algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(4): 934−946.

[15] 杨文东, 张强勇, 李术才, 等. 粒子群算法在时效变形参数反演中的应用[J]. 中南大学学报(自然科学版), 2013, 44(1): 282−288.
YANG Wendong, ZHANG Qiangyong, LI Shucai, et al. Application of particle swarm optimization in time-dependent parameters[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 282−288.

[16] SONG Xianhai, TANG Li, LÜ Xiaochun, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2012, 84: 1−13.

[17] 师学明, 肖敏, 范建柯, 等. 大地电磁阻尼粒子群优化反演法研究[J]. 地球物理学报, 2009, 52(4): 1114−1120.
SHI Xueming, XIAO Min, FAN Jianke, et al. The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J]. Chinese Journal of Geophysics, 2009, 52(4): 1114−1120.

[18] 蔡涵鹏, 贺振华, 高刚, 等. 基于混合优化算法的地震数据匹配追踪分解[J]. 中南大学学报(自然科学版), 2013, 44(2): 687−694.
CAI Hanpeng, HE Zhenghua, GAO Gang. Seismic data matching pursuit using hybrid optimization algorithm and its application[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 687−694.

[19] 崔益安, 李溪阳, 向恩明, 等. 基于粒子群优化的双频激电数据联合反演[J]. 中国有色金属学报, 2013, 23(9): 2498−2505.
CUI Yian, LI Xiyang, XIANG Enming, et al. Joint inversion of dual frequency IP data using PSO[J], The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2498−2505.

[20] 崔益安, 纪铜鑫, 李溪阳, 等. 基于粒子群优化的多目标体中梯电阻率异常反演[J]. 地球物理学进展, 2013, 28(4): 2164−2170.
CUI Yian, Ji Tongxin, Li Xiyang, et al. Inversion of multi-anomalies in resistivity profiling based on particle swarm optimization[J]. Progress in Geophysics, 2013, 28(4): 2164−2170.

[21] Fernando A, Monteiro Santos. Inversion of self-potential of idealized bodies’ anomalies using particle swarm optimization[J]. Computers & Geosciences, 2010, 36: 1185−1190.

[22] Peksen E, Türker Y,A Yekta K, et al. Application of particle swarm optimization on self-potential data[J]. Journal of Applied Geophysics, 2011, 75(2): 305−318.

Inversion of self-potential anomalies based on particle swarm optimization

ZHU Xiaoxiong1, 2, CUI Yian1, 2, LI Xiyang1, 2, TONG Tiegang1, 2, JI Tongxin1, 2

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;2. Hunan Key Laboratory of Non-ferrous Resources and Geological Hazard Detection,Central South University, Changsha 410083, China)

Based on testing and analyzing relevant parameters including particle quantity, rate scale factor, objective function etc., the particle swarm optimization (PSO) was used to design inversion algorithm for self-potential data. Through adding different degrees of Gauss noise, the synthetic data was used to test the designed inversion algorithm. The results show that the PSO algorithm can effectively realize the inversion of self-potential data with fast and stable convergence, high inversion accuracy and high anti-noise capability. Through the designed algorithm, the parameters contain origin of the anomaly, shape, polarization angle, etc, can relativey accurately be obtained and can meet the demands of engineering investigation and mineral exploration.

self-potential; inversion; particle swarm optimization; parameter analysis

P631

A

1672−7207(2015)02−0579−07

2014−03−06；

2014−06−20

国家自然科学基金资助项目(41274122，41374119)；教育部博士点基金资助项目(20110162130008)；国家科技支撑计划项目(2011BAB04B08)；国家科技基础性工作专项(2013FY110800)(Projects (41274122, 41374119) supported by the National Natural Science Foundation of China; Project (20110162130008) supported by the Doctoral Fund of Ministry of Education of China; Project (2011BAB04B08) supported by the Special Basic Scientific Project of China; Project (2013FY110800) supported by the National Special Basic Scientific Program of China)

崔益安，博士，副教授，从事物探方法与数据处理研究；E-mail：cuiyian@csu.edu.cn

10.11817/j.issn.1672-7207.2015.02.028

(编辑 赵俊)