基于矩形双窗的滑动DTFT高精度相位差测量算法

沈廷鳌，涂亚庆，张海涛，李明



基于矩形双窗的滑动DTFT高精度相位差测量算法

沈廷鳌，涂亚庆，张海涛，李明

(后勤工程学院 信息工程系，重庆，401311)

针对机械振动中频率很低或接近奈奎斯特频率的信号，采用传统的相位差测量方法存在较大误差，为更好地抑制频谱泄露的影响，提高相位差测量精度，在传统DTFT算法的基础上，采用矩形双窗、计及负频率影响以及滑动递推，提出一种基于矩形双窗的滑动DTFT高精度相位差测量算法，并阐述该算法原理及其实现步骤。研究结果表明：该算法计算量较小，实现简单，应用于相位差测量，有效地减小了频谱泄露引起的测量误差，能够获得比传统加窗DTFT算法更高的相位差计算精度。仿真和实验结果验证了本文算法的可行性和有效性。

相位差；DTFT；余弦窗；频谱泄露；负频率

振动信号的相位差测量在信号分析、工业测量、故障诊断、电力系统及通信等领域都有着广泛应用。例如，在高精度流量测量领域得到广泛应用的科氏流量计，就是通过测量两路同频振动信号之间的相位差来测量流体质量流量的[1]。由于2路振动信号的相位差一般小于4°，且相位差的精度直接影响流体质量测量精度，因此，实现对相位差的高精度测量显得尤其重要。目前，测量相位差的方法较多，其中数字相关法[2−3]和频谱分析法[4−7]是应用和研究较多的2种方法。数字相关法具有较强的噪声抑制能力，但难以消除谐波干扰，且要求对周期信号实行严格整周期采样。频谱分析法是利用傅里叶变换将时域信号变换到频域信号再进行处理，算法要求同步采样。在非同步采样的条件下，为提高测量精度，通常采用加窗的办法来减小频谱泄露的影响。然而，当信号频率很低或者接近奈奎斯特频率(即采样频率的一半)时，上述方法的测量精度均不太高，且此类信号在仪器仪表、振动工程、状态检测与故障诊断等领域均大量存在。例如：当待测信号频率较低、采样频率远高于待测频率时，待测频率在频谱中处于相对低频的位置[8−9]。在故障诊断领域，受硬件条件及成本等因素的影响，当现有采样装置的采样频率限定为1 024 Hz时，旋转机械转子系统松动故障产生的10倍频间谐分量为500 Hz(信号基频为50 Hz，10倍频间谐分量为10×50 Hz=500 Hz)，信号频率就接近奈奎斯特频率[10−11]。对此类信号进行分析，除了频谱泄露和栅栏效应外，负频率成分的干涉也是影响其精度的重要原因。如何减小频谱泄露和负频率成分的影响，已引起很多学者们的关注，但测量精度有待进一步提高，计算复杂度有待进一步降低。为此，本文作者在传统DTFT算法的基础上，采用矩形双窗、计及负频率影响以及滑动递推的思想，提出一种基于矩形双窗的滑动DTFT相位差测量算法，阐述算法原理及实现步骤，并与传统加窗DTFT(discrete time Fourier transform)算法的测量误差进行了仿真比较分析。

1 算法原理及实现步骤

1.1 矩形双窗

数字化测量相位差，观测信号的时间总是有限的，需要对原有长序列进行1次截断。截断就会造成频谱泄露，进而产生测量误差。加窗函数就是对被分析信号在不同时刻加不同权值，以尽可能地减小截断所造成的影响。

长度为的矩形窗时、频域表达式分别为

通过将2个长度为的矩形窗进行卷积运算，得到1个长度为2−1的新序列，在新序列的首部或尾部加上1个0，即可得到长度为2的矩形双窗[12]。本文在首部加0，并令=2，可得矩形双窗的时域和频域表达式分别为：

为便于比较，给出相同长度=32的矩形双窗与矩形窗的频域图，如图1所示。从图1可以看出：矩形双窗具有更快的旁瓣衰减速率，采用该窗对信号进行加权处理，可有效抑制频谱泄露的影响。图2和图3所示分别为单一频率正弦信号加矩形窗和加矩形双窗后得到的幅度频谱。从图2与图3可以看出：当信号频率较低或接近Nyquist频率时，旁瓣干涉较大，在进行频谱分析时，必须计及负频率成分的影响；在相同条件下，采用加矩形双窗所取得的效果比加矩形窗的效果好。

1—矩形窗；2—矩形双窗

ω：(a) 0.4π；(b) 0.1π；(c) 0.9π

ω：(a) 0.4π；(b) 0.1π；(c) 0.9π

此外，参照矩形双窗的构造过程，采用窗Hanning，Blackman和Blackman-Harris，也可构造得到组合双窗DHanning，DBlackman和 DBlackman- Harris。通过仿真研究发现，主瓣的宽度随着余弦窗阶数的增加而增大，频谱的分辨率随着余弦窗的阶数的增加而降低，所以，一般选取余弦窗的阶数不宜过大。本文经综合考虑，选择矩形双窗进行研究。

1.2 加窗的DTFT算法

传统的DTFT法忽略了频谱中的负频率成分，影响了相位差的计算精度。本文计及负频率的影响，提出一种加矩形双窗的滑动DTFT相位差测量算法，以用于振动信号相位差的高精度测量。算法原理如下。

设2路同频率的实正弦信号为

式中：=0，1，…，−1；1和2为信号的幅度；1和2为信号的初相。设为的估计值，用长度为的矩形双窗对信号进行加权截断，得到加矩形双窗信号在处的DTFT为

需要说明的是：根据频域卷积定理，时域相乘对应于频域卷积，因此，也可理解为

进而求得

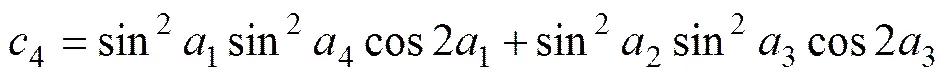
在一般情况下，当信噪比不是特别低时，采用陷波器或离散频谱校正的方法所求得信号的频率值与真实值很接近，可近似认为，，代入式(9)可得

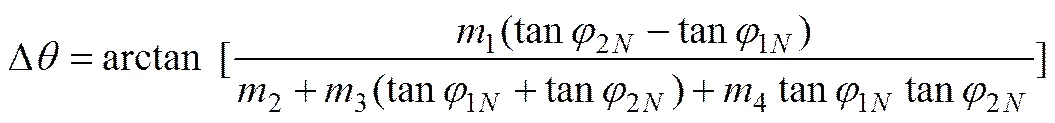
式中：

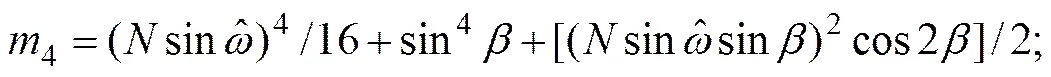
1.3 滑动DTFT递推算法

对于观测信号()，设时刻开始采样得到个采样数据()，(+1)，…，(+−1)，这个数据可理解为采用宽度为的矩形窗对信号进行截取所得到的，则该有限长序列的DTFT为

在+1时刻，得到新采样点(+)，剔除(),则由个采样数据(+1)，(+2)，…，(+−1)，(+)组成的新的采样序列在处的DTFT为

式(13)即为滑动DTFT递推公式[13]。可见：相邻2个矩形窗存在递推关系，每采入1点新的数据后，只需进行2次复数加法和2次复数乘法，消除了冗余计算，且不存在叠加溢出的问题，大大降低了计算量，并能反映实际信号频率变化的特性。

1.4 算法实现步骤

归纳起来，本文所提的基于矩形双窗的滑动DTFT相位差测量算法的实现步骤如下：

2) 在第1个矩形窗内的采样序列进行常规DTFT运算。

5) 利用滑动DTFT递推式(13)，求出2路信号在任意指定频率处的DTFT。

6) 重复步骤3)和4)，从而可求得2路信号在任意时刻的相位差。

需要指出的是：基于矩形双窗的滑动DTFT相位差计算公式的推导过程中，由于未进行任何近似和省略，因此，在无噪声背景下，当已知时，通过式(10)求得的相位差在理论上误差为0°；当未知时，的估计值越准确，则相位差的计算精度越高。同时，在获知的情况下，通过式(8)还能准确求解出信号的初相。此外，本文算法采用滑动递推的思想，避免了冗余计算，减小了计算量，提高了算法的实时性。

2 实验分析

为验证本文所提出的方法的有效性，采用单一频率实正弦信号，对本文方法(加矩形双窗)和DTFT法，分别在无噪声、有噪声和采样点数变化的情况下进行仿真验证。仿真中，采样点数取1 024点，采样频率为1 kHz，频率分辨率为0.976 6 Hz，2路信号的相位差为1.8°。

2.1 噪声的影响

图4所示为无噪声背景下频率很低或接近Nyquist频率时，2种方法在不同频率处相位差测量的相对误差。信号频率取值范围分别为0.5~2.5 Hz和497.5~499.5 Hz，变化步长均为0.05 Hz。从图4可以看出：当频率很低或接近Nyquist频率时，传统DTFT方法的测量误差均较大，而本文方法均具有很高的测量精度。其原因为：在频率很低或接近Nyquist频率时，旁瓣干涉较大，本文方法采用加矩形双窗并计及了负频率成分的影响，有效地抑制了频谱泄露的影响，所以能获得较高的测量精度。

(a) 频率很低；(b) 接近Nyquist频率

当信噪比为30 dB，针对频率很低或接近Nyquist频率时，分别采用DTFT法和本文方法经200次独立仿真实验得到的相位差估计均方误差随频率变化曲线如图5所示。从图5可以看出：频率在0.5~2.5 Hz的变化过程中，DTFT法的测量精度随着频率的增大有逐渐增大的趋势，其中在1.0，1.5，2.0和2.5 Hz附近精度较高，接近本文方法计算精度，而本文方法始终保持着较高的测量精度；频率在497.5~499.5 Hz的变化过程中，DTFT法的测量精度随着频率的增大有逐渐减小的趋势，其中在497.5，498.0，498.5和499.0 Hz附近精度较高，接近本文方法计算精度，而本文方法也始终保持着较高的测量精度。其原因为：在频率很低(靠近0.5 Hz这端)或接近Nyquist频率(靠近499.5 Hz这端)时，负频率成分会产生旁瓣干涉，进而影响相位差的测量精度；在频率远离这两端时，负频率成分影响较小；当信号频率等于频率分辨率的一半的整数倍时，信号频率处的DTFT的负频率部分为0，此时不存在负频率影响，这2种方法均可获得较高的测量精度。本文方法考虑了负频率成分的影响，并采用加矩形双窗，有效地抑制了频谱泄露的影响，所以，能始终保持着较高的测量精度。

(a) 频率很低；(b) 接近Nyquist频率

2.2 采样点数变化的影响

在迭加白噪声的情况下，取信号频率为2.5 Hz，采样点数在200~1 000范围内变化时相位差均方误差的变化曲线如图6所示。从图6可以看出：当信号频率等于频率分辨率的一半的整数倍时，负频率成分为0，DTFT法精度接近本文方法精度；随着采样点数的增加，DTFT法的测量精度明显提高，而本文方法的测量精度提高较小；本文方法始终能保持着较高的测量精度，说明本文方法在较少采样点数的情况下也可获得较高的测量精度。此外，仿真还表明：当采样点数增加到满足一定采样点数的情况下，相位差的测量误差变化很小。

1—DTFT法；2—本文方法(加矩形双窗)

2.3 在科氏流量计中的应用

为考察本文所提方法的相位差测量精度，仿真模拟科氏流量计相位差测量实验以进行比较分析。首先产生2路加高斯白噪声的正弦信号，采用自适应格型陷波器进行滤波以求其频率，然后对滤波后的信号分别采用DTFT法和本文方法测量相位差。流量计振动信号的频率为146 Hz(采样频率远高于信号频率，可视为频率很低的情况)，采样频率为10 kHz，采样点数为20 000，信噪比为20 dB，相位差呈线性变化。由于陷波器存在一个收敛过程，为去除收敛过程带来的影响，选取从4 000点以后开始进行相位差计算，图7所示为这2种方法的相位差估计曲线。由图7可以看出：本文方法在噪声条件下，能实时跟踪相位差的线性变化，能始终保持着较高的测量精度；而DTFT法随着采样点数的不断增加，测量误差越来越大。其原因是：本文方法采用滑动递推的思想，减小了计算量，消除了冗余计算，实时性较高；采用矩形双窗并计及负频率的影响，减小了频谱泄露的影响，所以能始终保持较好的测量效果。

1—理论值；2—DTFT法；3—本文方法(加矩形双窗)

为了进一步考察本文所提方法的实际效果，利用本课题组所设计的科氏流量计实验平台进行实验验证。由于现有技术条件的限制，无法得到每点的实际相位差和时间差，可根据流量计的性能曲线，将实际流量换算成相应的时间差，以此作为时间差的理论参考值来估计相对误差。表1所示为不同流量下采用DTFT法和本文方法计算得到的时间差均值和相对误差。从表1可以看出：本文方法的相位差测量精度更高，计算结果更接近理论参考值，证实了本文方法的实用性和有效性。

表1 不同流量下的时间差均值及相对误差

3 结论

1) 采用矩形双窗、计及负频率影响以及滑动递推的思想，提出一种基于矩形双窗的滑动DTFT相位差测量算法。

2) 本文所提算法能更好地抑制频谱泄露的影响，在无噪声、有噪声和采样点数变化的影响下，均能始终保持较高的测量精度；应用于科氏流量计的相位差测量，同样能始终保持较好地测量效果，可适用于高精度的相位差测量应用场合。

[1] 张海涛, 涂亚庆. 基于DTFT的一种低频振动信号相位差测量新方法[J]. 振动工程学报, 2007, 20(2): 180−184.
ZHANG Haitao, TU Yaqing. A new phase difference measurement method for low-frequency vibration signals based on DTFT[J]. Journal of Vibration Engineering, 2007, 20(2): 180−184.

[2] 刘灿涛, 赵伟, 袁俊. 基于数字相关原理的相位差测量新方法[J]. 计量学报, 2002, 23(3): 219−223.
LIU Cantao, ZHAO Wei, YUAN Jun. A new method for phase difference measurement based on digital correlation theory[J]. Acta Metrologica Sinica, 2002, 23(3): 219−223.

[3] 郑胜峰, 陈素明, 狄金海, 等. 一种基于多重互相关的相位差测量方法[J]. 宇航计测技术, 2012, 32(1): 34−40.
ZHENG Shengfeng, CHEN Suming, DI Jinhai, et al. Phase difference measurement of sinusoidal signal based on multi-layer cross-correlation[J]. Journal of Astronautic Metrology and Measurement, 2012, 32(1): 34−40.

[4] 江亚群, 何怡刚. 基于加窗DFT的相位差高精度测量算法[J]. 电路与系统学报, 2005, 10(2): 112−116.
JIANG Yaqun, HE Yigang. New algorithm for high-accuracy phase difference measurement based on windowed DFT[J]. Journal of Circuits and Systems, 2005, 10(2): 112−116.

[5] 陈孔阳. 一种基于改进DFT算法的相位差测量研究[J]. 微计算机信息, 2012, 28(4): 142−144.
CHEN Kongyang. A research on phase difference measurement based on improved DFT algorithm[J]. Microcomputer Information, 2012, 28(4): 142−144.

[6] 张海涛, 涂亚庆. 计及负频率影响的科里奥利质量流量计信号处理方法[J]. 仪器仪表学报, 2007, 3(3): 539−544.
ZHANG Haitao, TU Yaqing. New signal processing method with negative frequency contribution for Coriolis mass flowmeter[J]. Chinese Journal of Scientific Instrument, 2007, 3(3): 539−544.

[7] 沈廷鳌, 涂亚庆, 张海涛, 等. 科氏流量计的时变信号处理方法[J]. 重庆大学学报, 2013, 36(4): 93−98, 109.
SHEN Tingao, TU Yaqing, ZHANG Haitao, et al. A time-varying signal processing method for Coriolis mass Flowmeter[J]. Journal of Chongqing University, 2013, 36(4): 93−98, 109.

[8] 毛育文, 涂亚庆, 张海涛, 等. 极低频信号的一种离散频谱校正新方法[J]. 振动工程学报, 2012, 25(4): 474−480.
MAO Yuwen, TU Yaqing, ZHANG Haitao, et al. A discrete spectrum correction method for ultra low frequency signals[J]. Journal of Vibration Engineering, 2012, 25(4): 474−480.

[9] 陈奎孚, 王建立, 张森文. 低频成分的频谱校正[J]. 振动工程学报, 2008, 21(1): 38−42.
CHEN Kuifu, WANG Jianwen, ZHANG Senwen. Correction of frequency spectrum for low frequency components[J]. Journal of Vibration Engineering, 2008, 21(1): 38−42.

[10] 向玲, 杨世锡, 唐贵基. 次同步谐振下机组轴系弯扭振动信号分析[J]. 振动、测试与诊断, 2011, 31(2): 233−236, 269.
XIANG Ling, YANG Shixi, TANG Guiji. Crankle vibration analysis for engines radices frequency synchronous syntony[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2): 233−236, 269.

[11] 张平, 张小栋. 证据熵在旋转机械故障诊断中的应用[J]. 振动、测试与诊断, 2010, 30(1): 55−58.
ZHANG Ping, ZHANG Xiaodong. Application of proof entropy in fault diagnosis of rotating machinery[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(1): 55−58.

[12] 易立强, 邝继顺, 欧阳雄. 基于一类新窗的高精度相位差测量方法[J]. 系统仿真学报, 2007, 19(23): 5543−5545.
YI Liqiang, KUANG Jishun, OUYANG Xiong. New accurate measurement method of phase difference based on double-windows[J]. Journal of System Simulation, 2007, 19(23): 5543−5545.

[13] SHEN Tingao, TU Yaqing, ZHANG Haitao. A novel method for CMF signal processing based on the revised sliding recursive DTFT algorithm[C]//2012 24th Chinese Control and Decision Conference. Taiyuan, China, 3323−3328.

New sliding DTFT algorithm for high-accuracy phase difference measurement based on double rectangle window

SHEN Tingao, TU Yaqing, ZHANG Haitao, LI Ming

(Department of Information Engineering, Logistical Engineering University, Chongqing 401311, China)

As the signals in vibration engineering domain have ultra low frequency or adjacent Nyquist frequency, there is large error in measuring it using traditional phase difference measurement. In order to obtain good inhibition of spectral leakage and high accuracy of phase difference measurement, a new sliding DTFT (discrete time Fourier transform) algorithm for high-accuracy phase difference measurement based on double rectangle window was presented, which is based on the traditional DTFT algorithm, combined with double rectangle window, negative frequency contribution and the idea of sliding recursive. It’s principle and achievement method were also expounded. The results show that the algorithm has less computation work and is easy to be realized. When it is applied in phase difference measurement, the measuring error caused by spectral leakage can be reduced, and the new method can obtain higher precision than conventional method of cosine window DTFT. Simulations and field tests verify the feasibility and effectiveness of the proposed method.

phase difference; discrete time Fourier transform (DTFT); cosine window; spectral leakage; negative frequency

TN911

A

1672−7207(2015)02−0554−07

2014−02−12；

2014−04−20

国家自然科学基金资助项目(61271449, 61302175)；重庆市自然科学基金资助项目(CSTC, 2011BA2015; CSTC, 2013jcyjA40030)(Projects (61271449, 61302175) supported by the National Natural Science Foundation of China; Projects (CSTC, 2011BA2015; CSTC, 2013jcyjA40030) supported by the Natural Science Foundation of Chongqing City)

涂亚庆，教授，从事智能检测与智能仪表研究；E-mail：yqtcq@sina.com

10.11817/j.issn.1672-7207.2015.02.025

(编辑 陈灿华)