一种邻域搜索的人工蜂群算法

周新宇，吴志健，邓长寿，彭虎



一种邻域搜索的人工蜂群算法

周新宇1, 2，吴志健1，邓长寿3，彭虎1

(1. 武汉大学 计算机学院，软件工程国家重点实验室，湖北 武汉，430072；2. 江西师范大学 计算机信息工程学院，江西 南昌，330022；3. 九江学院 信息科学与技术学院，江西 九江，332005)

提出采用邻域搜索机制来改进人工蜂群算法的解搜索方程，从当前食物源的环形邻域拓扑结构中选择较优的邻居食物源进行开采，平衡算法的勘探与开采能力。此外，为保存侦察蜂的搜索经验，提出采用一般反向学习策略生成被放弃食物源的反向解，提高算法的搜索效率。在20个典型的benchmark函数上验证算法的性能，并与6种知名的改进算法进行对比。实验结果表明：本文算法在收敛速度和解的精度上均有较大优势。

全局优化；人工蜂群；邻域搜索；一般反向学习

人工蜂群(artificial bee colony, ABC)算法是近年来提出的一种较为新颖的全局优化算法[1−2]，具有结构简单、控制参数少、易于实现等特点。该算法与粒子群优化(particle swarm optimization, PSO)算法[3]类似，都是通过模拟自然界生物的群体智能行为而设计的群智能优化算法。但与PSO算法不同的是，ABC模拟的是蜂群的智能采蜜行为，它根据不同种类蜜蜂的分工协作，实现整个蜂群采蜜量的最大化，即找到待优化问题的最优解[4]。Karaboga等[5]研究结果表明，ABC的性能要优于或者相当于差分演化(differential evolution，DE)算法、PSO算法和遗传算法。目前，ABC算法已成功地用于解决多种不同类型的实际优化问题，如参数优化[6]、符号回归[7]、神经网络[8−9]以及车辆路径问题[10]等。在标准ABC算法中，雇佣蜂(employed bee)和观察蜂(onlooker bee)共用一种解搜索方程(solution search equation)生成新的候选食物源，因而算法的性能主要依赖于该方程。然而，最近的研究[11−13]指出，这种解搜索方程侧重于算法的勘探(exploration)能力，而开采(exploitation)能力不足，易导致算法的收敛速度过慢和解的精度不高。针对此问题，受PSO算法的启发，Zhu等[11]提出了一种引导的ABC算法，在解搜索方程中融入全局最优解的信息，用于提高算法的开采能力。类似地，Banharnsakun等[12]也在全局最优解的基础上，提出了改进的解搜索方程。Gao等[13]受DE算法的“DE/best/1”变异策略的启发，提出了一种“ABC/best/1”的改进解搜索方程，在该方法中同样也利用了全局最优解。这几种改进的ABC算法均利用了全局最优解信息来提高算法的开采能力。虽然使用全局最优解可增强开采能力，但在一定程度上也易导致算法陷入局部最优，特别是在优化多峰函数时。因此，为提高ABC算法的开采能力且不易于陷入局部最优，受局部版本的粒子群优化(local particle swarm optimization, LPSO)算法[14−15]的启发，本文提出一种邻域搜索的ABC(neighborhood search based artificial bee colony, NSABC)算法。LPSO是标准PSO算法[16]的一个改进版本，它采用粒子所在邻域的最优粒子代替标准PSO的全局最优粒子来指导粒子的速度更新。受此启发，在观察蜂阶段，采用邻域搜索机制从当前食物源的环形邻域拓扑结构中选择1个最优的食物源，在该食物源的邻域范围内搜索新的候选食物源，有助于增强算法的开采能力且不易于陷入局部最优。此外，为帮助侦察蜂(scout bee)保存搜索经验，提出采用一般反向学习策略来生成被放弃食物源的反向解，使得侦察蜂可以快速地找到新的优秀食物源。为验证本文算法的性能，在20个典型的benchmark函数(包括单峰、多峰以及偏移加旋转类型)上开展数值实验，并与6种不同类型的改进算法进行对比。

1 人工蜂群算法

在ABC算法中，人工蜂群包含了3种不同类型的蜜蜂：雇佣蜂、观察蜂和侦察蜂。雇佣蜂负责勘探食物源，并在蜂巢的舞蹈区通过摇摆舞的形式将食物源的相关信息分享给观察蜂[17]，这些信息包括食物源的位置以及蜂蜜量。然后，观察蜂根据收到的信息以一定概率选择某一食物源继续开采，该食物源的蜂蜜量越多，被选中的概率就越高。若一个食物源被开采完，则相对应的雇佣蜂就转变为侦察蜂，再重新随机搜索一个新的食物源。值得说明的是：1个食物源的位置对应于待优化问题的1个候选解，食物源的蜂蜜量即指适应值；而雇佣蜂与食物源是一一对应的，同时雇佣蜂的数量和观察蜂相同。

类似于其他演化算法，ABC算法同样采用1个随机初始化的群体开始迭代搜索。设群体规模为，其中食物源X=(x,1, x,2, …, x,D)代表1个候选解，∈{1, 2, …,}，为待优化问题的维度。初始化之后，ABC算法根据蜜蜂的类型，将优化过程分为3个阶段。

1) 雇佣蜂阶段。在该阶段，每一只雇佣蜂在对应的食物源X处，采用解搜索方程生成1个新的食物源V=(v,1，v,2，…，v,D)。若V的蜂蜜量更多即适应值更优，则就替换X。该方程如下：

2) 观察蜂阶段。在所有雇佣蜂完成了勘探后，观察蜂根据接收到的信息随机选择一个食物源进一步开采。这种选择方式通常采用基于适应值的方法，如：轮盘赌机制。若观察蜂采用轮盘赌机制进行选择，则食物源X被选中的概率p为

其中：f为食物源X的适应值。从式(2)可以看出，食物源的适应值越大，被观察蜂选中的概率越高。

3) 侦察蜂阶段。当雇佣蜂对应的食物源的适应值连续次未更新，说明该食物源已被开采耗尽。这种情况下，雇佣蜂转变成侦察蜂，采用式(2)重新随机搜索1个新的食物源。

其中：rand(0,1)为[0, 1]间的随机数；[a,b]为第维变量的上下界。值得说明的是，除群体规模等公共参数外，是ABC算法中唯一的参数。

2 基于邻域搜索的ABC算法

2.1 邻域搜索机制

PSO算法模拟的是鸟群和鱼群的觅食行为[16]。在标准PSO算法中，粒子的速度更新受自身历史经验和群体历史经验的共同影响，如式(4)所示：

但Kennedy等[14−15]指出：标准PSO算法中的在求解多峰函数时易出现早熟现象，为此提出了一种局部版本的PSO算法，即LPSO算法。在LPSO算法中，粒子的速度更新受自身历史经验和邻域的最优粒子的共同影响，即

受LPSO算法的启发，本文提出在观察蜂阶段采用邻域搜索机制来选择食物源进行开采，而不是直接利用全局最优解的信息。因而，在求解多峰函数时，能够利用邻域内较优的个体信息，而非全局最优解信息，有利于增加群体的多样性，避免算法陷入局部最优。此外，雇佣蜂阶段则保持原来的解搜索方程不变，这样有助于结合雇佣蜂的勘探能力和观察蜂的开采能力，充好利用和保持这两种能力的平衡，提高ABC的搜索性能。因此，对观察蜂而言，新食物源的搜索方式如下：

其中：()为当前食物源X所处邻域的最优食物源，设邻域半径为，则()∈{−，…，−1，，1，…，}。1∈{1，2，…，}，2∈{−，…，−1，，1，…，}，且满足1，2和互不相等.

值得说明的是，邻域搜索的方式与群体的拓扑结构类型是相关的，依据Das等[18]的建议，本文采用效率较高的环形邻域拓扑结构。这种结构的特点是群体中个体是否相邻是由下标的关系确定，而不是搜索空间中的欧式距离。图1给出了式(6)采用的环形邻域拓扑结构示意图，其中为邻域半径。

图1 环形邻域拓扑结构

为更加直观地说明提出的邻域搜索机制与原解搜索方程的区别，以2维Shekel’s Foxholes函数为例，采用标准ABC算法和结合了邻域搜索机制的ABC(简记为ABC-NS)分别优化该函数，给出2种算法在不同演化代数下的群体分布情况。2维的Shekel’s Foxholes函数是多峰函数，有24个局部极值和1个全局极值(−32,−32)=0.998 004，搜索空间的边界是[65.536, 65.536]2。该函数的具体定义可参考文献[19]，图2所示为该函数的3-D图。对标准ABC算法和ABC-NS算法，采用相同的参数设置，=30，=100。而在ABC-NS算法中，按文献[18]的建议，取邻域半径为群体规模的10%。

图2 2维Shekel’s Foxholes函数的3-D图

图3所示为标准ABC和ABC-NS算法在演化过程中的第1代、第15代和第30代的群体分布情况，实心圆点表示食物源，空心矩形是Shekel’s Foxholes函数在平面上的投影，即25个极值点。从图3可以看出，在第1代中由于随机初始化的作用，2种算法的群体分布无明显区别，均随机分散在搜索区域中。但随着演化代数的增加，2种算法的有效搜索区域都不断收缩，食物源也向各个极值点靠拢。但值得注意的是，ABC-NS算法的收缩速度要明显比ABC算法的快。特别地，在第30代时，ABC-NS算法的所有食物源都已收敛到全局极值点处，而ABC算法只有部分食物源到了该点。结果表明：采用邻域搜索机制可以有效地利用邻域中优良个体的信息，增强算法的开采能力，且不易于陷入局部最优。

(a) ABC算法在第1代；(b) ABC算法在第15代；(c) ABC算法在第30代；(d) ABC-NS算法在第1代；(e) ABC-NS算法在第15代；(f) ABC-NS算法在第30代

2.2 一般反向学习策略

在标准ABC算法的侦察蜂阶段，一个食物源若超过次未更新，则认为该食物源被开采耗尽，对应的雇佣蜂转变为侦察蜂，并采用式(3)再重新随机搜索一个新的食物源。这种机制存在不足，即被放弃的食物源可能包含了有益的搜索信息，直接采用随机生成的新食物源来替换，则易导致这部分信息丢失。为此，本文提出采用一般反向学习策略生成被放弃食物源的反向解，充分利用这些食物源所含的有益信息，为侦察蜂提供更多的搜索经验，有助于进一步提高算法的搜索效率。

一般反向学习(generalized opposition-based learning, GOBL)策略是反向学习[20−21]的改进版本。它的主要思想是：对当前待优化问题的1个可行解，同时计算并评估其反向解，从中选择较优的作为候选解。该方法能提高找到全局最优解的概率，文献[22]验证了GOBL策略的有效性。

设X=(x,1，x,2，…，x,D)是当前待优化问题的一个可行解，其对应的反向解可定义为

其中：x,j∈[a,b]，∈(0,1)为一般化系数，[da, db]为第维搜索空间的动态边界，可按如下公式计算得到：

若反向解跳出边界[a,b]成为非可行解，对其采用随机生成的方法来重置：

其中：rand(∙)是区间[a,b]上的一个随机数。

除了生成被放弃食物源的反向解，依旧使用原机制即式(3)生成1个随机食物源，从反向解与随机食物源中选择较优的1个作为新的食物源。该过程可以表示为

2.3 NSABC的伪代码描述

本文提出的NSABC算法在标准ABC的基础上做了2处改进，1) 在观察蜂阶段，采用邻域搜索机制来增强解搜索方程的开采能力；2) 在侦察蜂阶段，采用一般反向学习策略来生成被放弃食物源的反向解用于保存搜索经验。Algorithm 1中给出NSABC的伪代码，其中表示适应度函数的评估次数，Max为适应度函数的最大评估次数，trial记录了食物源X的适应值未更新的次数。

算法1 Pseudocode of NSABC

Randomly generatefood sources {X|=1，2，…，};

=;

while≤ Maxdo

/* Employed bee phase */

for1todo

Generate a new candidate solutionVaccording to Eq. (1);

if(V) <(X) then

ReplaceXwithV;

trial= 0;

else

trial=trial+1;

end

=+1;

end

/* Onlooker bee phase */

Calculate the probabilitypaccording to Eq. (2);

for1todo

Choose a food sourceXfrom the current populationby the roulette wheel selection mechanism;

Generate a new candidate solutionVaccording to Eq. (6);

if(V) <(X) then

ReplaceXwithV;

trial= 0;

else

trial=trial+1;

end

=+1;

end

/* Scout bee phase */

for1todo

iftrial>then

trial= 0;

Generate the opposite solution ofX,, by Eq. (7);

Generate a new random food sourceVaccording to Eq. (3);

Pick out the better one fromandVforXaccording to Eq. (10);

=+2;

end

end

end

3 数值实验及分析

3.1 Benchmark函数

为验证NSABC算法的性能，采用20个典型的benchmark函数进行实验，如表1所示。F01-F04是单峰函数，F05在维度大于3时为多峰函数[23]。F06是非连续的函数，F07是带噪声的函数。F08-F13是多峰函数，而F14-F20是带偏移和旋转的复杂多峰函数。函数F01~F13的具体定义见参考文献[18]，F14~F20的具体定义见参考文献[24]。

表1 实验中使用的benchmark函数

3.2 策略有效性分析

为验证NSABC采用的2种策略的有效性，分别设计了2种算法ABC-NS和ABC-GOBL进行对比分析。ABC-NS算法是在标准ABC的基础上，仅在观察蜂阶段采用邻域搜索机制，其他部分保持不变；而ABC-GOBL算法是在标准ABC算法的基础上，仅在侦察蜂阶段采用一般反向学习策略，其他部分保持不变。因此，实验中共包含(标准ABC，ABC-NS，ABC-GOBL和NSABC) 4种算法的比较，4种算法采用相同的参数设置，=30，=100。而对ABC-NS和NSABC算法，则按文献[18]的建议，设置邻域半径=10%∙。函数的维度为=30，适应度函数的最大评估次数Max按文献[24]的建议设置为：对函数F01~F13，Max=5 000；对函数F14~F20，Max= 10 000。实验中，每种算法在每个函数上独立运行30次，记录结果的均值与方差。表2给出了4种算法的结果，其中均值由()−(X)得到，*为全局极值点。

表2　D=30时标准ABC，ABC-NS，ABC-GOBL和NSABC算法的结果

从表2可以看出：与ABC算法相比，ABC-NS算法在大部分函数上的结果更好，仅在函数F03和F20上略差，这说明邻域搜索机制有助于增强ABC算法的性能。ABC算法仅在函数F01和F03上比ABC-GOBL算法略优，而在其他函数上ABC-GOBL算法更好，这说明采用GOBL策略是有效的。结合2种策略，NSABC算法取得了4种算法中的最好结果，在所有测试函数上的性能均比ABC算法更优或者相当。值得说明的是，NSABC算法在函数F03，F04和F10上的性能比单独使用1种策略更优，这说明2种策略的结合能够取得更好的效果。

为了在统计意义上比较4种算法的性能，采用了非参数的Friedman检验[25−26]统计4种算法的平均排名情况。表3给出了4种算法的平均排名情况。从表3可看出：NSABC算法的性能最优，而其他3种算法性能从优到劣依次为：ABC-NS，ABC-GOBL和ABC算法。

表3 标准ABC，ABC-NS，ABC-GOBL和NSABC算法的平均排名

3.3 与其他改进ABC算法的比较

将NSABC算法与其他3种知名的改进ABC算法GABC[11]，MABC[13]和GOABC算法[27]进行对比研究。GABC算法是引导的ABC算法，它受PSO算法的启发，将全局最优解的信息融入到解搜索方程中，用于提高ABC算法的开采能力。MABC算法提出了类似于DE算法中的“DE/best/1”变异策略的解搜索方程，在全局最优解的邻域内搜索新的食物源，实验结果表明：该算法能够有效地增强ABC的搜索性能。GOABC算法是基于一般反向学习策略的ABC算法，它在算法的迭代过程中生成整个群体的反向解，从当前群体和反向群体中选择较优的个体进入下一代，这种机制与其他基于反向学习策略的算法是相同的，如反向学习的DE算法(ODE)[21]。然而，不同于GOABC的是，本文提出的NSABC只是在侦察蜂阶段对被放弃的食物源生成反向解。

4种算法的公共参数设置为=30，=100；对函数F01~F13，Max=5 000；而对函数F14~F20，Max=10 000。对每个算法的特殊参数按原文献进行设置，对GABC算法，=1.5；对MABC算法，=0.7；对GOABC算法，=0.3。实验中对所有函数进行2种维度的实验，分别取=30和=50。此外，为了在统计意义上比较2个算法的性能是否存在显著性差异，按文献[25−26]采用非参数Wilcoxon假设检验进行统计，显著性水平=0.05。表4和表5分别给出了=30和=50时4种算法的结果，其中，符号“+”、“−”和“≈”分别表示NSABC的性能要优于、劣于和相当于对比算法。

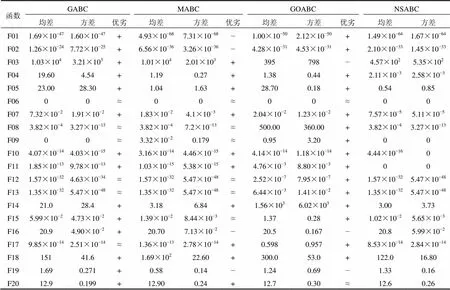
表4　D=30时 GABC,MABC,GOABC和NSABC算法的结果

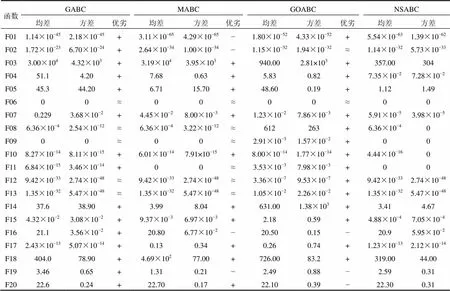
表5　D=50时 GABC、MABC、GOABC和NSABC算法的结果

从表4可看出：NSABC在大部分函数上要优于其他3种对比算法。具体来说，NSABC算法在所有函数上要优于或者相当于GABC算法。与MABC算法相比，NSABC算法在4个函数上的性能不如MABC算法，例如在函数F01上。函数F01是简单的球状单峰函数，通常一个开采能力更强的算法会取得更优的结果。MABC算法是在全局最优解的邻域内搜索新的食物源，因而其开采能力非常强，所以，在该函数上取得了不错的效果。但在多峰函数上，NSABC算法的性能更好。值得注意的是：在函数F09上，虽然MABC算法的均值比NSABC算法要差得多，但Wilcoxon检验的结果却是两者无显著性差异的。出现这种情况的可能原因是：MABC算法在F09上的30次运行结果并不是每次都能得到最优值0，而是产生了噪声，即偶尔出现较差的结果，这也反映了NSABC算法的鲁棒性更好。与GOABC算法相比，NSABC算法在15个函数上更优。

从表5可以看出：与=30时类似，NSABC算法依然在大部分函数上要优于其他3种算法。虽然随着维度增加，求解的难度也相应增加，但NSABC算法的性能表现良好。表6给出了这4种算法在=30和=50时的平均排名。从表6可得：NSABC算法在2种测试维度下均取得了最好的排名。此外，图4给出了=30时这4种算法在部分函数上的收敛曲线。从图4可看出：NSABC算法的收敛速度较快。值得注意的是，MABC算法也具有较快的收敛速度。

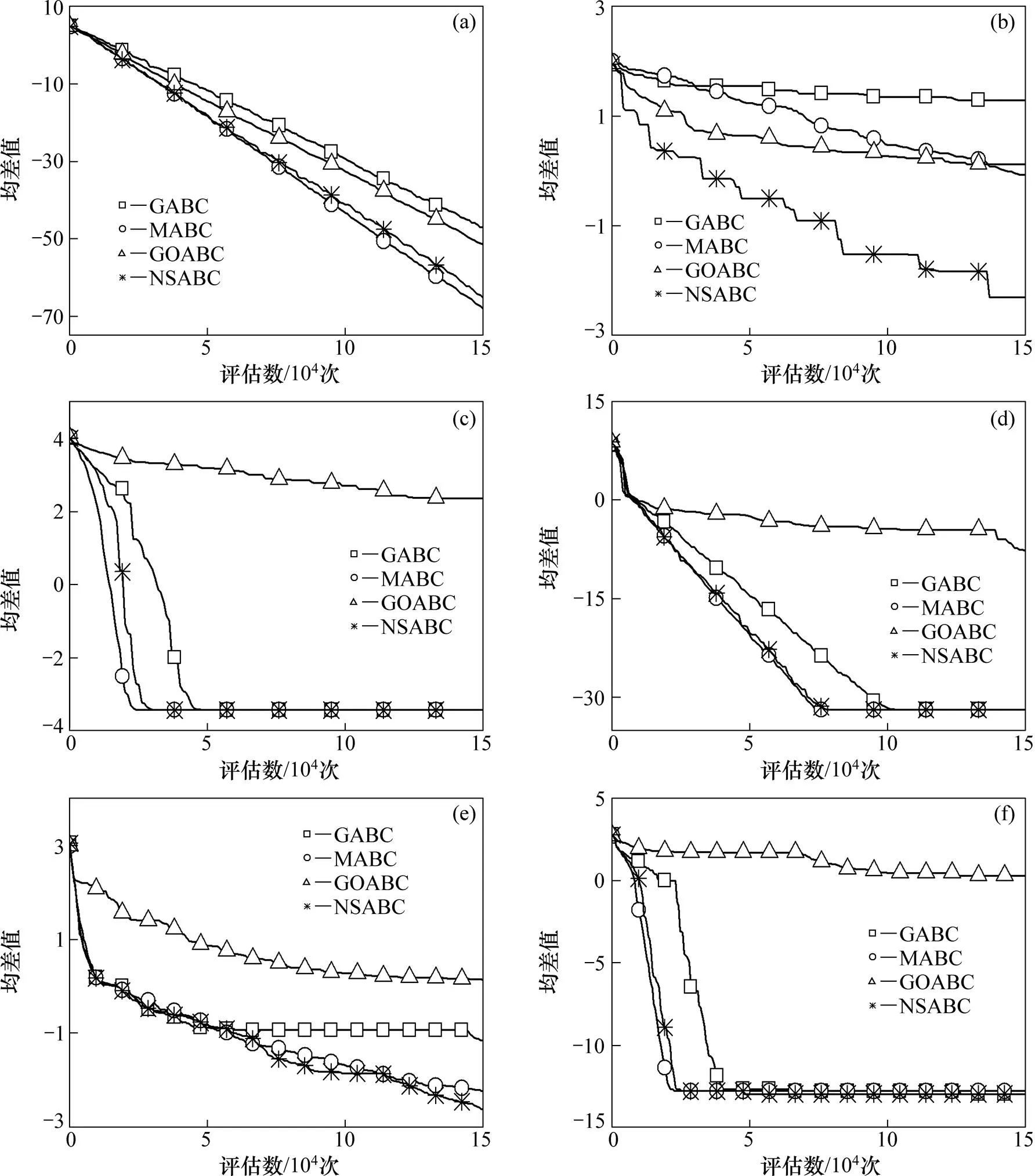
(a) F01；(b) F04；(c) F08；(d) F12；(e) F15；(f) F17

表6 GABC，MABC，GOABC和NSABC算法的平均排名

3.4 与其他相关演化算法的比较

为进一步评估NSABC的性能，将其与另外3种知名的相关演化算法(LPSO[14]，GOPSO[22]和DEGL/SAW算法[18])进行对比。LPSO算法是局部版本的PSO算法，采用了邻域搜索机制。GOPSO算法是采用一般反向学习策略的PSO算法，它以一定概率生成群体中所有粒子的反向解，从当前解和反向解中选择较优的个体进入下一代。DEGL/SAW算法结合了邻域搜索策略的DE算法，该算法同样采用了环形邻域拓扑结构。这3种算法的参数全部采用原文献的推荐设置，如表7所示。

表7 LPSO, GOPSO和DEGL/SAW算法的参数设置

注：为群体规模；为惯性系数；1和2为学习因素；为反向学习概率；为缩放因子；为交叉概率。

所有函数的维度设为=30，适应度函数最大评估次数与3.3节中的相同。表8所示为这4种算法的最终结果。从表8可看出：NSABC算法的总体性能要显著优于对比算法。具体地，与LPSO算法和GOPSO算法相比，NSABC算法在17个函数上取得了更好的结果。与DEGL/SAW算法相比，NSABC算法在12个函数上更优。值得注意的是，在函数F05上，DEGL/SAW算法的结果要明显优于其他3种算法。文献[23]指出F05在三维以上属于多峰函数，其全局极值位于一个狭长的、抛物线状的扁平山谷中，对大多算法而言很难进入到这个山谷中。但在函数F11上，NSABC算法的结果比其他3种算法明显更优。表9所示为采用非参数Friedman检验得到的平均排名。从表9可以看出：NSABC算法的整体性能最好。图5所示为这4种算法在部分函数上的收敛曲线。

表8 D=30时 LPSO，GOPSO，DEGL/SAW和NSABC算法的结果

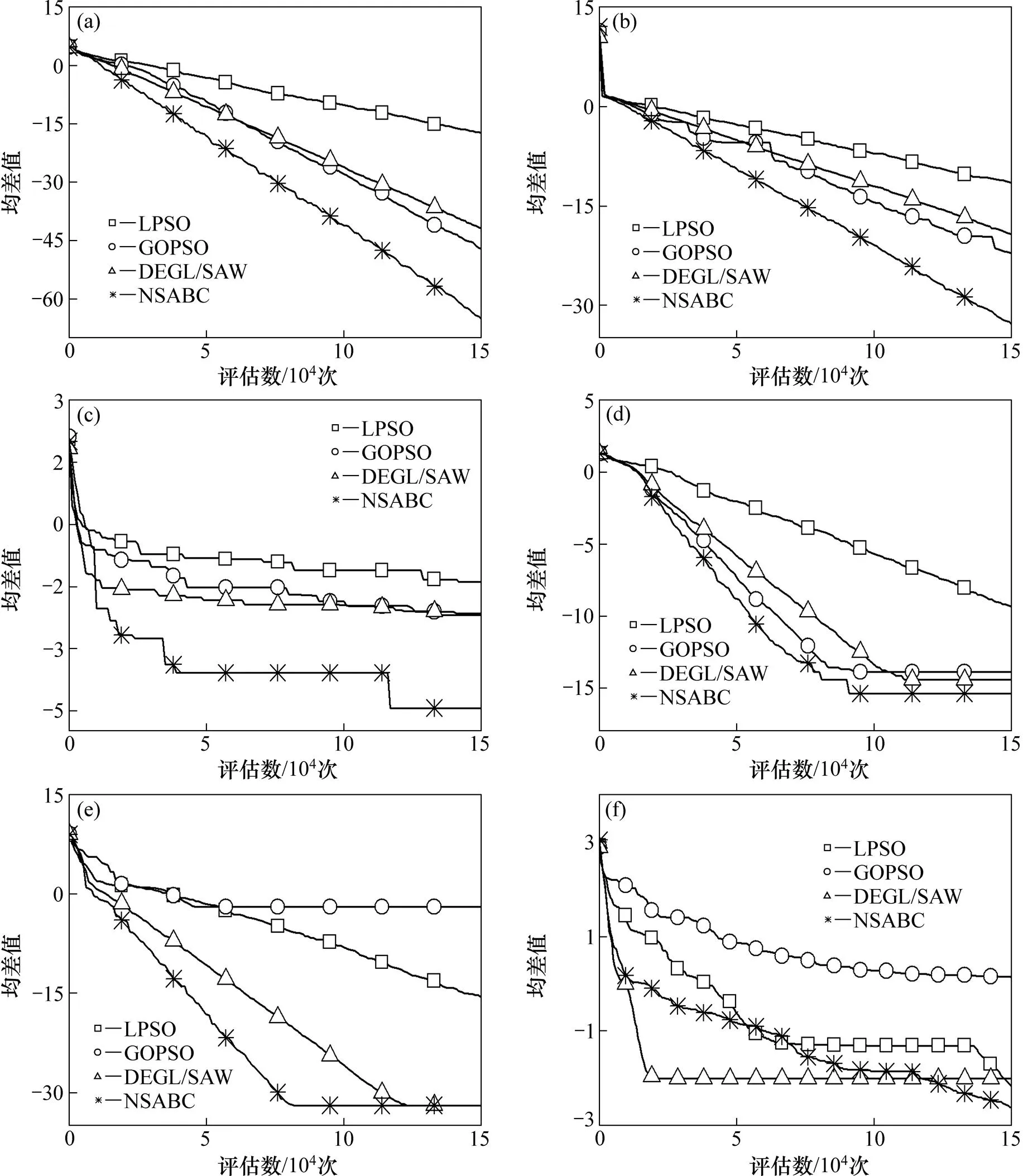
(a) F01；(b) F02；(c) F07；(d) F10；(e) F13；(f) F15

表9 LPSO，GOPSO，DEGL/SAW和NSABC算法的平均排名

3.5 运行时间比较

通常，演化算法的运行时间包含算法的操作算子的运行时间和评估适应度函数的时间。将标准ABC和NSABC算法在本文采用的20个benchmark函数上分别独立运行30次，记录消耗的平均CPU时间。2种算法的公共参数采用相同的设置，=30，= 100。适应度函数的最大评估次数Max与前面相同，测试函数的维度设为30和50。算法的运行平台如下：操作系统为Windows 7 (x64)，CPU为Intel Core 2 Quad CPU Q8200 (2.33 GHz)，内存为4G，编程语言及运行环境为Java和Eclipse SDK 4.2.0。标准ABC和NSABC算法的平均CPU时间如表10所示。从表10可以看出：在=30时，NSABC与标准ABC的CPU时间之比的范围为[0.85, 1.24]，总的时间比是1.05。值得注意的是，在4个函数上的CPU时间之比要低于1，说明NSABC的运行时间比标准ABC算法的要低。出现这种现象的可能原因是在NSABC算法中，对所有连续次未更新的食物源均采用了一般反向学习机制来寻找新的替代食物源，使得侦察蜂阶段消耗了更多的适应度函数评估次数，减少了雇佣蜂和跟随蜂阶段的执行次数，从而降低了整个算法的运行时间。当维度从30增至50时，函数的复杂度也随之增加，从而导致算法的运行时间也相应增加。但对NSABC算法而言，其与标准ABC的CPU时间之比从30维时的1.05降至50维时的1.00，这正说明了适应度函数的复杂度越高，算法的操作算子占整个运行时间的比例越小。总之，与标准ABC算法相比，NSABC算法的运行时间未明显地增加。

表10 标准ABC和NSABC算法的平均CPU时间

4 结论

1) 为提高ABC算法的开采能力，受局部版本的PSO算法的启发，提出采用邻域搜索机制来改进解搜索方程。此外，为保存搜索经验，提出采用一般反向学习策略来生成被放弃食物源的反向解。

2) 在20个典型的benchmark函数上验证提出算法的性能，并将实验结果与6种知名的改进算法进行对比，结果表明这2种策略能够有效地提高ABC算法的性能，在收敛速度和解的精度上均有较大的优势。

3) 下一步研究工作的重点是将本文算法应用于求解实际优化问题，如分布式软件系统的部件部署 问题。

[1] Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri: Erciyes University, 2005.

[2] Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459−471.

[3] 余伶俐, 蔡自兴. 改进混合离散粒子群的多种优化策略算法[J]. 中南大学学报(自然科学版), 2009, 40(4): 1047−1053.
YU Lingli, CAI Zixing. Multiple optimization strategies for improving hybrid discrete particle swarm [J]. Journal of Central South University (Science and Technology), 2009, 40(4): 1047−1053.

[4] 高卫峰, 刘三阳, 黄玲玲. 受启发的人工蜂群算法在全局优化问题中的应用[J]. 电子学报, 2012, 40(12): 2396−2403.
GAO Weifeng, LIU Sanyang, HUANG Lingling. Inspired artificial bee colony algorithm for global optimization problems[J]. Acta Electronic Sinica, 2012, 40(12): 2396−2403.

[5] Karaboga D, Akay B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108−132.

[6] 贾宗圣, 司锡才, 王桐. 基于人工蜂群技术的海杂波参数优化方法[J]. 中南大学学报(自然科学版), 2012, 43(9): 3485−3489.
JIA Zongsheng, SI Xicai, WANG Tong. Optimum method for sea clutter parameter based on artificial bee colony[J]. Journal of Central South University (Science and Technology), 2012, 43(9): 3485−3489.

[7] Karaboga D, Ozturk C, Karaboga N, et al. Artificial bee colony programming for symbolic regression[J]. Information Sciences, 2012, 209(11): 1−15.

[8] Yeh W C, Hsieh T J. Artificial bee colony algorithm-neural networks for s-system models of biochemical networks approximation[J]. Neural Computing and Applications, 2012, 21(2): 365−375.

[9] Garro B A, Sossa H, Vazquez A R. Artificial neural network synthesis by means of artificial bee colony (ABC) algorithm[C]//Proceedings of the IEEE Congress on Evolutionary Computation. New Orleans: IEEE, 2011: 331−338.

[10] Szeto W, Wu Y, Ho S C. An artificial bee colony algorithm for the capacitated vehicle routing problem[J]. European Journal of Operational Research, 2011, 215 (1): 126−135.

[11] Zhu G, Kwong S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166−3173.

[12] Banharnsakun A, Achalakul T, Sirinaovakul B. The best-so-far selection in Artificial Bee Colony algorithm[J]. Applied Soft Computing, 2011, 11(2): 2888−2901.

[13] Gao W F, Liu S Y. A modified artificial bee colony algorithm[J]. Computers & Operations Research, 2012, 39(3): 687−697.

[14] Kennedy J, Mendes R. Population structure and particle swarm performance[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Honolulu: IEEE, 2002: 1671−1676.

[15] Kennedy J, Mendes R. Neighborhood topologies in fully informed and best-of-neighborhood particle swarms[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2006, 36(4): 515−519.

[16] Shi Y, Eberhart R. A modified particle swarm optimizer[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Anchorage A.K.: IEEE, 1998: 69−73.

[17] Karaboga D, Gorkemli B, Ozturk C, et al. A comprehensive survey: artificial bee colony (ABC) algorithm and applications[J]. Artificial Intelligence Review, 2012, 39(3): 1−37.

[18] Das S, Abraham A, Chakraborty U K, et al. Differential evolution using a neighborhood-based mutation operator[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(3): 526−553.

[19] Yao X, Liu Y, Lin G. Evolutionary programming made faster[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82−102.

[20] Rahnamayan S, Tizhoosh H R, Salama M M A. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64−79.

[21] 周新宇, 吴志健, 王晖, 等. 一种精英反向学习的粒子群优化算法[J]. 电子学报, 2013, 41(8): 1647−1652.
ZHOU Xinyu, WU Zhijian, WANG Hui, et al. Elite opposition-based particle swarm optimization[J]. Acta Electronic Sinica, 2013, 41(8): 1647−1652.

[22] Wang H, Wu Z J, Rahnamayan S, et al. Enhancing particle swarm optimization using generalized opposition-based learning[J]. Information Sciences, 2011, 181(20): 4699−4714.

[23] Shang Y W, Y. H. Qiu. A note on the extended Rosenbrock function[J]. Evolutionary Computation, 2006, 14(1): 119−126.

[24] Suganthan P N, Hansen N, Liang J J, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[R]. Singapore: Nanyang Technological University, 2005.

[25] Garcia S, Molina D, Lozano M, et al. A study on the use of non-parametric tests for analyzing the evolutionary algorithms' behavior: a case study on the CEC'2005 Special Session on Real Parameter Optimization[J]. Journal of Heuristics, 2009, 15(6): 617−644.

[26] Garcia S, Molina D, Lozano M, et al. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power[J]. Information Sciences, 2010, 180(10): 2044−2064.

[27] El-Abd M. Generalized opposition-based artificial bee colony algorithm[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Brisbane: IEEE, 2012: 1−4.

Neighborhood search-based artificial bee colony algorithm

ZHOU Xinyu1, 2, WU Zhijian1, DENG Changshou3, PENG Hu1

(1. State Key Laboratory of Software Engineering, Computer School, Wuhan University, Wuhan 430072, China;2. College of Computer and Information Engineering, Jiangxi Normal University, Nanchang 330022, China;3. School of Information Science & Technology, Jiujiang University, Jiujiang 332005, China)

The neighborhood search mechanism was introduced to improve the solution search equation of artificial bee colony algorithm. In the ring neighborhood topology of current food source, the exploitation was focused on the best neighbor food source to balance the capabilities of exploration and exploitation. Moreover, in order to preserve search experience for scout bees, the generalized opposition-based learning strategy was utilized to generate opposite solutions of the discarded food sources, which helps enhance the search efficiency. Twenty classic benchmark functions were used to test the performance of our approach, and then the experimental results were compared with other six well-known algorithms. The results show that our approach has better convergence speed and solution accuracy.

global optimization; artificial bee colony; neighborhood search; generalized opposition-based learning

TP301.6

A

1672−7207(2015)02−0534−13

2014−03−25；

2014−06−26

国家自然科学基金资助项目(61364025, 61305150, 61462045)；中央高校基本科研业务费专项资金资助项目(2012211020205)；软件工程国家重点实验室开放基金资助项目(SKLSE2014-10-04)(Projects (61364025, 61305150, 61462045) supported by the National Natural Science Foundation of China; Project (2012211020205) supported by the Fundamental Research Funds for the Central Universities; Project (SKLSE2014-10-04) supported by the Foundation of State Key Laboratory of Software Engineering)

周新宇，博士，讲师，从事智能计算、并行计算研究；E-mail：xyzhou@whu.edu.cn

10.11817/j.issn.1672-7207.2015.02.023

(编辑 赵俊)