带楼板钢筋混凝土T形梁火灾下(后)温度场研究

王卫华，董毓利



带楼板钢筋混凝土T形梁火灾下(后)温度场研究

王卫华，董毓利

(华侨大学 土木工程学院，福建 厦门，361021)

为了进一步研究ISO-834标准火灾作用下三面受火带楼板钢筋混凝土T形梁的温度场分布，采用ABAQUS非线性有限元软件建立带楼板钢筋混凝土T形梁的温度场分析模型，在此基础上，在不同T形梁截面尺寸和高宽比等情况下，对考虑升、降温全过程的温度场和火灾后温度场分布进行研究。研究结果表明：楼板对钢筋混凝土梁的截面升温有较大影响，T梁腹板宽度影响相邻楼板的温度场分布；考虑升温和降温全过程后，内部混凝土达到最高温度的时间明显滞后，距离受火面越远，升温滞后越严重；火灾后的混凝土截面温度场分布与升温或降温过程中任一时刻的温度场有较大不同，进行火灾后钢筋混凝土T形梁的力学性能分析时，应采用火灾后(历史最高)温度场。

钢筋混凝土；T形梁；楼板；温度场；有限元分析

随着城市规模的不断扩大，人口趋于集中，由于安全疏忽、线路老化、操作不规范等原因，火灾时有发生，给人民生命安全或财产带来较大损失。温度场分析是开展钢筋混凝土结构耐火性能或火灾后力学性能分析的前提基础，温度场计算结果会对钢筋混凝土结构的火灾下或火灾后力学性能产生较大影响。钢筋混凝土截面在受火过程中的温度场分布随受火时间而发生变化，故受火构件温度场分布一般按非稳定温度场来处理[1−2]。文献[3−5]采用时间空间递推等数值方法编制了钢筋混凝土梁板截面温度场的计算程序，并对截面温度场计算结果进行了分析。文献[6−8]开展了火灾下钢筋混凝土梁板构件截面的温度场试验研究，获得了火灾作用下钢筋混凝土梁板截面的温度场分布规律，数值分析结果与试验结果吻合较好，为后续的钢筋混凝土火灾下或火灾后的力学性能分析奠定了基础。文献[9]提出了一种钢筋混凝土构件方(矩)形截面温度场的简化计算方法。文献[10]利用热−力耦合模型开展了火灾下钢筋混凝土梁的三维数值分析。文献[11]在自然冷却、水冷却和炉温冷却3种情况下，对膨胀珍珠岩和浮石骨料混凝土的剩余承载力进行了研究，结果表明水冷却时高温后混凝土的剩余承载力最低，自然冷却时的剩余承载力最高。上述研究多为火灾下钢筋混凝土结构温度场分布或耐火性能的研究，而关于包含升温和降温过程钢筋混凝土截面温度场分布特点的研究较少，尤其是火灾后钢筋混凝土截面历史最高温度分布相关的研究较少。本文作者对三面受火带楼板钢筋混凝土T形梁在ISO-834标准升温曲线作用下的温度场试验研究，在此基础上进行包含升温和降温过程以及火灾后历史最高温度场的研究，以便揭示不同受火阶段下带楼板钢筋混凝土T形梁截面的温度场分布规律，为进一步开展温度相关的力学性能分析打下基础。

1 温度场分析中的传热方式

在温度场分析中，主要有3种传热方式[1]：1) 热传导，遵循傅里叶定律，热传导系数与物体自身的材料属性有关。对于普通混凝土材料，混凝土的骨料类型(硅质或钙质)和水分含量对热传导系数的影响较 大[12]。2) 热对流，可用牛顿冷却方程来描述。文献[13]建议对流换热系数主要与火灾类型有关，可按如下方法选取：ISO-834标准火灾取25 W/(m2∙K)、自然火灾模型取30 W/(m2∙K)；对于构件未受火面的对流换热系数取4 W/(m2∙K)，综合考虑辐射传热与对流传热，对流换热系数可取为9 W/(m2∙K)。3) 热辐射，基本定律遵循斯蒂芬−玻耳兹曼定律[1]。火灾中的热辐射过程较为复杂，与较多因素相关，如辐射面的相对位置、隐蔽程度、混凝土表面状况(粗糙度和颜色)和热力学温度等。在进行温度场分析时，综合辐射系数一般取0.5，文献[14]建议在无防火保护的钢构件温度场计算时，综合辐射系数取0.3~0.7(完全处在火中取0.7，离火源较远时取0.3)。

在实际火灾中，上述3种传热方式很少会单独发生。一种传热方式几乎不影响其他的传热方式，但是一种方式传热所导致目标物体的温度改变会改变其他传热方式热量的传递率，不能把多种传热方式引起的目标物体的温度简单相加，计算时应考虑这种作用结果的相互耦合作用，文献[12]采用综合传热系数考虑火焰与混凝土之间的热对流和热辐射，把火焰热流传递给柱表面的热流密度表示为

式中：1为综合考虑对流和辐射之后的综合换热系数。若采用综合换热系数，则不必单独考虑高温辐射对热传递过程的影响，否则，需要分别考虑对流和辐射在热传递过程中的作用。

2 材料热工参数

材料的热工参数是求解温度场的重要前提之一，传热分析所需材料参数为钢筋和混凝土的导热系数、比热容、密度等。文献[15−17]等提出了钢筋与混凝土的材料热工参数，温度场计算结果与试验实测结果吻合较好。

2.1 混凝土的导热系数

混凝土导热系数主要取决于其骨料类型和含水率，当温度小于 100 ℃时，含水率对热传导系数的影响比较明显，当温度大于100 ℃时，混凝土自由水不断蒸发，其影响变得越来越小。由于空隙中自由水分布和受热时水分迁移的复杂性，一般忽略含水率对混凝土热传导系数的影响。文献[12]给出的钙质混凝土的热传导系数如下：

式中：s为热传导系数，W/(m∙℃)；为温度。

2.2 混凝土的比热容(c)和容重(c)

混凝土在受高温加热后，其所含物质将发生态变反应，将发生与此相关的吸热与放热现象。混凝土的比热容受各组成成分影响较大，主要有混凝土的骨料类型、配合比和水分等的影响。随着温度升高，混凝土比热容缓慢增大，当温度升至500~600 ℃时，Ca(OH)2大量分解，硅质骨料中的石英由型转化为型，同时产生较大的热容波动。混凝土材料发生结晶水脱水的同时伴随复杂的物质化学变化过程，此时热传导分析中影响温度升高的主要因素为混凝土比热容发生突变[18]。由于水分蒸发，混凝土的容重(c)在温度升高以后有所降低，普通混凝土比轻骨料混凝土的容重损失小。计算时，通常把普通混凝土的容重视为常数。可以把钙质骨料混凝土的比热容(c)和容重(c)放在一起给出与温度的关系[12]。

在火灾条件下，温度升高至100 ℃附近时混凝土中的自由水开始蒸发，升温产生延迟。由于高温下混凝土内部自由水分的迁移过程比较复杂，参考文献[19]所述水蒸汽对混凝土比热容的影响，假定混凝土中所含水分占总质量的5%，对混凝土的比热容公式进行如下修改：

钢筋材料的热工参数采用文献[12]所推荐模型获得。

3 试验验证

进行了4榀带楼板钢筋混凝土T形梁-钢管混凝土柱框架(CFRC-1~CFRC-4)在ISO-834标准升温曲线作用下的温度场试验研究，试件参数如表1所示。为了验证上述材料热工参数和热分析参数选取的合理性，选取钢筋混凝土T形梁跨中截面的温度场分布进行研究。混凝土设计强度为C40，28 d立方体抗压强度为cu=47.4 MPa。截面尺寸和配筋如图1(a)所示。受火时，T形梁、板内温度由预埋在设定位置的铠装热电偶记录，温度测点布置如图1(b)所示。图1(c)所示为受火后带楼板钢筋混凝土T形梁的侧面外观，与受火前相比，混凝土颜色显著发白。

表1 试件参数

(a) T形梁截面尺寸及配筋(单位：mm)；(b)温度测点；(c) 受火后的侧面

建立钢管混凝土柱−钢筋混凝土梁框架温度场的有限元计算模型，核心混凝土、混凝土楼板和底梁采用热传导的三维实体单元DC3D8，钢筋采用Truss单元DC1D2，模型网格划分采用6面体的结构网格划分。采用ABAQUS软件的热传导模块进行计算时，需要在所建模型的属性设置中设置相应的斯忒芬−波尔兹曼(5.67×10−8W/(m2×K4))常数和温度(−273 ℃)。由于嵌入(Embedded)只能产生6个力学自由度上的约束关系而不能实现温度自由度(NT11)的约束，钢筋与混凝土之间不能采用嵌入(Embedded)的模式，可采用约束方程(Equation)建立热量传递的接触关系。有限模型中钢筋混凝土T形梁板的有限元网格划分及边界条件如图2所示，对流换热系数取25 W/(m2∙K)，辐射换热系数取0.5。

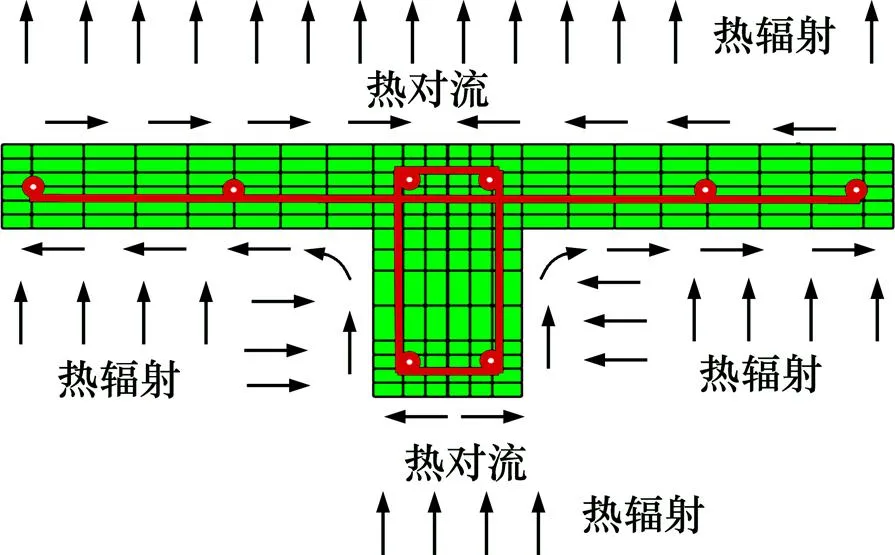
图2 钢筋混凝土T形梁模型

试件跨中截面的温度测点计算结果与试验结果对比如图3所示。可见：数值计算结果(实线)与试验实测结果(虚线)吻合较好，说明材料热工参数和有限元数值模型设置较合理。

(a) 试件CFRC-1；(b) 试件CFRC-2；(c) 试件CFRC-3；(d) 试件CFRC-4

文献[19]进行了钢筋混凝土矩形梁温度场的试验研究，试验升温曲线按照ISO-834标准升温曲线进行，试验梁截面长×宽为200 mm×200 mm，试验时钢筋混凝土矩形梁为三面受火，梁顶面为背火面。图4所示为截面中心线上到底面的距离为处的6个温度测点的实测数据和利用上述模型参数对试验进行的有限元计算结果。可见：有限元计算结果与试验实测结果基本吻合。

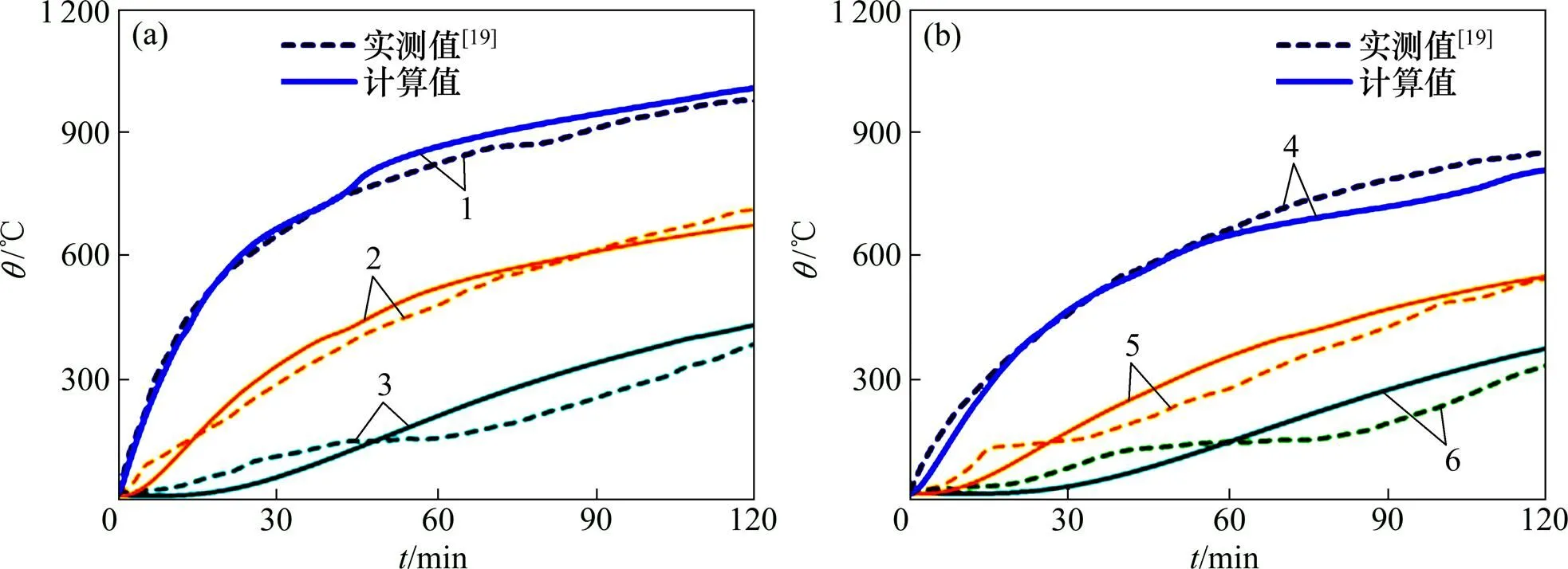
(a) d=0，20，70 mm；(b) d=10，40，100 mm

文献[20]进行了不同配筋率和保护层厚度的钢筋混凝土简支板恒载下的耐火性能试验研究。试验时，在构件中间沿截面高度设置镍铬−镍硅热电偶丝测量温度，选取构件B-2的试验数据(距板底受火面不同距离()的实测曲线)和有限元计算结果进行对比，如图5所示。从图5可见：钢筋混凝土板的有限元计算结果与实测结果吻合较好。

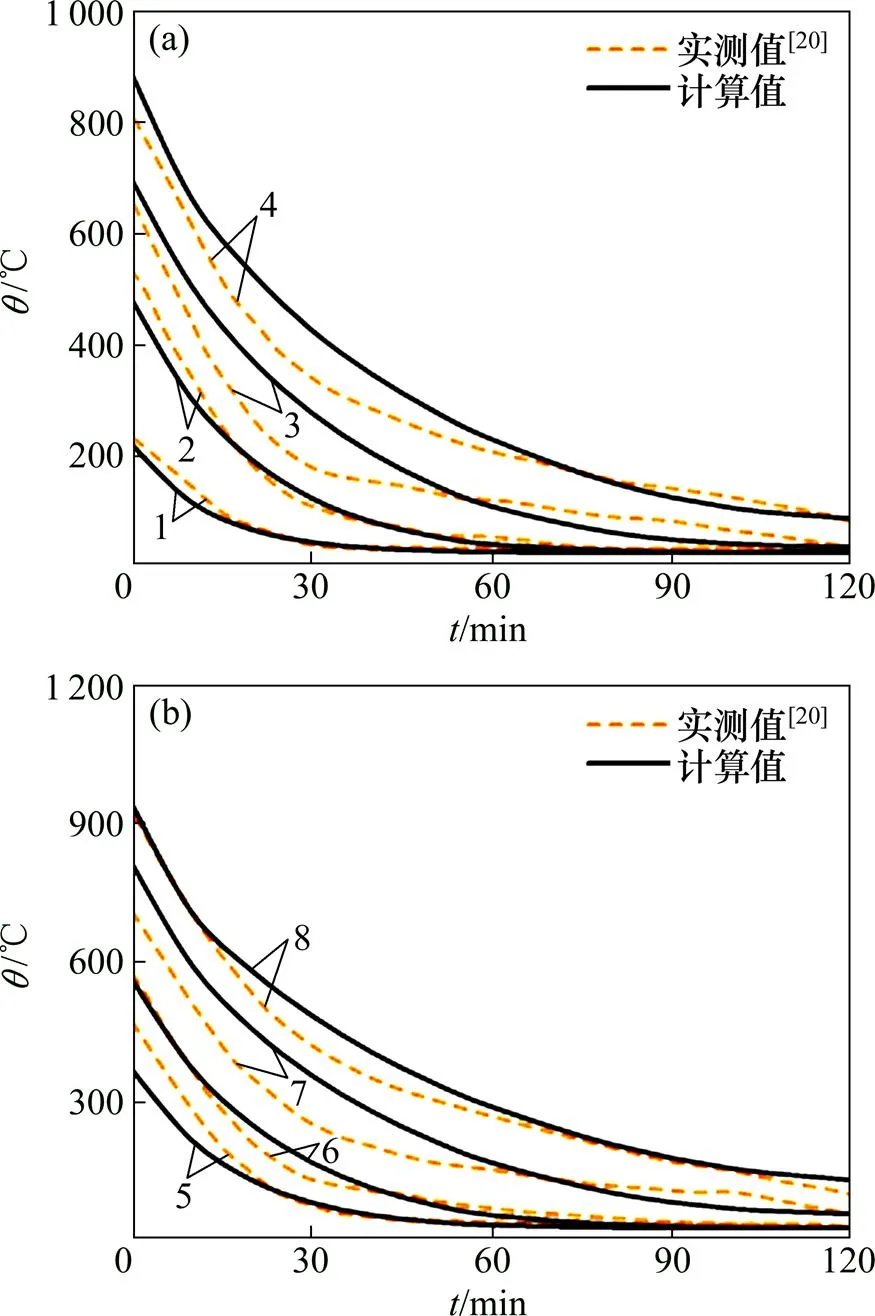
(a) d=5，15，35，70 mm；(b) d=10，20，50，90 mm

4 考虑升温和降温全过程温度场分析

基于ABAQUS有限元软件建立带楼板钢筋混凝土T形梁的温度场数值分析模型，试件参数如表2所示，截面尺寸和配筋见图6。混凝土强度C40(钙质骨料)，钢筋混凝土梁的混凝土保护层厚度为20 mm，楼板的混凝土保护层厚度为15 mm。升温曲线按照ISO-834标准升温曲线进行升温，T形梁板下部空间受火，楼板顶面为背火面。

表2 有限元分析模型参数

图6 截面尺寸和配筋(单位：mm)

图7所示为T形梁(RC-3)截面不同位置处测点的升温曲线，测点1~5分别位于楼板底(受火面)、楼板底层配筋处、楼板中线位置、楼板顶层配筋处和楼板顶面(背火面)位置。由图7(a)可见：由于T形梁腹板的吸热作用，使得腹板边缘处楼板厚度范围内的升温滞后于相邻的楼板，距离受火面越远，滞后时间越久。腹板所引起的升温滞后沿T形截面腹板向外逐渐减弱，腹板外侧约/2处的楼板截面测点升温曲线与楼板中部的升温曲线几乎重合，如图7(b)所示，说明距离T形腹板仅对相邻约/2范围内钢筋混凝土楼板的升温有影响。

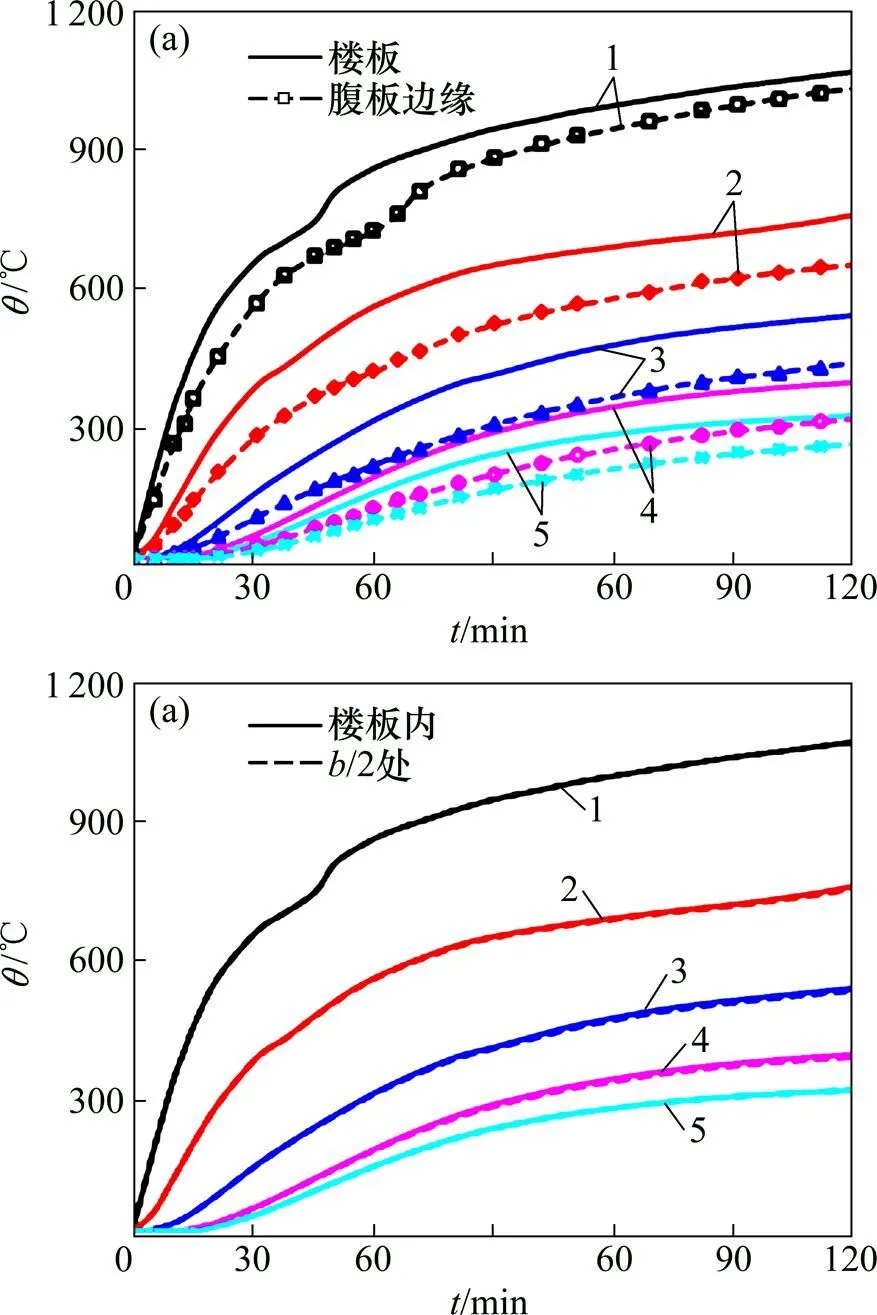
(a) 腹板边缘位置与楼板中部；(b) 腹板边b/2处与楼板中部

采用包含降温段的ISO-834标准升温曲线，对三面受火带楼板钢筋混凝土T形梁考虑升温和降温全过程的温度场进行分析。升温时间为180 min，此后按照ISO-834标准升温曲线中的降温段对带楼板钢筋混凝土T形梁的有限元模型进行传热计算，包含升温和降温全过程的总受火时间为440 min(此时ISO-834标准升温曲线降至常温26 ℃)。图8所示为不同降温时钢筋混凝土T形梁(RC-3)的截面温度场云图。从图8可见：当=180 min时，T形梁受火面空气的温度最高，此后受火面空气温度下降，热量开始由热空气向混凝土内部传递转变为混凝土高温区的热量同时向外(热空气)和向混凝土内部的低温区传递，即内部混凝土的温度变化存在滞后现象。距混凝土外表面的距离越大，时间滞后越久。在300 min时，混凝土截面的最高温度区位于受火面附近(深度为20~30 mm处)，约为763 ℃，而虽然此时T形梁矩形部分中心位置(测点2)的温度仅为600 ℃左右，但降温后该中心位置的温度仍略有升高，维持在600~620 ℃。其主要原因是中心位置下部高温区混凝土传递的热量在很长一段时间内与中心位置向上部混凝土低温区传递的热量相当，故该部分区域的混凝土未出现温度显著升高或降低的现象。当混凝土梁受火时间达到440 min时(结束时刻)，T形梁矩形部分中心位置及其下部的附近位置温度尚保持在600℃附近。与降温开始时刻(=180 min)中心位置的温度478 ℃相比，考虑升温和降温全过程后温度上升27%。

t/min：(a) 180；(b) 300；(c) 440

图9所示为钢筋混凝土T形梁截面测点1~6的全过程温度随受火时间变化情况，测点1~6布置如图9(f)所示。其中：测点1和测点4分别为钢筋混凝土梁中的下部和上部纵向钢筋处；测点2为T形梁腹板矩形部分(扣除翼缘厚度)的形心位置；测点3为T形梁腹板中线的上顶点，也是T形梁截面受火过程中的最低温度点；测点5为T形梁腹板侧面所对应的楼板下层钢筋配筋处；测点6为T形梁腹板侧面对应的楼板顶面位置。从图9可见：梁截面尺寸变化对测点2的升温曲线影响最大；随着梁截面尺寸增加，测点3和测点4的升温曲线略有降低(测点4温度的最大降低幅度约为150 ℃)；截面尺寸越大，混凝土内部达到最大温度所需的时间越久(升温滞后越严重)；当保持截面高宽比不变，梁高分别为=150，300和450 mm时，测点2达到最高温度的时间分别为268、382和440 min，其中梁高为450 mm的试件，至计算结束时刻，测点2的升温曲线尚处于上升段，但上升速率已十分平缓(曲线斜率接近于水平线)。保持梁宽不变仅增加T形梁的高度时，测点2的升温曲线变化规律与改变梁截面尺寸时相似，但变化幅度较小。当梁高分别为200，300和400 mm时，测点2达到最高温度的时刻分别为326，382和399 min，可见保持梁宽不变仅改变梁高对三面受火T形梁截面全过程的温度场分布和升温滞后的影响较小，说明实际曝火程度相近且宽度相同的楼面梁，在升温和降温全过程作用下的截面温度分布(受火程度)相近。

(a) RC-1；(b) RC-2；(c)RC-3；(d) RC-4；(e)RC-5；(f)温度测点布置

5 火灾后温度场分析

由于ABAQUS软件中的热传导模块可以记录每个节点温度变化的历史输出，但不能把每个节点的历史最高温度汇集起来，形成整个截面的火灾后历史最高温度分布。故在进行火灾后的力学性能分析时，有些研究忽略了火灾下温度场分布于火灾后历史最高温度分布的差异，直接采用火灾下某一时刻(如开始降温时刻)的温度场代替火灾后的历史最高温度。由上述分析可知，在升温段结束时(=180 min)，大部分混凝土截面的温度尚处于上升阶段，与升温结束时(=440 min)相比，T形梁矩形部分中心位置的温度尚能增加约30%。因此，在进行钢筋混凝土T形梁截面火灾后的力学性能分析时，不能仅依据升温或降温某一时刻的温度场分布来进行计算，否则分析结果可能使得估算的剩余承载力偏于不安全。

为了定量分析上述温度场的差异，采用用户自定义子程序对T形梁截面进行火灾后的历史温度分布研究。在每个计算增量步开始时刻，子程序自动提取上一个计算步的节点温度数据，并赋给1个自定义变量max，在该增量步结束时，将当前节点温度与自定义变量max进行对比，若当前节点温度大于max，则将当前节点温度赋予max，否则，继续进行下一增量步的计算，直至计算结束。最后得到的自定义变量max，即整个截面的火灾后历史最高温度。

图10所示为钢筋混凝土T形梁截面在升温或降温过程中某一时刻的温度场分布与火灾后的温度场分布(全截面为历史最高温度)对比。受火过程中热量由高温区向低温区域传递，T形梁截面中线上的温度梯度较大。在降温过程中，由于钢筋混凝土T形梁内部的热量继续传递，低温区混凝土截面温度继续升高，混凝土梁截面上的温度梯度进一步减小，使得混凝土过火面积(受温度显著影响的区域)进一步增加。依据500 ℃温度等值线所确定的带楼板钢筋混凝土T形梁过火面积将混凝土T形梁截面分为受火温度大于500 ℃的区域和受火温度小于500 ℃的区域。由图10(a)~(c)可见，由于钢筋混凝土板厚较小而受火面积大，历史最高温度的500 ℃温度等值线与升温或降温过程相比，距离受火面的深度由47 mm增加到51 mm；但在T形梁中线上的500 ℃温度等值线距离受火面(梁底面)的深度与升温或降温过程相比有大幅度增加，由升温结束时(=180 min)的105 mm增加到205 mm，混凝土截面过火温度超过500 ℃的面积有较大增加，如图10(c)所示。当截面尺寸较小时(=150 mm，=100 mm)，由于三面受火影响，T形梁腹板(矩形部分)的温度升高较快，受火后的500℃温度等值线与升温结束时(=180 min)相比差异不大，受火温度小于500℃的区域几乎与单面受火的钢筋混凝土楼板相同，如图10(d)和(e)所示。

(a) h=300 mm，b=200 mm，t=180 min；(b) h=300 mm，b=200 mm，t=200 min；(c) h=300 mm，b=200 mm，历史最高温度；(d) h=150 mm，b=100 mm，t=180 min；(e) h=150 mm，b=100 mm，历史最高温度

基于不同受火时刻或按照历史最高温度分布，分别以500 ℃温度等值线距离受火面的平均深度(如图9中虚线所示)来划分混凝土截面，以计算所得的大于500 ℃的混凝土截面面积(c1)与受火前混凝土总面积(c)的比值作为依据，初步估算钢筋混凝土T形截面火灾后的损伤情况，过火损伤系数di定义如下：

三面受火T形截面的过火损伤系数如表3所示。由表3可见，由于内部混凝土升温滞后作用，当升温曲线进入降温段(=200 mm)后， T形截面的过火损伤系数略有增加。与受火过程中的温度场相比，采用历史最高温度(max)的温度场所得到的过火损伤系数大于受火过程中的过火损伤系数，T形梁截面尺寸越大，火灾后(历史最高温度)与火灾下(升、降温过程中) 的损伤系数差异越大，最大差异可达17%。T形梁截面尺寸较小(=150 mm，=100 mm)时，火灾后与火灾下的过火损伤系数差别不大，主要原因是此时T形梁截面的温度场分布中温度小于500 ℃的区域与钢筋混凝土楼板单面受火时的分布相近，火灾后的过火损伤系数约为0.666。保持T形梁腹板宽度不变(=200 mm)仅改变梁高()，对过火损伤系数的影响不大，火灾后与火灾下的过火损伤系数变化幅度相近。

表3 三面受火T形截面的过火损伤系数

6 结论

1) 建立带楼板钢筋混凝土T形梁的温度场有限元分析模型，对分析模型进行试验验证，计算结果与试验结果较吻合。

2) T形梁腹板宽度对邻近翼缘(楼板)的温度场分布有影响，影响范围约为/2的邻近区域。

3) 混凝土内部升温与受火面相比存在滞后现象，且距离受火面的深度越大，升温滞后越明显。考虑升温和降温全过程的最高温度尚可上升约30%。

4) 火灾后(历史最高温度)与火灾下的温度场分布相比，T形梁截面温度存在不同程度升高。若采用火灾下(升温和降温过程)的温度场分布进行火灾后钢筋混凝土试件的力学性能分析，评估结果可能不安全。

[1] 时旭东, 过镇海. 钢筋混凝土结构的温度场[J]. 工程力学, 1996, 13(1): 35−43.
SHI Xudong, GUO Zhenhai. Analysis of the temperature field of reinforced concrete structure[J]. Engineering Mechanics, 1996, 13(1): 35−43.

[2] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998: 1−3.
YANG Shiming, TAO Wenshuan. Heat transfer theory[M]. Beijing: Higher Educational Press, 1998: 1−3.

[3] 金贤玉, 钱在兹, 金南国. 混凝土受火时温度分布的试验研究[J]. 浙江大学学报(自然科学版), 1996, 30(3): 286−294.
JIN Xianyu, QIAN Zaizi, JIN Nanguo. The study of temperature field in concrete members at elevated temperature [J]. Journal of Zhejiang University (Natural Science), 1996, 30(3): 286−294.

[4] Becker, R. Structural Behavior of simple steel structures with non-uniform longitudinal temperature distributions under fire condition[J]. Fire Safety Journal, 2002, 37(5): 495−515.

[5] 余志武, 王中强, 蒋丽忠. 火灾下钢筋混凝土板的温度场分析[J]. 铁道科学与工程学报, 2004, 1(1): 58−61.
YU Zhiwu, WANG Zhongqiang, JIANG Lizhong. Analysis of temperature field in reinforced concrete slabs exposed to fire[J]. Journal of Railway Science and Engineering, 2004, 1(1): 58−61.

[6] HAN Linhai, WANG Weihua, YU Hongxia. Experimental behaviour of reinforced concrete (RC) beam to concrete-filled steel tubular (CFST) column frames subjected to ISO-834 standard fire[J]. Engineering Structures, 2010, 32(10): 3130−3144.

[7] 熊伟, 李耀庄, 严加宝. 火灾作用下钢筋混凝土梁温度场数值模拟及试验验证[J]. 中南大学学报(自然科学版), 2012, 43(7): 2838−2843.
XIONG Wei, LI Yaozhuang, YAN Jiabao. Numeral modeling and experimental verification on heat transfer of RC beams under elevated temperature[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2838−2843.

[8] 杨志年, 董毓利, 吕俊利, 等. 整体结构中钢筋混凝土双向板火灾试验研究[J]. 建筑结构学报, 2012, 33(9): 96−103.
YANG Zhinian, DONG Yuli, LÜ Junli, et al. Experimental study of two-way reinforced concrete slab subjected to fire in a whole structure[J]. Journal of Building Structures, 2012, 33(9): 96−103.

[9] Kodur V K R, Yu B L, Dwaikat M M S. A simplified approach for predicting temperature in reinforced concrete members exposed to standard fire[J]. Fire Safety Journal, 2013, 56: 39−51.

[10] Ozˇbolt J, Bošnjak J, Periškic´G, et al. 3D numerical analysis of reinforced concrete beams exposed to elevated temperature[J]. Engineering Structures, 2014, 58: 166−174.

[11] Karakoc M B. Effect of cooling regimes on compressive strength of concrete with lightweight aggregate exposed to high temperature[J]. Construction and Building Materials, 2013, 41: 21−25.

[12] 韩林海. 钢管混凝土结构—理论与实践[M]. 2版. 北京: 科学出版社, 2007: 525−534.
HAN Linhai. Concrete filled steel tube structures: theory and experience[M]. 2nd ed. Beijing: Science Press, 2007: 525−534.

[13] BS ENV 1991-1-2: 2002, Eurocode 1: Actions on structures-Part 1-2: General actions – Actions on structures exposed to fire[S].

[14] Drysdale D D. An introduction to fire dynamics[M]. 2nd ed. New York: John Wiley and Sons, 1999: 59−79.

[15] Tan K H, Nguyen T T. Experimental and numerical evaluation of composite floor systems under fire conditions[J]. Journal of Constructional Steel Research, 2015, 105: 86−96.

[16] Rodrigues J P C, Correia A J M, Pires T A C. Behaviour of composite columns made of totally encased steel sections in fire[J]. Journal of Constructional Steel Research, 2015, 105: 97−106.

[17] Bamonte P, Lo Monte F. Reinforced concrete columns exposed to standard fire: Comparison among different constitutive models for concrete at high temperature[J]. Fire Safety Journal, 2015, 71: 310−323.

[18] 李国强, 韩林海, 楼国彪, 等. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006: 55−84.
LI Guoqiang, HAN Linhai, LOU Guobiao, et al. Fire resistance design of steel structures and steel-concrete composite structures[M]. Beijing: China Architecture&Buildings Press, 2006: 55−84.

[19] Haksever A, Anderberg Y. Comparison between measured and computed structural response of some reinforced concrete columns in fire[J]. Fire Safety Journal, 1981/1982, 4(4): 293−297.

[20] 陈礼刚. 钢筋混凝土板受火性能的试验研究[D]. 西安: 西安建筑科技大学建筑与土木工程学院, 2003: 33−39.
CHEN Ligang. Experimental research on fire resistance behavior of reinforced concrete slabs[D]. Xi’an: Xi’an University of Architecture and Technology. College of Architecture and Civil Engineering, 2003: 33−39.

Temperature distribution of reinforced concrete T-shaped beam with slabs under (after) three-side fire exposure

WANG Weihua, DONG Yuli

(College of Civil Engineering, Huaqiao University, Xiamen 361021, China)

To study the temperature distribution of reinforced concrete (RC) T-shaped beams combined with RC slabs subject to ISO-834 standard fire, of which three-side surfaces were heated, finite element (FE) models of the RC T-shaped beam with slabs were built using the nonlinear software ABAQUS. Parametric analysis was carried out on both the temperature distribution of the T-shaped beams with different sectional sizes and height-to-width ratios and the temperature distribution of the T-shaped beams subjected to the ISO-834 standard fire including cooling phase or after fire. The results show that RC slabs have large influence on the temperature distribution of T-shaped beams. The width of T-shaped beams has effect on the temperature rising in adjacent RC slabs. The fire duration time of inside concrete reaching the maximum temperature delays with the distance from the heated surface. The temperature distribution of T-shaped beams is quite different from that under high temperature (including cooling phase), so in the study of the mechanical behavior of the RC T-shaped beam, the temperature distribution after fire (the highest history temperature) should be used.

reinforced concrete; T-shaped beam; slab; temperature distribution; finite element analysis

TU352.5，TU378

A

1672−7207(2015)02−0684−10

2014−03−13；

2014−06−06

国家自然科学基金资助项目(51178143, 51208217)；华侨大学中青年教师科研提升资助计划项目(ZQN-PY215)；华侨大学科研基金资助项目(11BS417)(Projects (51208217, 51178143) supported by the National Natural Science Foundation of China; Project (ZQN-PY215) supported by the Promotion Program for Young and Middle-aged Teacher in Science and Technology Research of Huaqiao University; Project (11BS417) supported by the Science and Research Foundation of Huaqiao University)

王卫华，博士，讲师，从事钢与混凝土组合结构及抗火性能研究；E-mail：whwang@hqu.edu.cn

10.11817/j.issn.1672-7207.2015.02.042

(编辑 赵俊)