基于料层最高温度控制的铁矿烧结燃料合理分布

李法社，张小辉，张家元，田万一



基于料层最高温度控制的铁矿烧结燃料合理分布

李法社1，张小辉1，张家元2，田万一2

(1. 昆明理工大学 冶金与能源工程学院，云南 昆明，650093；2. 中南大学 能源科学与工程学院，湖南 长沙，410083)

利用所建立的铁矿石烧结过程传热数学模型，对某钢铁企业烧结机的常规烧结过程进行模拟计算，得到不同深度的料层最高温度分布，并通过烟气温度计算值与测试值的对比验证模型的可靠性。通过对料层本身所含热量和可利用热量的计算并结合料层最高温度合理取值，得到以0.04 m厚度为单元的各料层燃料含量合理取值，并以此为基础提出燃料合理分布的优化方案。与常规方案、基于平均分层的标准方案在料层最高温度稳定性、最高温度所在区域、冷却速度以及燃料含量的对比结果验证了优化方案的合理性和节能性。

铁矿烧结；数值模拟；配碳量；合理分布

铁矿石烧结常规工艺对铁矿粉等原料采取混合均匀后统一铺料的方式，降低了工艺过程和设备的复杂性，但会造成烧结料层的最高温度在料层深度方向上不稳定，即上部偏低，下部偏高，降低了设备的利用系数和成品烧结矿的产量和质量[1−2]，这种温度的不稳定性主要由料层的蓄热效应引起[3]。为在工程应用中解决这一问题，一些学者对烧结料层自动蓄热及燃料分层分布进行了研究，如：白晨光等[4]对料层厚度高度为0.3 m烧结料层的自动蓄热进行分析并以平均分层为基础，建立了蓄热模型，得到了各层的蓄热量比；黄柱成等[5]对高度为0.6 m烧结料层进行烧结热平衡分析和计算，提出了料层蓄热以及燃料合理分布的计算模型，并将整个料层平均分为3层进行燃料分层布料的烧结杯试验，得到了在不降低烧结矿质量的条件下，料层上、中、下3层的最优配碳量。这些研究考虑了技术应用的可行性，均是将整个料层平均分为3层，分别进行配碳量计算。自动蓄热量也是计算每层的总量和平均值，并没有结合常规工艺条件下料层最高温度的变化情况进行分层分析。吴胜利等[6]针对厚料层烧结中由自动蓄热引起的烧结过程的恶化，提出了改变燃料种类、燃料分加、燃料溶剂共同分加等方案，并通过试验证明了方案的有效性。这可以解决由于料层蓄热引起的燃烧带宽度增加导致的不利影响，但整个料层燃料均匀分布，料层最高温度依然会出现上低下高的现象。基于铁矿烧结过程的传热模型，本文作者对某钢铁企业烧结机的常规烧结工艺进行仿真计算，根据仿真得到的料层最高温度变化对料层深度单元进行合理划分，并以料层最高温度的合理值为目标计算每一单元的理论配碳量，以提高烧结矿产量、质量为目的，对烧结燃料的合理分布进行研究。

1 模型的建立

1.1 动量方程的修正

将烧结料层视为均匀多孔介质[7]，在此条件下，动量方程需要增加1个源项描述气体流动过程中的黏性和惯性损失[8]，该源项为

其中：和为给定矩阵；mag为速度绝对值。对于多孔介质内气流速度与压降的关系利用Ergun方程[9]计算：

其中：v为速度，m/s；为密度，kg/m3；为动力黏性系数，N∙s/m2；p为铁矿粉颗粒粒径，m；为料层孔隙率；y为气流速度，m/s。

1.2 双能量方程模型

对于料层内的气、固传热过程，利用基于局部非热力学平衡的双能量方程模型[9]对气相和固相分别建立能量方程。

固相：

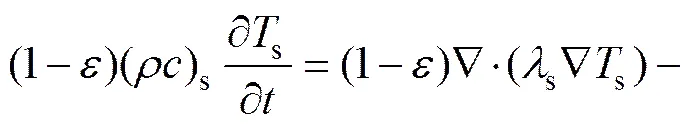
气相：

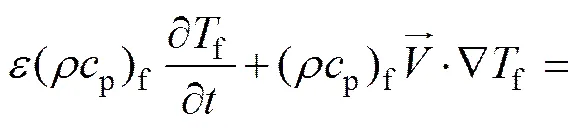
其中：s和f分别为固相和流体相的温度，K；v为体传热系数[8]，W/(m3∙K)；为内热源所产生的单位体积的热量，J；r为各反应所产生的反应热源项，J。

烧结过程产生热量变化的物理、化学反应主要是水分蒸发和冷凝、碳燃烧、碳酸盐分解、液相形成与凝固。对于水分蒸发，利用2个阶段模型[10−12]求解。

第1阶段，恒速蒸发，反应热源项[10]为

第2阶段，减速蒸发，反应热源项[10]为

其中：b为料层比表面积；w为H2O(g)传质系数；Δ1为水的汽化潜热，J；sat为颗粒表面饱和蒸气压；为水蒸气分压，Pa；和c为料层中含水量和临界含水量；w为H2O相对分子质量。对于冷凝，反应热源项[12]为

对于燃料燃烧，反应热源项[13]为

其中：c为燃料颗粒粒径，m；为综合反应速率常数；为氧气体积分数；c为单位体积内碳颗粒数；Δc为碳的低位热值，J/kg。对于碳酸盐分解，反应热源项[10]为

其中：l为石灰石颗粒比表面积，1/m；l为分解开始温度，K；l为分解度相关系数，为传热系数，W/m2∙K。对于液相的形成与凝固[14−15]，反应热源项分别为：

其中：mlt为开始熔化(凝固)温度；Δmlt熔化(凝固)过程反应热。

1.3 计算区域离散

在烧结机台车中心选取长×宽×高为0.40 m×0.40 m×0.63 m的区域建立物理模型，从料面到0.60 m深度处为烧结原料层，底部0.03 m为铺底料层。该计算区域内的烧结过程与台车内实际烧结过程一致，该模型的4个侧面具有对称性特点。使用结构性网格对该区域进行离散化，网格最小尺寸为0.01 m，网格总数为10.08万。图1所示为计算区域的网格示意图。

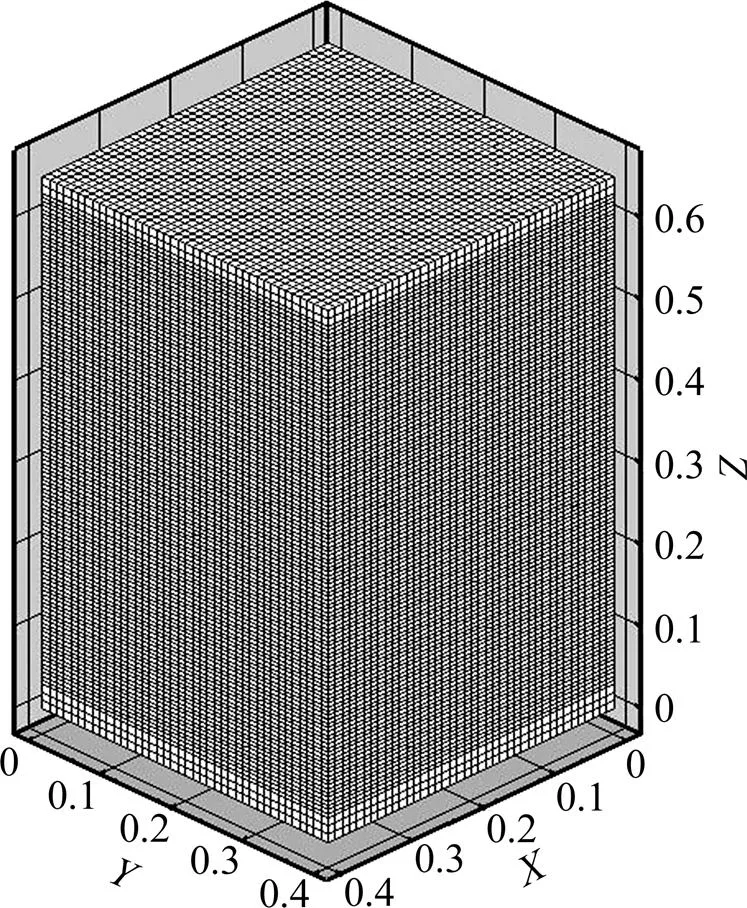
图1 计算区域网格示意图

1.4 计算方法和边界条件

利用−湍流模型，对压力−速度耦合采用SIMPLE算法，对湍动能、湍流耗散率的离散采用二阶迎风格式。对能量方程的非稳态项、源项采用FLUENT的UDF功能编写程序定义。计算区域进气口定义为速度入口，速度根据实际流量计算得到。烟气出口定义为压力出口，点火阶段为−10 kPa，常温抽风烧结阶段为−15 kPa，侧面为对称边界。

2 常规烧结工艺计算结果及分析

2.1 模型验证

本文所采用的烧结原料的组成、配比及含水率均来自于某钢铁企业烧结生产技术中心，如表1所示。其中，燃料由焦粉和无烟煤组成，其工业分析结果如表2所示。

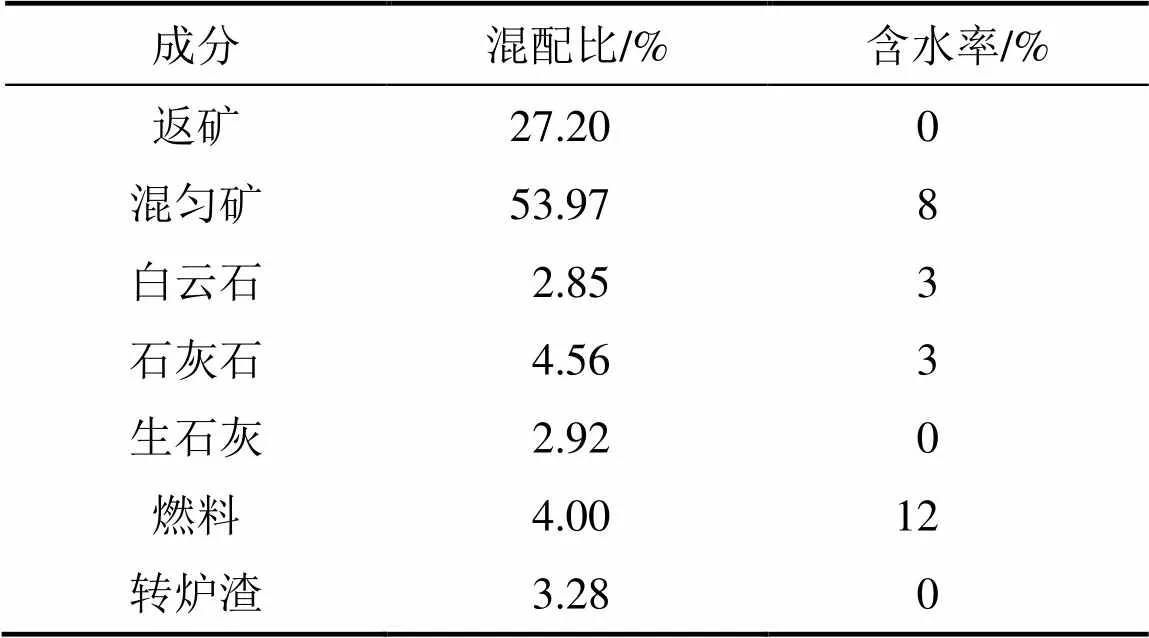
表1 烧结矿原料组成、配比及含水率

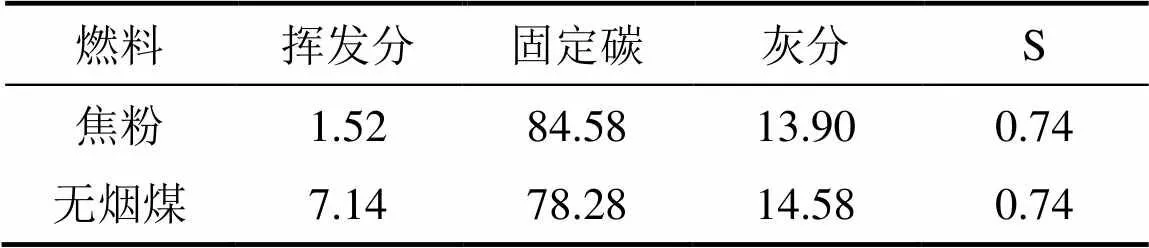
表2 燃料的工业成分分析(质量分数)

为验证计算模型的可靠性，并考虑到料层内温度测试的可操作性，结合烧结机台车的现场条件，以台车出口处风箱内烟气温度的测试值对计算结果进行验证。测点设置在1，3，5，…，23号风箱弯管处，进行多次测量并取平均值。烟气温度计算值与测试值对比如表3所示。

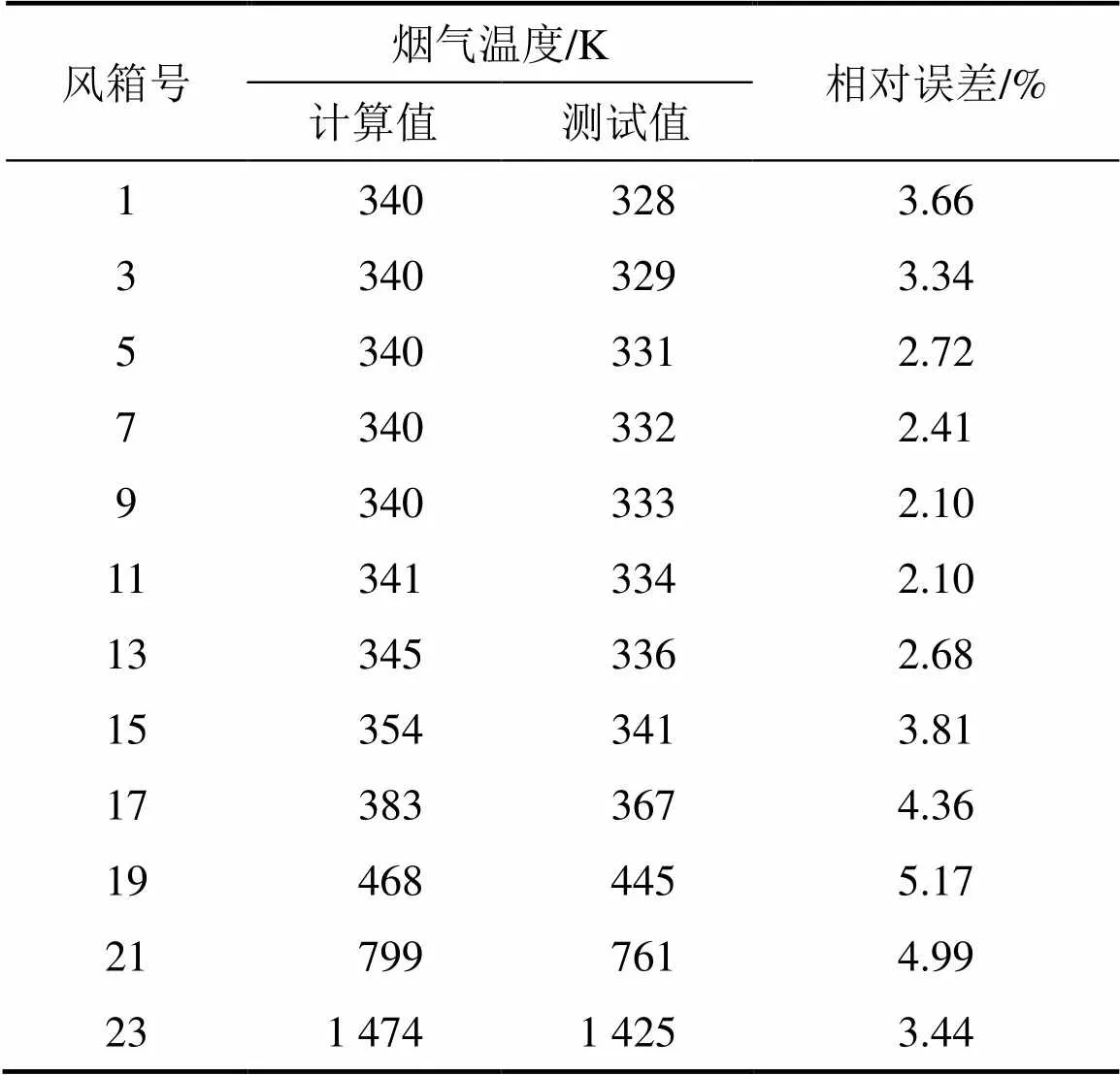
表3 计算值与测试值对比

烟气温度的计算值相对于测试值均偏大，主要原因有2个：一是烧结设备存在一定的漏风率；二是烧结台车、风箱壁面等与周围空气存在热交换。由表3可知：烟气温度计算值与测试值的变化趋势一致，最大相对误差小于6.00%，因此，可认为计算模型是正确和可靠的。

2.2 结果分析

判断烧结料层中燃料分布是否合理的依据是不同深度料层的最高温度分布，根据料层温度的分布以及料层本身热量和可利用热量计算合理燃料的温度分布。图2所示为基于常规烧结工艺计算得到的不同深度料层最高温度分布情况。

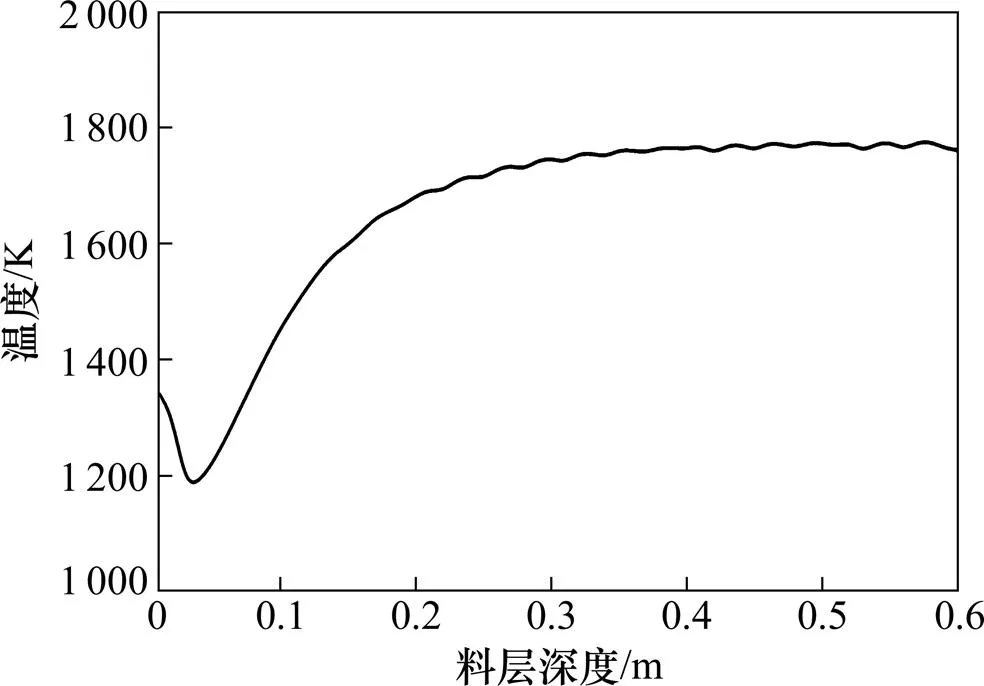
图2 不同深度料层最高温度的变化

由图2可知：从料面到0.2 m深度处的料层最高温度变化较大，这主要是因为：1) 从高温点火到常温抽风烧结，进入料层的气体温度在较短时间内由点火温度(1 473 K)降低到常温，引起料层最高温度不断降低(从料面到深度0.04 m处)；2) 在常温抽风烧结稳定之后，燃料的燃烧使得料层开始蓄热，因此，料层温度又开始上升(从深度为0.04 m到0.20 m)。在深度0.20 m以下的料层，最高温度较稳定。这是因为料层自身所含燃料的燃烧放热以及上部料层带入的可利用蓄热量，使得料层达到熔融状态，由于这一相变的吸热量较大，料层的热量主要用于相变过程[15−16]，对料层的温度影响较小。

3 燃料合理分布研究

造成料层温度在深度方向上不稳定的原因，除了在烧结过程中进入料层气体物性参数的变化所引起外，另一个重要的原因就是料层的自动蓄热作用[4]。烧结过程参数的变化由烧结工艺决定，而自动蓄热作用则可以通过燃料合理分布来降低其对料层温度波动的影响。料层的蓄热量是指由空气从上单元料层带入本单元料层的热量。在实际计算中，某单元料层的蓄热量为达到该单元料层最高温度时所需的热量与料层本身所含热量之差。对于单元料层的厚度的确定，考虑到计算的准确性和降低计算过程的复杂性，取为0.04 m，将整个料层分为15个计算单元，分别定义为单元1、单元2等。对每一单元理论燃料含量的计算过程和步骤如下：

1) 确定单元最高温度的合理取值，即确定温度目标。一般烧结过程料层合适的最高温度为1 573~1 723 K[17]。本文以这一范围的中间值为目标值，即1 648 K。

2) 计算达到目标值时料层需要的热量1。在该计算过程中，假定料层的质量不变，并对料层的比热容进行分段线性化处理。

3) 根据单元燃料量、溶剂量、含水量等主要引起热量变化的参数，计算单元本身所含热量2。对于单元1，需要考虑由点火、保温带入该单元的热量。

4) 根据本单元实际温度，计算达到该温度时所需要的热量3。计算方法与计算1的计算方法相同。

因此，本单元的蓄热量为

对于料层上部单元，会出现3＜2的情况。这是因为进入料层的气体温度在短时间内急剧降低加快了热交换，使得料层由于烧结反应放出的热量小于由气流带走的热量，此时该单元的蓄热量计为0。该烧结厂混合原料中燃料质量分数(4%)作为基准来计算各单元的理论配碳量，其计算式为

据此得到的各单元理论配碳量如表4所示。

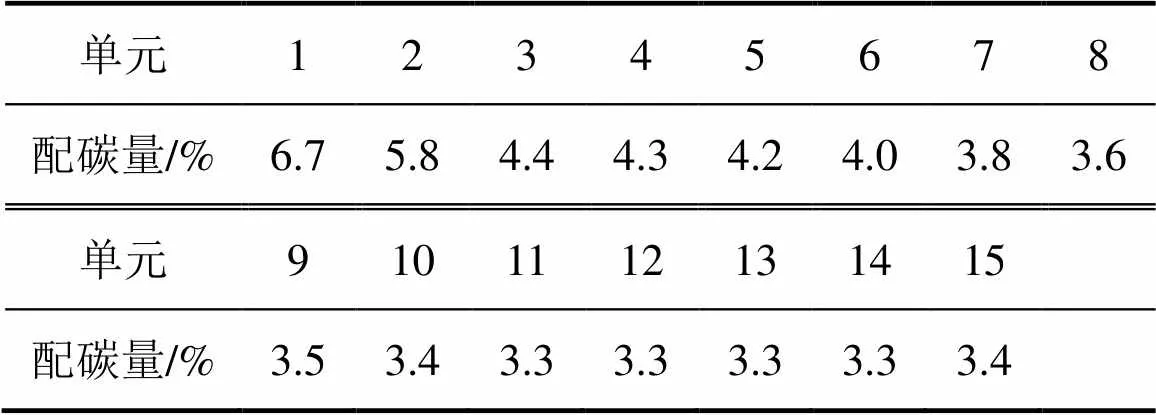
表4 各单元配碳量计算值

由表4可知：单元1和2的配碳量较大，其差值也较大。这是由于该单元蓄热量较低且入口气体温度由点火(1 473 K)、保温(873 K)到常温(303 K)不断降低，对这2个单元的影响较大。在单元3以后，随着深度的增加，一方面烧结趋于稳定，另一方面蓄热量也逐渐增加，所需要的燃料量呈稳定降低的趋势。

表4中各单元的配碳量为理论计算值，若按此配比来添加燃料则大大降低了铺料的可行性。根据烧结过程燃料合理分层的研究[4−5]，宜将料层分为3层来添加燃料。这3层的厚度以及配碳量的确定方法如下：根据单元间配碳量变化幅度的特点，将单元1和2定为第1层，单元3至9为第2层，单元10至15为第3层；第1层含碳量取2个高度区域的平均值6.3%，然后利用式(6)计算第2和第3层的含碳量，结果分别为3.6%和3.3%。经计算得到厚度为0.6 m烧结料层的合理燃料分布及分层情况如表5所示。

表5 燃料合理分布方案

4 结果分析与对比

以原料中燃料含量4%为基准，根据对料层可利用蓄热率[4]的计算方法，得到平均分层条件下，上、中、下层燃料配比分别为4.9%，3.9%和3.2%，将这一燃料配比方案称为标准方案，将前面得到的燃料合理分布方案称为优化方案。以下将对标准方案和优化方案分别进行计算，并将其结果与常规方案所得结果进行对比分析。

4.1 温度对比

烧结过程的顺利进行以及成品烧结矿质量的提高受烧结过程中料层温度的影响，料层的温度是各种烧结反应和原料熔融结晶的推动力[18]。对于不同烧结工艺，对比其料层温度的变化具有重要意义。图3所示为上述3种燃料分布方案在不同深度处最高温度的变化情况。

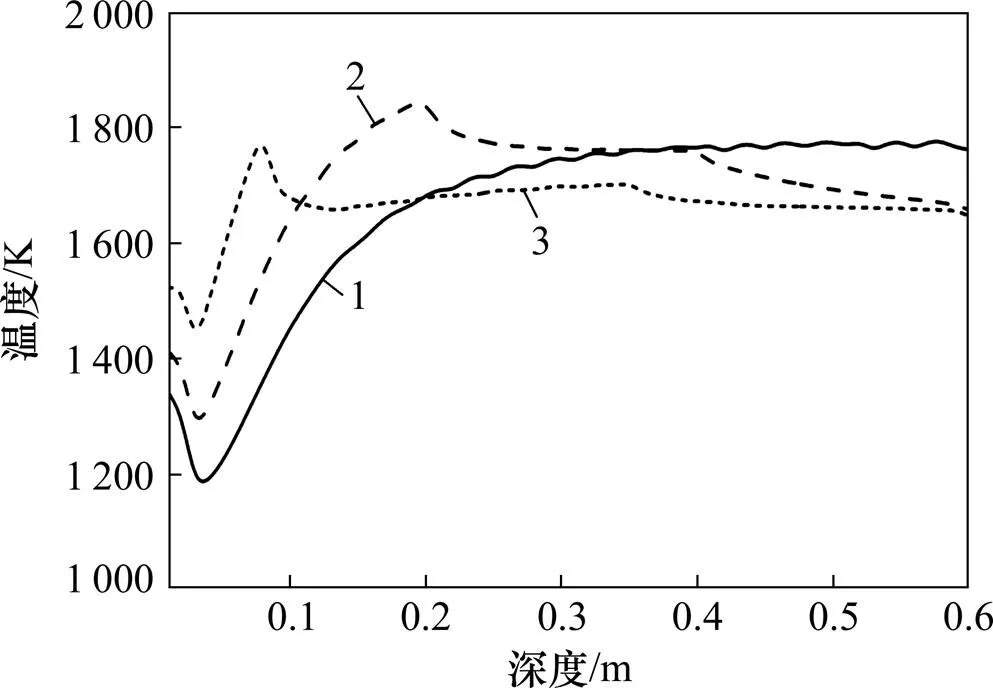
1—常规方案；2—标准方案；3—优化方案

由图3可知这3种方案的最高温度在不同深度有不同的特点：在0~0.1 m深度内，优化方案平均温度最高，为1 610 K，常规方案最高温度的极差最小；0.1~0.4 m深度内标准方案平均温度最高，为1 771 K，优化方案最高温度的极差最小；0.4~0.6 m深度内常规方案平均温度最高，为1 768 K，优化方案最高温度的极差最小。通过以上分析和对比可知：在点火、保温到常温空气抽风烧结的初始阶段，由于操作参数改变导致上部料层温度过低以及由于蓄热作用导致料层下部温度过高的现象，可以通过合理分配燃料来改进；同时，燃料的合理分布也扩大了料层最高温度稳定区域的厚度，可以提高成品矿的产量和质量。

图4~6所示分别为3种方案在不同时刻的中心纵截面料层温度分布云图。

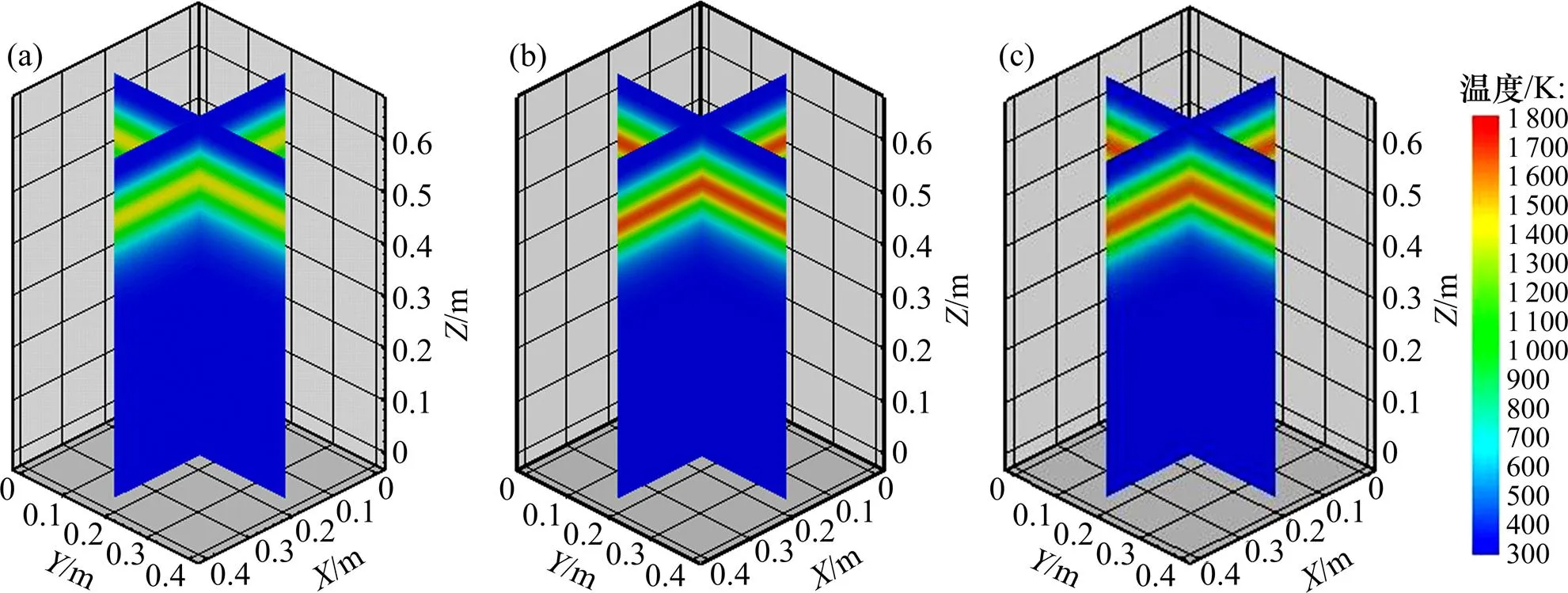
(a) 常规方案；(b) 标准方案；(c) 优化方案

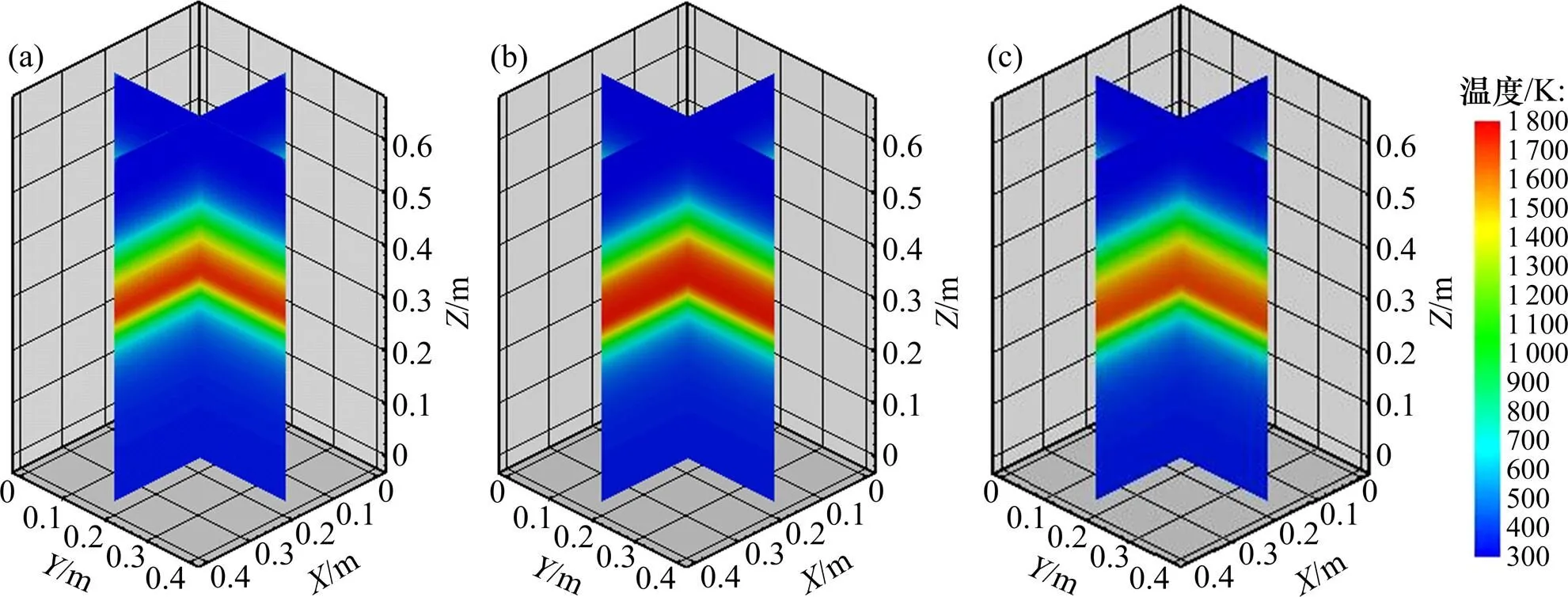
(a) 常规方案；(b) 标准方案；(c) 优化方案

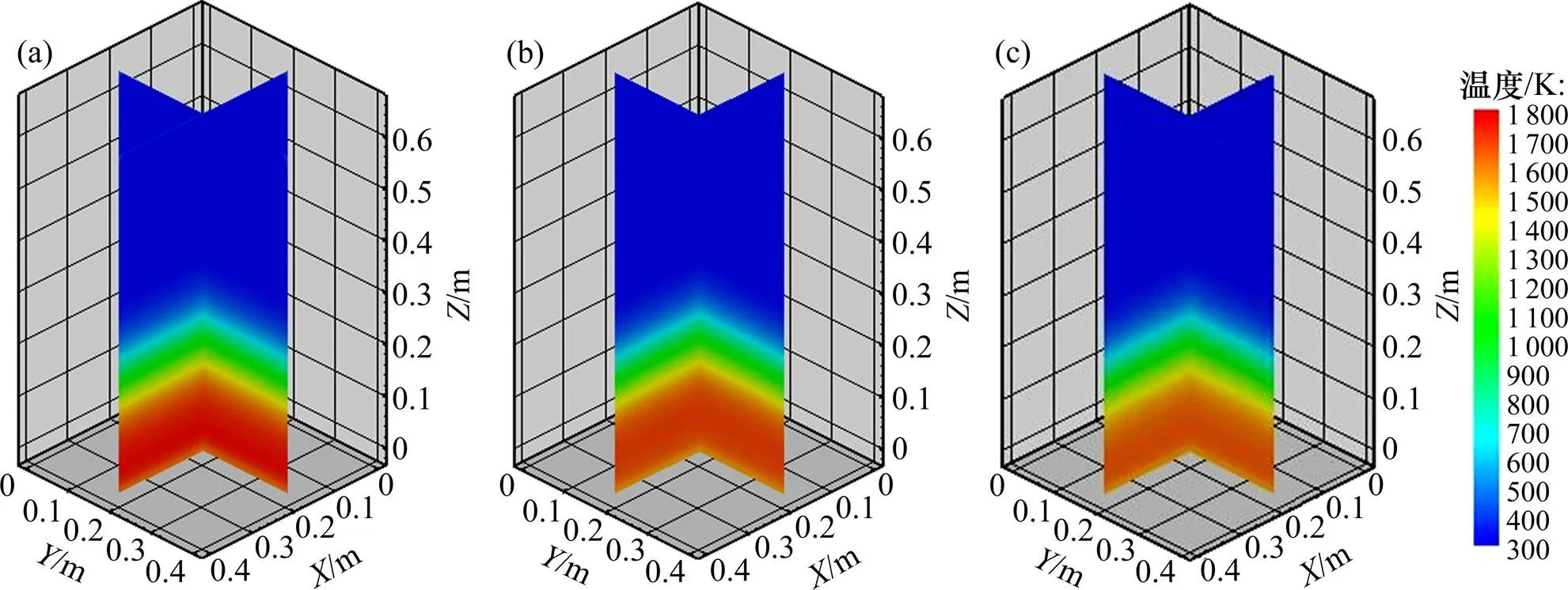
(a) 常规方案；(b) 标准方案；(c) 优化方案

从图4~6可以看出：在500 s时，标准方案、优化方案提高了料层的最高温度，优化方案增加了高温区的厚度；在1 000 s时，标准方案的料层温度最高，标准方案和优化方案均提高了高温区的厚度，且烧结前沿较常规方案的低，说明标准方案和优化方案的烧结进度比常规方案的快；在卸料点时，常规方案的料层温度最高，这3种方案的高温区厚度较一致。通过比图4~6可知：合理调整料层燃料分布情况，可使料层的最高温度在深度方向上趋于稳定，因而使得烧结过程也更加稳定。

4.2 燃烧带厚度对比

燃烧带厚度的变化会影响烧结矿质量。燃烧带厚度过大，会影响料层的透气性，不利于烧结过程的顺利进行；燃烧带厚度过小，会导致燃烧带热量少，温度低，产生的液相量不足，烧结矿黏结不好，强度低。以上3种方案在不同时刻的燃烧带厚度对比结果如表6所示。

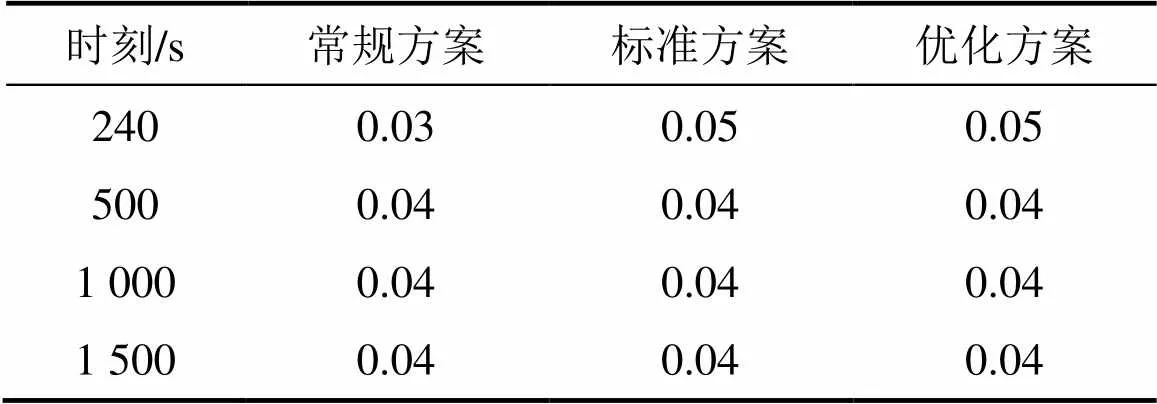
表6 燃烧带厚度

表6中的240 s为保温阶段结束时刻。由表6可知：标准方案与优化方案在240 s时的燃烧带厚度相对于常规方案均增加了0.02 m。这是因为标准方案与优化方案均增加了上部料层的配碳量，增强了燃料的燃烧强度，提高了上部料层的最高温度，因此，标准方案和优化方案能促进上部料层烧结矿质量提高。从整个料层在不同时刻燃烧带厚度的变化也可看出标准方案和优化方案的料层燃烧稳定性更好。

4.3 基于料层温度的烧结矿质量对比

烧结过程中料层的温度及变化特点影响烧结矿的质量[19]，其中主要决定因素为料层最高温度的范围及冷却速度。本文以这2个指标对上述3个方案进行对比，以评价其成品矿质量。

1) 料层最高温度。按料层最高温度是否在合理温度范围内将料层分为3个区间，即低于下限、高于上限和位于合理范围内。以上3方案料层最高温度所在的区间厚度见表7。

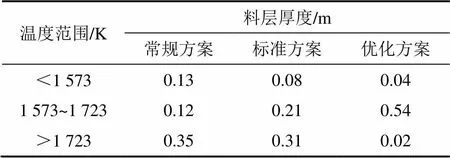
表7 料层最高温度区间及厚度

位于合理温度范围内的料层厚度越大，说明烧结反应进行越顺利，原料的熔化和结晶效果更好。由表7可知：优化方案的料层最高温度分布最合理，说明燃料分布最合理；常规方案位于合理温度区间内的料层厚度最小，造成上部缺少热量、下部热量过剩，中间合理热量区域较少的热量分布不合理的现象；标准方案中超过合理温度区间上限的料层厚度也较大，应适当降低这些料层中燃料含量。

2) 冷却速度。烧结料层中的燃料反应完全之后便进入冷却过程。冷却速度是指料层从最高温度降低到料层开始凝固时(mlt)的降温速率，对于到达卸料点时温度仍高于凝固温度的料层，取达到最高温度之后180 s内的降温速率作为冷却速度。由于原料及配比不同，合理的料层冷却速度也不同，在一般情况下，其值以不超过120 K/min为宜[17]。3种方案在不同深度的料层冷却速度如图7所示。

1—常规方案；2—标准方案；3—优化方案

3种方案的冷却速度位于合理范围内的料层厚度如下：常规方案为0.408 m，标准方案为0.411 m，优化方案为0.462 m。冷却速度超过合理范围，说明料层冷却速度过大，会使烧结过程中产生的热应力残留在烧结矿中，从而形成较多的裂纹，降低了成品矿的强度，增加了脆性。因此，冷却速度位于合理范围内的料层厚度越大，所形成的成品矿质量越好。可见优化方案的成品矿质量最优。

4.4 燃料使用量的对比

根据前面得出的优化方案燃料分布及相应的料层厚度，计算各自的总燃料使用量，并与常规方案、标准方案进行对比，结果表明常规方案、标准方案和优化方案的配碳量分别为4.00%，4.00%和3.84%。可见：优化方案相对于常规方案和标准方案，燃料量节约4.00%，这对于能量消耗基数较大的烧结工艺来说，节能效果明显。

5 结论

1) 建立了铁矿石烧结过程的传热计算模型，并对某钢铁企业烧结机的常规工艺进行了数值计算，通过计算值与测试值的对比验证了模型的可靠性；以料层最高温度为优化指标，提出了铁矿烧结的燃料合理分布优化方案。

2) 优化方案和标准方案的最高温度位于合理取值范围的料层厚度较常规方案分别提高了350%和75%；优化方案和标准方案的冷却速度位于合理范围的料层厚度较常规方案分别提高了13.2%和0.7%。说明通过对燃料的调整分配，改善了料层最高温度的分布，使得不同深度料层的最高温度趋于稳定，提高了料层烧结过程的稳定性。

3) 优化方案的燃料使用量较常规方案和标准方案降低了4%，说明燃料合理分配对铁矿烧结过程具有良好的节能效果。

[1] 唐先觉, 何国强. 论我国30年来铁矿烧结的技术进步[J]. 烧结球团, 2009, 34(6): 8−11.
TANG Xianjue, HE Guoqiang. On technological progress of iron ore sintering over the past 30 years in China[J]. Sintering and Pelletizing, 2009, 34(6): 8−11.

[2] 郜学. 中国烧结行业的发展现状和趋势分析[J]. 钢铁, 2008, 43(1): 88−91.
GAO Xue. Development situation and trend analysis of sintering industry in China[J]. Iron and Steel, 2008, 43(1): 88−91.

[3] 冯根生, 吴胜利, 赵佐军. 改善厚料层烧结热态透气性的研究[J]. 烧结球团, 2011, 36(1): 5−9.
FENG Gensheng, WU Shengli, ZHAO Zuojun. Research on improving hot permeability of deep bed sintering[J].Sintering and Pelletizing, 2011, 36(1): 5−9.

[4] 白晨光, 谢皓, 邱贵宝, 等. 烧结料层中的蓄热模型[J]. 重庆大学学报(自然科学版), 2008, 31(9): 1002−1007.
BAI Chenguang, XIE Hao, QIU Guobao, et al. An accumulation heat model and its application in iron ore sintering[J]. Journal of Chongqing University (Natural Science Edition), 2008, 31(9): 1002−1007.

[5] 黄柱成, 江源, 毛晓明, 等. 铁矿烧结中燃料合理分布研究[J]. 中南大学学报(自然科学版), 2006, 37(5): 884−890.
HUANG Zhucheng, JIANG Yuan, MAO Xiaoming, et al. Fuel appropriate distribution in iron ore sintering[J]. Journal of Central South University (Science and Technology), 2006, 37(5): 884−890.

[6] 吴胜利, 陈东峰, 赵成显, 等. 提高厚料层烧结燃料燃烧性的试验研究[J]. 钢铁, 2010, 45(11): 16−21.
WU Shengli, CHEN Dongfeng, ZHAO Chengxian, et al. Study on improving combustion of solid fuel in deep bed sintering[J]. Iron and Steel, 2010, 45(11): 16−21.

[7] 张小辉, 张家元, 戴传德, 等. 烧结矿冷却过程数值仿真与优化[J]. 化工学报, 2011, 62(11): 3081−3087.
ZHANG Xiaohui, ZHANG Jiayuan, DAI Chuande, et al. Optimization and simulation of sinter cooling process[J]. CIESC Journal, 2011, 62(11): 3081−3087.

[8] 刘伟, 范爱武, 黄晓明. 多孔介质传热传质理论与应用[M]. 北京: 科学出版社, 2006: 32−36.
LIU Wei, FAN Aiwu, HUANG Xiaoming. Porous media theory and application of heat and mass transfer[M]. Beijing: Science Press, 2006: 32−36.

[9] Ergun S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48(2): 89−94.

[10] Lovel R, Vining K R, Amico M D. The influence of fuel reactivity on iron ore sintering[J]. ISIJ International, 2009, 49(2): 195−202。

[11] Komarov S V, Shibata H, Hayashi N, et al. Numerical and experimental investigation on heat propagation through composite sinter bed with non-uniform voidage: Mathematical model and its experimental verification[J]. Journal of Iron and Steel Research International, 2010, 17(10): 1−7.

[12] Lü X W, Bai C G, Qiu G B, et al. Kinetics of water absorption by the bed of iron ore particles during granulation[J]. Powder Technology, 2010, 204(1): 138−144.

[13] Sadrnezhaad S K, Ferdowsi A, Payab H. Mathematical model for a straight grate iron ore pellet induration process of industrial scale[J]. Computation Materials Science, 2008, 44(2): 296−302.

[14] Yang W, Choi S, Choi E S, et al. Mathematical model of thermal processes in an iron ore sintering bed[J]. Metals and Materials International, 2004, 10(5): 493−500.

[15] Tan P, Neuschütz D. Study on polychlorinated dibenzo-p- dioxin/furan formation in iron ore sintering process[J]. Metallurgical and Materials TransactionsB, 2004, 35(5): 983−991.

[16] 张小辉, 张家元, 张建智, 等. 铁矿石烧结过程传热传质数值模拟[J]. 中南大学学报(自然科学版), 2013, 44(2): 805−810.
ZHANG Xiaohui, ZHANG Jiayuan, ZHANG Jianzhi, et al. Numerical simulation of heat and mass transfer in sintering process[J]. Journal of Central South University (Science and Technology), 2013, 44(2): 805−810.

[17] 龙红明. 铁矿粉烧结原理与工艺[M]. 北京: 冶金工业出版社, 2010: 97−123.
LONG Hongming. Principles and technology of iron ore sintering[M]. Beijing: Metallurgical Industry Press, 2010: 97−123.

[18] 董辉, 林贺勇, 张浩浩, 等. 烧结热工测试与分析[J]. 钢铁, 2011, 46(11): 93−98.
DONG Hui, LIN Heyong, ZHANG Haohao, et al. Thermal test and analysis of sintering cooling system[J]. Iron and Steel, 2011, 46(11): 93−98.

[19] 刘斌, 冯妍卉, 姜泽毅, 等. 烧结床层的热质分析[J]. 化工学报, 2012, 63(5): 1344−1353.
LIU Bin, FENG Yanhui, JIANG Zeyi, et al. Heat and mass transfer in sintering process[J]. CIESC Journal, 2012, 63(5): 1344−1353.

Fuel appropriate distribution based on the highest temperature control in iron ore sintering

LI Fashe1, ZHANG Xiaohui1, ZHANG Jiayuan2, TIAN Wanyi2

(1. Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming 650093, China;2. School of Energy Science and Engineering, Central South University, Changsha 410083, China)

A mathematical model of heat transfer in iron ore sintering was established. The highest solid temperature in different depths was obtained to simulate conventional sintering of sinter trolley in an iron and steel company, and the reliability of this model was verified by comparing the simulated and tested values of the flue gas temperature. The reasonable fuel content in every unit thickness(0.04 m) of sintered bed was obtained based on heat calculations and the reasonable highest solid temperature. The optimization solution of fuel appropriate distribution was proposed, and it is proved to be reasonable and energy saving by contrast with conventional and standard solution in respect of the stability and range of the solid highest temperature, the cooling rate and the fuel content in sintered bed.

iron ore sintering; numerical simulation; fuel content; appropriate distribution

TF 046.4

A

1672−7207(2015)02−0386−08

2014−06−20；

2014−08−15

云南省人才培养项目(KKSY201452018)；教育部博士点基金资助项目(KKQX201352004) (Project (KKSY201452018) supported by Talent Cultivation of Yunnan Province; Project (KKQX201352004) supported by PhD Programs Foundation of Ministry of Education of China)

张小辉，博士，讲师，从事冶金过程节能减排研究；E-mail: xiaohui6064@sina.com

10.11817/j.issn.1672-7207.2015.02.002

(编辑 陈灿华)