地铁区间隧道顶部热烟气温度分布

刘方，翁庙成，余龙星，李罡，廖曙江



地铁区间隧道顶部热烟气温度分布

刘方1, 2, 3，翁庙成1, 2, 3，余龙星1，李罡1，廖曙江4

(1. 重庆大学 城市建设与环境工程学院，重庆，400045；2. 重庆大学 三峡库区生态环境教育部重点实验室，重庆，400045；3. 重庆大学 低碳绿色建筑国际联合研究中心，重庆，400045；4. 重庆市公安消防总队，重庆，401121)

通过调查统计重庆地铁6号线区间隧道的断面形式，引入隧道断面形状系数，建立断面形状系数＜1的模型实验台。采用模型实验与FDS模拟相结合的方法，探讨地铁隧道采用纵向排烟系统时，不同热释放速率及排烟速度的条件下区间隧道内烟气温度纵向分布特征。研究结果表明：Kurioka模型适用于断面形状系数≥1的地铁区间隧道，对于断面形状系数＜1的地铁区间隧道，需要对Kurioka模型进行修正。对于断面形状系数≥1的地铁区间隧道，顶棚上游烟气温度纵向分布服从指数衰减规律。然而，对于断面形状系数＜1的地铁区间隧道，顶棚上游烟气温度虽然也服从指数衰减规律，但需要进行模型修正。修正值与断面形状系数之间满足线性关系，顶棚上游烟气温度沿纵向衰减速度，随隧道断面形状系数的增大而增大。

安全工程；区间隧道火灾；烟气温度；相似模型实验；计算机模拟

由于结构的特殊性，隧道一旦发生火灾，不仅严重威胁人的生命及财产安全、对隧道运营设备造成巨大的损失及不良的社会影响，而且会对隧道的建筑结构造成严重的破坏。发生火灾时，燃烧释放的高温烟气将主要聚集在隧道顶部，当隧道顶部的温度升高到一定值之后，顶部混凝土将发生爆裂，使得隧道顶板中的钢筋裸露出来。而钢筋在超过一定的温度后，其强度会大大下降，这将可能导致隧道的坍塌[1−5]。因此，大多数隧道中都采用防火板和喷涂防火涂料对隧道的内部结构进行防火保护。国内外的研究者对隧道火灾时拱顶附近的最高烟气温度以及隧道火灾烟气纵向温度分布规律进行了大量的实验测试与数值模拟研 究[6−8]。隧道最高烟气温度模型以及烟气纵向温度分布规律的研究对于指导隧道结构防火设计具有重要意义。研究表明，隧道火灾烟气温度受到很多因素的影响，如火灾规模、通风风速以及隧道几何尺寸等。Kurioka等[9]在5个不同尺寸的隧道上开展了隧道火灾近火源区域温度预测的实验研究，得出了隧道拱顶最高温度预测模型。国内学者彭伟等[10−13]通过实体实验和模型实验验证了Kurioka 模型的可靠性。近年来，还有研究者开展了坡度对隧道拱顶最高温度的影响研究，提出了坡度修正的Kurioka 模型[14−16]。Hu等[17−19]通过理论分析、大尺寸模拟实验和全尺寸现场实验相结合的方法，研究了隧道火灾烟气的流动特性，建立了隧道火灾烟气温度纵向分布规律的预测模型，证实了隧道火灾烟气温度沿隧道纵向变化呈指数衰减的规律。上述隧道顶部最高烟气温度以及隧道火灾烟气温度纵向分布规律的预测模型的研究主要针对公路隧道进行的，而公路隧道的主要特点是断面大，除特殊地段外，基本上多数是双车道和三车道，而铁路和地铁车站及区间隧道其断面形式往往要小于公路隧道，多数是单道单行线，断面形式也别于公路隧道。因此，这就意味着公路隧道拱顶附近烟气最高温度的预测模型以及隧道火灾烟气温度纵向分布规律的预测模型是否可以用于指导地铁区间隧道的设计值得进一步探讨。本文作者对重庆6号线区间隧道断面形式进行了调查分析，利用FDS模拟研究9种不同隧道横截面形式在不同纵向通风风速下火灾时隧道顶部最高烟气温度，根据模拟数据对Kurioka 模型进行修正。通过相似模型实验台以及实体实验结果对修正的Kurioka 最高温度模型进行验证。同时，通过FDS模拟、相似模型实验台以及实体实验结果进一步证实火灾烟气温度纵向分布呈幂指数衰减的规律，以便为区间隧道火灾的工程实践提供参考。

1 区间隧道断面形式

隧道高度是影响隧道烟气运动的重要参数之一，当隧道横截面面积相同，高的隧道内的烟气卷吸冷空气量比隧道高度低的少，但隧道高度不宜独立作为影响烟气运动的参数。隧道的横截面面积和隧道高度同时影响烟气运动。因此，综合考虑隧道高度和横截面对烟气运动的影响，引入隧道形状系数作为技术参数，隧道形状系数为

式中：为隧道横截面面积，m2；为隧道高度，m；为隧道形状系数。

对重庆市轨道交通六号线区间隧道的断面形式进行调查，统计6号线58个隧道的断面形式，其隧道高度为4.300~11.037 m，隧道面积在19.38~134.95 m2；单洞单向隧道断面形状系数为0.63~0.97，单洞双向隧道断面形状系数为1.01~1.85，区间隧道长度为757~ 6 701 m。隧道主要断面形式为矩形、圆形和马蹄形。

2 数值模拟分析

2.1 模拟方案

根据调查结果，选取9种典型断面形式的隧道进行模拟计算，其断面形式如图1所示。其中，除隧道H和I为单洞双向隧道外，其余均为单洞单向隧道。此外，隧道A~F，宽度相同高度不同，而隧道D和G高度相同宽度不同。隧道C为马蹄形隧道，其余为矩形隧道，模拟方案如表1所示。

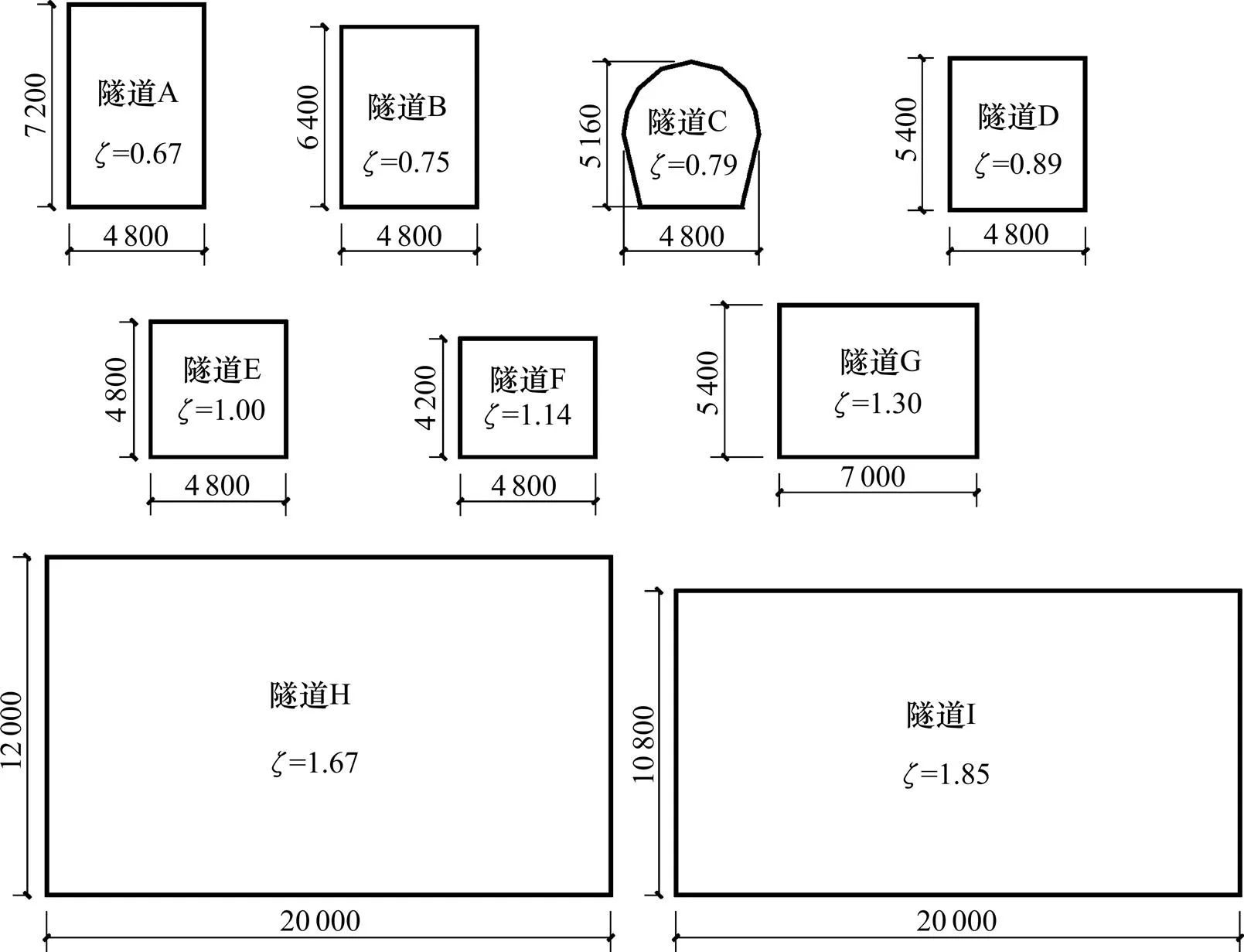
图1 隧道断面形式(单位：mm)

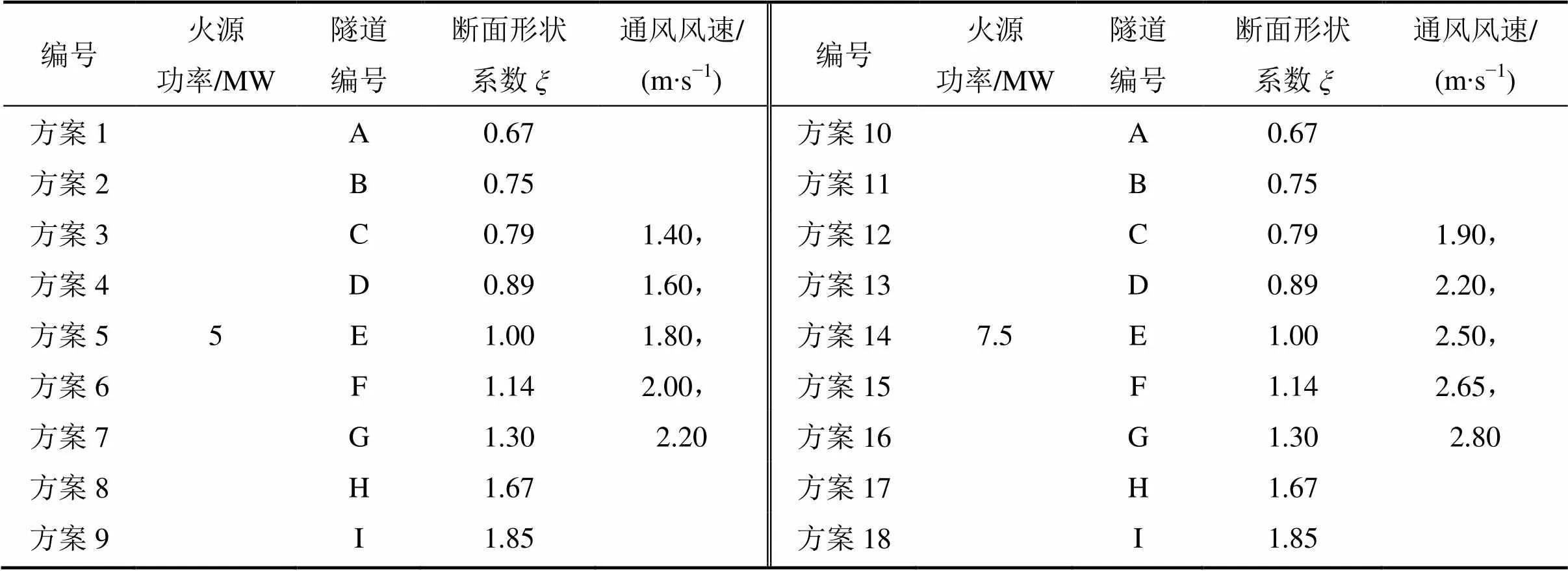
表1 FDS模拟方案

在FDS数值模拟中，根据国内外大量研究已经证实，网格尺寸=0.1*时，计算结果能够准确描述区间隧道内各参数的变化[20]，*为火源特征直径，m，计算公式如下：

式中：为重力加速度；T为发生火灾前隧道内空气温度，K；为火源热释放速率，kW；为环境空气密度，kg/m3；c为空气定压比热容，J/(kg∙K)。

2.2 最高温度及沿程温度分布模型

Kurioka模型为

=1.77，=6/5(当时)

=2.54，=0(当时)

式中：Δmax为最高烟气温升，K；*和分别为热释放速率和弗劳德数，和为系数；H为火源表面至隧道顶部高度，m；为纵向通风风速，m/s。

胡隆华模型如下式所示：

式中：为距火源的距离，m；0为参考点据火源的距离，m；T为距火源为m处的烟气温度，K；0为参考点温度，取隧道顶部烟气最高温度处为参考点，0=max；，和为常量，=1，=−/=−0.035。

2.3 模拟结果分析

2.3.1 最高温度预测模型

将模拟结果整理为最高温度与无因次量的关系，见图2。从图2可见：当断面形状系数≥1时，烟气最高烟气温升Δmax与Kurioka的预测模型中的基本一致，即对于断面形状系数≥1的隧道，烟气最高烟气温升Δmax可以采用Kurioka的预测模型预测。因为Kurioka 模型实验中的5个不同尺寸隧道的形状系数介于1~3之间，因此≥1的隧道，模拟结果与Kurioka的预测模型结果很吻合。而当断面形状系数＜1时，烟气最高烟气温升Δmax比 Kurioka预测模型的最高温度低，其最高温升的计算公式如下：

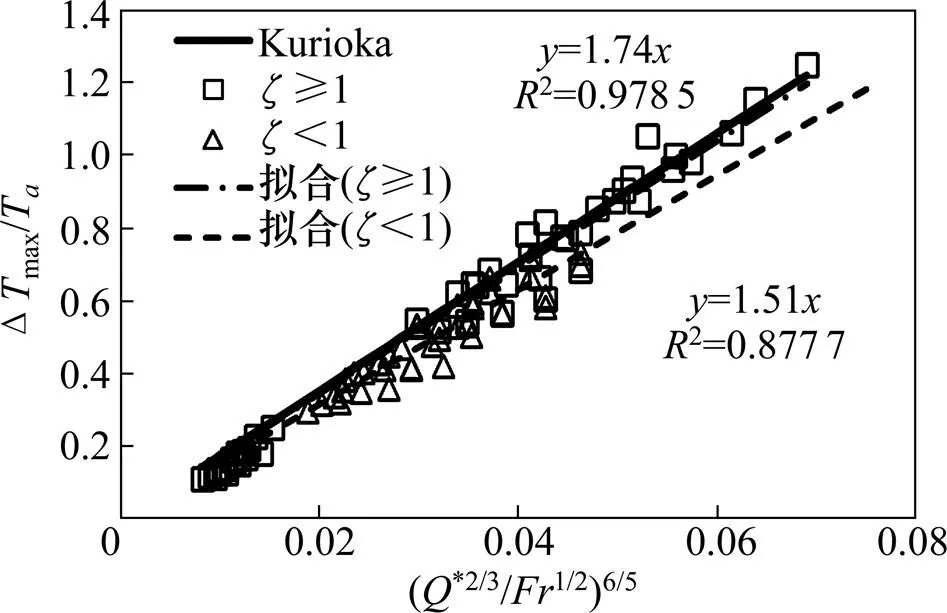
图2 最高温升模拟值与Kurioka模型预测值对比图

2.3.2 烟气纵向温度分布规律

将隧道顶棚上游温度纵向数值模拟结果整理为无量纲温升Δx/0与距参考点距离的关系，当火源功率为5 MW和7.5 MW时，断面形状系数小于1的隧道顶棚上游烟气温度纵向分布如图3所示。

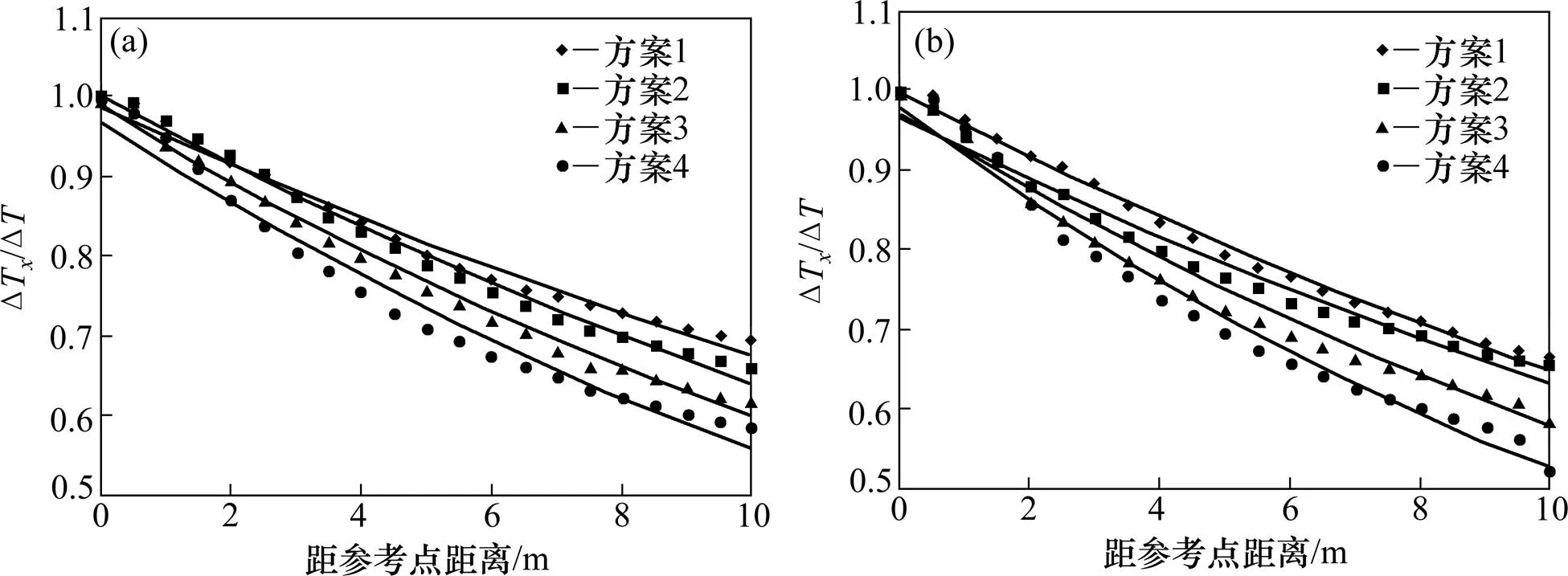
火源功率/MW：(a) 5.0；(b) 7.5

由图3可知：1) 对于断面形状系数小于1的隧道，顶棚上游烟气温度沿隧道纵向分布仍然符合胡隆华模型的指数衰减规律。2) 对于断面形状系数小于1的隧道，随着隧道断面形状系数的增大，隧道顶棚上游烟气温度沿隧道纵向衰减速率增加。这是因为隧道断面形状系数越小，其烟羽发展受到限制，烟气温度沿程衰减减慢。

由于隧道顶棚上游烟气温度沿隧道纵向衰减速率与隧道断面形状系数有关。因此，对隧道顶棚上游温度数值模拟结果进行指数衰减拟合，引入修正值对衰减速率进行修正，拟合结果以及衰减速率修正值如表2所示。修正后的隧道火灾烟气温度纵向分布预测模型为

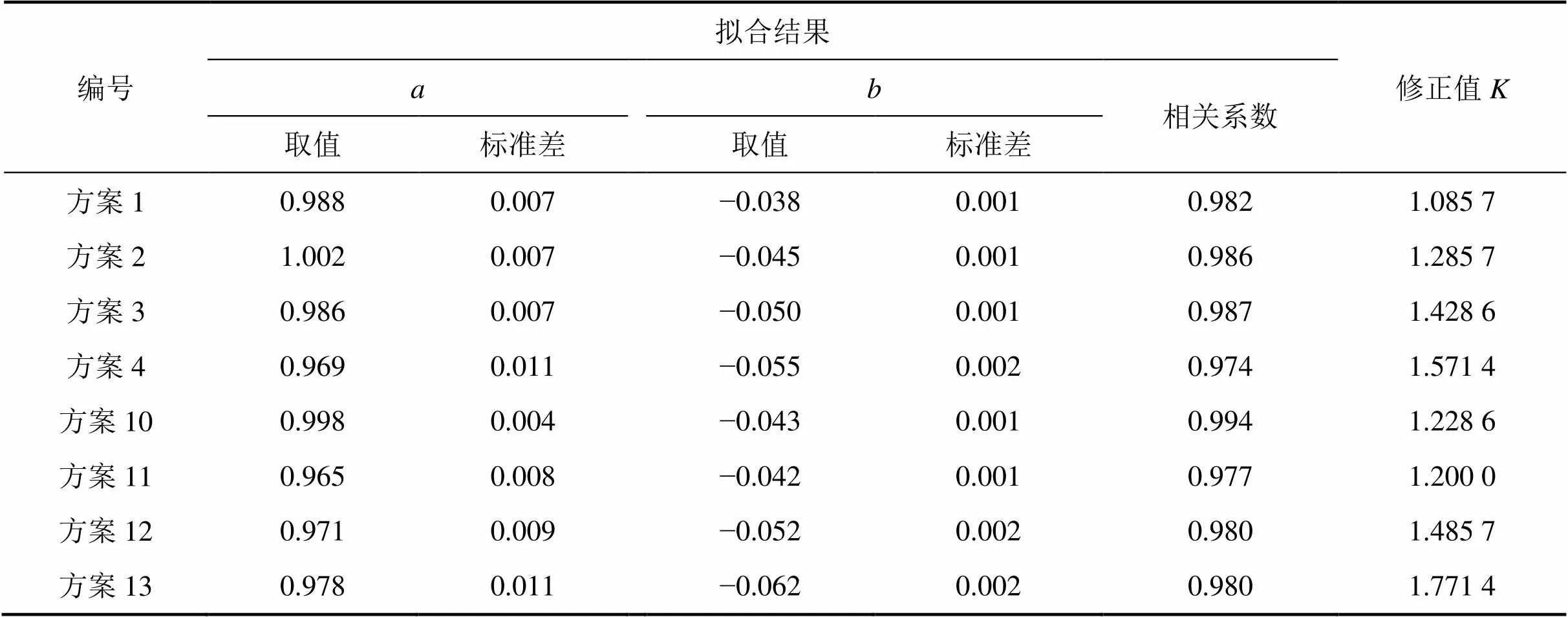
表2 隧道顶棚上游温度衰减数值模拟拟合结果

衰减速率与断面形状系数的关系如图4所示，在修正值中引入断面形状系数对衰减速率进行修正，可以得出线性修正结果为

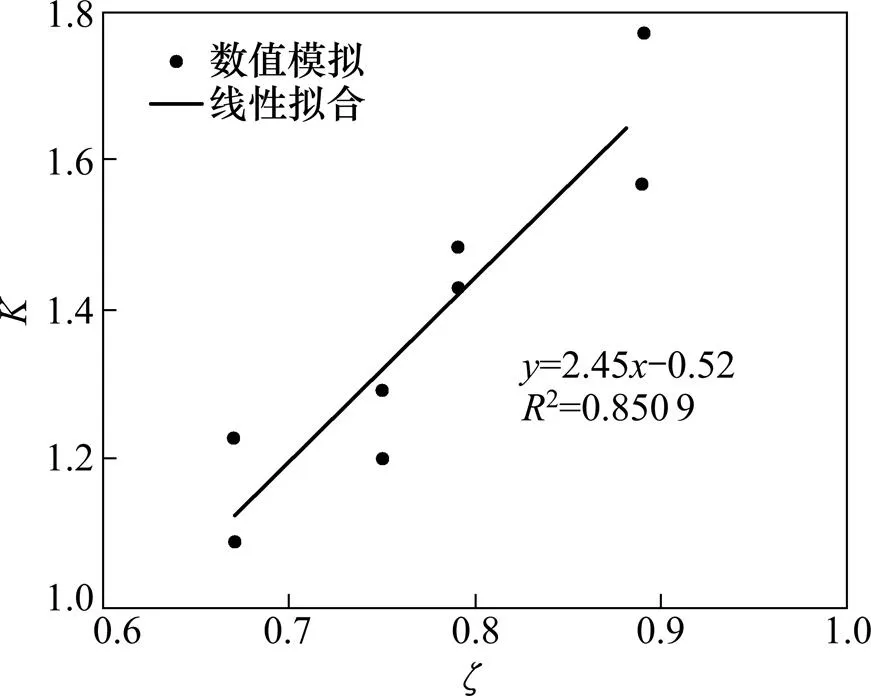
图4 衰减速率修正值与断面形状系数关系

即对于断面形状系数小于1的隧道，隧道内上游任意点的拱顶烟气温度可以结合式(8)和式(9)计算求得，顶棚上游烟气温度沿隧道纵向分布规律可以用下式表示：

3 相似模型实验及全尺寸实验

3.1 相似模型实验理论

本文采用弗诺德模型设计相似模型实验台，几何相似关系为

温度场相似关系为

m=f(12)

速度相似关系为

进风口和排烟体积流量相似关系为

火源强度相似关系为

其中：下标m代表模型，下标f代表原型。

3.2 相似模型实验装置

本文模型隧道采用1:10的几何比尺设计，隧道模型纵向断面长×宽为540 mm×480 mm(=0.89)，隧道纵向长度为15 m，由5段拼接而成，每段长度为3 m。两侧材料采用6 mm厚的防火玻璃，顶部烟道和底部材料采用8 mm厚的防火板。模型隧道安置在1 m高的底座上，底座采用型钢制作。

模型隧道的进口端安装有一台轴流式送风机，出口端则与外界相通。送风机的风量=1 000 m3/h，静压为150 Pa。采用变频调节器控制电动机转速，以得到所需的不同送风量。在模型隧道内每隔一定距离放置1把刻度标尺，实验时采用摄像机记录烟气层的高度变化。

实验中模拟火源采用工业甲醇，其纯度为95%。热释放速率通过记录燃料质量损失来计算。利用本课题组研发的分离式耐高温电子秤和数据采集系统，实时测量并记录甲醇质量随时间的变化，从而由甲醇质量变化曲线的斜率得到甲醇油盘的质量损失速率*。设计长×宽分别为8 cm×8 cm，10 cm×10 cm，12 cm×12 cm，15 cm×15 cm以及15 cm×20 cm的油盘，油盘深度为5 cm。油盘尺寸规格及其对应的热释放速率如表3所示。

表3 油盘尺寸规格及其对应的热释放速率

由于甲醇燃烧时发烟量较小，需要添加一定的示踪物体来产生烟气以便观察。本实验中示踪物采用成分为硫磺和锯沫的烟饼。同时，采用K型铠装热电偶测量火灾时隧道内空间各点温度，通过温度采集模块将接受到的温度信号传输至数据采集仪，并连接到计算机进行实时监测。隧道一侧安装送风风机，采用调速电机对风量进行调节，可在模型隧道中形成0~1 m/s 的纵向风速。数据采集系统对模型隧道内温度和流速进行测量。在隧道拱顶下方1 cm 沿纵向每隔20 cm 布置1个热电偶温度测点，每隔3 m布置1个风速测量截面(图5)，并布有8个测温截面和4个测速截面，具体各测点布置如图5 和图6 所示。

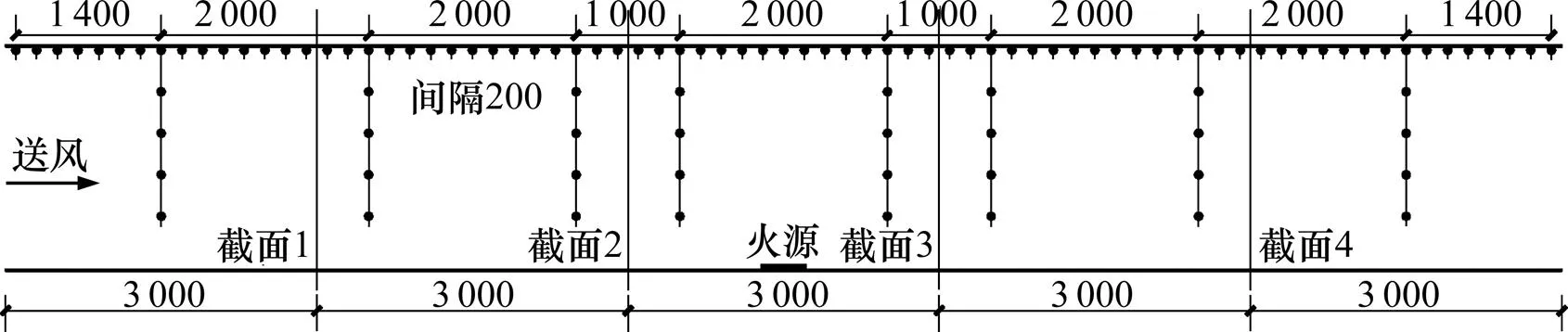
图5 隧道纵向测点布置示意图(单位：mm)

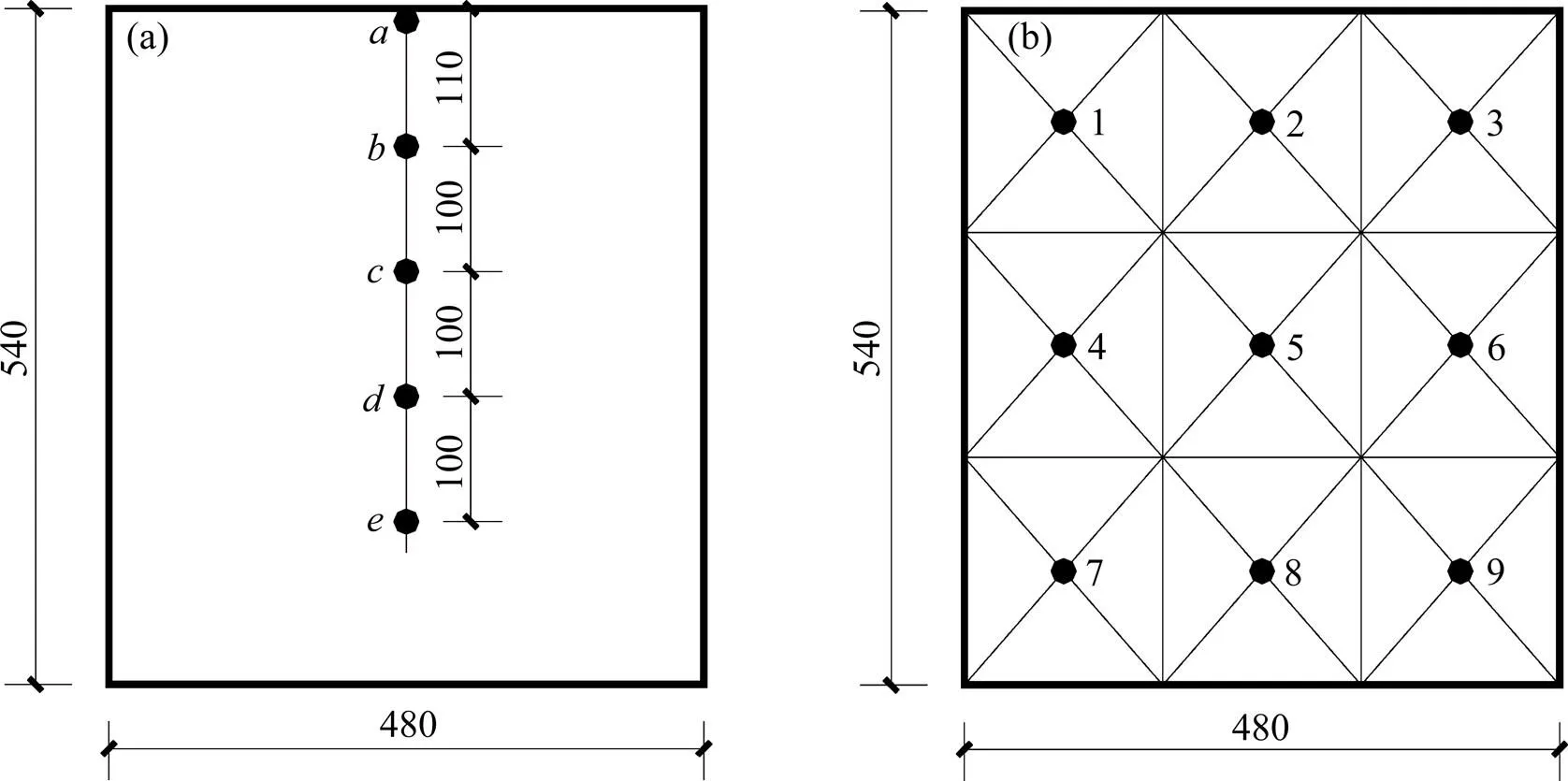
(a) 截面热电偶测点布置；(b) 截面风速测点布置

3.3 相似模型实验方案

本次实验共进行25组实验，火源功率分别为1.59，3.19，4.78，8.97和12.38 kW。表4所示为相似模型实验方案及其最高温度。

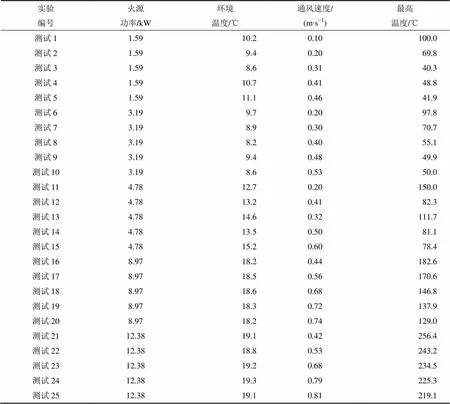
表4 相似模型实验方案及其最高温度

3.4 全尺寸实验

在重庆某一段349 m长的地铁区间隧道内开展全尺寸的火灾实验研究。火灾烟气实验在长度为211.2 m的单洞单向隧道内进行。该段隧道高度为5.16 m，下部宽度为4.8 m，其断面形状系数=0.79，隧道断面示意图如图7所示。

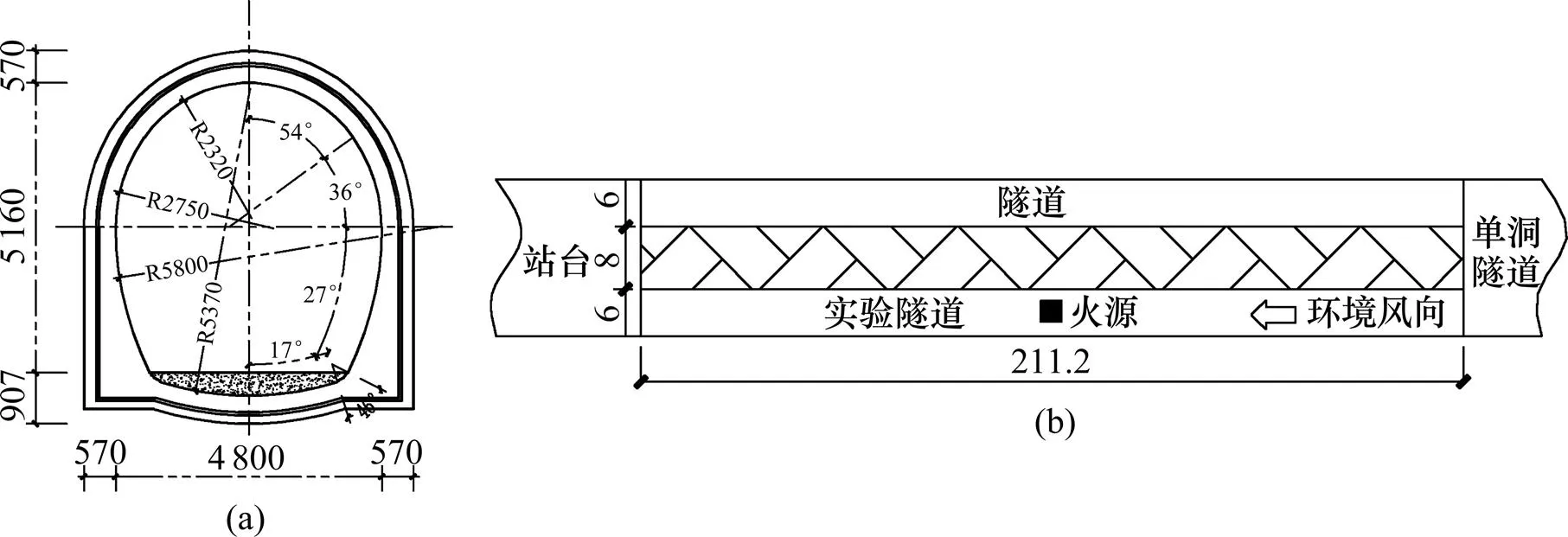
(a) 实验区间隧道段断面示意图(单位：mm)；(b) 实验区间隧道纵向示意图(单位：m)

采用不同尺寸规格的油盘进行3组实验，通过控制油池的面积和油量来控制火灾功率，火源功率分别为0.90，1.35和1.8 MW，测试时的环境温度以及风速如表5所示。实验采用K型铠装热电偶测量火灾时隧道内顶部各点烟气温度，通过温度采集模块将接受到的温度信号传输至数据采集仪，并连接到计算机进行实时监测，3次实验隧道顶棚最高温度见表5。

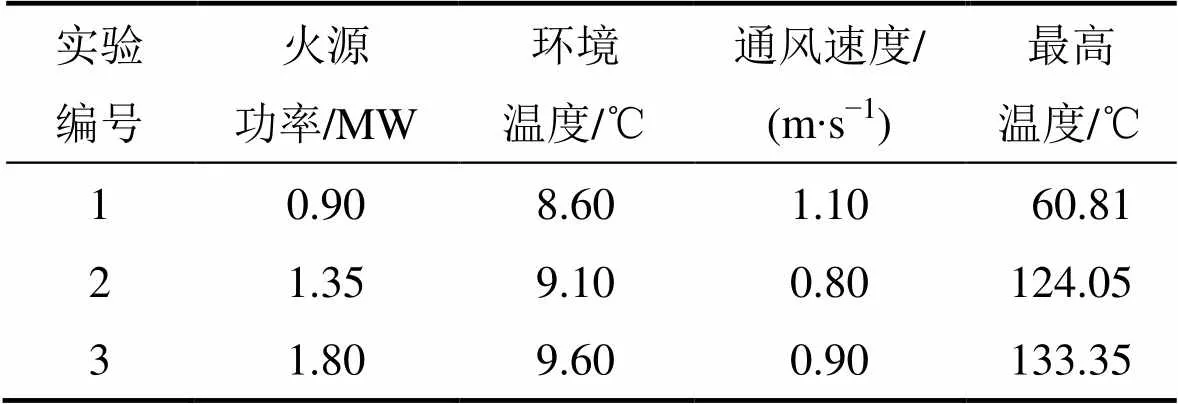
表5 全尺寸模型实验方案及其最高温度

3.5 结果分析

3.5.1 最高温度预测模型的验证

图8所示为相似模型实验以及全尺寸实验的最高烟气温度结果。从图8可以看出：模型实验以及全尺寸实验结果和式(7)结果吻合，从而验证断面形状系数0.63＜＜1的隧道的最高温升计算公式是正确的。也就是说，当断面形状系数小于1时，隧道宽度小于高度，火源卷吸空气受到限制，因而烟气发展受到限制，从而隧道顶部最高烟气温度相对较低。

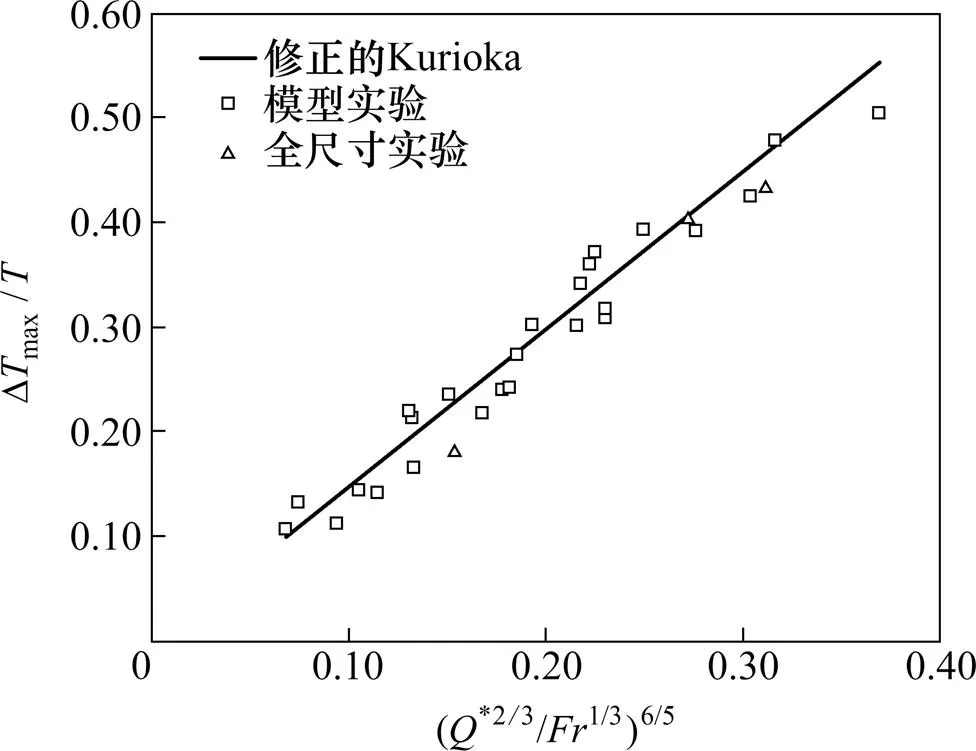
图8 修正的Kurioka模型与相似模型实验及全尺寸实验对比

3.5.2 烟气纵向温度分布规律的验证

将隧道顶棚上游温度纵向分布修正式(10)所得结果与相似模型实验结果进行对比。把相似模型隧道断面形状系数=0.89代入修正式(10)，将相似模型实验结果整理为无量纲温升与无量纲距离的关系。修正的烟气纵向温度分布与相似模型实验结果对比如图9所示。从图9可以看出：修正式(10)与相似模型实验结果吻合程度较好。因此，对于隧道断面形状系数小于1的隧道，顶棚上游温度纵向分布可以用式(10)表示。

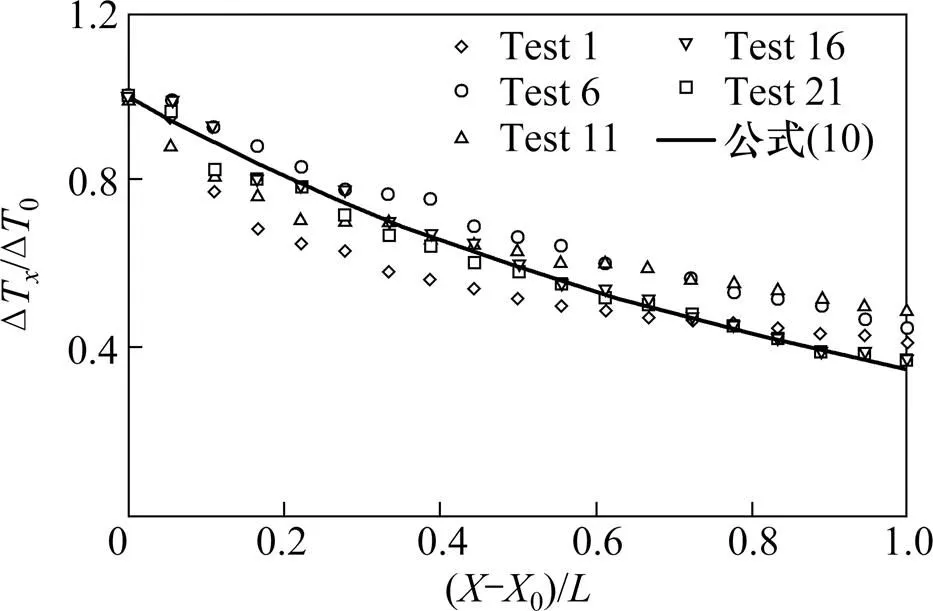
图9 修正的烟气纵向温度分布与相似模型实验结果对比

4 结论

1) 单洞单向隧道断面形状系数为0.63~0.97，单洞双向隧道断面形状系数为1.01~1.85。

2) 对于断面形状系数≥1的地铁区间隧道，可以采用Kurioka模型预测隧道顶部烟气最高温度；对于断面形状系数＜1的地铁区间隧道，需要对Kurioka模型进行修正，隧道顶部烟气最高温升比Kurioka模型小，修正系数=1.51。

3) 对于断面形状系数≥1的地铁区间隧道，顶棚上游烟气温度沿纵向成指数衰减规律；对于断面形状系数＜1的地铁区间隧道，随着隧道断面形状系数的增大，隧道顶棚上游烟气温度沿纵向衰减速率增加；通过引入断面形状系数对顶棚温度沿程衰减模型进行修正，获得修正值与断面形状系数之间的线性表达式。

4) 由于实验条件的限制，对于断面形状系数＜1的隧道顶部最高温度的计算，仅讨论了火源功率较小的情况。因而，需要进一步开展实体实验，探讨较大火源功率的情况，以此验证修正公式的准确性。

[1] WENG Miaocheng, YU Longxing, LIU Fang, et al. Full-scale experiment and CFD simulation on smoke movement and smoke control in a metro tunnel with one opening portal[J]. Tunneling and Underground Space Technology, 2014, 42(5): 96−104.

[2] Li J S M, Chow W K. Illegal carriage of dangerous goods and their effects on tunnel safety[J]. Tunnelling and Underground Space Technology, 2000, 15(2): 167−173.

[3] Leitner A. The fire catastrophe in the Tauern Tunnel: experience and conclusions for the Austrian guidelines[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 217−223.

[4] Vuilleumier F, Weatherill A, Cransaz B. Safety aspects of railway and road tunnel: example of the Lötschberg railway tunnel and Mont-Blanc road tunnel[J]. Tunnelling and Underground Space Technology, 2002, 17(2): 153−158.

[5] Yasuda F, Ono K, Otsuka T. Fire protection for TBM shield tunnel lining[J]. Tunnelling and Underground Space Technology, 2004, 19(4/5): 317.

[6] Lee S R, Ryou H S. A numerical study on smoke movement in longitudinal ventilation tunnel fires for different aspect ratio[J]. Building and Environment, 2006, 41(6): 719−725.

[7] Li Y Z, Lei B, Ingason H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires Original Research Article[J]. Fire Safety Journal, 2011, 46(4): 204−210.

[8] Blanchard E, Boulet P, Desanghere S, et al. Experimental and numerical study of fire in a midscale test tunnel[J]. Fire Safety Journal, 2012, 47:18−31.

[9] Kurioka H, Oka Y, Satoh H, et al. Fire properties in near field of square fire source with longitudinal ventilation in tunnels[J]. Fire Safety Journal, 2003, 38(4): 319−340.

[10] 彭伟, 霍然, 胡隆华, 等. 隧道内纵向风速对火源上方烟气温度影响的实验[J]. 中国科学技术大学学报, 2006, 36(10): 1063−1068.
PENG Wei, HUO Ran, HU Longhua, et al. Smoke temperature near the tunnel ceiling and above the fire source at different longitudinal ventilation velocities[J]. Journal of University of Science and Technology of China, 2006, 36(10): 1063−1068.

[11] Hu L H, Huo R, Peng W, et al. On the maximum smoke temperature under the ceiling in tunnel fires[J]. Tunnelling and Underground Space Technology, 2006, 21(6): 650−655.

[12] 袁建平, 方正, 黄海峰, 等. 水平隧道火灾通风纵向临界风速模型[J]. 土木建筑与环境工程, 2009, 31(6): 67−70.
YUAN Jianping, FANG Zheng, HUANG Haifeng, et al. Model of critical velocity for fire ventilation in horizontal tunnels[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(6): 67−70.

[13] 易亮, 杨洋, 徐志胜, 等. 纵向通风公路隧道火灾拱顶烟气最高温度实验研究[J]. 燃烧科学与技术, 2011, 17(2): 109−114.
YI Liang, YANG Yang, XU Zhisheng, et al. Maximum temperature of smoke near vault in road tunnel fires with longitudinal ventilation[J]. Journal of Combustion Science and Technology, 2011, 17(2): 109−114.

[14] Atkinson G T, Wu Y. Smoke control in sloping tunnels[J]. Fire Safety Journal, 1996, 27(4): 335−341.

[15] 姜学鹏, 胡杰, 徐志胜, 等. 铁路隧道火灾烟气逆流的计算模型[J]. 中南大学学报(自然科学版), 2011, 42(9): 2837−2842.
JIANG Xuepeng, HU Jie, XU Zhisheng, et al. Computation model for back-layering flow of fire smoke in railway tunnel[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2837−2842.

[16] Hu L H, Chen L F, Wu L, et al. An experimental investigation and correlation on buoyant gas temperature below ceiling in a slopping tunnel fire[J]. Applied Thermal Engineering, 2013, 51(1/2): 246−254.

[17] Hu L H, Huo R, Li Y Z, et al. Full-scale burning tests on studying smoke temperature and velocity along a corridor[J]. Tunneling and Underground Space Technology, 2005, 20(3): 223−229.

[18] Hu L H, Huo R, Wang H B, et al. Experimental studies on fire-induced buoyant smoke temperature distribution along tunnel ceiling[J]. Building and Environment, 2007, 42(11): 3905−3915.

[19] Chow W K, Wong K Y, Chung W Y. Longitudinal ventilation for smoke control in a tilted tunnel by scale modeling [J]. Tunnelling and Underground Space Technology, 2010, 25(2): 122−8.

[20] Kevin M G, Randall M D, Simo H, et al. Fire Dynamics Simulator (Version 5) User’s Guide[M]. Washington: U.S. Government Printing Office, 2010: 35.

Smoke temperature distribution on the top of underground metro tunnel

LIU Fang1, 2, 3, WENG Miaocheng1, 2, 3, YU Longxing1, LI Gang1, LIAO Shujiang4

(1. Faculty of Urban Construction and Environmental Engineering, Chongqing University, Chongqing 400045, China;2. Key Laboratory of the Three Gorges Reservoir Region’s Eco-Environment,Ministry of Education, Chongqing University, Chongqing 400045, China;3. National Centre for International Research of Low-carbon and Green Buildings,Chongqing University, Chongqing 400045, China;4. Fire Department of Chongqing Municipal Public Security Bureau, Chongqing 401121, China)

Based on the investigation of the metro tunnel section of Line 6 in Chongqing, China, sectional coefficientwas introduced to describe geometrical characteristic of tunnel section. The smoke temperature distribution on the top of the tunnels with induced longitudinal flow under different HRR and longitudinal ventilation velocity was researched by small scale model experiments and FDS simulations methods. The results show that Kurioka model can be used in the tunnel with≥1, and it should be modified for the tunnel with＜1. And the smoke temperature rise along longitudinal direction corresponds exponential decay law in the tunnel with≥1, and it should be also modified for the tunnel with＜1. The relationship between modification valueKand the sectional coefficient ζ is linear, and the decay speed increases with the increase of.

safety engineering; metro tunnel fire; smoke temperature; scale model experiment; numerical simulation

X928.03；U459.2

A

1672−7207(2015)02−0661−09

2014−02−20；

2014−05−15

高等学校学科创新引智计划项目(B13041)；重庆市研究生科研创新项目(CYB14031)(Project (B13041) supported by the Program of Introducing Talents of Discipline to University; Project (CYB14031) supported by Chongqing Graduate Student Research Innovation Program)

翁庙成，博士研究生，从事建筑防火技术，建筑节能与室内热湿环境研究；E-mail：mcweng@126.com

10.11817/j.issn.1672-7207.2015.02.039

(编辑 赵俊)