城市公路隧道火灾近火源区长度的研究*

李垣志，牛国庆，张轩轩

(河南理工大学 安全科学与工程学院，河南 焦作 454000)

数字出版日期： 2017-12-22

0　引言

随着我国城市人口的不断增加，地面交通状况严重恶化，为缓解地面交通压力，城市隧道得到了飞速发展。截止2016年底，全国公路隧道为15 181处、1 403.97万米，比2015年新增1 175处、135.58万米，其中特长隧道815处、362.27万米，长隧道3 520处、604.55万米[1]。隧道是一个狭长受限空间，一旦发生火灾将给人们的生命及财产带来较大损失[2]。统计结果表明[3]，火灾中超过85%的人员伤亡都是由烟气造成的。因此，准确的掌握隧道烟气蔓延规律对制定排烟方案和现场指导人员疏散具有重要的意义。

隧道烟气蔓延过程大致划分为4个阶段[4-5]：羽流上升阶段、径向蔓延阶段、过渡阶段和一维水平蔓延阶段，其中前3个阶段为近火源区，定义由过渡阶段转入一维蔓延阶段的起始位置距火源中心的距离为近火源区长度，亦作三维扩散距离，如图1所示。

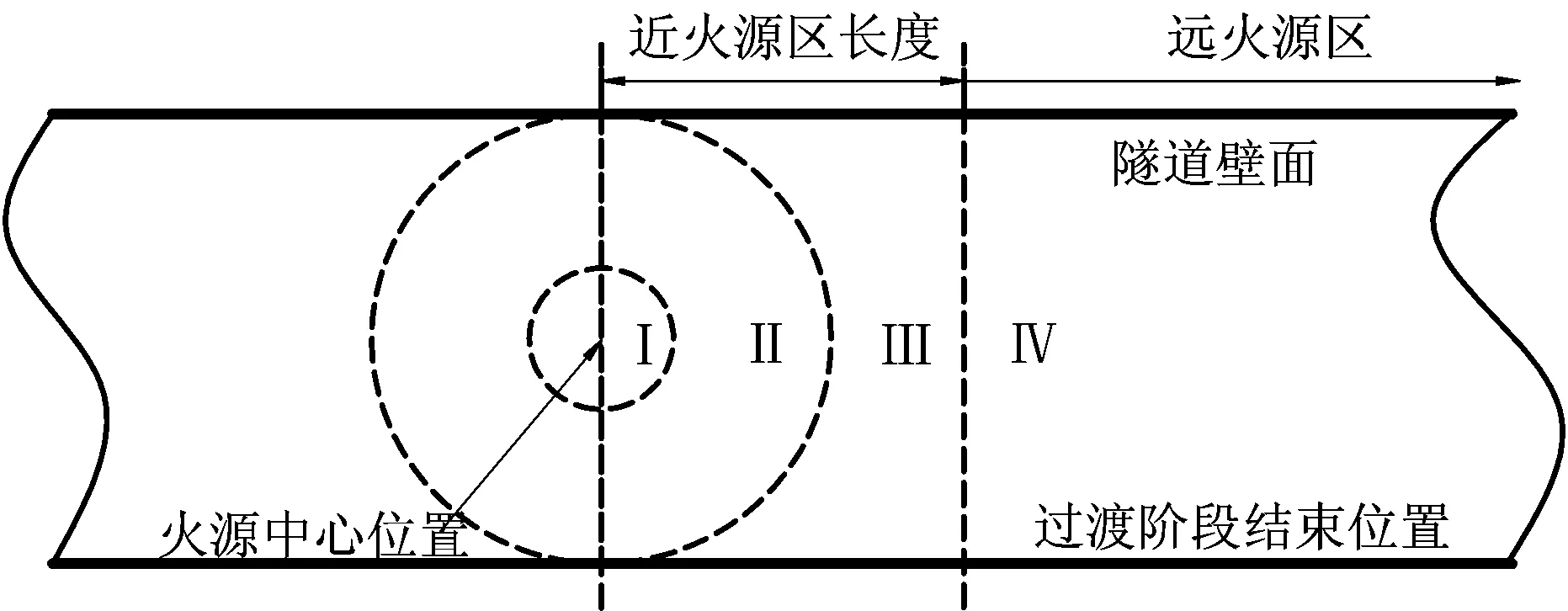
注：Ⅰ～Ⅳ分别表示烟气蔓延的4个阶段。图1　近火源区长度示意Fig.1　Sketch map of the length of near fire source field

烟气在不同阶段表现出不同的流动特性，在研究有关各阶段烟气热物特性问题时，需要对不同阶段的起始位置进行明确划分，其中，对第3，4阶段的划分尚不明确，有关该问题的研究也比较匮乏。纪杰[6]等根据一维水平蔓延阶段烟气的温度分布特性，找出了烟气由过渡阶段转入一维蔓延阶段的位置，认为火源功率大小对该位置没有影响。但研究中所采用火源功率较小，火焰并未撞击顶棚，针对隧道火灾中的大火源功率该结论是否适用仍有待研究；李炎峰[7]等利用大涡模拟手段探究了隧道断面尺寸、火源功率和火源热释放速率对近火源区长度的影响，结果表明：隧道尺寸和火源功率对该长度影响不大，火源发展规律对该长度影响较大；袁中原[8]通过搭建隧道火灾模型试验台，开展顶部开孔的地铁区间遂道火灾模型试验，分析了隧道火灾时烟气扩散形态和羽流发展特性，认为当火源与侧壁距离减小和隧道坡度增大时，烟气一维扩散的起始位置离火源较远，即近火源区长度增大。

虽然前人对近火源区长度进行了探究，并取得了一定的成果，但对该问题的研究还不够完善，也没有提出相关的预测模型。因此，本文通过理论分析和数值模拟的方法对近火源区长度进行了探究，目的在于准确掌握烟气从过渡阶段转入一维蔓延阶段的发展规律，能够为定量研究各阶段烟气流动特性提供参考依据。

1　数值模拟

FDS(fire dynamics simulator)是美国国家标准与技术研究院开发的一种计算流体力学模拟程序，目前为止已有第6个版本，主要用于求解微分方程，可以模拟火灾导致的热量和燃烧产物的低速传输、材料的热解、火焰传播和火灾蔓延、辐射和对流传热等。该软件经过大量的实验验证，具有准确、高效、经济的特点，目前已被广泛应用于火灾动力学研究[2,9-10]。

1.1　模型的建立

根据文献[11]中表1的统计结果，本文选择单孔3车道，宽度为12 m，高度为5.28 m的矩形断面作为公路隧道的代表性尺寸，使模拟结果具有一定的推广性。考虑到计算机性能和时间问题，隧道长度设为80 m足以满足本文要求。为了保证火源不受隧道端部边界条件的影响，将火源布置在距隧道端部30 m处。

图2　FDS模型Fig.2　FDS model diagram

1.2　火源功率确定

为了验证小火源功率和大火源功率对近火源区长度的影响，选用火焰未撞击顶棚和火焰连续撞击顶棚且形成水平扩展火焰的两种火源，根据平均火焰高度计算公式[12]，见式(1)，最终确定火源功率大小，见表1所示。选择正庚烷作为燃料，火源尺寸为1 m×1 m的方形油盆，其他参数采用软件默认。

Η=0.235Q2/5-1.02D

(1)

式中：H为火焰平均高度，m；Q为火源功率，kW；D为火源当量直径，m。

表1　火焰长度计算

1.3　初边条件确定

隧道墙壁材质选择混凝土，隧道两个端部采用开口边界，环境温度为Ta=20 ℃，定压比热容Cp=1.005 kJ/kg·K，空气密度ρa=1.204 kg/m3，重力加速度为g=9.81 m/s2，其他参数均采用软件默认值。

1.4　网格划分

网格尺寸的选取是决定模拟结果是否准确的关键因素。一般认为，网格划分越精细计算结果越准确，所耗费的计算机资源和时间就越多，而在实际应用中，通常采用火源特征直径D*与计算网格尺寸δx的比值作为网格划分的依据，D*的计算公式见式(2)。研究表明[13]，D*/δx的值在4～16之间时，可以得到较好的模拟结果。另外，随着离开火源距离的增大，模拟的准确性对网格的精细程度要求越低[14]。因此，为了在合理的时间内得到准确的模拟结果，选用0.1D*网格的尺寸对火源附近 范围进行加密，其他部分采用0.2D*的网格尺寸。鉴于所确定的火源功率变化较大，分别以较小火源功率(0.8 MW， 6 MW)为标准计算网格尺寸，保证较大火源功率也能满足精度要求。因此，采用两种网格尺寸进行划分，结果见表2和图3所示。

(2)

式中：D*为火源特征直径，m；Q为火源功率，kW；Ta为温度，K；Ca为比热容，kJ/kg·K。

表2　网格划分

图3　网格划分示意Fig.3　Mesh assigned for numerical simulation

1.5　烟气层温度分布特性

烟气在不同蔓延阶段中，温度场表现出不同的分布规律。火源正上方烟气温度最高，随着距火源位置增加，温度呈指数衰减[15-16]。当烟气进入一维水平蔓延阶段时，隧道横断面上的温度场分布较为稳定。图4为Q=6 MW，分别距离火源5，10和30 m处的温度场分布切片。从图中可以看出，在同一水平高度上，随着距火源距离的增加，横向温度场分布逐渐趋于稳定，反浮力壁面射流消失，烟气层厚度不再发生变化，竖向温度场呈明显的分层现象。因此，在一维蔓延阶段，烟气的温度场分布较其他阶段更为均匀、稳定。

图4　隧道断面温度场分布Fig.4　Distribution of temperature field in tunnel section

图5为Q=6MW，距顶棚高度h=0.05，0.8，1.6 m处纵向中心线的温度曲线。设隧道延伸方向为x方向，x=0 m处为火源中心位置。可以看出，不同高度的烟气温度在隧道两端呈对称分布，在0～7 m之间温度急剧下降，大于7 m后开始缓慢下降，温度衰减趋势基本相同，表明不同高度处，烟气的纵向温度衰减趋势呈高度的相似性。

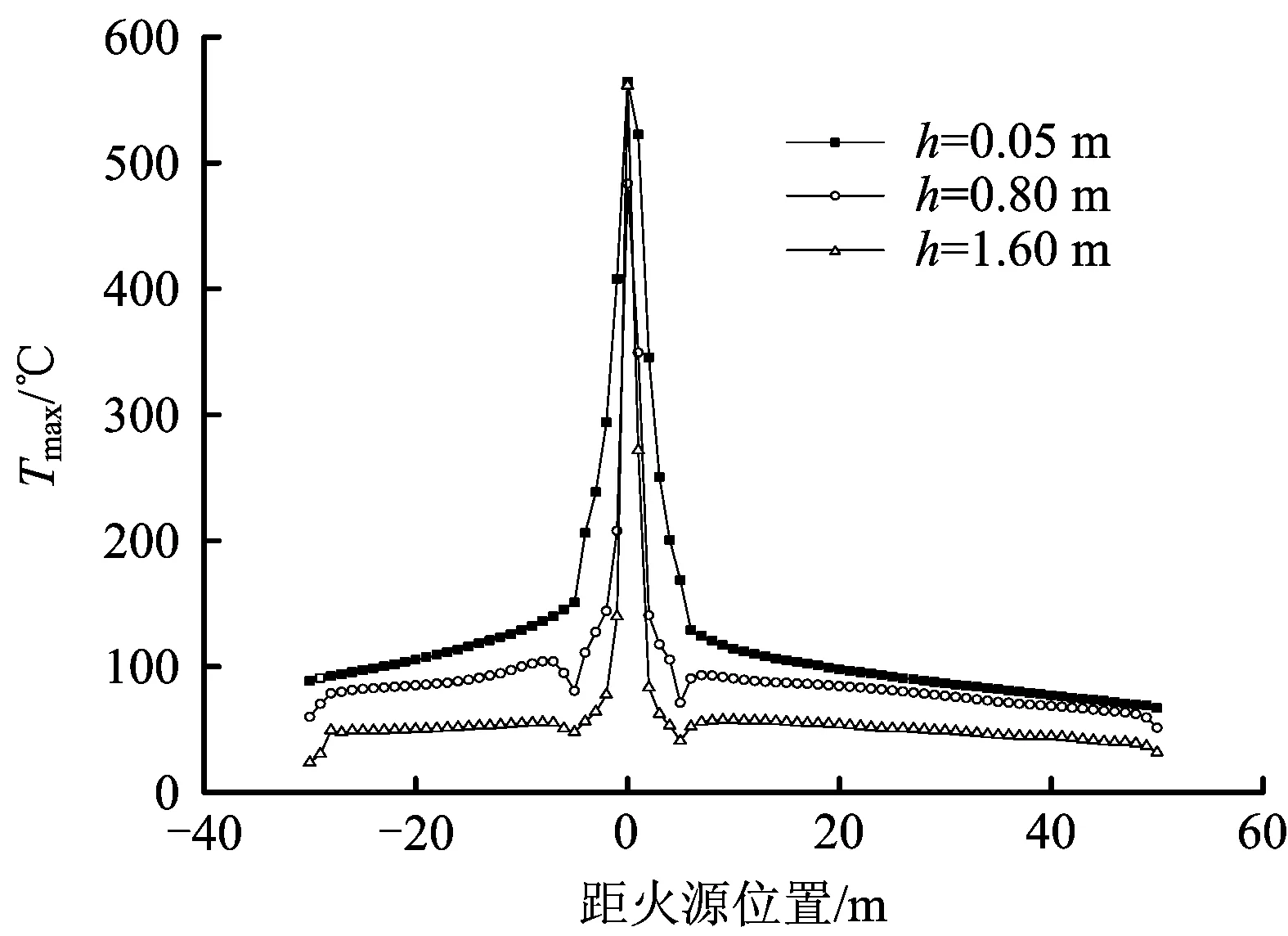
图5　纵向中心线温度分布曲线Fig.5　Longitudinal centerline temperature distribution curve

图6　不同水平中心线与侧壁温度分布曲线Fig.6　Temperature distribution curve of different horizontal center and side wall

图6为Q=6 MW，烟气在h=0.05，0.8和1.6 m处，侧壁与纵向中心线的温度衰减曲线。可以看出，在同一高度上，随着距火源距离的增加，同一截面上两测点温差逐渐减小，最终落入同一个区间内，表明烟气进入了一维蔓延阶段。在不同高度上烟气进入一维蔓延阶段的位置有所不同，这主要是侧壁温度衰减速率不同引起的，当h=0.05 m时，侧壁温度衰减较慢，x=13 m时开始稳定衰减；h=1.6 m时，侧壁温度急剧下降，x=6 m时开始稳定衰减；h=0.8 m时介于二者之间。这是由于烟气层下部烟气与冷空气发生卷吸所用，导致烟气层温度迅速下降，而烟气层上部烟气温度较高，不与空气接触，温差小，能量交换少，温度衰减相对较慢，因此，进入一维蔓延阶段的位置就会向后推移。

根据上述分析，当火源位于隧道中部时，由于矩形断面隧道在纵向和横向尺度上的对称性，在保证火源不受隧道开口边界条件影响下，只考虑隧道一端和一侧的烟气温度分布情况，又因下部烟气进入一维蔓延阶段的位置较上部烟气提前，因此，只考虑火源一侧且距顶棚高度为0.05 m位置处的烟气温度情况。

1.6　热电偶布置

根据前节分析，在h=0.05 m处沿隧道纵向布置5串热电偶，每串热电偶间隔3 m，火源附近 范围内热电偶间隔为0.25 m，其他位置间隔为0.5 m，测点布置如图7所示。

图7　测点布置示意Fig.7　Sketch map of layout of measuring points

2　量纲分析

便于量纲分析，首先考虑火源位于隧道中部时，火源功率Q和有效顶棚高度Hef(油盆表面距顶棚的高度，m)对近火源区长度的影响。设近火源区长度为LC，分别与Q，Hef，Ta，ρa，g，Cp6个变量有关，见式(3)所示，基本量纲为L，M，T，θ(时间)，选择Hef，Ta，ρa，g作为循环变量，分别与其余变量组成无量纲数组π1，π2，π3，a0～d2为待定系数。

f(LC,Q,Hef,Ta,ρa,g,Cp)=0

(3)

其中：

(4)

(5)

(6)

因π1，π2，π3为无因次数组，使得等式右边的基本量纲因次为0，最终计算结果为：

(7)

(8)

(9)

有

f(π1,π2,π3)=0

(10)

将π3移至左边，并将π2带入π1消去Hefg有：

(11)

定义火源位于隧道中部时无量纲近火源区长度LC*和无量纲火源功率Q*：

(12)

(13)

故

(14)

可以看出LC*与Q*存在一定的关系，因此，本文采用数值模拟的方法对这种关系进行探究。

3　结果与分析

3.1　模拟工况

根据量纲分析的结果，首先考虑火源位于中部时火源功率和有效顶棚高度对近火源区长度的影响，再考虑火源横向位置对长度的影响，因此，需要设计2个系列的工况进行模拟：系列1为探究火源功率和有效顶棚高度对近火源区长度的影响，其中工况1为小功率火源作为对照组，工况2～4分别为改变火源功率和有效顶棚高度；系列2为同一火源功率下，分别改变火源的横向位置(火源中心距近侧壁的距离，用d表示，m)的工况，具体模拟工况如表3所示，总模拟时间为100 s，测点温度为烟气处于稳态时的平均值。

3.2　火源功率对近火源区长度的影响

(15)

式中：DTij为i热电偶串中第j个热电偶位置的温度梯度值，℃/m，i取1～5对应图7中A～E，j=1,2,3,…,171；n为热电偶间隔距离，m，j≤21时，n=0.25 m，j>21时，n=0.5 m。

(16)

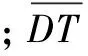
表3　数值模拟工况

(17)

图8　不同火源功率温度分布曲线Fig.8　The temperature distribution curve of different fire sources

图8中(a)和(b)分别为Q=0.8 MW和2 MW时，侧壁、中心线及二者之间位置的温度分布曲线。可以看出，在近火源区，中心线温度衰减最快，侧壁最慢，中间温度衰减介于二者之间，且最先与中心线温度曲线重合。当x=11 m时，α小于1 ℃/m，当x>11 m时，三条曲线基本重合，温度衰减趋于一致，可以认为烟气进入了一维蔓延阶段，Q=2MW时也具有相同的分布特点。这是由于当火源功率较小时，烟气与隧道壁面及空气之间的热交换成为烟气温度变化的主要方式，近火源区中心线上的温度越高，与周围介质的温差越大，温度衰减就越快，而侧壁烟气温度越低，与周围介质温差越小，温度衰减就越慢，因此，二者在远离火源一定距离后温度衰减速率几乎相同，当烟气温度受火源影响很小时，改变火源功率，对热烟气温度衰减速率影响不大，进入一维蔓延阶段的位置不发生明显变化，近火源区长度基本保持不变。

图8中(c)和(d)分别为Q=6 MW和14 MW时的温度分布曲线。可以看出，增大火源功率时，烟气进入一维蔓延阶段位置发生了变化。Q=6 MW时，x=12.5 m，较小火源功率向后推移1.5 m，当Q=14 MW时，位移继续增加(x=19.5 m)。为了解释这一现象，图9给出了Q=0.8，2，6和14 MW时纵向中心线温度梯度衰减曲线，取温度降低方向为正方向，可以看出，在近火源区，大火源功率的温度梯度和变化幅度明显高于小火源功率；随着距离的增加，远火源区的温度梯度基本保持恒定，但进入稳定衰减阶段的位置有所不同，这是由于火源功率的增加导致火源特征直径和水平扩展火焰长度也随之增加，从而扩大了火源的影响范围，在该范围内，水平蔓延的烟气温度变化除了受隧道壁面和空气温度的影响，还受火焰辐射和热对流因素的影响，当烟气远离水平扩展火焰一定距离时，烟气温度几乎不受火焰影响，开始进入稳定衰减阶段，同时考虑其他位置的温度变化情况，从而进一步判断是否进入一维蔓延阶段。

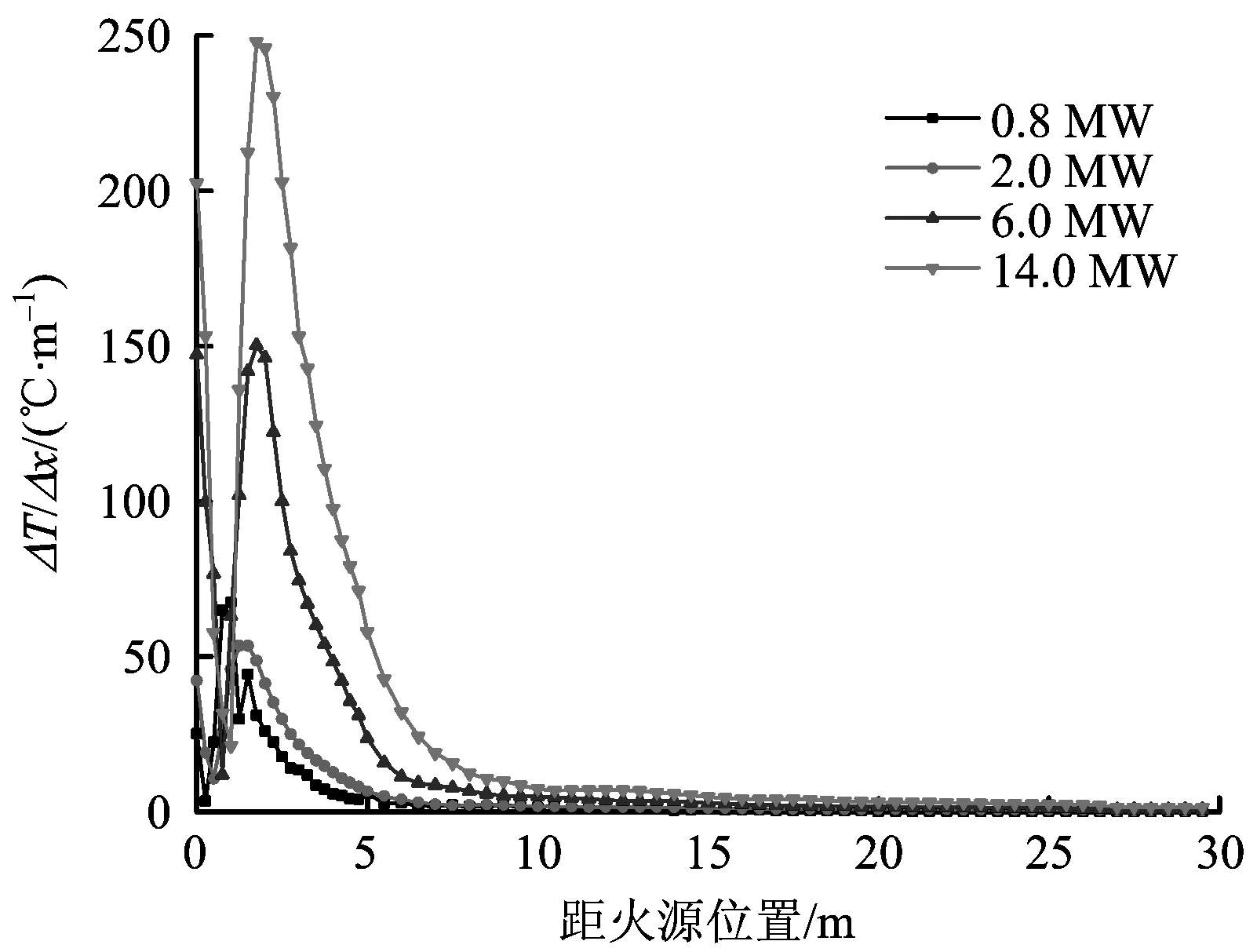
图9　纵向中心线温度梯度变化曲线Fig. 9　Vertical centerline temperature gradient curve

图10为Q=2，6和14 MW时顶棚受火源热辐射的影响范围，可以看出Q=14 MW的热辐射范围最大，6 MW次之，2 MW最小，进一步表明随着火源功率的增加，火源的影响范围逐渐扩大，强度增强。

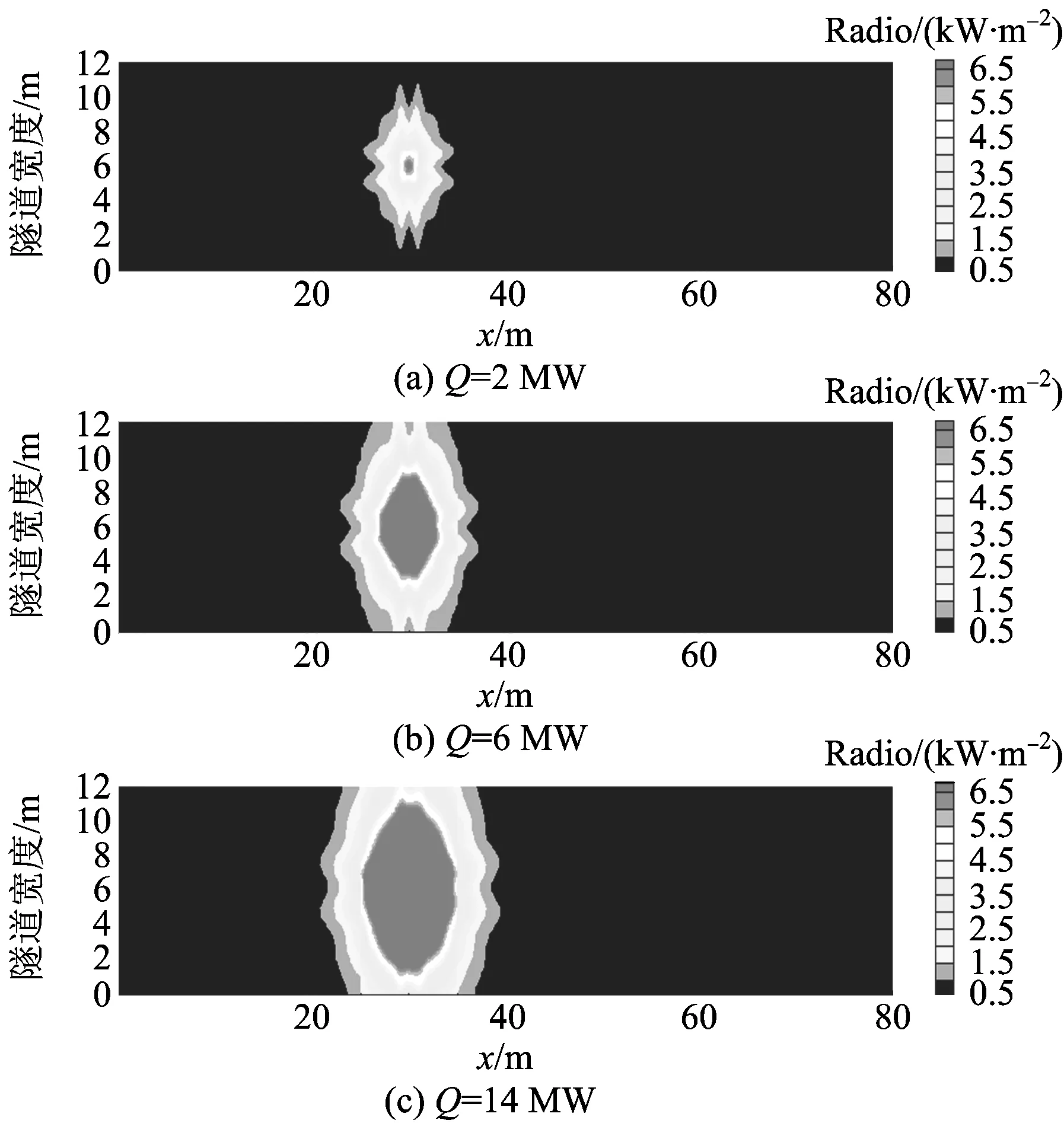
图10　辐射范围Fig.10　Radiation range

图11　有效顶棚高度对近火源区长度的影响Fig.11　The influence of effective ceiling height on the length of near fire zone

根据上述分析，保持火源功率不变，减小有效顶棚高度，水平扩展火焰继续延伸，对顶棚烟气温度的影响进一步扩大，进而导致近火源区长度继续增加。图11为有效顶棚高度为4.78 m，功率为14 MW时的温度衰减曲线，可以看出，比Hef=5.28 m时增加了1.5 m。

系列1工况的模拟结果如表4所示。图12为火源位于隧道中部时，无量纲近火源区长度LC*与无量纲火源功率Q*的2/3次方的关系图。

表4　系列1工况模拟结果

图12　无量纲近火源区长度与无量纲火源功率的关系Fig.12　Relationship between dimensionless length of near fire zone and dimensionless fire source power

从图12可以看出，系列1中15个点都位于一条过原点的直线附近，因此，可以把LC*和Q*2/3之间的关系表示为：

(18)

从拟合相关系数R2和标准误差RMSE可以看出拟合效果较好。

3.3　火源横向位置对近火源区长度的影响

为了进一步探究火源横向位置对近火源区长度的影响，对表3中系列2的18个工况进行模拟。由于火源位置发生变化，烟气温度在横断面上的温度分布不再对称，因此，需要同时考虑所有横断面上的温度分布。图13为火源功率为6 MW，火源中心距侧壁3 m和贴壁时的温度分布曲线。

图13　不同火源横向位置的温度分布曲线Fig. 13　Temperature distribution of different fire sources in transverse position

从图13中可以看出，随着火源横向位置的变化，进入一维蔓延阶段的位置也发生变化，主要受以下两方面因素的影响：

1)远侧壁温度。当火源横向位置发生变化时，火源中心距隧道近侧壁距离减小，远侧壁距离增加，横向温度衰减速率大于纵向温度衰减速率[17]，又因火源的热辐射和对流作用对远侧壁烟气温度影响较小。因此，远侧壁烟气温度越低，温度衰减就越慢，而火源正上方的温度衰减速率较火源位于隧道中部时变化不大，导致进入一维蔓延阶段的位置向后推移。

2)火焰纵向扩展长度。据前人研究结果表明[11]：当火源贴壁时，火焰纵向扩展长度大于横向长度，大于火源位于隧道中部时的长度。因此，火源贴壁时，近火源区长度达到最大。

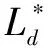
(19)

式中：Ld为火源横向位置变化时近火源区长度，m。

(20)

计算结果见表5，图14为无量纲横向位置d*和无量纲近火源区长度L**的关系。

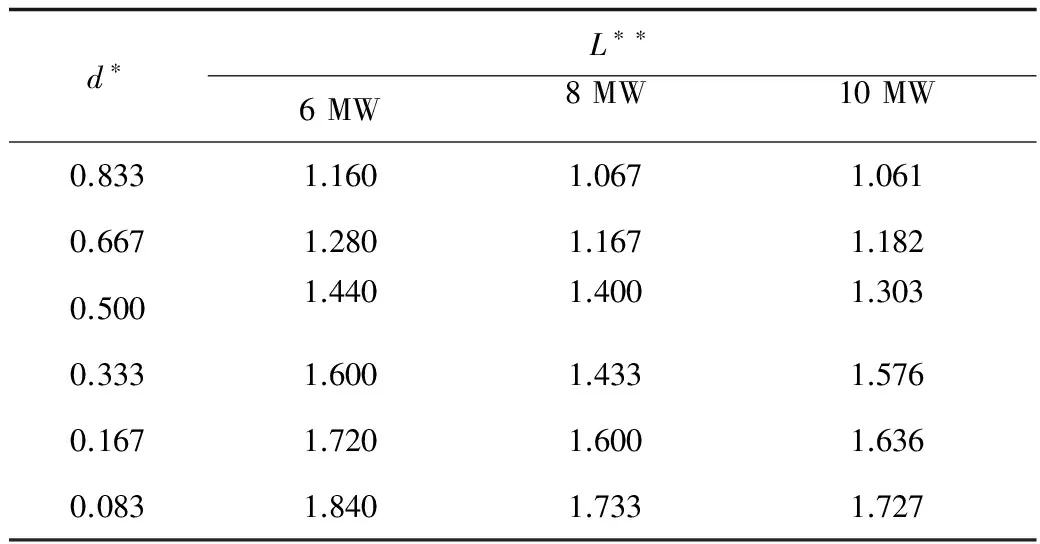
表5　系列2工况模拟结果

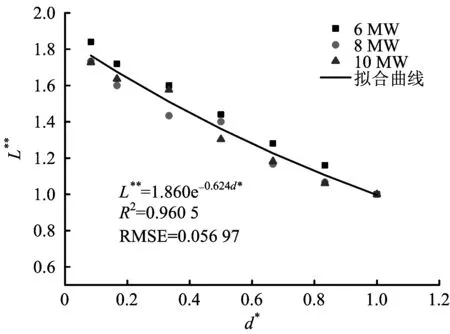
图14　无量纲近火源区长度与无量纲火源横向位置关系Fig. 14　Relationship between dimensionless length of nearfire zone and lateral position of dimensionless fire source

由图14可以看出，无量纲横向位置d*和无量纲近火源区长度L**成自然指数关系，通过拟合可以得到如下关系。

L**=1.860 exp(-0.624d*)

(21)

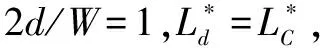
(22)

式(22)是关于火源横向位置、有效顶棚高度、火源功率与近火源区长度的函数关系式，可以用于描述火焰连续撞击顶棚时，近火源区长度随火源功率、有效顶棚高度和火源横向位置变化的规律。

本文主要探究上述3个因素对近火源区长度的影响，故在数值模拟中对初边界条件做出了一定的假设，未考虑自然风、活塞风和隧道坡度等因素的影响，因此，所得结论与实际隧道存在一定的差异，仅适用于与模拟条件相近的情况。

4　结论

1)当火源功率较小，火焰未撞击顶棚时，改变火源功率对近火源区长度几乎没有影响；当火源位于隧道中部，并产生水平扩展火焰时，无量纲近火源区长度与无量纲火源功率的2/3次方呈线性关系；当火源横向位置发生变化时，随着火源与侧壁距离的减小，近火源区长度呈自然指数增长趋势；当火源贴壁时，近火源区长度是火源位于中部时的1.866倍；

2)根据理论分析和数值模拟结果，给出了近火源区与远火源区的划分标准，并建立了近火源区长度预测模型，基本揭示了烟气由过渡阶段转入一维蔓延阶段起始位置的变化规律，为定量研究各阶段烟气流动特性提供理论依据。

[1]中华人民共和国交通运输部. 2016年交通运输行业发展统计公报[R]. 中国交通报, 2017-4-17(002).

[2]钟委, 端木维可, 李华琳, 等. 火源横向位置对隧道火灾烟气分岔流动影响[J]. 郑州大学学报(工学版), 2017, 38(1): 27-31.

ZHONG Wei, DUAN Muweike, LI Hualin, et al. Numerical investigation into the influence of different transverse fire locations on smoke bifurcation flow in tunnel fire[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(1): 27-31.

[3]HU L. H., ZHOU J. W., HUO R., et al. Confinement of fire-induced smoke and carbon monoxide transportation by air curtain in channels.[J]. Journal of Hazardous Materials, 2008, 156(1-3): 327-334.

[4]纪杰. 地铁站火灾烟气流动及通风控制模式研究[D]. 合肥: 中国科学技术大学, 2008.

[5]钟委. 地铁站火灾烟气流动特性及控制方法研究[D]. 合肥: 中国科学技术大学, 2007.

[6]纪杰, 霍然, 张英, 等. 长通道内烟气层水平蔓延阶段的质量卷吸速率实验研究[J]. 中国科学技术大学学报, 2009, 39(7): 738-742.

JI Jie, HUO Ran, ZHANG Ying, et al. Experimental study on the entrainment mass flow rate across the smoke layer interface during horizontal spread in a long channel[J]. Journal of University of Science and Technology of China, 2009, 39(7): 738-742.

[7]李炎锋, 赵威翰, 边江, 等. 城市地下长直隧道火灾近火源区长度确定[J]. 广西大学学报(自然科学版), 2016, 41(4): 1101-1108.

LI Yanfeng, ZHAO Weihan, BIAN Jiang, et al. Length of near field of fire sourcein urban long straight underground tunnel[J]. Journal of Guangxi University(Nat Sci Ed), 2016, 41(4): 1101-1108.

[8]袁中原. 顶部开孔的地铁隧道火灾烟气扩散特性及控制方法[D]. 成都: 西南交通大学, 2012.

[9]高云骥, 朱国庆. 火羽流轴向温度大涡模拟与实验比较[J]. 消防科学与技术, 2014, 33(8): 857-859.

GAO Yunji, ZHU Guoqing. Comparing the model and simulation results of fire plume axial temperature[J]. Fire Science and Technology, 2014, 33(8): 857-859.

[10]黄亚东, 吴珂, 黄志义, 等. 长隧道火灾中拱顶温度场的数值模拟[J]. 消防科学与技术, 2009, 28(4): 162-165.

HUANG Yadong, WU Ke, HUANG Zhiyi, et al. Modeling on temperature field of arch crown in long tunnel fires[J]. Fire Science and Technology, 2009, 28(4): 162-165.

[11]高子鹤. 隧道内受限火羽流行为特征及竖井自然排烟机理研究[D]. 合肥: 中国科学技术大学, 2016.

[12]KARLSSON B., QUINTIERE J. G. Enclosure fire dynamics[M]. CRC press，2002.

[13]吕金金. 纵向风作用下城市隧道火灾烟气分岔流动特性研究[D]. 郑州: 郑州大学, 2014.

[14]周庆. 网格划分对FDS火灾模拟结果的影响分析[J]. 安全, 2011(8): 8-11.

ZHOU Qing. Influence of mesh grid on fire simulation results of FDS[J]. Safety, 2011(8): 8-11.

[15]胡隆华. 隧道火灾烟气蔓延的热物理特性研究[D]. 合肥: 中国科学技术大学, 2006.

[16]JI J., FAN C. G., ZHONG W., et al. Experimental investigation on influence of different transverse fire locations on maximum smoke temperature under the tunnel ceiling[J]. International Journal of Heat and Mass Transfer, 2012, 55(17-18): 4817-4826.

[17]FAN C. G., JI J., GAO Z. H., et al. Experimental study on transverse smoke temperature distribution in road tunnel fires[J]. Tunnelling & Underground Space Technology, 2013, 37(6): 89-95.