渗透压力作用下岩石三轴压缩过程变形特性分析*

肖伟晶，王晓军, 2，李士超，于正兴，黄广黎, 闫　奇

(1.江西理工大学 资源与环境工程学院，江西 赣州 341000；2.江西省矿业工程重点实验室， 江西 赣州 341000；3.中国安全生产科学研究院，北京 100012)

数字出版日期： 2017-12-19

0　引　言

岩石通常是能源储存、核废料处理、水利水电、地下交通和地下矿山等工程的主要介质和地质环境[1-2]，该类地下工程岩体受开挖扰动后，所处应力状态遭到破坏，引起应力重新分布[3]，扰动后的围压将向临空面发生位移变形，因此研究岩体变形特性对工程岩体灾害分析与防治具有重要意义[4-6]。

近年来，国内外关于岩石变形及强度特性的研究从未间断，也取得了丰硕的研究成果。刘俊新[7]等对页岩展开了不同围压及不同应变速率下的三轴压缩试验，分析并研究了应变速率对强度、应变和弹性模量的影响；Bieniawshi等[8]和Peng等[9- 10]分别对细砂岩和凝灰岩等开展不同应变速率下的岩石力学试验；马建林等[11]对盐岩展开三轴循环加、卸载试验，研究了循环荷载对盐岩变形演化的影响；K. Fuenkajorn等[12]通过对盐岩进行单轴循环加卸荷试验，研究周期荷载对盐岩单轴抗压强度、弹性及不可逆变形的影响，研究结果表明，岩石的变形模量和应变受循环次数的影响是有限的；杨春和等[13]对岩石展开单轴循环加、卸载力学试验，研究了岩石的变形特性，研究结果表明循环加卸载能够强化岩石的变形特性；此外，苏承东[14]，杨圣奇[15]等分别对岩石展开三轴压缩试验，针对岩石三轴压缩过程中的变形与能量特征进行了相关研究。综上所述，已有的研究结论为深入探索岩石变形和强度特性奠定了基础。但是，关于渗流-应力耦合作用下岩石的变形和强度特性的研究则鲜有报道。

基于此，笔者对红砂岩展开了恒定围压不同渗压下的三轴压缩试验，分析了不同渗透压力作用下岩石三轴压缩过程中轴向应变、径向应变和变形模量的变化规律，研究结果为探讨类似工程岩体渗透压力作用下的变形特性提供参考。

1　试样制备及方案

1.1　试样制备

红砂岩为第三系、白垄系内陆河湖相沉积岩，在我国华东(江西、安徽、福建) 和中南( 湖南、湖北、广东) 及西南( 四川)等地区均有广泛分布。该类岩石外观呈红色、深红色或红褐色，主要成分为石英、白云母、长石及少量矿物。本试验选用赣南红砂岩为试验试样，考虑到岩石性状的离散性，为使各试样的物理性质具有一致性和试验结果的可比性，钻取同一岩石上相邻部位的岩芯进行加工，如图1所示。根据《工程岩体试验方法标准》(GB/T5026 6-2013)以及国际岩石力学学会(ISRM)推荐标准，加工成尺寸为φ50 mm×100 mm的圆柱形试样，并采用岩石切割机和磨石机对试样端面进切割和打磨，使试样两端不平整度小于0.02 mm。所有岩石试样试验前均用水进行饱和处理。

图1　钻孔取样Fig.1　Bore-hole sampling

1.2　试验设备和方案

采用英国GDS公司生产的GDS-VIS三轴流变仪进行渗透压力作用下的三轴压缩试验，如图2所示。该加载系统采用虚拟无限刚度荷载架，可进行单轴压缩、三轴压缩、流变试验以及渗流-应力耦合试验，最大轴向加载载荷为 400 kN,压板最大有效位移行程为100 mm，实验加载速率能够通过计算机进行人为的设置。轴压、围压和渗压的加载分别由3套独立的配套系统进行加载，由轴向和径向LVDT位移传感器分别测量应力加载过程中的轴向位移和径向位移，试验时全程精度达到了0.05%。

将饱和试样用高性能热缩管包裹并安装LVDT应变传感器，确定与试样接触良好后放入三轴仪的压力室内，试样两端用“O”形橡胶圈将试样与压头箍紧，打开试样顶端出水口阀门，并下放加载横梁并拧紧固定；最后封闭压力腔室，待预加载完成后，依次以1 MPa/min的速率加载围压和渗压；待围压和渗压稳定后以0.1 kN/s的速率加载偏应力，直至试样破坏，试验停止。本次试验条件设置为恒定围压不同渗压，因此各试样固定围压8 MPa，设置渗压依次为2，4，6，7 MPa。

图2　GDS-VIS三轴流变仪全貌Fig.2　Total graph of GDS-VIS three axis rheometer

2　试验结果分析

2.1　变形特性分析

根据试验数据绘制各渗透压力作用下岩石应力-应变曲线，如图3。分析图3可知，渗透压力作用下，红砂岩三轴压缩过程的轴向变形大致可分为4个阶段：孔隙裂隙压密阶段、弹性变形阶段、非稳定破裂阶段及破裂后阶段。随着渗透压力的增大，岩石峰值强度减小。

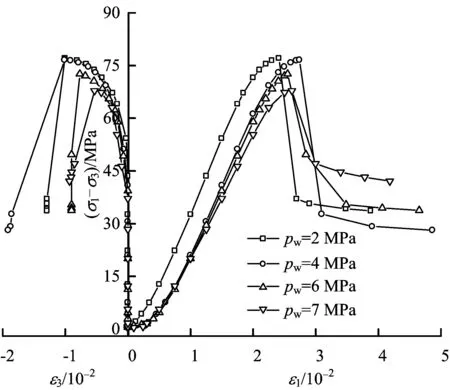
(图中Pw值表示各渗压大小)图3　渗透压力作用下应力-应变曲线Fig.3　Stress strain curves under seepage pressure

分析轴向应变可知，达到峰值应力时，各渗压下岩石的轴向应变ε1c在2.30%～2.74%之间(依次为2.30%，2.74%，2.55%和2.62%)，且随渗压增加，ε1c呈逐渐增大的趋势。与2 MPa渗压相比，4，6，7 MPa渗压下达到峰值应力时轴向应变分别增加了17.8%，10.9%，13.9%；分析径向应变可知，随渗透压力增加，达到峰值应力时，各渗压下岩石径向应变ε3c在-0.535%～-1.012%之间(依次为-1.012%，-1.010%，-0.767%和-0.535%，其中负号表示拉伸变形)，且随渗透压力增加ε3c逐渐减小。与2 MPa渗压相比，4，6，7 MPa渗压下达到峰值应力时径向应变分别减小了0.2%，24.2%和47.1%。

由上述分析可知，与2 MPa渗压相比，随渗压增大，达到峰值应力时的轴向应变的增加幅度在10.9%～17.8%之间，变化幅度较小；达到峰值应力时径向应变减小幅度在0.2%～47.1%之间，与轴向应变相比，变化幅度较大。由此表明，三轴压缩的过程中，较之与轴向应变相比，径向应变对渗透压力变化的敏感性更强，变化幅度较大。

2.2　变形模量分析

由图3可知，随着渗透压力的增大，岩石峰值强度减小，表明渗透水压力的作用能够弱化岩石强度，促进岩样内部裂纹的发育和扩展，诱发岩体失稳。岩石在渗压与应力耦合作用下，产生轴向变形和径向变形，同时变形模量也将随渗透压力的增加而发生改变，为研究各渗压下岩石变形模量的变化规律，其中，变形模量的计算方法有多种，为此，笔者拟采用式(1)进行计算如下[16]：

(1)

式中：E为变形模量，GPa；μ为泊松比；B为某应力状态下岩石的径向应变ε3与其对应的轴向应变ε1的比值；σ1，σ3分别为某应力状态下的轴压和围压，MPa,本次试验为恒定围压下的渗透试验，故σ3取值为8 MPa。

根据式(1)计算得到各渗压下峰值强度时径向应变与轴向应变之比μc，并称之为侧胀系数；峰值强度时变形模量Ec、峰值强度50%时的变形模量E50和泊松比μ50，(见表1)，且随渗压增加，峰值强度、变形模量E50和Ec以及侧胀系数μc均呈减小趋势，分析可知：根据侧胀系数的定义，随渗压增加侧胀系数越小，说明达到破坏时岩石的径向拉伸变形较轴向压缩变形相比逐渐减小。由此表明，渗压的增加能够弱化围压的约束作用，减小岩石承受径向变形的能力，促进岩石发生失稳破坏。

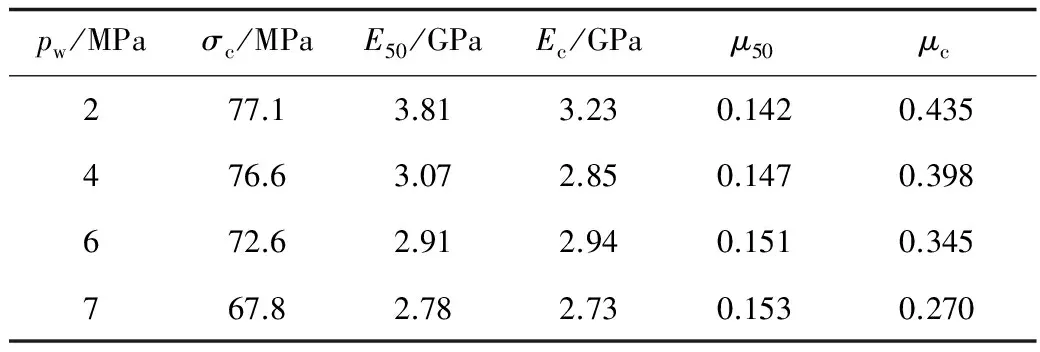
表1　岩石强度参数

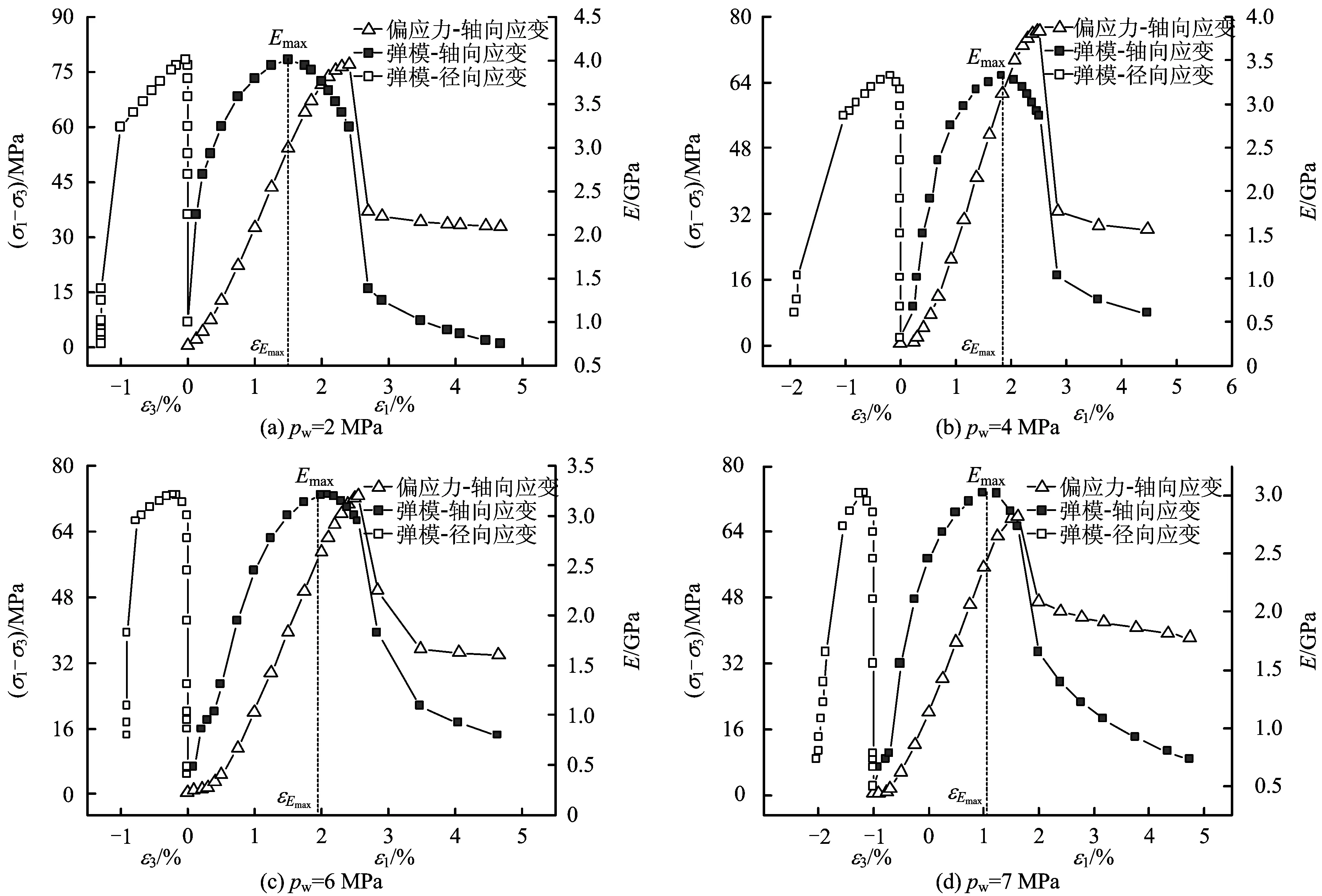
(图中Pw值表示各渗压大小)图4　不同渗压下偏应力、变形模量与应变的关系Fig.4　Relationship between deviatoric stress, deformation modulus and strain under different seepage pressures

根据式(1)计算得到岩石应力-应变过程中变形模量的演化规律，如图4所示。分析图4可知，在偏应力加载初期，岩石处于空隙裂隙压密阶段，此阶段内的岩石变形大多是由空隙裂隙闭合所致，变形模量较小；随着偏应力不断增加，空隙裂隙逐渐压缩闭合，岩样形变主要以岩石颗粒受力变形为主，变形模量逐渐增大；在弹性变形阶段，随岩石试样被持续压缩密实，变形模量减速增加并逐渐趋近于最大值，该最大值为此应力条件下岩石的最大变形模量Emax；在非稳定破裂及破裂后阶段，由于岩石内部非稳定破裂持续发展和贯通，岩石变形快速增加，变形模量逐渐减小，当达到峰值应力后，变形模量呈现“断崖式”下跌，随后逐渐趋于稳定。

进一步分析可知，岩石承载过程中变形模量随偏应力增加而增大，最大变形模量Emax出现在弹性变形阶段后期，如图4，达到屈服应力后变形模量逐渐减小，超过峰值应力后变形模量则骤减。与轴向应变相比，变形模量随径向应变的变化规律则有所差异：在变形模量增加的过程中，径向变形始终较小，当变形模量达到峰值并开始跌落后，径向应变明显增加，表明与轴向应变相比，径向应变则更能反映出岩石变形模量的减小和力学强度的降低。

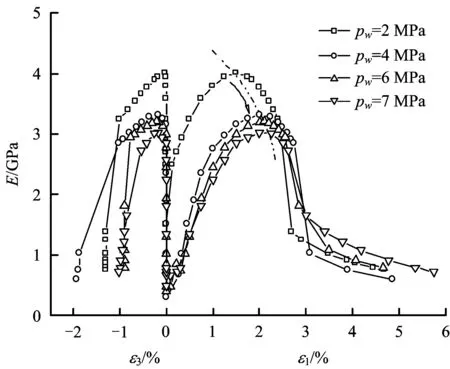
图5　变形模量与应变的关系Fig.5　Relationship between deformation modulus and strain

为分析各渗压下最大变形模量与应力和应变的关系，根据图5，得到各渗压下最大变形模量Emax及其对应的轴向应变εEmax，见表2。

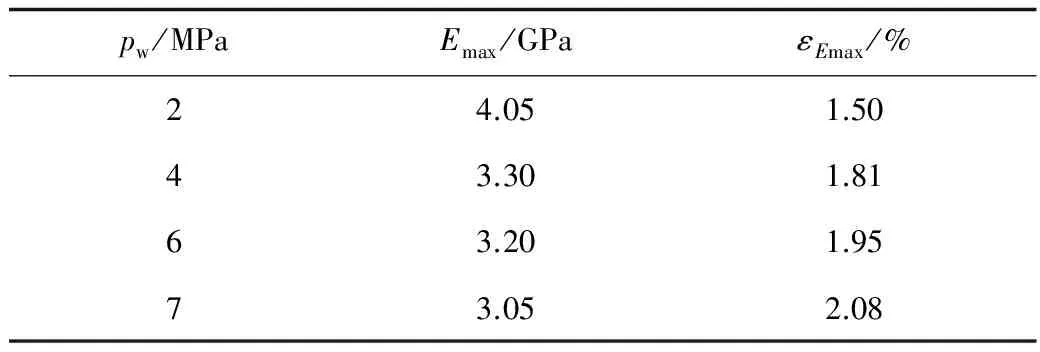
表2　最大变形模量及其对应的应变

由表2分析可知，随渗透压力增加，最大变形模量对应的轴向应变随渗压增大而后移(如图5中箭头所示)。与此同时，渗压越大，岩石承载过程中各变形阶段的变形模量呈减小趋势，其中，与2 MPa渗压相比，4,6,7 MPa渗压下最大变形模量分别降低了0.75， 0.85,1.0 GPa，由此表明，渗透压力能够降低岩石的变形模量。究其原因可知，水在渗透压力作用下，能够在裂隙表面产生润滑作用并增强破裂面上的剪应力效应，同时水的渗入对岩石产生软化、泥化作用，降低岩石力学强度，使岩石的变形模量随渗压增加而降低。

红砂岩是工程实践中常见的工程岩体，在我国有广泛分布。基于本研究的相关结论，可通过实时监测渗透压力作用下岩体变形来分析以红砂岩为主的工程岩体稳定性状况；同时，可根据各渗压下岩石承载过程中变形模量的变化规律来判别不同水压力条件下岩石的失稳和破坏，为分析渗透压力作用下类似岩性的地下工程稳定性提供参考。

3　结论

1)随着渗透压力的增大，岩石峰值应力减小，峰值应力对应的轴向应变量增加，径向应变量则减小，渗透压力作用下岩石承受径向变形的能力随渗透压力的增加而降低。

2)与2 MPa渗压相比，4,6,7 MPa渗压下达到峰值应力时的轴向应变增加幅度在10.9%～ 17.8%之间，径向应变减小幅度在0.2%～47.1%之间，变化幅度较大。表明，与轴向应变相比，径向应变对渗透压力变化的敏感性更强，变化幅度更大。

3)岩石承载过程中，随变形模量的增大径向应变近乎不变，当变形模量开始减小时径向应变则显著增加，表明径向应变能够更明显的反映出岩石承载过程中变形模量的减小和力学强度的降低。

4)岩石承载过程中各变形阶段的变形模量随渗透压力增大而减小。同时，与2 MPa渗压相比，4,6,7 MPa渗压下最大变形模量依次降低了1，0.85，0.75GPa，最大变形模量对应的轴向应变随渗压的增大有明显后移趋势。

[1]蔡美峰，何满潮，刘东燕. 岩石力学与工程[M]. 北京：科学出版社，2002：112-119.

[2]杨天鸿. 岩石破裂过程的渗流特性:理论、模型与应用[M]. 北京.科学出版社, 2004.

[3]张广超, 何富连. 深井高应力软岩巷道围岩变形破坏机制及控制[J]. 采矿与安全工程学报, 2015, 32(4): 571-577.

ZHANG Guangchao, HE Fulian. Deformation failure mechanism of high stress deep soft roadway and its control[J]. Journal of Mining & Safety Engineering, 2015, 32(4):571-577.

[4]梁光川, 李庆, 彭星煜,等. 埋藏深度对盐岩储气库溶腔变形的影响研究[J]. 中国安全生产科学技术, 2016, 12(10):74-80.

LIANG Guangchuan, LI Qing, PENG Xingyu, et al. Research on influence of buried depth to cavity deformation of salt rock gas storage[J]. Journal of Safety Science and Technology, 2016, 12(10):74-80.

[5]贾宏俊, 王辉. 软岩大变形巷道刚柔结合支护方法研究[J]. 中国安全生产科学技术, 2015, 11 (10):11-16.

JIA Hongjun，WANG Hui. Research on rigid-flexible combined support method of soft rock roadway with large deformation[J].Journal of Safety Science and Technology,2015, 11 (10):11-16.

[6]马海涛, 刘宁武, 王云海,等. 金属矿山采空区灾害防治技术研究综述[J]. 中国安全生产科学技术, 2014(10):75-80.

MA Haitao, LIU Ningwu, WANG Yunhai, et al. Review on research status of controlling techniques for goaf disaster in metal mine[J]. Journal of Safety Science and Technology, 2014(10):75-80.

[7]刘俊新, 张可, 刘伟,等. 不同围压及应变速率下页岩变形及破损特性试验研究[J]. 岩土力学, 2017(S1): 43-52.

LIU Junxin, ZHANG Ke ,LIU Wei, et al. Experimental study of mechanical behaviours of shale under different confining pressures and different strain rates[J]. Rock and Soil Mechanics, 2017 (S1):43-52.

[8]BIENIAWSKI Z T. Time-dependent behavior of fractured rock[J]. Rock Mech. & Rock Eng., 1970, 2(3): 123-137.

[9]PENG S S, PODNIEKS E R. Relaxation and the behavior of failed rock[J]. Int. J. Rock Mech. Min. Sci. &Geomech. Abst., 1972, 9(6): 699-712.

[10]PENG S S. Time-dependent aspects of rock behavior as measured by a servocontrolled hydraulic testing machine [J]. Int. J. Rock Mech. Min. Sci. & Geomech. Abst., 1973, 10(3): 235-246.

[11]马林建, 刘新宇, 许宏发,等. 循环荷载作用下盐岩三轴变形和强度特性试验研究[J]. 岩石力学与工程学报, 2013, 32(4):849-856.

MA Linjian, LIU Xinyu, XU Hongfa, et al. Deformation and strength properties of rock salt subjected to triaxial compression with cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4):849-856.

[12]FUENKAJORN K，PHUEAKPHUM D. Effects of cyclic loading on mechanical properties of Maha Sarak ham salt[J]. Engineering Geology，2010，112(1)：43-52.

[13]杨春和, 马洪岭, 刘建锋. 循环加、卸载下盐岩变形特性试验研究[J]. 岩土力学, 2009, 30(12):3562- 3568.

YANG Chunhe, MA Hongling, LIU Jianfeng. Study of deformation of rock salt under cycling loading and unloading [J]. Rock and Soil Mechanics, 2009, 30(12): 3562- 3568.

[14]苏承东, 张振华. 大理岩三轴压缩的塑性变形与能量特征分析[J]. 岩石力学与工程学报, 2008, 27(2): 273-280.

SU Chengdong, ZHANG Zhenhua. Analysis of plastic deformation and energy property of marble under pseudo-triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 273-280.

[15]杨圣奇，徐卫亚，苏承东. 大理岩三轴压缩变形破坏与能量特征研究[J]. 工程力学，2007，24(1)：136-141.

YANG Shengqi, XU Weiya, SU Chengdong. Study on the deformation failure and energy properties of marble specimen under triaxial compression[J]. Engineering mechanics, 2007，24(1)：136-141.

[16]李文璞. 采动影响下煤岩力学特性及瓦斯运移规律研究[D]. 重庆：重庆大学, 2014.