FPS异常的2种不同解释方法对比

肖波，刘海飞，戴前伟



FPS异常的2种不同解释方法对比

肖波1，刘海飞2，戴前伟2

(1.中国能源建设集团 广东省电力设计研究院，广东 广州，510600；2.中南大学 地球科学与信息物理学院，湖南 长沙，410083)

从有限单元法正演模拟入手，采用最小二乘法进行反演计算，通过VC++程序实现，对多个地电模型实例进行计算，并将最小二乘法反演结果与圆弧交汇−相对强度计算结果进行对比。研究结果表明：圆弧交汇−相对强度法对简单模型适用性高，由其反演成果所确定异常体中心位置甚至会优于最小二乘法最优化反演结果；最小二乘法能适应各种地电条件对多种模型进行反演计算，其计算结果优于圆弧交汇−相对强度法计算结果。

电阻率；极化率；数值模拟；有限元法；反演；定量解释

固定点源激电测深法(FPS)又称固定点源双边三极测深法。该方法装置在实际工作中采用多台接受机同时测量，测量电极极距根据实际情况可灵活变化，导体极化场位置随着供电点位置不同而变化，具有较高工作效率的同时可更好地确定异常体的位置。但该装置在数据处理过程中，常规的相对强度−圆弧交汇解释方法受场源的分布位置影响大，其解释成果对模型形状、埋深半径比的依赖性较大；该方法对于单个模型的处理解释通常能取得较好效果，但对组合模型的解释通常会产生明显的假异常，从而掩盖了真实异常体的信息，为勘探解释工作带来了极大的困难。在此，本文作者从有限元正演模拟和最小二乘反演方法的角度入手，对多个地电模型进行实例计算，并将最小二乘反演结果与圆弧交汇−相对强度计算结果进行对比。

1 正演模拟

采用有限单元法进行正演模拟，将整个计算空间区域离散成许多相互连接的单元网格，通过对单元网格节点的电位进行求解得到计算域的电位分布，然后将电位分布值转化为视电阻率，再通过“等效电阻率”求取视极化率。

在二维地电条件下，点电流源场各节点电位的计算可归结为对若干个给定波数求解电位的傅里叶变换(，，)所满足的二维偏微分方程的边值问题：

式中：为电导率；和1为地面边界；∞为其他边界；I为第个供电电极的电流；为场源到测点的距离；边界处法线向量；和分别为零阶和一阶修正贝塞尔函数[1−2]。

与方程式(1)等价的变分问题为

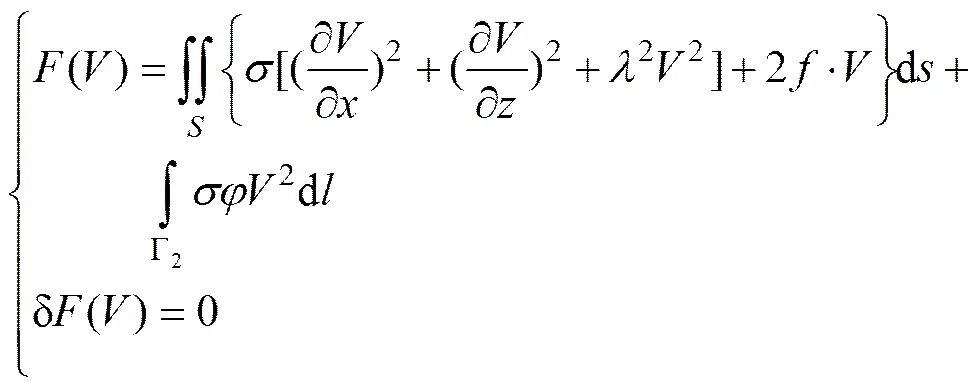
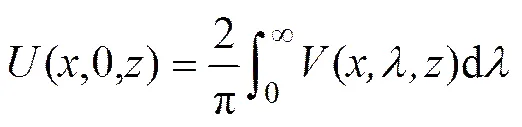
通过有限单元法数值模拟可得地表任意一点的电位，从而得到相应的视电阻率[3]：

其中：为装置系数；为供电电流；Δ为两节点之间的电势差。

当地下介质有极化特性时，其等效电阻率为

式中：为介质电阻率；为介质极化率。利用上面所述的电阻率二维正演方法对等效电阻率进行正演，可以得到等效视电阻率：

由式(5)可得到视极化率η为

2 解释方法

2.1 常规定量解释方法

电法勘探中，有2个或者2个以上的供电点，分别以供电点到视电阻率s曲线、视极化率s曲线极值点的距离为半径画圆弧，根据圆弧的交点确定异常体的中心位置，称为圆弧交汇法[3−4]，如图1所示。

图1 圆弧交汇法示意图

相对强度法是将二维地电断面网格化，以各网格节点到点源的距离为半径作圆弧，取圆弧与水平地表交点位置对应的视电阻率、视极化率为该网格节点的值，位于点源坐标左边的网格节点由视电阻率、视极化率左支实测值确定，位于点源坐标右边的网格节点由视电阻率、视极化率右支实测值确定。对于多个点源，先对各节点上求和，进而计算出他们的平均值找出断面上最大的平均值，用各网格节点的平均值去除以，最后得到了相对强度；对于低阻体，提取断面上最小平均值，然后用除以各网格节点的平均值，从而突出断面异常体的中心位置。相对强度法的作图示意图如图2所示。

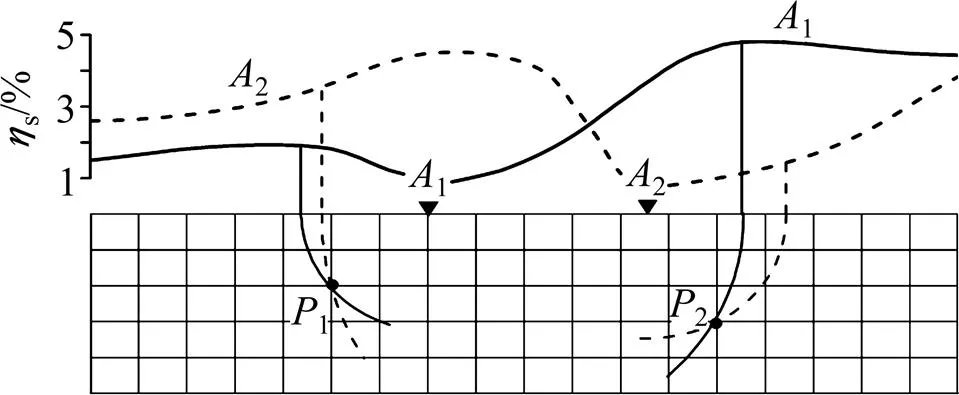
图2 相对强度法的成图示意图

2.2 最小二乘反演法

采用基于圆滑约束最小二乘反演方法，利用正演模型和实测数据构造一目标函数，并使其达到极小。圆滑约束最小二乘法是基于以下方程[5−8]：

对方程组(7)进行求解，得到模型参数修正矢量Δ，将其代入式(8)便得到新的预测模型参数矢量(k)：

如此重复，直至模拟数据和实测数据之间的平均均方误差满足要求为止[9−14]。平均均方误差为

在反演过程中，为提高求解大型、病态线性方程组的计算速度和反演效率，采用广义共轭梯度算法(GCG)[15−16]对偏导数矩阵进行求解，其基本公式为

其实现步骤如下。

1) 初始向量(0)=0，(0)=，(0)=T(0)=(0)；误差限，阻尼因子；

如果||(0)||≤，则终止，否则转入步骤3)；对于=2，3，…，max，计算到步骤10)；

8) 如果||(j+1)||≤终止, 否则转入步骤9) ；

3 模型计算

采用有限单元法数值计算进行正演模拟，分别用圆弧交汇−相对强度法成图反演和最小二乘最优化反演进行反演计算。对多个模型实例的计算结果进行对比分析。

综合考虑数据量、反演效果及工作量之间的关系，拟设7个测深供电点：1=40 m，2=60 m，3=80 m，4=100 m，5=120 m，6=140 m，7=160 m。为达到有效勘探深度，勘探区域为−50~250 m，取0~200 m进行剖面成图，反演结果剖面图中方框内为模型投影图。

3.1 正方柱体模型Ⅰ

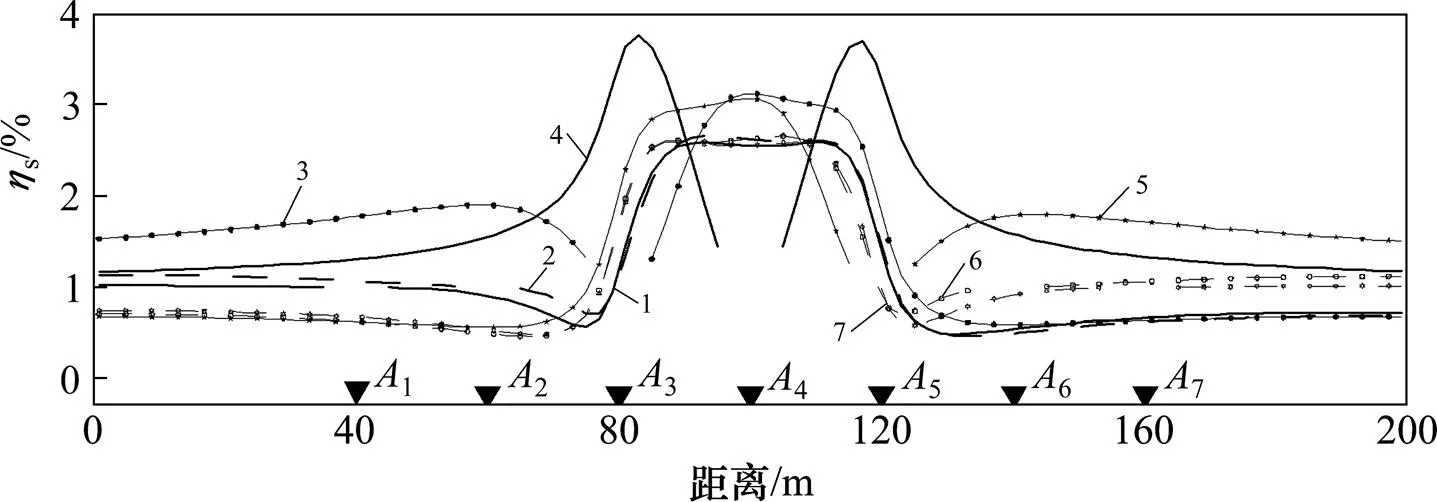
模型Ⅰ为长×宽为20 m×20 m低阻、高极化正方柱体(见图3)，中心位置为(100 m，−20 m)，电阻率为1=50 Ω∙m，极化率为1=5.0%；背景电阻率为0=100 Ω∙m，极化率为0=1.0%。正演模拟各点源对应的视极化率曲线如图4所示。视极化率相对强度如图5所示。视极化率最小二乘反演结果如图6所示。

图3 正方柱体模型示意图

1—A1；2—A2；3—A3；4—A4；5—A5；6—A6；7—A7

图5 正方柱体模型视极化率相对强度

图6 正方柱体模型视极化率最小二乘反演结果

对比图5和6可知：最小二乘反演、圆弧交汇−相对强度法能通过视极化率反演成图能较好的体现出正方柱体的位置。视极化率相对强度法计算结果能较准确地反映出正方柱体的中心埋深位置；而最小二乘反演结果未能体现模型极化体中心，反演极化体中心位于实际模型中上部，但异常体处于模型投影范围内。

3.2 正方柱体模型Ⅱ

模型Ⅱ为长×宽为20 m×20 m正方低阻、高极化柱状体(见图7)，中心位置为(40 m，−17 m)，电阻率为1=50 Ω∙m，极化率为1=5.0%；背景电阻率为0=100 Ω∙m，极化率为0=1.0%。正演模拟各点源对应的视极化率曲线如图8所示。视极化率相对强度如图9所示。视极化率最小二乘反演结果如图10所示。

图7 正方柱体模型示意图

1—A1；2—A2；3—A3；4—A4；5—A5；6—A6；7—A7

图9 正方柱体模型正演视极化率相对强度图

图10 正方柱体模型视极化率最小二乘反演结果

由图9可知：视极化率的相对强度中心与模型实际位置中心较吻合，但相对强度等值线不能确定模型的基本形态。相对强度中心周边等值线向右成圆弧形倾斜，其原因是采用圆弧交汇法，与点源距离相等的各网格节点视电阻率、视极化率的取值相同，当点源分布相对模型中心不对称时，各网格节点视电阻率、视极化率难以均衡，从而导致相对强度中心周边等值线呈圆弧形发生明显倾斜。

图10表明：最小二乘反演能基本反映了模型的形态和位置；反演结果异常体顶面与实际模型顶面较吻合。但异常体中心位于实际模型中的中上部，模型的底界面无法通过异常体形态确定。图10还表明：最小二乘反演结果受点源位置分布影响小。

3.3 水平板状体模型

模型为长×宽为40 m×40 m水平低阻、高极化板状体(见图11)，中心位置为(100 m，−10 m)，电阻率1=50 Ω∙m，极化率1=5.0%；背景电阻率0=100 Ω∙m，极化率0=1.0%。正演模拟各点源对应的视极化率曲线如图12所示。视极化率相对强度如图13所示。视极化率最小二乘反演结果如图14所示。

图11 水平板状体模型示意图

1—A1；2—A2；3—A3；4—A4；5—A5；6—A6；7—A7

图13 水平板状体模型正演视极化率相对强度

图14 水平板状体模型视极化率最小二乘反演结果

对比图13和图14可知：最小二乘反演能很好的反映出水平低阻、极化板状体的埋深、基本形态，异常体位置与模型实际位置对应关系较好；圆弧交汇−相对强度法能基本确定水平低阻、高极化板状体位置，但视极化率相对强度中心位于低阻极化体模型位置正下部边缘处，从视极化率相对强度等值线图无法确定模型的基本形态。

3.4 组合模型

模型为2个长×宽为20 m×20 m正方柱形低阻、高极化模型(见图15)，中心位置分别为(80 m，−18 m)、(120 m，−18 m)，电阻率1=50 Ω∙m，极化率1=5.0%；背景电阻率0=100 Ω∙m，极化率0=1.0%。正演模拟各点源对应的视极化率曲线如图16所示，视极化率相对强度如图17所示，视极化率最小二乘反演结果如图18所示。

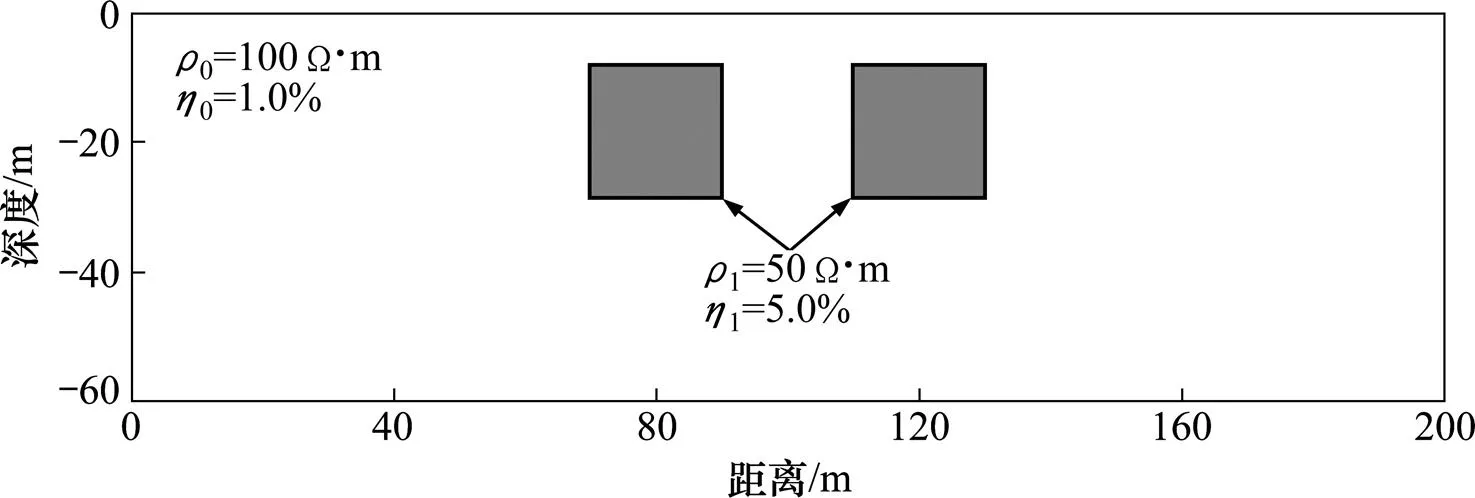
图15 组合模型示意图

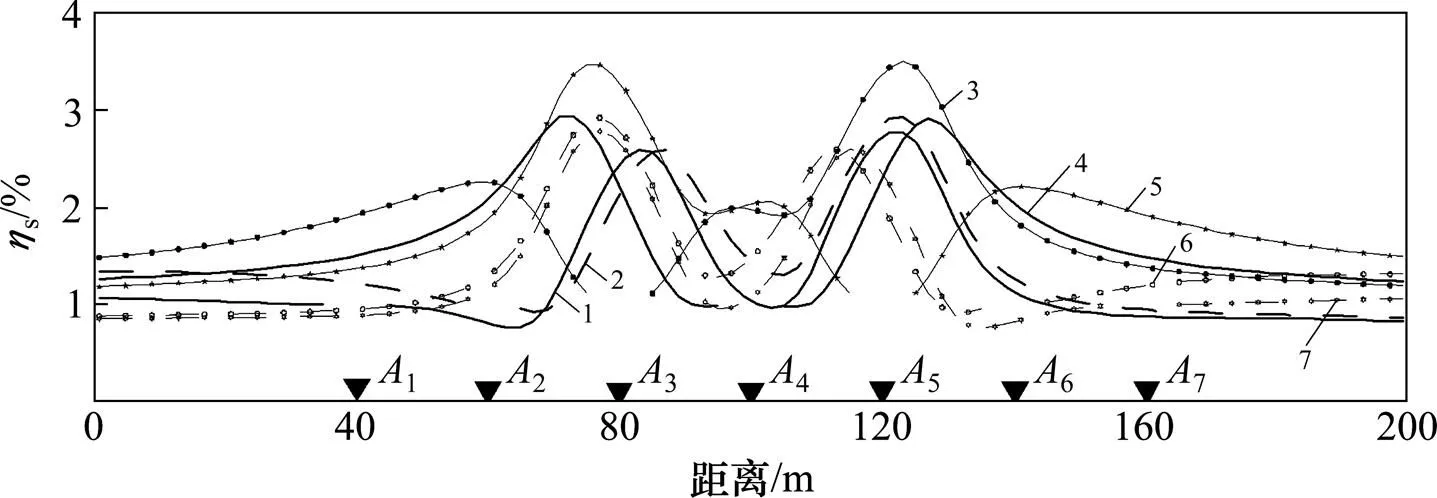
1—A1；2—A2；3—A3；4—A4；5—A5；6—A6；7—A7

图17 组合模型正演视极化率相对强度

图18 组合模型视极化率最小二乘反演结果

图17表明：组合模型视极化率相对强度中心与模型的实际位置中心相吻合；但模型的中垂线下方位置存在1个明显的假异常，其原因是圆弧交汇法和相对强度法是建立在单个模型之上。对于组合模型，由于同一点源计算的视极化率曲线会产生2个极值点，从而进行圆弧交汇时就会产生其他相对强度，即为假异常，假异常通常随着模型间的距离增大而变深。

图18表明：最小二乘视极化率反演较好地反映了组合模型的实际位置，反演结果与实际模型较吻合，无明显假异常存在，但反演结果难以反映出模型的底界面。

后期对高阻、高极化模型进行模型计算对比，其对比结论与低阻、高极化模型计算对比结果一致：最小二乘法反演结果优于圆弧交汇−相对强度法。

4 结论

1) 固定点源激电测深具有简单、高效的特点，其解释方法圆弧交汇−相对强度法与最小二乘反演都能较准确地反映出异常体中心位置，这2种解释方法直观且其解释结果与实际结果较符合。

2) 圆弧交汇−相对强度法对于单个模型能准确地反映出模型的中心埋深位置；但该解释方法受场源位置影响大；对于稍复杂模型未能精确的体现出异常体的位置及形状，对于组合模型通常会产生较明显的假异常。

3) 最小二乘反演不受场源位置影响，能较好地反映出复杂模型的实际位置及轮廓，在对组合模型进行反演解释时候，不会产生假异常；但该解释方法难以体现模型的下底面位置。

[1] 李小康. 时间域激电二维正演研究[D]. 北京: 中国地质大学地球物理与信息技术学院, 2008: 27−47.
LI Xiaokang. 2D forward numerical simulation of ip method in time domain[D]. Beijing: China University of Geosciences. School of Geophysics and Geoinformation Systems, 2008: 27−47.

[2] 戴前伟, 肖波, 冯德山, 等. 基于二维高密度电阻率勘探数据的三维反演及应用[J]. 中南大学学报(自然科学版), 2012, 43(1): 293−310.
DAI Qianwei, XIAO Bo, FENG Deshan, et al. 3-D inversion of the high density resistivity method based on 2-D exploration data and its application[J]. Journal of Central South University (Science and Technology), 2012, 43(1): 293−310.

[3] 刘国兴. 电法勘探原理与方法[M]. 北京: 地质出版社, 2005: 111−128.
LIU Guoxing, Electrical prospecting principle and method[M]. Beijing: Geological Publishing House, 2005: 111−128.

[4] 李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005: 258−260.
LI Jinming. Electric field and electrical prospecting[M]. Beijing: Geological Publishing House, 2005: 258−260.

[5] 李金铭, 魏文博, 陈本池, 等. 固定点源测深法定量解释研究[J]. 物探与化探, 1997, 21(3): 187−196.
LI Jinming, WEI Wenbo, CHEN Benchi, et al. The quantitative interpretation of the fixed point source sounding methods[J]. Geophysical & Geochemical Exploration, 1997, 21(3): 187−196.

[6] 陈本池, 李金铭, 魏文博. 起伏地形条件下固定点源测深法定量解释研究[J]. 现代地质, 1998, 12(1): 123−129.
CHEN Benchi, LI Jinming, WEI Wenbo. A study of quantitative interpretation for fixed point source sounding method under undulatory terrai[J]. Geoscience, 1998, 12(1): 123−129.

[7] 强建科, 阮百尧. 用FPS定量解释法实现三维近似成像的探讨[J]. CT理论与应用研究, 2003, 12(1): 13−16.
QIANG Jianke, RUAN Bairao. The study of 3-D IP anomaly by fixed point source sounding[J]. Study on the theory and Application of CT, 2003, 12(1): 13−16.

[8] 强建科, 罗延钟, 熊彬. 固定点源测深激电异常研究[J]. 地球物理学进展, 2005, 20(4): 1176−1183.
QIANG Jianke, LUO Yanzhong, XIONG Bin. Study on the abnormal fixed point source sounding IP[J]. Progress in Geophysics, 2005, 20(4): 1176−1183.

[9] 熊彬, 阮百尧, 黄俊革. 直流电阻率测深中二维反演程序对三维数据的近似解释[J]. 地球科学(中国地质大学学报), 2003, 28(1): 102−106.
XIONG Bin, RUAN Baiyao, HUANG Junge. Approximate interpretation of 3-D data using 2-D inversion program in the DC resistivity sounding[J]. Earth Science (Journal of China University of Geosciences), 2003, 28(1): 102−106.

[10] 黄俊革, 阮百尧. 直流电阻率测深中二维与三维反演结果的对比与分析[J]. 物探与化探, 2004, 28(5): 447−450.
HUANG Junge, RUAN Baiyao. An analytical comparison between 2D and 3D inversions in dc resistivity sounding[J]. Geophysical & Geochemical Explopation, 2004, 28(5): 447−450.

[11] 黄俊革, 王家林, 阮百尧. 三维高密度电阻率E-SCAN法有限元模拟异常特征研究[J]. 地球物理学报, 2006, 49(4): 1206−1214.
HUANG Junge, WANG Jialin, RUAN Baiyao. A study on FEM modeling of anomalies of 3-D high-density E-SCAN resistivity survey[J]. Chinese Journal of Geophysics, 2006, 49(4): 1206−1214.

[12] 刘海飞. 高密度数据处理方法研究[D]. 长沙: 中南大学信息物理工程学院, 2003: 30−60.
LIU Haifei. The processing method of High-density data[D]. Changsha: Central South University. School of Info-physics and Geomatics Engineering, 2003: 30−60.

[13] 黄俊革. 三维电阻率/极化率有限元正演模拟与反演成像[D]. 长沙: 中南大学信息物理工程学院, 2003: 20−60.
HUANG Junge. 3-Dresistivity/IP modeling and inversion based on FEM[D]. Changsha: Central South University. School of Info-physics and Geomatics Engineering, 2003: 20−60.

[14] 张大海, 王兴泰. 二维视电阻率断面的快速最小二乘反演[J]. 物探化探计算技术, 1999, 21(1): 1−12.
ZHANG Dahai, WANG Xingtai. Rapd least-squares inversion of 2-D apparent resistivity pseudosection[J]. Computing Techniques for Geophysical And Geochemical Exploration, 1999, 21(1): 1−12.

[15] 吴小平, 徐果明. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 2000, 43(3): 420−427.
WU Xiaoping, XU Guoming. Study 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics, 2000, 43(3): 420−427.

[16] 周竹生. 广义共轭梯度算法[J]. 物探与化探, 1996, 20(5): 351−358.
ZHOU Zhusheng. The generalized conjugate gradient algorithm[J]. Geophysical and Geochemical Exploration, 1996, 20(5): 351−358.

Two different interpretation methods about FPS anomaly

XIAO Bo1, LIU Haifei2, DAI Qianwei2

(1. Guangdong Electric Power Design Institute, China Energy Engineering Group, Guangzhou 510600, China;2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

The plurality of geoelectric model instance was calculated based on the forward modeling of the finite element method, using the least square method and the program with VC++. Then the least square inversion results and arc intersection−relative intensity calculation results were compared. The results show that arc intersection−relative intensity method has high applicability in simple model, the inverse mapping effect is even superior to the least square optimization inversion results in determining the center of abnormal body position. The least square inversion method can adapt various geoelectric conditions on a variety of complex model inversion, and the inversion effects of the complex model and combined model are superior to the calculation results of the arc intersection−relative intensity method.

resistivity; polarizability; numerical simulation; finite element method; inversion; quantitative interpretation

P631

A

1672−7207(2015)02−0595−08

2014−02−13；

2014−04−20

国家自然科学基金资助项目(41374118，41174102，41074085)；教育部博士点基金资助项目(20120162110015)(Project (41374118, 41174102, 41074085) supported by the National Natural Science Foundation of China; Project (20120162110015) supported by the Doctoral Fund of Ministry of Education of China)

戴前伟，博士，教授，从事电磁法方法及理论、工程地球物理勘探等研究；E-mail：qwdai@mail.csu.edu.cn

10.11817/j.issn.1672-7207.2015.02.030

(编辑 赵俊)