有效思维课堂在数学学科中的应用

隋 欣



有效思维课堂在数学学科中的应用

隋 欣

（延边第二中学，吉林 延吉 133000）

有效思维课堂是一种的教学设计理念，在这种理念的指导下，能够在有限的课堂中使学生达到最大的学习效果，充分深化学生的思维，提高课堂的效率。本文以一节概念课为例阐述了有效思维课堂在数学学科教学的应用。

高中数学教学；有效思维课堂；应用

在高中数学教学中，数学概念知识的重要组成部分，更是研究性质的基础。因此，在概念课的授课中，更注重的是知识的产生，定义的探究成为主要内容。以概念内容为基础，将训练思维的过程贯穿于各个教学环节中，从进而促进思维能力的发展。

下面以一节概念课抛物线及其标准方程为例，教学设计过程以学生带着问题为主线，不断探究发现，体现学思结合。学生在此过程中，体验数学发现、运用、创造的过程。

一、问题——激发思维

教学设计的第一步就是概念如何引入，教师如果能巧妙设计新课引入不仅能够降低学生学习新知识的难度，促进学生对概念的接受、理解，而且能使学生的学习主动性能调动起来，整一节课，学生就会有一个成功的开始，在成功的体验中完成新知识点的学习。

本节通过初中学习凹面镜的知识，提出问题：已知凹面镜的口径（直径）为4m，深度为1m，火炬应放在何处点燃最佳？学生只知道结论，但从数量关系上还无从知晓，本节在已学知识的基础上抛出问题，激发学生思维。从生活中的具体事物，先从感性认知开始。通过展示生活中的抛物线图片，激发学生的学习兴趣，进而能够主动地参与学习。

二、发散——深化思维

概念的发现与理解是概念教学的重点内容，学生经过分析、比较、概括获得的理性上的概念。通过课前课件的引入，学生主动探索，激发学生的思维，进而更好的去理解概念。抽象的概念要通过动手操作、观察得出的结果更易于接受、理解。教师在概念课的教学设计中应针对高中学生的心理特点，创造机会让学生去探索。

探究1、抛物线的定义

本节笔者设计三角板实验（如右图），学生通过“画、思、研” 等学习活动。通过“画”积极调动学生直观感受抛物线是怎样得到的；通过“思”，观察图象发现抛物线上的点到定点与定直线的距离；通过“议”，得出定点不在定直线上，从而得出完整抛物线的定义。

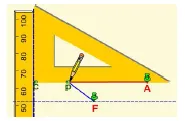
探究2、抛物线的标准方程

方程的得出要多次地进行，标准方程的形成也不是一步就能得出来的，经过多次列举、归纳，在此过程发生学生的思维，让学生真正理解概念。

本节通过学生自主建系，得出三种不同的方程比较过程得出标准方程的概念。

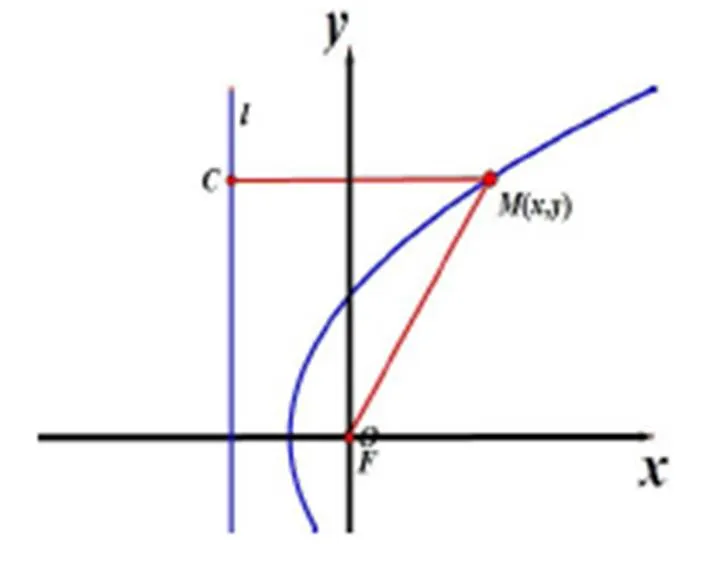
y2=2px-p2

y2=2px-(p>0)

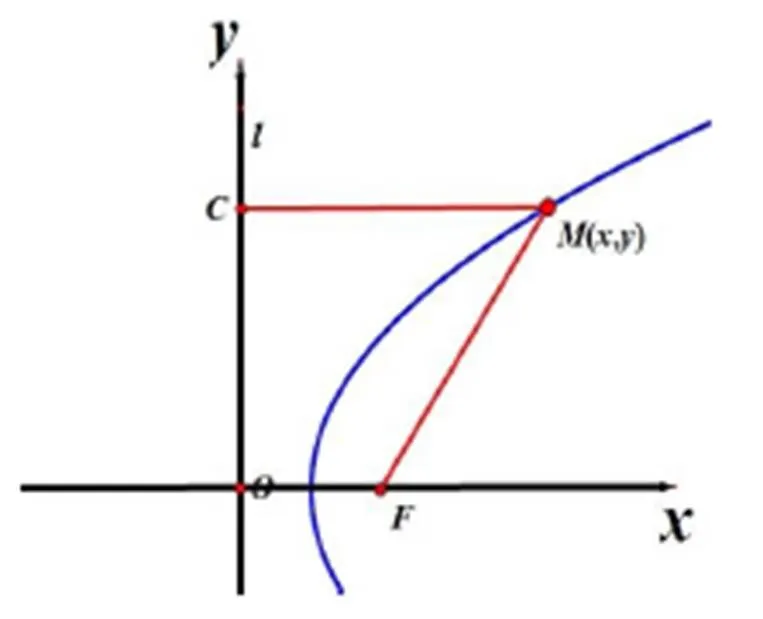
y2=2px+p2

探究3、四种抛物线的标准方程

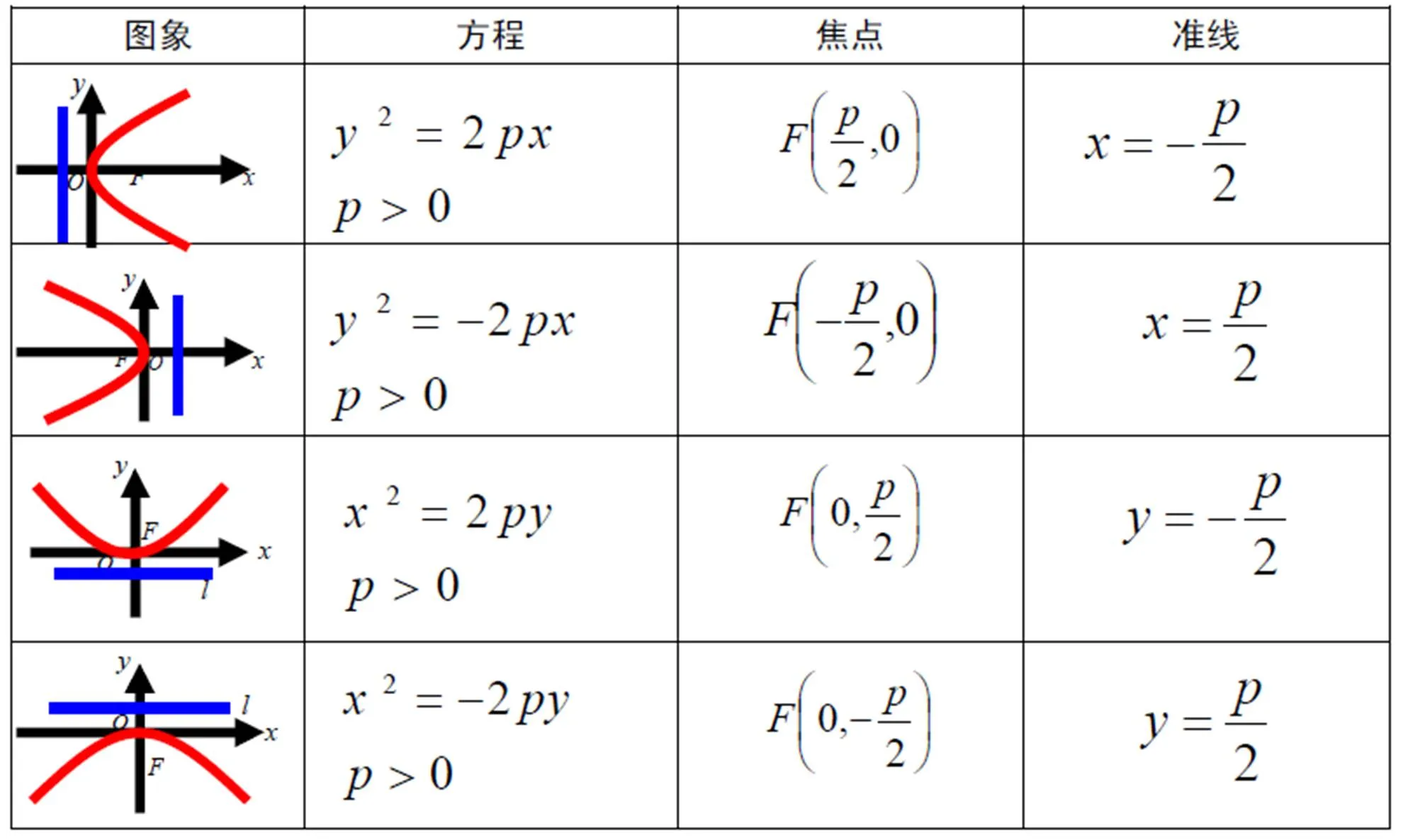
学生通过类比图象及方程特点，总结适合自己记忆的方法。

三、收敛——强化思维

收敛过程是课堂的中心，通过此过程可以让学生发散的思维得到综合。在得出概念的过程中，学生通过探究，思维得到锻炼，但要张弛有度，学生的方法多样，可能会出现错误的思维过程，因此需要教师及时指导，不断强化学生的思维过程。在此过程中，引导学生选择简单，快捷的思维方式进而对所学内容加深整理。

本节在得出开口向右抛物线的标准方程，通过图形变换，如下：

结合以上图象的变化过程，不必再重复推导标准方程的过程，更锻炼了学生的思维，加深了对方程的记忆过程。

四、拓展思维

得出概念，明确方程，但并不等于真实理解，此时须有一个消化吸收的过程。通过变式训练促使知识在思维过程中再次飞跃，达到一定高度。本节通过例题、变式训练加深对定义及标准方程的记忆，同时总结出抛物线标准方程的方法：先定位，后定量。在此基础上解决课前导入的问题，起到首尾呼应的作用。

五、训练思维

在概念的熟练运用中，加强对知识之间的联系，形成系统，发展学生的能力。本节在学生已经得出的方法的基础上，进行编制求抛物线标准方程的题，形成系统思维、发展概念。

在现代课堂教学中，应有机地运用各种教学方法和手段，全面达成“三维目标”，变学会为会学。 在掌握知识的基础上，思维得到充分的发展，为良好的学习习惯做好铺垫，进而达到事半功倍的效果。思维型课堂的教学，有效的促进师生互动，结合人机互动，激发课堂的思维活动，还给学生一个真实的课堂，真正提高课堂教学的效率。

[1]孙玉恒,李宁.双互动四统一教学范式探析[J]. 延边教育学院学报,2010(6).

[2]余文森.有效教.学十讲[M].上海:华东师范大学出版社,2009.

[3]王金霞.有效课堂教学的实施与策略[M].石家庄:河北人民出版社,2010.

2015—04—24

G633.6

A

1673-4564（2015）03—0124—03