关于调和数的等式*

申玲玲，郜静霞(重庆师范大学数学学院，重庆401331)

关于调和数的等式*

申玲玲，郜静霞
(重庆师范大学数学学院，重庆401331)

对Jonathon Peterson的著名的二项式等式进行推广;用局部分解的方法获得一个关于调和数的新等式，应用等式可以获得一些另外的关于调和数的二项式等式.

二项式等式;局部分解;调和数

1　预备知识

关于调和数定义:

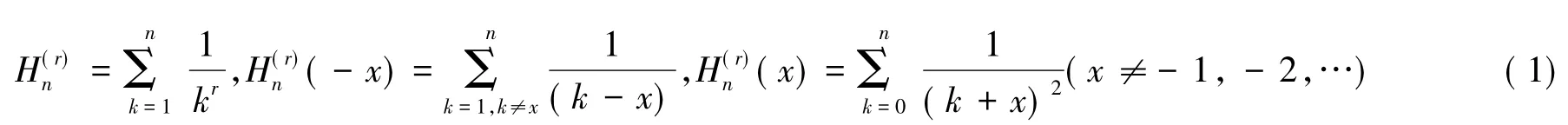
引理1若m，n，r∈N，θ∈R，r＞n－m－2，那么

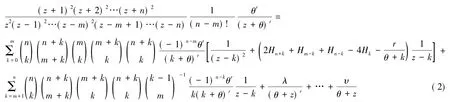
证明由局部分解可以得到

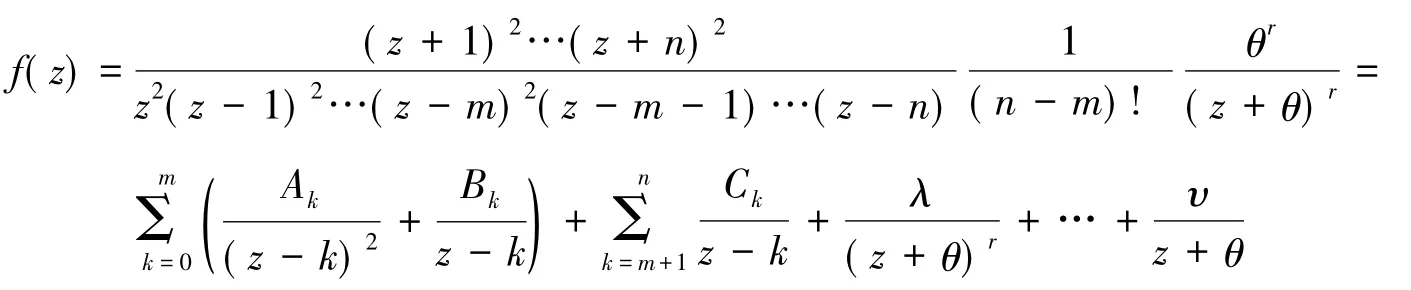
其中系数Ak，Bk和Ck待定.

当0≤k≤m时，有

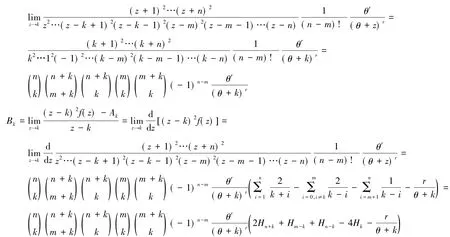
当m+1≤k≤n时，有

2　推广的新等式

Jonathon［2］给了一个简单的有趣的方法来证明二项式等式，即概率的方法，在这里将其推广并用局部分解及文献［3］中的方法证明，其中等式右边可以表示成贝尔多项式［4］的形式.

定理1若m，n，r∈N，θ∈R，r＞n－m－2，θ＞0那么当时，有

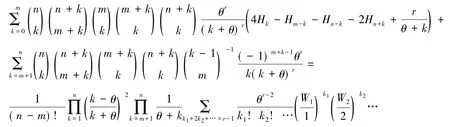
当θ∈{1，2，…，n}时，有

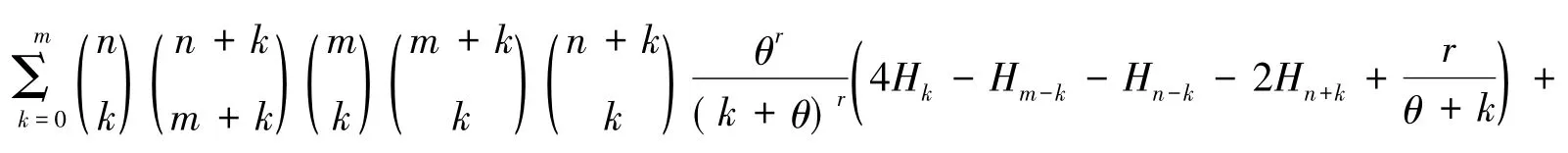
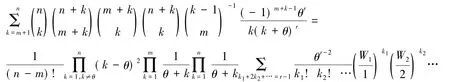
证明将引理1中式(2)两边乘以z，并使z→∞可以得到

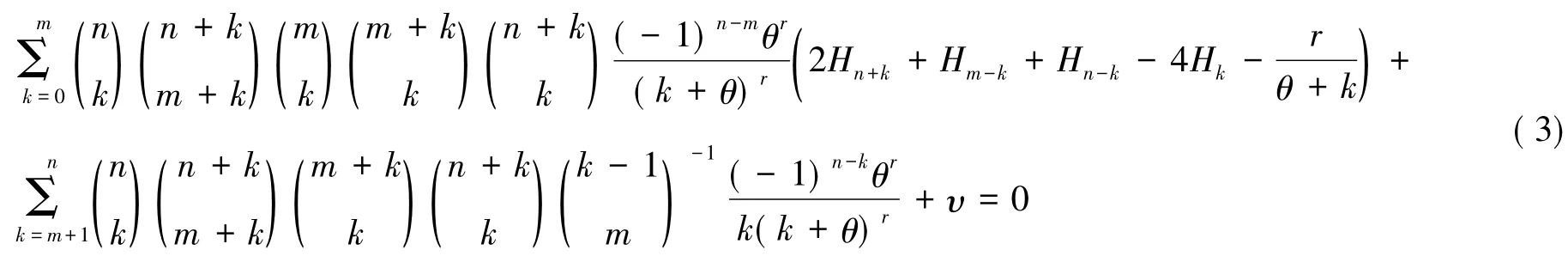
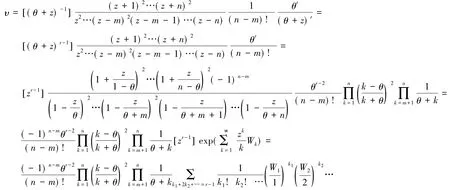
当θ∈{1，2，…，n}时，有

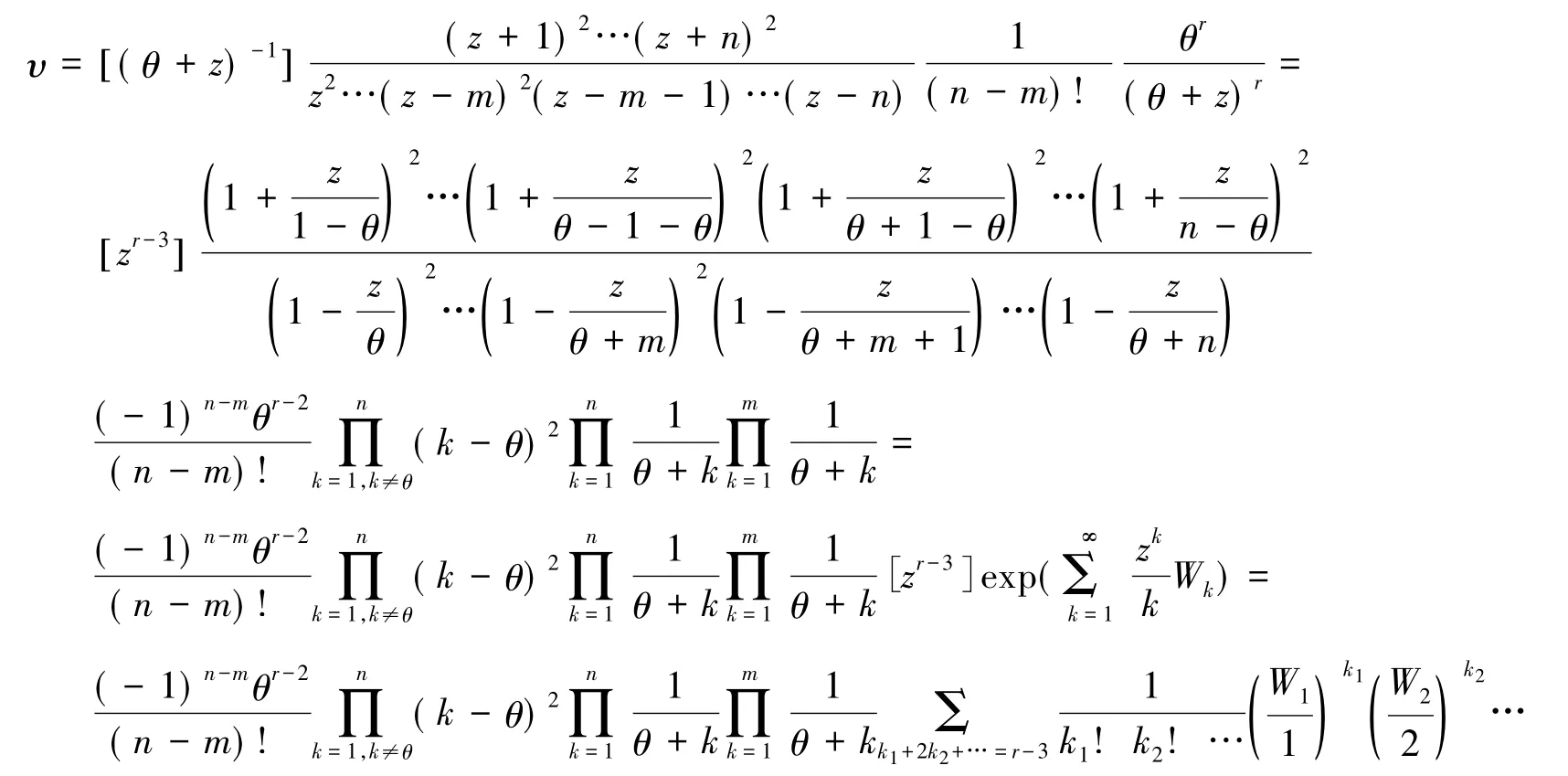
3　应用

推论1设m=0，n，r∈N，θ∈R，θ＞0和r＞n－2，当时，有

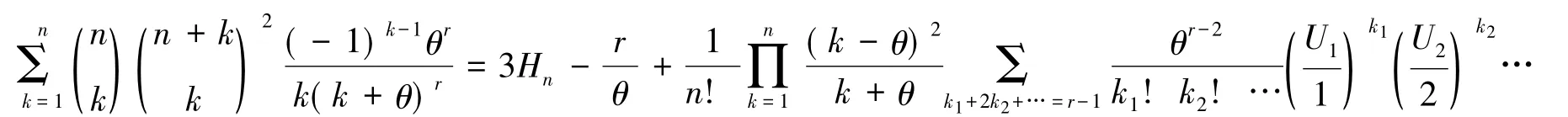
当θ∈{1，2，…，n}时，有

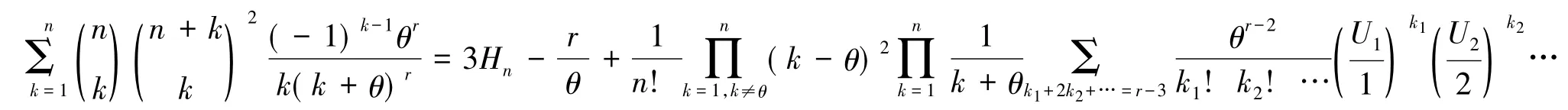
当θ∈{1，2，…，n}时，有

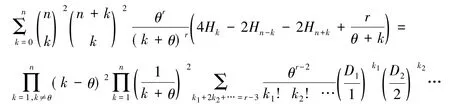
［1］CHUW CH.A Binomial Coefficient Identity Associated with Beuker’Conjecture on Apery Numbers［J］.Electron JCombin，2004 (11):44-45

［2］PETERSON J.A Probabilistic Proof of a Binomial Identity［J］.The American Mathematical Monthly，2013(6):558-562

［3］PRODINGER H.Identities Involving Harmonic Numbers that are of Interest for Physicist［J］.Util Math，2010(83):291-299

［4］COMTET L.Advanced Combinatorics［M］.France:Presses Universitaires de France，1970

An Equation Involving Harmonic Numbers

SHEN Ling-ling，GAO Jing-xia
(School ofmathematical Sciences，Chongqing Normal University，Chongqing 401331，China)

This paper mainly focuses on the extension of binomial identity by Jonathon.A new equation involving harmonic numbers is obtained by partial fraction decomposition，by which some other binomial identities involving harmonic numbers identities are obtained aswell.

binomial identities;partial fraction decomposition;harmonic numbers

O156

A

1672－058X(2015)09－0039－04

10.16055/j.issn.1672－058X.2015.0009.010

2014－12－30;

2015－02－22.

重庆市自然科学基金(CSTC2011JJA00024).

申玲玲(1989-)，女，河南安阳人，硕士研究生，从事特殊函数研究.