部分线性回归模型中改进的差分估计及SCAD
郭雪梅(重庆大学数学与统计学院,重庆401331)
部分线性回归模型中改进的差分估计及SCAD
郭雪梅
(重庆大学数学与统计学院,重庆401331)
考虑了部分线性回归模型中回归参数向量估计的问题,提出了具有更好性质的压缩差分估计,并且将SCAD惩罚函数运用到模型中得到SCAD估计,然后通过Monte Carlo模拟了压缩差分估计和SCAD估计的相关结果,并对它们之间的优劣进行了比较.
差分估计;局部线性回归模型;SCAD;压缩估计
1 模型简介
考虑半参数回归模型:
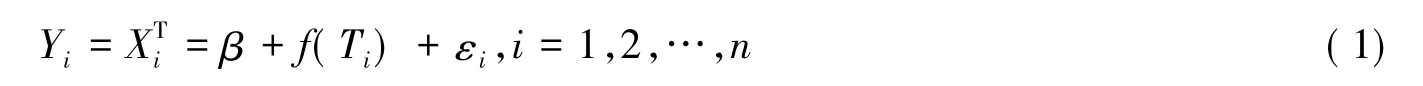
其中Yi是响应变量,受到(Xi,Ti)的影响是p维随机变量向量,Ti是一个随机变量,β=是未知的p维参数变量向量,f(·)是一个未知的平滑函数,εi是随机误差,且有
模型(1)是由Engle等提出的,主要是为了研究气候对电力需求的影响.半参数模型中参数部分带宽的选择不是一件容易的事,运用差分估计的方法是由Hall等(1990)[1]提出来的.压缩估计最初是由C.Stein[2]在1956年提出的.关于压缩估计的方法有很多,其中LAASO,SCAD等是压缩估计中标志性的方法.虽然基于差分的估计和压缩估计得到了很大的发展,但是此文是第一个在部分回归模型中运用差分来提高压缩估计值的性质,并且和SCAD惩罚估计进行比较.
2 符号及假设
为了更好地介绍差分估计,列举了一些必要的符号以及假设,如下:
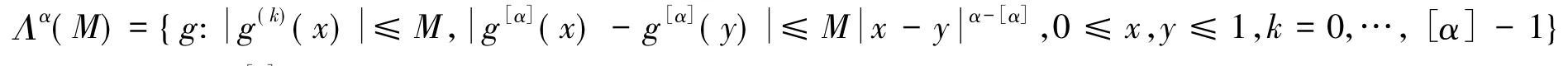
其中[α]是取整,g[α](x)表示g(x)的[α]次导.
假设1εi和(Xi,Ti)是相互独立的,对于,α>0,γ>0,有
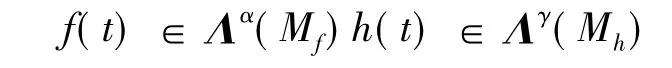
假设3 Ti的边际密度函数是Lipschitz连续的,并且不为0.
设T(1)≤T(2)≤…≤T(n)是Ti的顺序统计量,(X(1),Y(1)),…,(X(n),Y(n))是(X(i),Y(i))所对应的值,注意(X(i),Y(i))不是顺序统计量,但是(X(i),Y(i))与Ti是一致的,那么模型(1)这可以重新写成如下的形式:
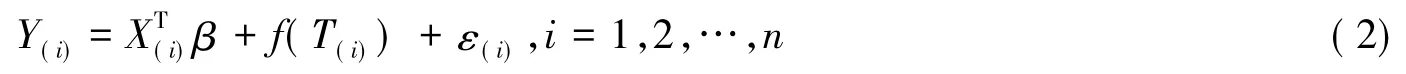

定义如下(n-m)×n维的差分矩阵:
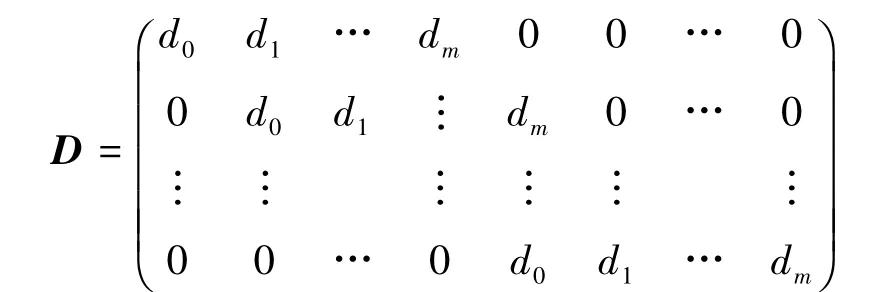
矩阵内的元素满足式(3).把这个差分序列运用到式(2)中,得到
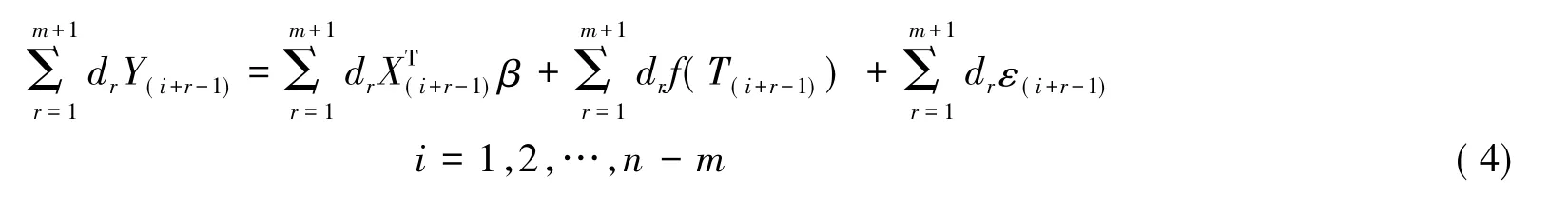
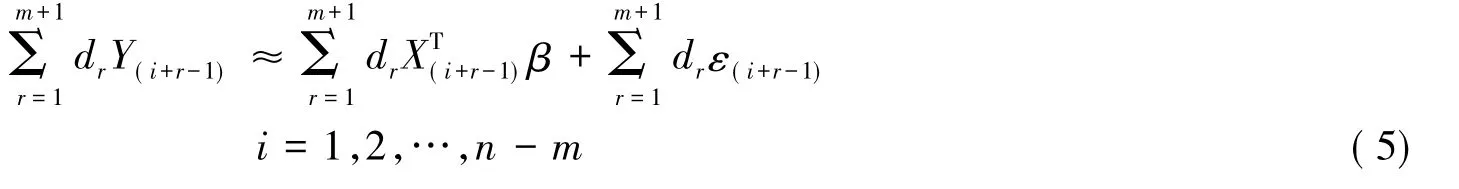
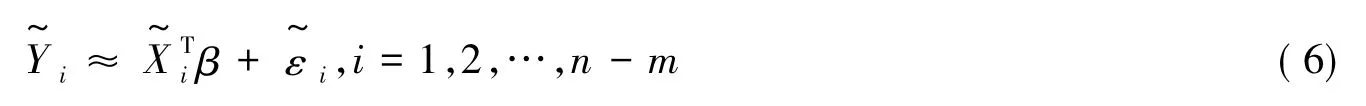
由于式(6)类似于线性模型,所以式(6)的估计值可以表示为

3 差分压缩估计的构造

假设有β的先验信息,使得Rβ=r成立,其中R是q×p的矩阵,其秩为q,r是q×1的向量,q≤p.设是β的约束差分估计,当Rβ=r成立时可以写成如下的形式:
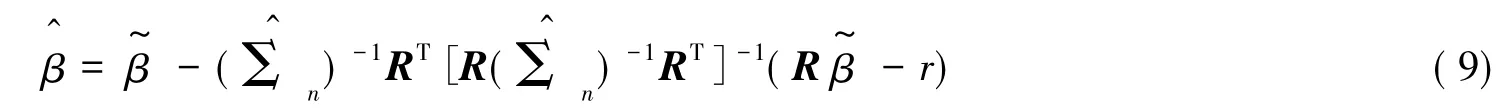
设原假设H0:Rβ=r(备择假设:H1:Rβ≠r),提出如下的检验统计量:
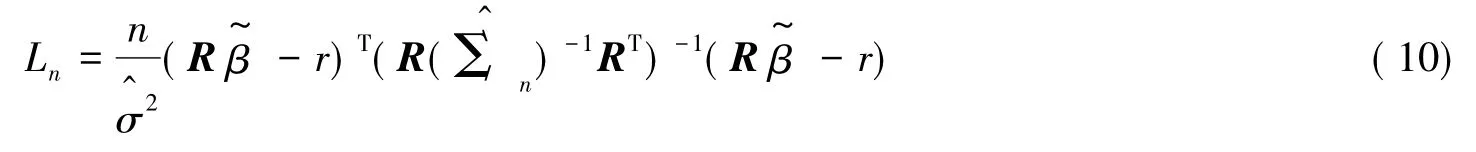
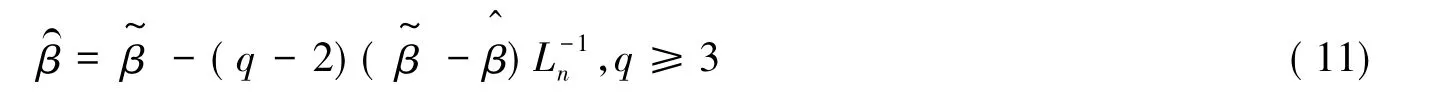
上述估计值是由无约束估计和约束差分估计的权重组成的,这个权重是原假设H0中的检验统计量的函数.但是该估计值存在一些问题,当可能会使得朝着,从而被过分地压缩,使得的符号出现一些问题.为了克服这个过度压缩的可能性,正压缩差分估计可以表示如下:
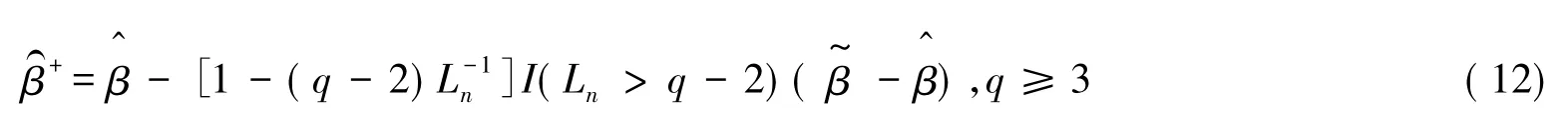
4 LASSO思想在模型(6)中的运用
给定惩罚函数pλ(.)和正则化参数λ,那么模型(6)运用变量选择方法对参数求解的过程可以表示如下:
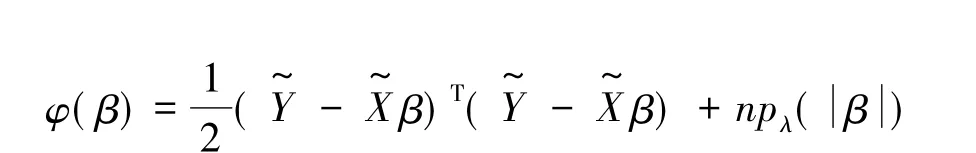
LASSO估计值可以表示为如下:
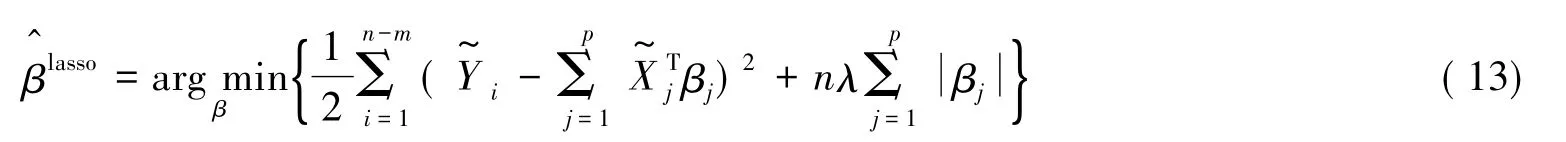
LASSO估计没有哲人性质,于是考虑SCAD估计.SCAD估计是在LASSO估计的基础上发展的.具体可以参考文献Fan和Li[6].将SCAD的惩罚函数运用到模型(6)中,可以得到SCAD估计如下:
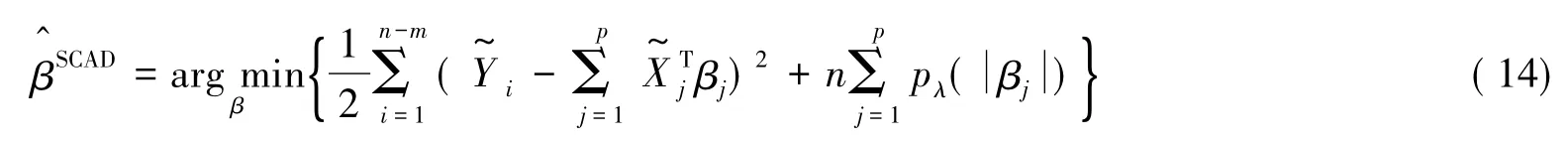
其中pλ(.)是SCAD的惩罚函数,a和λ是参数.
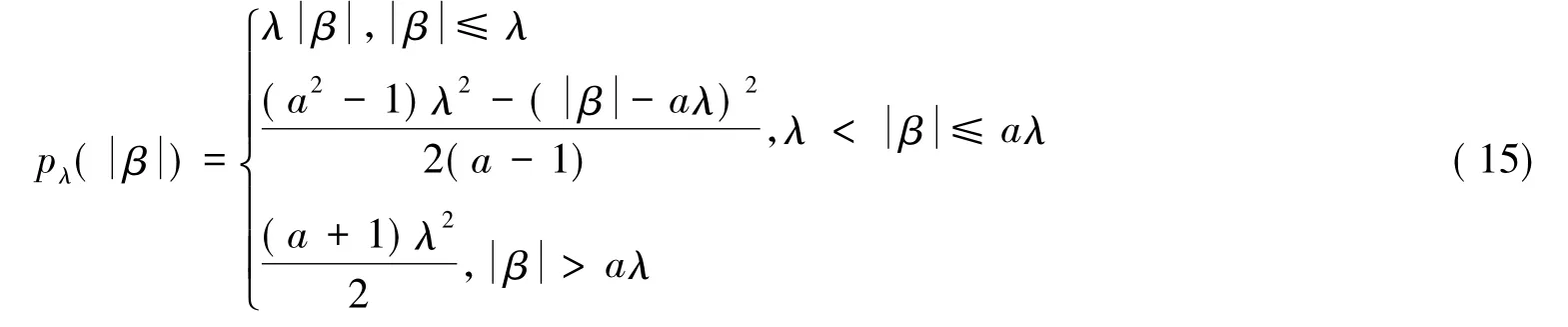
Fan和Li证明了在各种情况下,当a≡3.7时,估计值有较好的性质,在第5部分的模拟中,也选择a≡3.7,与此同时,运用GCV准则来选择正则化参数参数λ.
5 模拟
在这一部分,将通过Monte Carlo模拟来比较压缩估计和SCAD惩罚函数估计.数据都是从式(14)线性回归模型中得到的.


模拟过程中,考虑δ=0和δ≠0两种情况.在δ≠0的情况下,选择δ=0,0.2,0.4,0.6,0.8,1.0,1.2,1.4, 1.6,SCAD的正则化参数λ通过GCV准则来选择的相对有效性可以通过数值结果来表示.为了求解这些估计的相对有效性,考虑n=30,50,100,200,p1=4,p2=3,5,7,9,11.重复这样的模拟3 000次.
在不同的n和δ=0下,给出SCAD惩罚估计和压缩差分估计与的相对有效性,且(p1,p2)={(4,3),(4,5),(4,7),(4,9),(4,11)},具体的结果会在表1中展示出来.
表1 与的相对有效性(p1=4,δ=0,m=3)
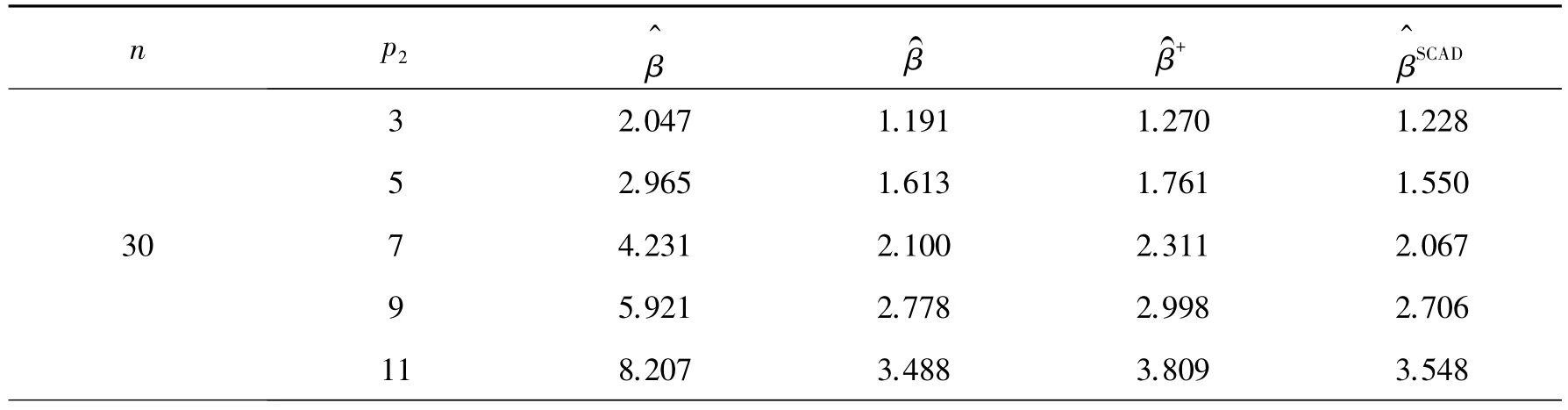
表1 与的相对有效性(p1=4,δ=0,m=3)
n p2β^β)β)+β^SCAD3 2.047 1.191 1.270 1.228 5 30 2.965 1.613 1.761 1.550 7 4.231 2.100 2.311 2.067 9 5.921 2.778 2.998 2.706 11 8.207 3.488 3.809 3.548
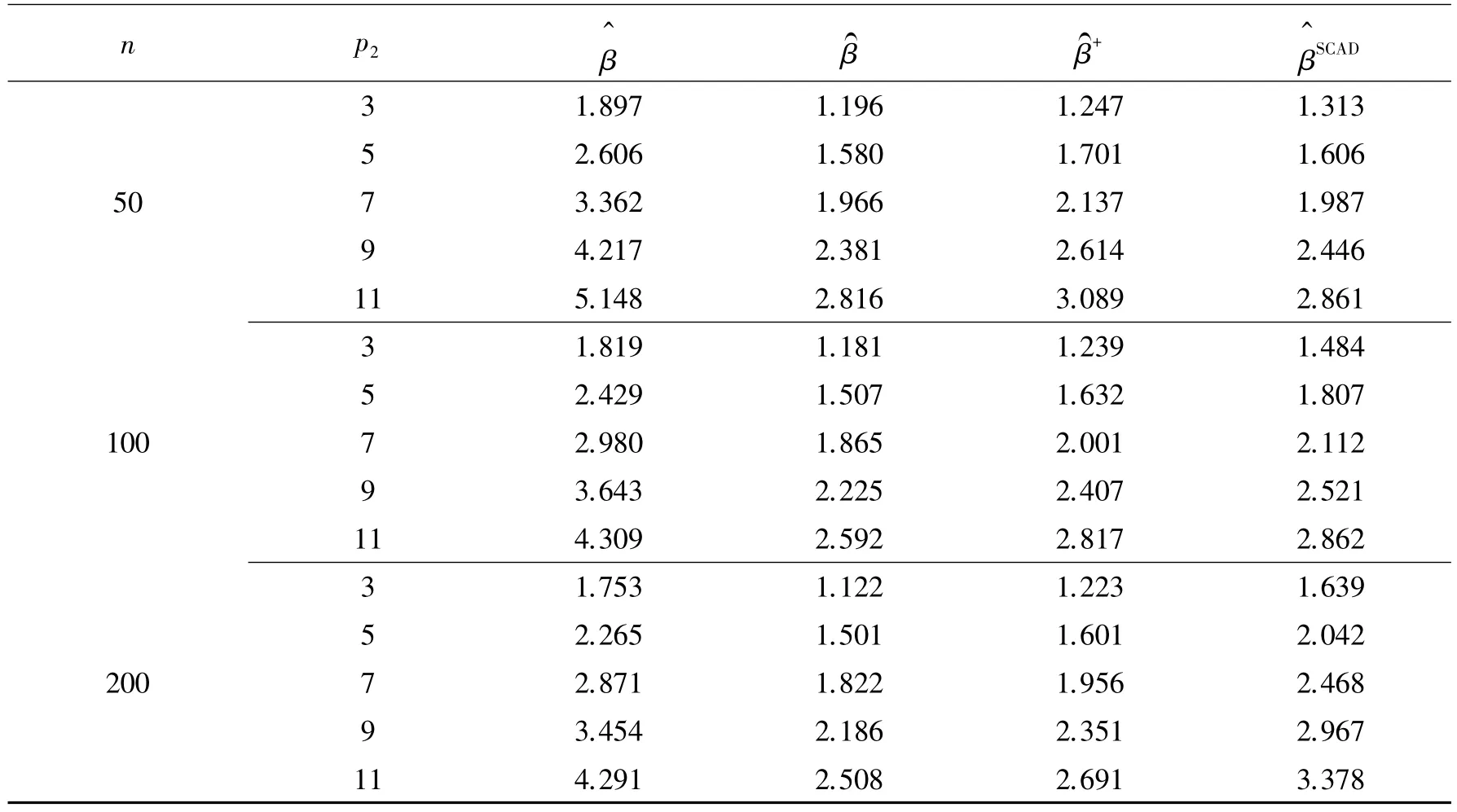
续表1
情况2原假设H0:Rβ=0不成立,或者δ≠0.表2为n=50,m=30时,SCAD惩罚估计和压缩差分别估计与的相对有效性.从表2中,得结论:当δ=0或者在δ在0附近时的相对有效性是最好的.但随着δ越远离0的相对有效性越来越小,SCAD惩罚估计的相对有效性是最大的.在p2一定时,压缩估计的相对有效性随着δ的增大而减小,SCAD惩罚估计的相对有效性有稍许的变动.当δ不变时,压缩估计的相对有效性和SCAD惩罚估计的有效性是p2的增函数.同时也发现的相对有效性总是优于的相对有效性.
表2 与的相对有效性(n=50,m=3)
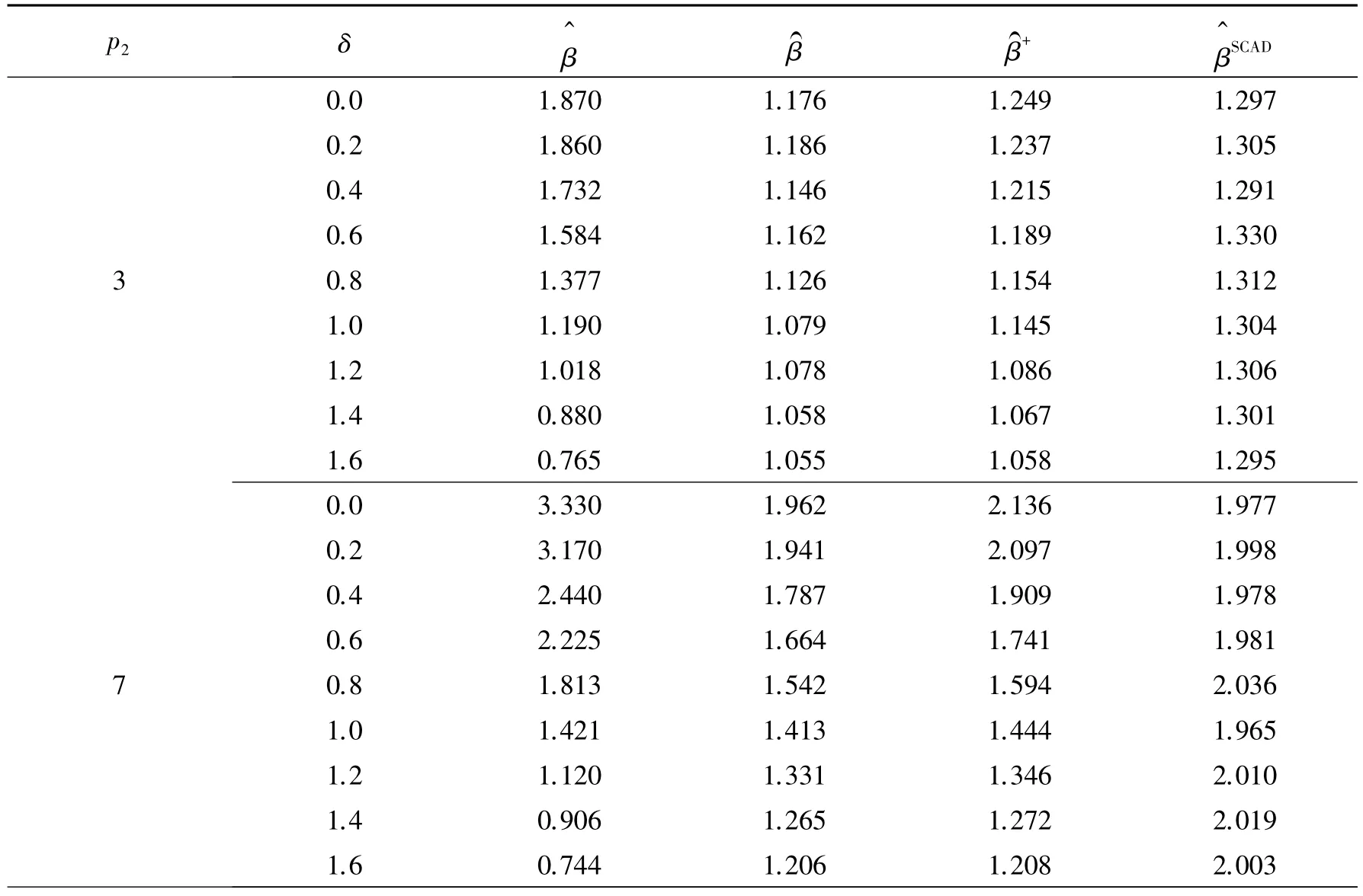
表2 与的相对有效性(n=50,m=3)
p2δβ^β)β)+β^SCAD0.0 1.870 1.176 1.249 1.297 3 0.2 1.860 1.186 1.237 1.305 0.4 1.732 1.146 1.215 1.291 0.6 1.584 1.162 1.189 1.330 0.8 1.377 1.126 1.154 1.312 1.0 1.190 1.079 1.145 1.304 1.2 1.018 1.078 1.086 1.306 1.4 0.880 1.058 1.067 1.301 1.6 0.765 1.055 1.058 1.295 7 0.0 3.330 1.962 2.136 1.977 0.2 3.170 1.941 2.097 1.998 0.4 2.440 1.787 1.909 1.978 0.6 2.225 1.664 1.741 1.981 0.8 1.813 1.542 1.594 2.036 1.0 1.421 1.413 1.444 1.965 1.2 1.120 1.331 1.346 2.010 1.4 0.906 1.265 1.272 2.019 1.6 0.744 1.206 1.208 2.003
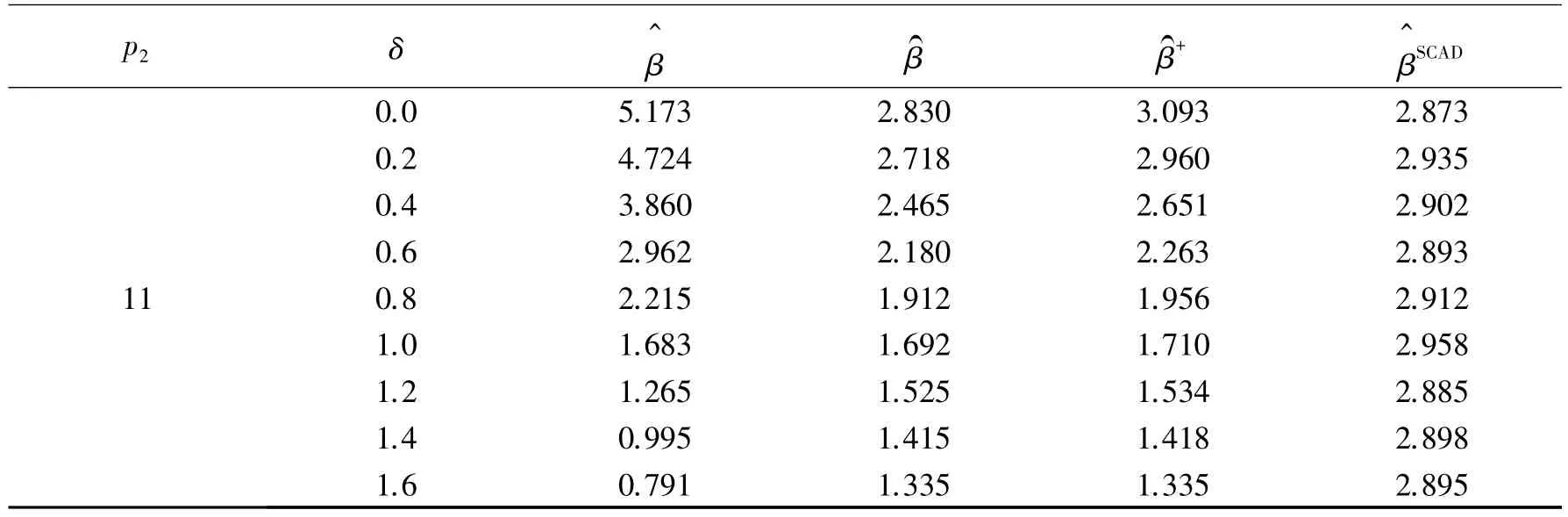
续表2
6 结论
基于部分线性回归模型,提出了压缩差分估计,并将改进的压缩差分估计与SCAD惩罚估计进行了比较,从第5部分的模拟中可以看到,压缩差分估计和SCAD惩罚估计都具有较好的性质.与传统的差分估计相比,压缩差分估计具有明显的优越性,并且SCAD惩罚估计在样本量越大的时候体现出的优越性也越明显.对于模型(1),如果选择差分技术,则可以有效避免带宽的选择.因此,对于部分线性回归模型,此处提出的差分压缩估计是一个较为有用并且简单的方法.
[1]HALL P,KAY JW,TITTERINGTON D M.Asymptotically Optimal Difference-based Estimation of Variance in Nonparametric Regression[J].Biometrika,1990(77):521-528
[2]STEIN C.Inadmissibility of the Usual Estimator for the Mean of a Multivariate Normal Distribution[J].Proceedings of the Third Berkeley Symposium on Mathematics and Statistical Probability,1956(1):197-206
[3]WANG L,BROWN L D,CAIT.A Difference Based Approach to the Semi-parametric Partial Linear Model[J].Electronic Journal of Statistics,2011(5):619-641
[4]AHMED SE,HOSSAIN S,DOKSUM K A.Lasso and Shrinkage Estimation in Weibull Censored Regression Models[J].Journal of Statistical Panning and Inference,2012(142):1273-1284
[5]SALEH A K,MD E.Theory of Preliminary Test and Stein-type Estimation with Applications[M].New York:John Wiley&Sons,2006
[6]FAN J,LI R.Variable Selection via Non-concave Penalized Likelihood and its Oracle Properties[J].Journal of the American Statistical Association,2001(96):1348-1360
SCAD and Improved Difference Estimation of Partially Linear Regression Model
GUO Xue-mei
(School of Mathematics and Statistics,Chongqing University,Chongqing 401331,China)
This paper considers the problem of estimating a vector of regression parameters in partially regression model.Differential shrinkage estimator with better properties is proposed.The SCAD penalties are applied to the partially linear regression model.Results of the differential shrinkage estimators and SCAD estimators are simulated by Monte Carlo and compared in strength and weakness.
difference estimation;partially linear regression model;SCAD;shrinkage estimators
O212
A
1672-058X(2015)09-0010-06
10.16055/j.issn.1672-058X.2015.0009.003
2015-01-11;
2015-03-20.
郭雪梅(1990-),女,重庆人,硕士研究生,从事参数估计和变量选择研究.

