关于确定θ2极小多项式的几个定理
胡怀兰(重庆师范大学数学科学学院,重庆401331)
关于确定θ2极小多项式的几个定理
胡怀兰
(重庆师范大学数学科学学院,重庆401331)
在已有定理的基础上,巧妙地利用初等数论的方法,得出在一些特定情况下由θ的极小多项式求得θ2的极小多项式的几个相关定理.这些定理对于确定域的判别式以及整基有重要作用.
极小多项式;代数整数;整系数多项式
1 关键符号、定义与引理
Z:{自然数,自然数的相反数};Q:有理数集;Z[x]:系数属于Z的多项式组成的集合;Q[x]:系数属于Q的多项式组成的集合.
定义1[1]代数数α叫做代数整数(简称作整数),如果存在一个系数属于Ζ的首1多项式f(x),使得f(α)=0.
引理1[2]设α为代数数,f(x)为α在Q上的极小多项式,则α为整数的充要条件是f(x)∈Z[x].
引理2[3]如果f(x)是Z[x]中的首1多项式,而g(x)∈Q(x)是f(x)的首1多项式因子,则g(x)∈Z[x].
2 主要定理与证明
定理1θ为代数整数,则θ2也为代数整数.
证明θ为代数整数,设它在Q上的极小多项式为
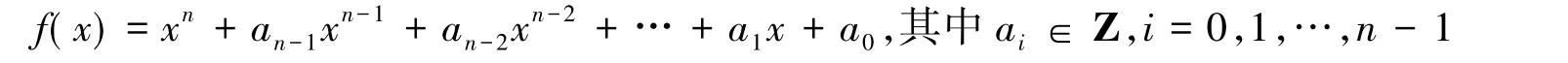
则
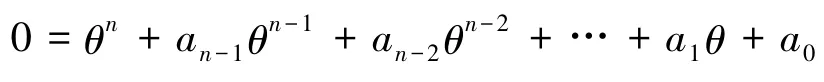
于是
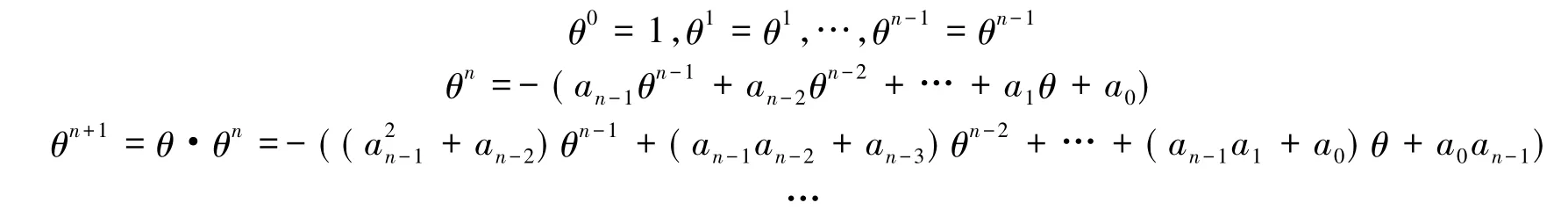
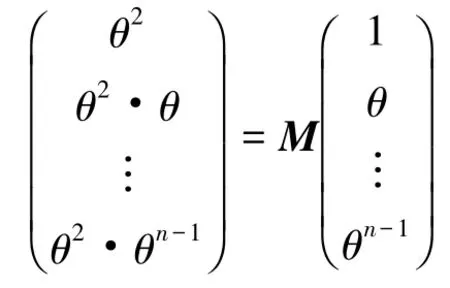
定理2代数整数θ为有理数,则θ∈Z,θ2∈Z,即θ2的极小多项式就为f(x)=x-θ2.

定理3代数整数θ不为有理数,其在Q上的极小多项式为f(x)=x2+px+q时,θ2的极小多项式
当p=0时,θ2+q=0,则g(x)=x+q即为θ2在Q上的极小多项式.
假设g(x)=x2-(p2-2q)x+q2在Q上在可约,即在Q上有根,而其有理根只可能为±1,±q,±q2,带入发现都不是解,从而在Q上不可约,即g(x)=x2-(p2-2q)x+q2为θ2在Q上的极小多项式.证毕.
定理4代数整数θ的极小多项式为f(x)=xn+kx+l,θ2的极小多项式为

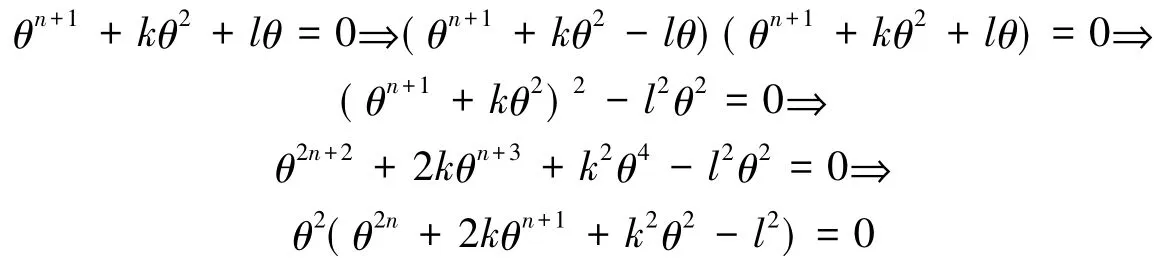
即θ2是整系数多项式的根,再根据Eisenstein判别法[1]或者其他有理系数多项式是否可约判定定理确定其是否可约.若在Q上不可约,即为θ2的极小多项式;若可约,由引理2,θ2的极小多项式h1(x)为的因式.综上所述且h1( x)∈Z[x].

即θ2是整系数多项式的根,若在Q上不可约,即为θ2的极小多项式;若可约,由引理2,θ2的极小多项式h2(x)为的因式.综上所述且 h2(x)∈Z[x].证毕.
[1]柯召,孙琦.数论讲义[M].北京:高等教育出版社,2001
[2]华罗庚.数论导引[M].北京:科学出版社,1979
[3]张德馨.整数论[M].哈尔滨:哈尔滨工业大学出版社,2011
Several Theorems on Determining the Minimal Polynomial ofθ2
HU Huai-lan
(School of Mathematical Sciences,Chongqing Normal University,Chongqing)
Based on the existing theorems,in some certain cases,this paper uses the method of elementary number theory to obtain several related theorems of theminimal polynomial ofθ2got from theminimal polynomial of θ.These theorems play an important role to determine the discriminant and integermatrix of domain.
minimal polynomial;algebraic integer;integer coefficient polynomial.
O156.1
A
1672-058X(2015)09-0043-02
10.16055/j.issn.1672-058X.2015.0009.011
2015-01-07;
2015-02-13.
胡怀兰(1990-),女,重庆巫溪人,硕士研究生,从事数论研究.

