一个带有干扰因子修正PRP共轭梯度法的全局收敛性*
陈洪敏(重庆师范大学数学学院,重庆401331)
一个带有干扰因子修正PRP共轭梯度法的全局收敛性*
陈洪敏
(重庆师范大学数学学院,重庆401331)
非线性共轭梯度法是解决大规模优化问题的一种非常有效的方法,提出了一个修正的PRP方法,该参数带有干扰因子,并证明了这一新的参数具有非负性,且在适当条件下,采用Wolfe线搜索,证明该算法具有全局收敛性.
共轭梯度法;强Wolfe条件;Wolfe条件;干扰因子;全局收敛性
1 基础知识
考虑如下的无约束极小化问题:

其中,f:Rn→R是连续可微函数,且其梯度可获得.
非线性共轭梯度法是求解此类问题的一种常用的有效方法,具有算法简便、存储需求小等优点,适用于求解大规模无约束优化问题.共轭梯度法的迭代格式为

其中dk为搜索方向,▽f(xk)简记为gk,βk是一个参数,不同的βk对应着不同的共轭梯度法,αk是通过适当的线搜索获得的步长,通常使用Wolfe线搜索、强Wolfe线搜索.
Wolfe线搜索条件为

强Wolfe线搜索条件为

其中0<δ<σ<1.
传统共轭梯度法的参数公式βk的计算公式有Hestenes-Stiefel(HS)[1],Fletcher-Reeves(FR)[2],Polak-Ribiere(PRP)[3],Dai-Yuan(DY)[4],它们的表达式分别为
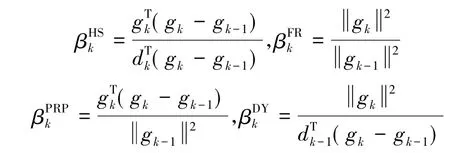

这种方法在适当条件下,分别证明算法在Wolfe和Grippo-Lucidi线搜索下是全局收敛的.文献[6]通过对参数βk加入干扰因子得到两个新的βk,公式如式(8):


文献[7]分析了PRP方法,认为限制其参数βk的非负性不仅对方法的全局收敛性起到至关重要的作用,而且能够很容易地保证算法的下降性;文献[8]证明了在充分下降条件被满足,且步长αk满足Wolfe线搜索条件的前提下,算法具有全局收敛性.在接下来的引理中证明了的非负性.
假设目标函数满足下面的假设:
2)目标函数f在Ω的某个领域N是连续可微的,且梯度函数是Lipschitz连续的,即存在常数L>0使得


对任意的x∈N.
证明记θk为gk和gk-1的夹角,即

因为ν≥1,故
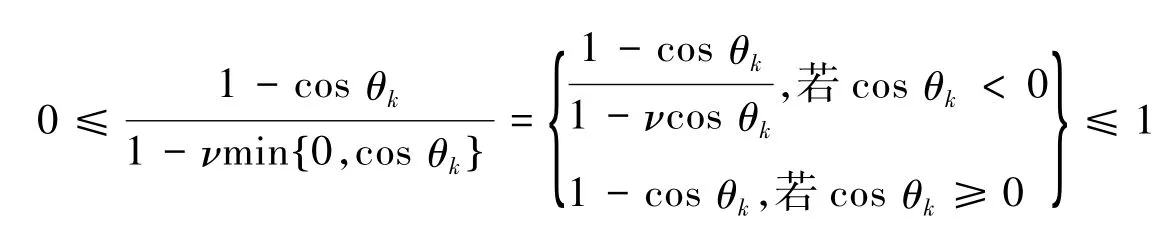
引理2(性质*)考虑形如式(2)(3)的方法,并且假设对任意的,则存在常数b>1,λ>0,使得对任意的k≥1都有
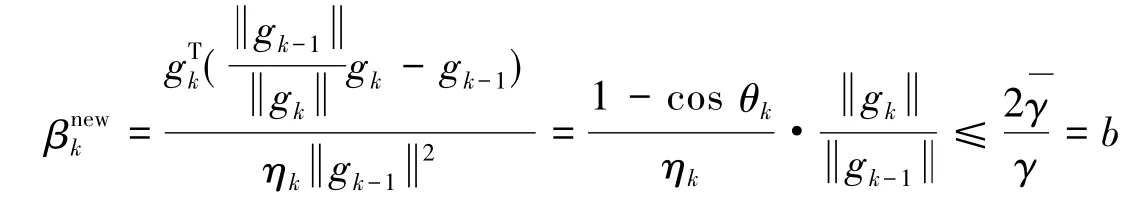
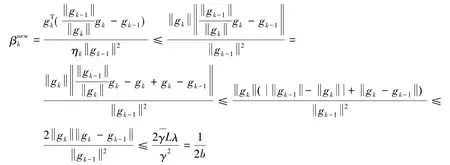

在共轭梯度法中,充分下降条件非常重要,其中假设new算法满足式(12).
引理3[8](zoutendijik条件)若假设1)2)成立,考虑形如式(2)(3)的方法,dk是下降方向,αk满足式(5)(6),则
引理4[8]若假设1)2)成立,考虑形如式(2)(3)的方法,αk满足式(5)(6),且满足充分下降条件式(12),若βk满足性质(*)且成立,则存在λ1>0,使得对任意的Δ∈N*和下标k0,都存在指,则
因为ν≥1,故标k≥k0,满足,其中表示的个数.
引理5[8]若假设1)2)成立,考虑形如式(2)(3)的方法,满足下面3个条件:(i)对任意的k≥1,都有βk≥0;(ii)算法采用Wolfe-power线搜索,满足zoutendijik条件,满足充分下降条件式(12);(iii)满足性质
定理1若假设1)2)成立,考虑形如式(2)(3)的方法,充分下降条件式(12)成立,αk满足式(5)(6),βk取.即new算法具有全局收敛性.
[1]HESTENESM R,STIEFEL E L.Method of Conjugate Gradient for Solving Linear Systems[J].Res Natl Bur Stand,1952(49): 409-436
[2]FLETCHER R,REEVESC.Function Minimization by Conjugate Gradients[J].Comput,1964(7):149-154
[3]POLAK B,RIBIEREG.Note Surla Convergence Des Meethodes de Directions Conjugees[J].Rev Fr Inf Rech Oper,1964,3(1): 35-43
[4]DAIY H,YUAN Y X.A Nonlinear Conjugate GradientMethod with a Strong Global Convergence Property[J].SIAM Optim,1999 (10):177-182
[5]黎勇.一类修正PRP共轭梯度法的全局收敛性及其数值试验结果[J].西南大学学报:自然科学版,2011,33(11):23-28
[6]JIANG X Z,JIAN J B.Two Modified Nonlinear Conjugate Gradient Methods with Disturbance Factors for Unconstrained Optimization[J].Nonlinear Dynamics,2014,77(1-2):387-394
[7]POWELLM JD.NonconVex Minimization Calculations and the Conjugate Method[J].Lecture Notes in Mathematics,1984,10 (66):122-141
[8]GLIBERT JC,NOCEDAL J.Global Convergence Properties of Conjugate GradientMethod for Optimization[J].SIAM Optim,1992 (2):21-42
Global Convergence Property of a Modified PRP Conjugate Gradient Method with Disturbance Factor
CHEN Hong-m in
(School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China)
The nonlinear conjugate gradientmethod is a very effective iterativemethod for solving large-scale optimal problems.In this paper,amodified PRP conjugate gradientmethod with disturbance factor is proposed and non-negative property of the formula is proved.Under suitable conditions,the global convergence of the algorithm with theWolfe line search is discussed.
conjugate gradient method;strong Wolfe condition;Wolfe condition;disturbance factor; global convergence
O224
A
1672-058X(2015)09-0001-04
10.16055/j.issn.1672-058X.2015.0009.001
2014-12-11;
2015-02-24.
国家自然科学基金(10771003).
陈洪敏(1988-),女,安徽阜阳人,硕士研究生,从事最优化理论与算法研究.

