带有混合约束的特殊三次规划问题的全局最优性充分条件

周莉，李国权(重庆师范大学数学学院，重庆401331)

带有混合约束的特殊三次规划问题的全局最优性充分条件

周莉，李国权
(重庆师范大学数学学院，重庆401331)

利用拉格朗日函数和L-次微分的方法，研究了带有双值和不等式约束的特殊三次规划问题的全局最优性充分条件;首先刻画出该类三次规划问题的拉格朗日函数的抽象次微分，得到了特殊三次规划问题的全局最优性充分条件;然后，举例说明利用所给出的全局最优性充分条件判定当前可行解就是全局最优解是有效的.

三次规划;拉格朗日函数;L-次微分;全局最优性充分条件

1　预备知识

全局最优化在数学规划理论中是一个重要的研究领域，它的理论研究之一是怎样刻画一个全局优化问题的解，全局最优充分性条件是用来说明一个解是全局最优解的一个重要理论依据.三次规划数学模型在三次多项式近似优化［1］、凸优化［2］、工程设计和结构优化［3］等领域有着广泛的应用.而三次问题的研究成果可以应用到二次规划问题［4］，文献［5-7］对含有箱子或二元约束的特殊三次规划问题的全局最优性条件进行了研究，取得了一定的进展.此处是基于文献［5］和文献［8，9］，利用拉格朗日函数和L-次微分的方法，研究了带有双值和不等式约束的特殊三次规划问题的全局最优性充分条件.同时给出例子说明给出的最优性条件能有效地用于确定给定的三次极小化问题的全局极小值，所得结果改进和推广了文献［4，5］中的相应结果.

R表示实线性空间，Rn表示n维欧几里得空间.对于向量x，y∈Rn，x≥y⇔xi≥yi，i=1，2，…，n，记号A≥是半正定矩阵.

考虑如下三次规划问题:

定义1［10］(L-次微分)设则称l为f在x0处的L-次梯度，f在x0的所有L-次梯度的集合称为f在x0的L-次微分.

注:若L是所有线性函数所成的集合，f是一个下半连续的凸函数，则，这里指一般凸分析意义上的凸函数的次梯度.

2　主要结论

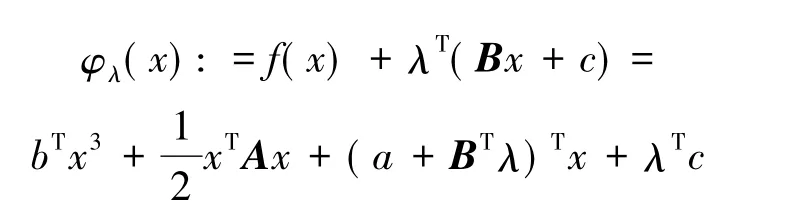
先考虑如下问题:

令L为一些特殊的三次函数作成的集合:

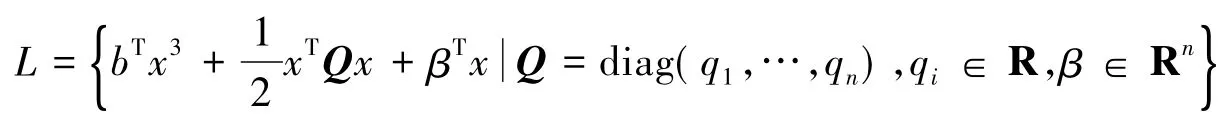
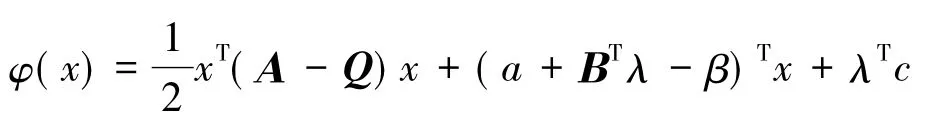
证毕.

分两种情况讨论:

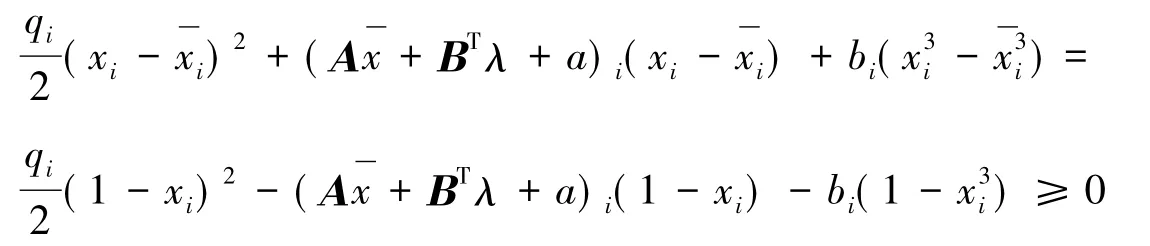
例1

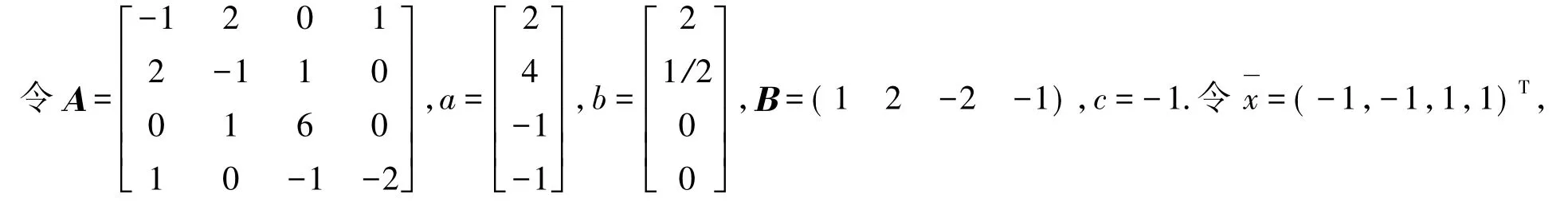
ΒTx+c=0，取λ=1≥0，则，则，取则Q= diag(－3，－6，1，－6)，且满足Α－Q≥0，对于任意的，且有，则x为问题的全局极小点.

例2

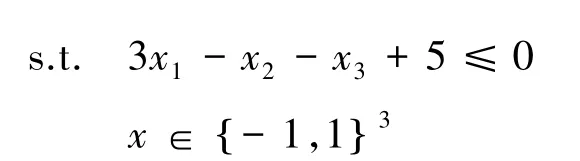
［1］CANFIED R A.Multipoint Cubic Surrogate Function for Sequential Approximate Optimization［J］.Structural and Multidisciplinary Optimization，2004(27):326-336

［2］NESTEROV Y.Accelerrating the Cubic Regularization of Newton’s Method On Convex Problem［J］.Mathematical Programming，2008，12(1):159-181

［3］LIN C S，CHANG P R，LUTH JY S.Formulation and Optimization of Cubic Polynomial Joint Trajectories for Industrial Robots［J］.IEEE Transaction on Automatic Control，1983，28(12):1066-1074

［4］WU Z Y，YANG Y J，BAIF S，et al.Necessary Optimality Conditions and Optimization Methods for Quadratic Knapsack Problem［J］.Journal of Optimization Theory and Applications，2011(151):241-259

［5］ZHANG X M，WANG Y J，MA W M.Global Sufficient Optimality Conditions for a Special Cubic Minimization Problem［J］.Mathematical Problems in Engineering，2012(2012):1-16

［6］周雪刚.具有超矩形约束的三次规划的全局最优性条件［J］.重庆师范大学学报:自然科学版，2014，31(4):21-25

［7］WANG Y J，LIANG Z A.Global Optimality Conditions for Cubic Minimization Problem with Box or Binary Constraints［J］.Journal of Global Optimization，2010(47):583-595

［8］WU Z Y，JEYAKUMAR V，RUBINOV A M.Sufficient Conditions for Global Optimality of Bivalent Nonconvex Quadratic Programs with Inequality Constraints［J］.Journal of Optimization Theory and Applications，2007(133):123-130

［9］张甲，田志远，李敬玉.一类非凸二次规划的全局最优性条件［J］.青岛大学学报，2010，23(3):20-23

［10］李国权，吴至友.带有二次约束的一些非凸二次规划问题的全局最优性条件［J］.重庆师范大学学报:自然科学版，2008，25(3):1-4

The Global Optimal Sufficient Conditions for a Special Cubic Minimization Problem with Mixed Constrains

ZHOU Li，LIGuo-quan
(School of Mathematical Sciences，Chongqing Normal University，Chongqing 401331，China)

By employing Lagrangian function and L-subdifferential approach，the global optimal sufficient conditions for a class of cubic programming problem involving bivalent and inequality constrains is researched.Firstly，the abstract subdifferential for Lagrangian function of the class of cubic programming problems is calculated explicitly.Then some global optimal sufficient conditions for cubic programming problem with bivalentand inequality constrains are obtained.Finally，some examples are given to illustrate the optimality conditions.

cubic program;Lagrangian function;L-subdifferential;global optimal sufficient conditions

O224

A

1672－058X(2015)09－0016－04

10.16055/j.issn.1672－058X.2015.0009.004

2014－12－04;

2015－01－04.

周莉(1990-)，女，重庆万州人，硕士研究生，从事全局优化理论与方法研究.