非奇异M矩阵Hadamard积的特征值界的新序列*
蒋建新,李艳艳(文山学院数理系,云南文山663000)
非奇异M矩阵Hadamard积的特征值界的新序列*
蒋建新,李艳艳
(文山学院数理系,云南文山663000)
利用非奇异M矩阵A的逆矩阵A-1元素单调的上下界序列和改进的圆盘定理,得到了M矩阵B与A-1的Hadamard积以及最小特征值下界单调递减的新估计式.
M矩阵;Hadamard积;最小特征值;下界
关于非奇异M矩阵A的逆矩阵A-1与M矩阵B的Hadamard积的最小特征值下界的研究,已得到许多估计式[1-6].但这些估计式有些涉及矩阵的特征值,有些涉及A-1的元素,有些又涉及A的谱半径,当矩阵阶数较大时计算比较困难.此处利用非奇异M矩阵A的逆矩阵A-1元素单调的上下界序列和改进的圆盘定理,得到了下界单调递减的一系列新估计式.这些估计式只与矩阵的元素有关,当迭代次数较高时,几乎可以逼近真值.
1 预备知识
首先引入一些记号:

其次,给出一些定义和引理.
定义1[1]设,如果则称A为Z矩阵.
定义2[1]设为Z矩阵,若A可表示为,其中,则称A为M矩阵,当α>ρ(P)时,称A为非奇异M矩阵,非奇异M矩阵的集合用Mn表示.
定义3[1]σ(A)={λ1,λ2,…,λn}表示矩阵A=(aij)∈Cn×n的n个特征值λ1,λ2,…,λn组成的集合,称为A的谱,A的最小特征值记作τ(A)=min{Re(λ):λ∈σ(A)}.
定义4[1]设称为A和B的Hadamard积.
引理1[1]若A=(aij)∈Rn×n是M矩阵,则存在正对角矩阵D,使D-1AD是严格对角占优矩阵,也是M矩阵.
引理2[1]设A,B,C,D∈Rn×n,其中C,D是对角矩阵,则

引理3[2]设A=(aij)∈Cn×n,x1,x2,…,xn是一组正实数,则A的所有特征值包含在复平面C的如下区域中:

引理4[3]设A=(aij)∈Rn×n是行严格对角占优的M矩阵,则i,j∈N,j≠i,t=1,2,…,有式(1)(2)成立:
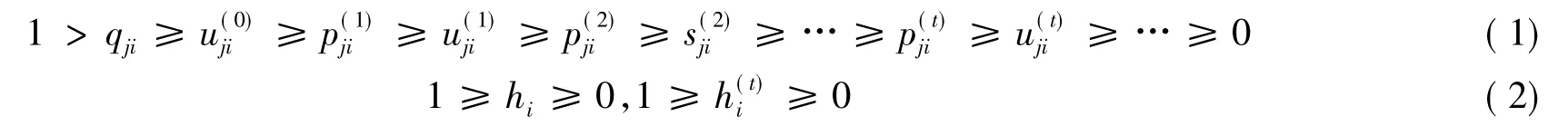
引理5[3]设A=(aij)∈Rn×n是行严格对角占优M矩阵,则A-1=(βij)存在且有下列不等式(3)成立:
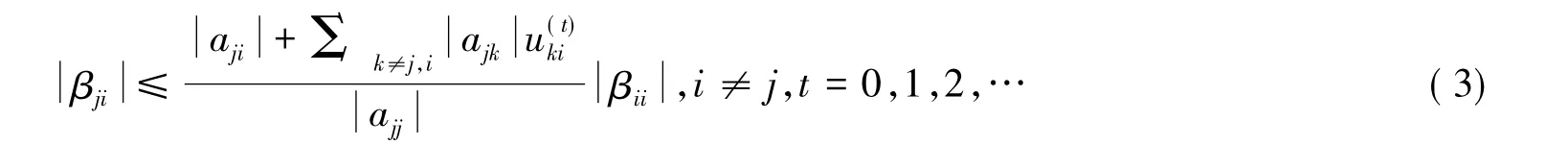
2 主要结果
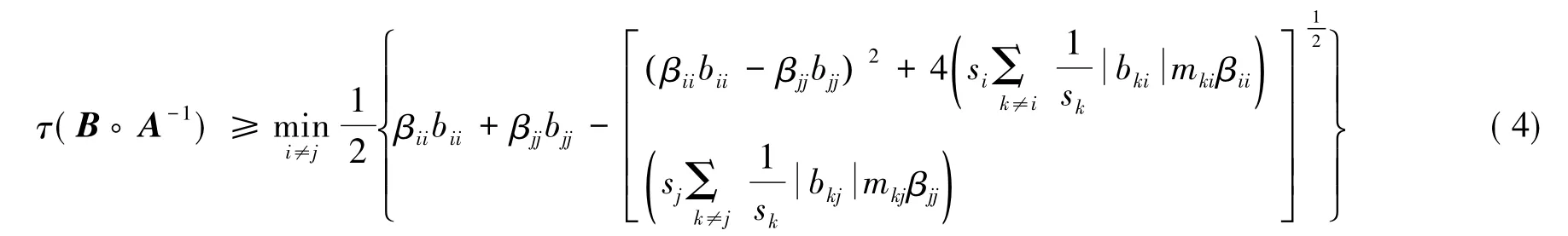

又因为

则有

化简整理得

2)若A,B有一个可约,类似文献[5]中定理2.2.2的证明知此时定理1也成立.
3 数值例子
假设

此例进一步说明了所得结果的有效性.
[1]陈景良,陈向晖.特殊矩阵[M].北京:清华大学出版社,2000
[2]王德凤.矩阵Hadamard积与Fan积的最小特征值与谱半径界的估计[D].昆明:云南大学,2011
[3]赵建兴.M-矩阵最小特征值估计及其相关问题研究[D].昆明:云南大学,2014
The New Sequence of the Eigenvalue Bounds of the Hadamard Product of Nonsingular Matrix
JIANG Jian-xin,LIYan-yan
(Department of Mathematics and Physics,Wenshan University,Wenshan 663000,China)
By using the upper and lower bounds on themonotone sequence for inversematrix A-1elements of nonsingular M matrix A and improved disk theorem ofmatrix,this paper obtains the new estimator of theminimum eigenvalue bounds decreasingmonotonically of Hadamard product of M matrix B and A-1.
matrix;Hadamard product;minimum eigenvalue;lower bound
O151.2
A
1672-058X(2015)09-0020-03
10.16055/j.issn.1672-058X.2015.0009.005
2015-03-13;
2015-04-02.
云南省教育厅科学研究基金项目(2013Y585);文山学院重点学科数学建设项目(12WSXK01).
蒋建新(1981-),男,讲师,硕士,从事矩阵理论及其应用研究.

