高速飞行器结构气动热计算与温度场模拟

王志超，张 龙，姚 琳

(南京理工大学机械工程学院，南京 210094)

当飞行器在大气中以超声速、高超声速飞行时，空气受到剧烈压缩和黏性阻滞，在飞行器表面边界层内的气流产生强烈的摩擦，气流速度降至壁面，将动能不可逆转地变为热能，从而引起附面层内温度迅速升高，飞行器表面温度也随之升高，这就是高速飞行器的气动加热现象［1］。飞行速度越高气动加热现象越严重，飞行器表面温度过高，不仅使飞行器结构的强度减弱、刚度下降，还会在飞行器结构内部产生热应力、热变形，甚至过高的温度会影响设备舱内仪器的工作性能，因此对高速飞行器的气动加热及结构内部的温度场分布进行研究，是高速飞行器热防护设计中必须重视的问题。

计算流体力学在气动力及气动热的计算中起着越来越重要的作用，由于超声速粘性流动的复杂性，气动热的数值模拟是十分困难的，在计算中受数值格式、网格分布、收敛过程等各方面因素的影响，因此对气动热的计算还远没有达到计算气动力那样的水平［2］，再加上数值计算对计算机要求高，耗时长，尤其当考虑湍流、转捩等问题时很难建立精确的数学模型［3］。

因此本文选用一种既能满足工程要求，同时使用起来又简洁高效的工程算法来计算飞行器表面的热流密度分布情况，并结合有限元方法进行飞行器结构的瞬态热传导分析，来预测飞行器结构在气动热环境下的温度分布，为飞行器的结构设计、热防护设计、材料选择以及飞行安全性评估提供参考依据。

1 基础理论

1.1 牛顿热流公式

飞行器在气动加热过程中，边界层内传热是典型的对流传热过程，工程中通常采用牛顿冷却公式来计算对流传热产生的热流量［4］q:

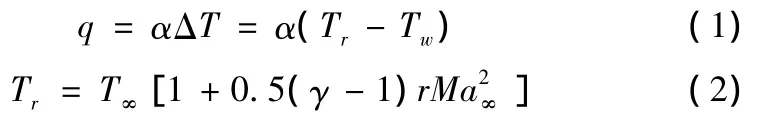
α表示对流换热系数，Tr为恢复温度，Tw为壁面温度，r为恢复因子，对于层流边界层，一般取r =，湍流时建议取r=Pr1/3，Pr为普朗特数，γ为比热比，带下标∞的参数表示来流参数，由于边界层内热物性参数是变化的，这就给α的求解带来了困难，在工程应用中，一般通过对气体性能参数的各种假设，来对公式进行修正，应用最多的是参考温度法。

参考温度法是假设高速边界层和低速边界层结构相同，直接利用低速不可压缩的公式在某一参考温度下计算流体特性，从而将低速不可压缩流的摩擦系数公式推广应用于高速可压缩流中，参考温度法有很多种，以埃克特(Eckert)参考温度方法应用最为广泛［5］:

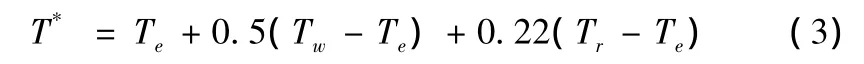
式(3)中带下标e的参数为边界层外缘气流参数。

1.2 驻点区热流密度计算

对驻点热流密度本文采用Kemp-Riddell公式:

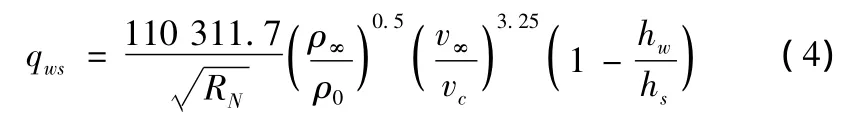
式(4)中:ρ0=1.225 kg/m3;vc=7900 m/s;RN为驻点曲率半径(m);qws为驻点热流密度(kw/m2);hs为滞止焓值;hw为壁面焓值。

1.3 非驻点区热流密度计算

非驻点区的热流密度的计算采用Lees钝体层流热流分布公式:

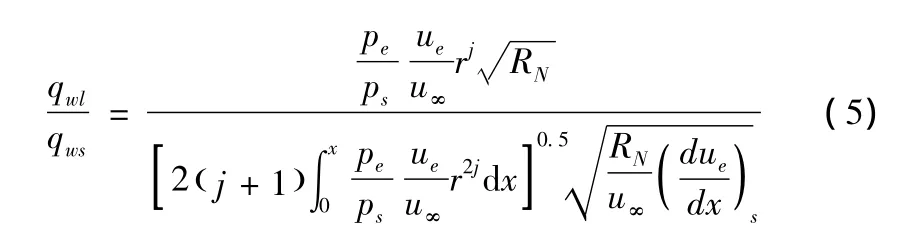
该公式从高冷壁假设出发，认为驻点物面上的焓梯度与驻点相同，该公式得出的结果同地面试验有着良好的一致性。式中平面二维流动时j=0，轴对称流动j=1;下标s表示驻点参数;qwl表示表面热流密度。利用等熵外流条件和修正牛顿压力分布，可以的到球面和锥面热流密度分布的解析表达式［6］。

在半球上的表达式:

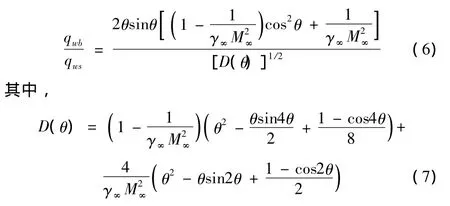
其中，qwb表示球头部热流密度，θ是从轴线测起的圆心角。在球锥锥面上的表达式:

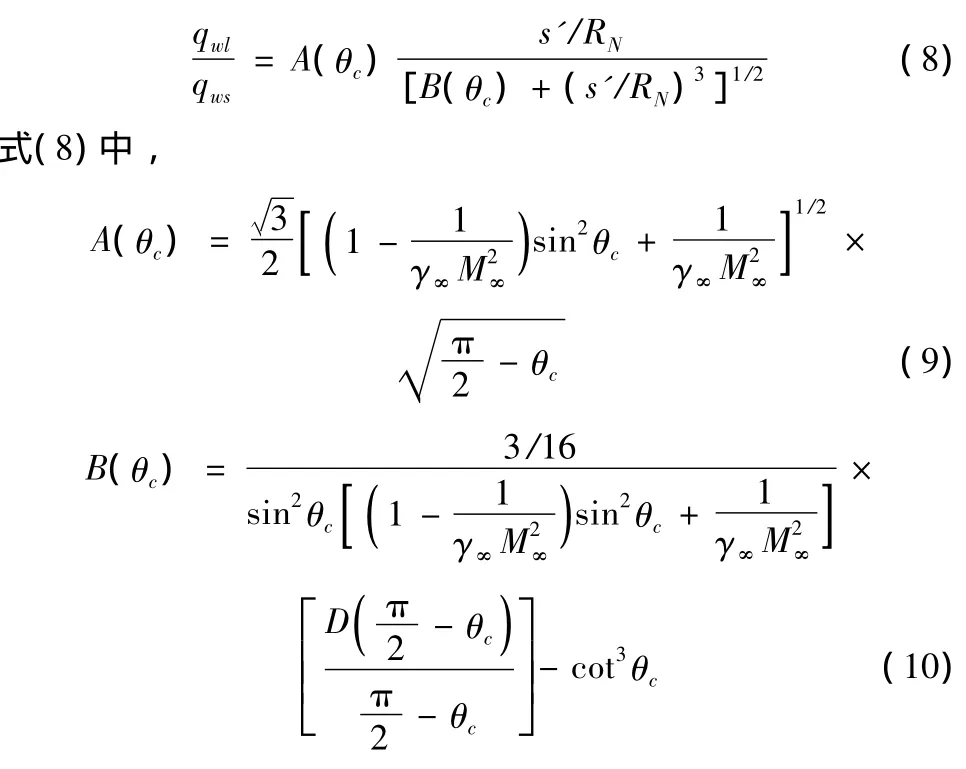
其中，θc为半锥角;s'为从虚构的锥顶点量起沿锥面的距离。

应用参考温度方法可得到考虑壁温影响的热流密度分布公式:

式(11)中 ρ*，μ*和分别由当地物面压力和相应参考温度给定。

体现现代学徒制特色既然是师徒制评价体系，评价的主体首先应该是徒弟和师傅，同时学校派出的指导老师也应积极参与到评价中来，社会第三方评价更是客观评价师徒制教学效果的力量，不同的评价主体以不同的侧重对师徒制教学效果给出不同的评价，互相印证得到比较公平客观的结果。因此评价主体概括起来就应包括师傅评价、学生自评、学生互评、导师评价、认证机构评价、社会用人单位评价和家长评价。

1.4 结构温度场控制方程

由气动加热引起的热交换中，流场与飞行器结构之间的对流换热占主导地位，再通过热传导将热量传导至飞行器结构内部，蒙皮向内部传热方程由傅里叶定律可知［7］:

式(12)中:λ为导热系数;ΔT为温差。

在笛卡尔坐标系中三维非稳态导热微分方程的一般形式为

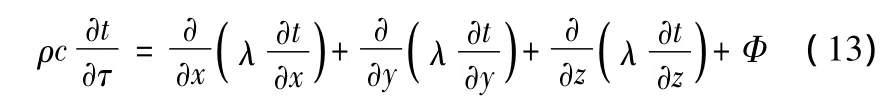
其中 ρ、c、λ、Φ及τ分别为微元体的密度、比热容、单位时间内单位体积中内热源的生成热及时间。

1.5 结构温度场分析

本文采用有限元方法进行结构的传热分析，通过建立结构的有限元模型，用上文所述方法求得的热流密度作为边界条件，对受热部件进行瞬态热传导分析，结构温度场有限元方程为

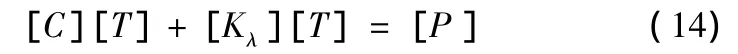
式(14)中，［C］为热容矩阵;［T］为结构温度矩阵;［Kλ］为热传导矩阵;［P］为温度载荷矩阵。

计算瞬态温度场的有限元基本方程:

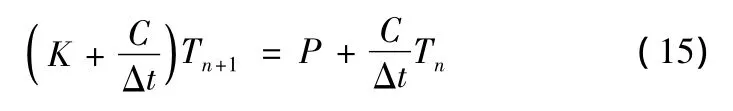
2 弹头结构热分析

2.1 算例验证

模拟结构的温度场分布是否合理，与结构所选边界条件是否准确密切相关，为了验证前文所述热流边界计算方法的正确性，本文计算了有详尽实验数据的钝双锥模型的高超声速绕流情况。模型头部曲率半径 RN=3.835 mm，前锥长L1=69.55 mm，模型总长 L=122.24 mm，前锥半锥角为12.84°后锥半锥角为 7°来流条件:Ma∞=9.86，P∞=59.92 Pa，T∞=48.88 K，Tw=300 K。

图1为钝双锥在0°攻角下，采用前文所述方法计算的迎风面热流密度，并与文献［8］中的实验结果进行了对比。从图中可以看出，计算值与实验值能够很好的吻合，同时体现出了双锥在交接处热流密度的变化情况。因此，在钝头锥表面热流密度计算方面，本文采用的方法具有较高的精度，可以为高速钝头体的热分析提供准确的热流边界条件。

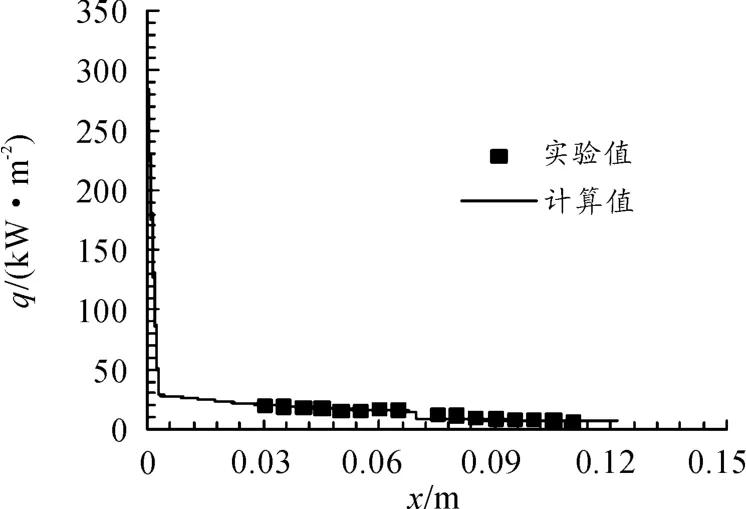
图1 钝双锥0°攻角下迎风面热流分布

2.2 弹头热环境分析

本文以某高速导弹弹头为模型，采用前文所述方法进行弹头的热环境分析，得出弹头表面热流密度分布，将其为后续传热分析的热边界条件施加在弹头上。弹头模型为钝锥型弹头，球头半径为5mm，椎体半锥角为12°，来流条件为Ma∞=3.5，T∞=216.65 K，ρ∞=0.08803 kg/m3，计算得出弹头热流分布如图2所示，从图2中可以看出热流密度在球头驻点处最大，并沿球头表面迅速下降，在锥面上热流密度并不是很高，变化幅度也不是很大，也就是说在驻点处气动加热最严重，因此球头部分是我们进行热分析关注的重点。

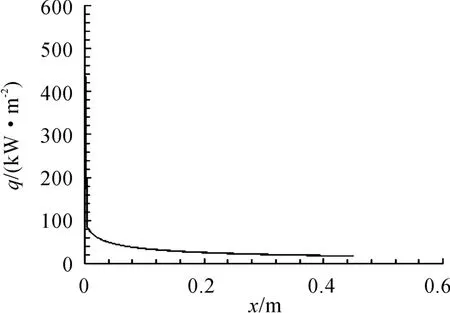
图2 模型热流密度

2.3 弹头温度场模拟

本文采用有限元法，对弹头进行温度场模拟，热流边界采用上文计算得出的热流密度，弹头材料为钛合金ZTC4，考虑钛合金热物性参数的非线性效应，材料参数如表1所示，有限元模型采用四面体传热单元，分析时间为50 s，对弹头模型进行瞬态温度场分析。

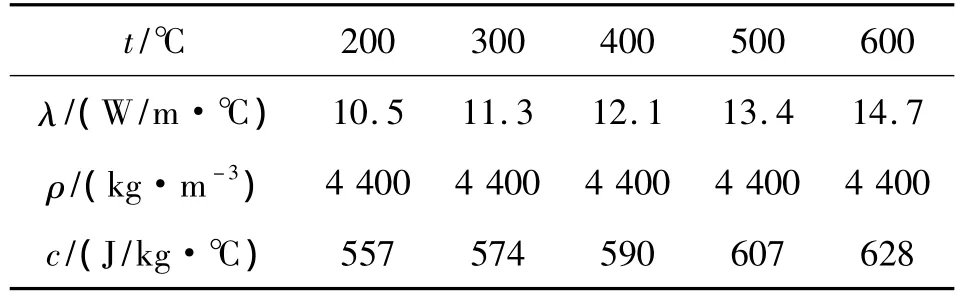
表1 ZTC4热物性参数

图3～图5为弹头在给定热流边界的条件下，导弹飞行50 s的过程中不同时刻弹头的温度分布情况，从图中可以看出，随着时间的推移，高温区不断的由弹头驻点部位向尾部推移，但从总体来看弹头球头部位，即弹头驻点附近区域温度始终保持最高，而弹头锥面上的温度相对较低，且分布比较均匀。

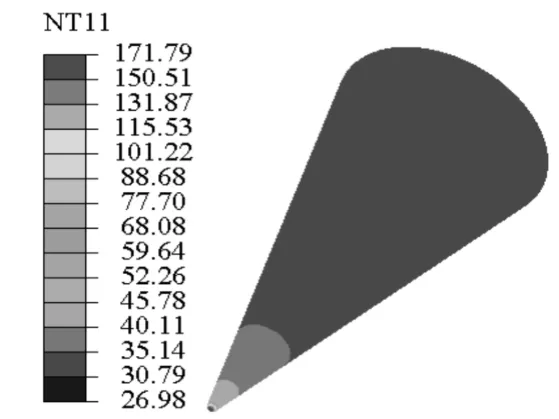
图3 t=1 s时温度场

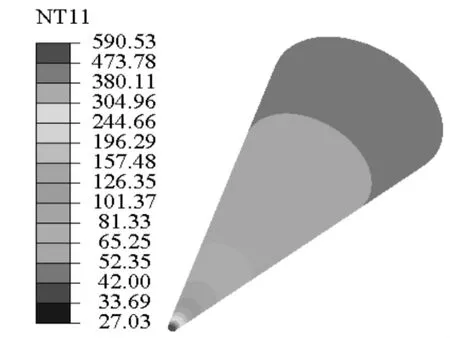
图4 t=30 s时温度场

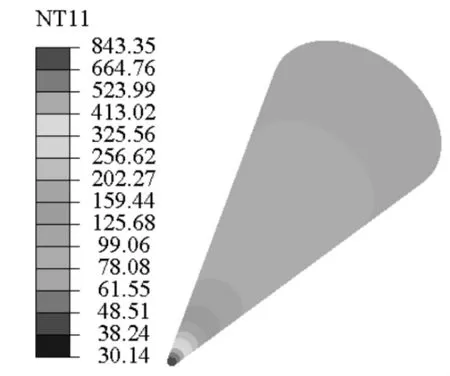
图5 t=50 s时温度场

在50 s时刻沿弹头表面温度变化趋势如图6所示，在弹头驻点部位温度高达843.35℃，而沿球头表面温度迅速下降至200℃左右，弹头这一部位温度梯度最大，这与上节计算所得到的热流密度分布情况相对应。图7为沿弹头轴线分布，距弹头驻点距离为0 mm、24 mm、71 mm处节点温度随时间的变化情况，驻点处温度从一开始的27℃持续升高到843.35℃，在气动加热的前10 s温度上升最快，10 s后温度上升有所减缓，在24 mm和71 mm处节点温度变化范围明显减小，最高温度分别为329℃和93℃，且由曲线趋势可看出24 mm和71 mm处节点的温升有明显的滞后现象，这是由于在气动加热的前期温度还没有传递至弹头内部造成的。

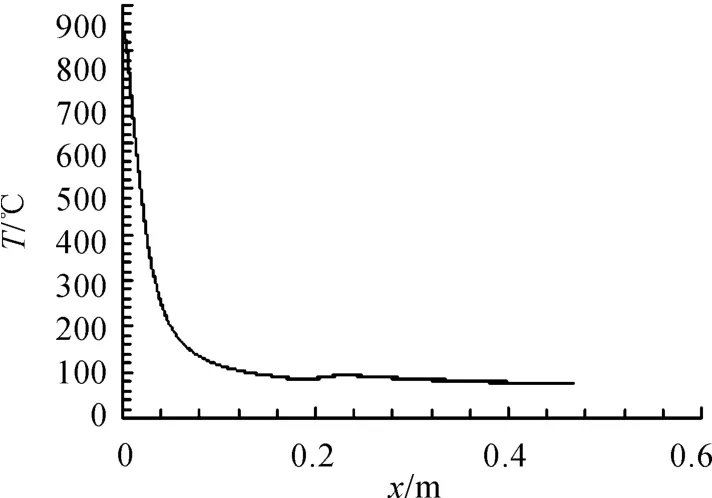
图6 50 s时刻沿弹头表面温度分布

图7 沿弹头轴线不同位置温度分布

从弹头表面热流密度的计算到整个弹头的温度场模拟，不难发现球头部位的气动加热最严重，在导弹的长时间高速飞行过程中势必给导弹的飞行安全带来隐患，因此必须加强对球头部位的热防护工作，通过本文的计算与分析可以为导弹的热防护设计提供可靠的依据。

3 结束语

通过工程算法来计算高速飞行器表面的热流密度分布情况，并与钝双锥模型的气动加热实验数据进行对比，证明了所选则工程算法的可行性，利用该方法求得钝锥型弹头的热流密度分布，作为弹头瞬态温度场模拟的边界条件，采用有限元方法求得不同时刻弹头结构的温度场分布，在求解过程中考虑了材料热物性参数的非线性效应。分析的目的在于为飞行器的结构设计、热防护设计、材料选择以及飞行安全性评估提供参考依据。通过分析可知，弹头驻点附近区域气动加热现象最严重，应作为热防护设计的重点对象。

［1］乐发仁，杨军，姜贵庆，等.微重力火箭气动加热计算［J］.固体火箭技术，2003，26(1):1-3.

［2］邱春图，陈振中.高超声速飞行器热结构设计分析技术研究［J］.飞机设计，2012，9(2):6-14.

［3］陈鑫，刘莉，李昱霖，等.高超声速飞行器翼面气动加热的工程计算方法［J］.弹箭与制导学报，2013，33(3):133-136.

［4］车竞，唐硕，何开锋.类乘波体飞行器气动加热的工程计算方法［J］.弹道学报，2006，18(4):93-96.

［5］Eckert R G.Engineering relations for friction and heat transfer to surface in high velocity flow［J］.Journal of Aerospace Science，1955:585-587.

［6］Lees.Laminar heat transfer over blunt nosed bodies at hypersonic flight speeds［J］.Jet Propulsion，1956，26(4):259-269.

［7］雷桂林，陈方，张胜涛，等.持续气动加热环境下的结构热载荷分析与应用［J］.科学技术与工程，2013，13(12):3343-3349.

［8］Miller C G.Experimental and predicted heating distributions for biconics at incidence in air at Mach 10［R］.NASA TP-2334，1984，11:16-29.