数形结合法在医学院校《高等数学》教学中的应用

王晓娜　丁丹

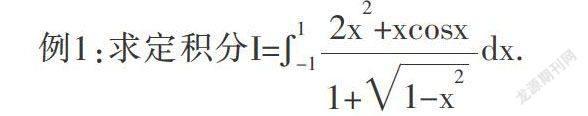
摘 要： 本文深入分析了医学院校《高等数学》课程的教学现状及存在的问题，基于此，提出了一种提高教学效率的优化教学方法——“数形结合法”.该方法把抽象的数学语言和直观的几何图形联系起来，将《高等数学》教学中抽象的问题直观化，复杂的问题简单化.

关键词： 数形结合 高等数学 教学方法 医学院校

一、引言

《高等数学》课程的主要内容包括：微积分、空间解析几何、微分方程，其中微积分占主要部分.微积分与其说是数学史上，不如说是人类科学史上的重大发明.美国著名数学家柯朗指出：“微积分或数学分析，是人类思维的伟大成果之一，它处于自然科学与人文科学之间的地位，使它成为高等教育的一种特别有效的工具，这门学科乃是一种憾人心灵的智力奋斗的结晶.”

近年来，《高等数学》与医学之间的联系日益显现，其思想和方法广泛应用于医学科学领域，包括基础研究、临床应用、检测诊断等方面[1].许多医学课程的学习和应用也需要一定的数学基础，如：细胞生物学、数理医药学、生物化学、分子生物学等课程[2].但在实际教学过程中，医学院校《高等数学》课程的教与学存在一定的难度.基于此，医学院校教师必须改变过去传统的教学方法和教学手段，采取多样的教学方式，为学生营造良好的学习氛围，激发学生的学习兴趣.

实践验证，在《高等数学》教学中采用“数形结合”是比较有效的方法，我国著名的数学家华罗庚曾说：“数形结合百般好，割裂分家万事休.”“数”与“形”反映了事物两个方面的属性，“数形结合法”是指把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”的方法，把抽象思维与形象思维结合起来，可以使《高等数学》教学中的复杂问题简单化、抽象问题具体化，从而达到优化其解题途径的目的.

二、医学院校《高等数学》课程的教学现状及问题分析

目前，《高等数学》课程是理工科院校本科学生的一门重要基础课程，是初等数学的发展，也是实际应用的有力工具[3].同时，它也是医学院校药学，药物制剂，以及生物医学工程等专业必修的数学课程之一，它作为一种众多学科共同使用的精确的科学语言，对学生后继课程的学习及思维素质的培养起着其他学科无法比拟的重要作用[4].

《高等数学》课程的显著特点是其具备严谨的逻辑性、高度的概括性和抽象性，有助于培养学生的逻辑思维能力、抽象思维能力、创新精神和创新能力，有利于其今后创造性地开展科学研究工作.这一特性对于医学生的专业学习和专业发展至关重要，因此，《高等数学》课程是医学院校必须重视的一门基础课程.但目前各医学院校在《高等数学》课程的教学中存在一定的问题，其中主要包括以下方面.

（一）教学内容安排一刀切，不符合客观需求.

目前我国医学院校部分专业采取文理兼收的模式，部分医学生本身数学基础比较薄弱.而医学院校《高等数学》课程在教学内容的安排上，大多比照高等院校理工科专业的教学安排，套用其教学日历，在教学内容上没有什么改变和删减.这对医学生来说，不但增加了其学习《高等数学》的难度，而且很显然，这种一刀切的教学内容安排也不符合医学院校实际招生情况的客观需求.

（二）教学学时紧张，增大了教学难度.

医学院校的教学工作具有很强的专业特性，医学专业课程和专业实践课程在教学中占了绝大部分教学学时.这就存在医学院校对《高等数学》等类课程学时安排不足的现象，由此导致，一方面教师在教学过程中觉得学时不够，不能对教学内容进行深挖和引申，不能很好地优化课程教学，另一方面教师在讲授过程中进度较快，采用重点和难点详细讲解，而基础知识一带而过的讲解模式，使学生不能很好地理解和接受所学内容，出现越拉越多、越来越难、越学越吃力的现象.

（三）学习气氛不浓，兴趣低、效率差.

医学院校《高等数学》课程学习气氛不浓，学生学习兴趣低、效率差，学生对《高等数学》课程学习状况不理想已成为一个“老大难”问题[5].主要原因表现为：

1.课程本身内容比较抽象，理论性较强，学生不愿意花费时间和精力学习，课下也很少进行相应的预习和复习，更有甚者作业中时常会出现抄袭现象.

2.部分学生未能正确认识《高等数学》课程的基础性作用，认为学习该门课程对自身的专业素质培养和提高没有作用或作用很小，因此轻视该门课程的学习.

3.许多学生进入大学后，兴趣部分转移到参加各种社团活动上，这大大挤占了其学习时间，特别是《高等数学》等基础通识类课程的学习时间.

三、数形结合法在《高等数学》教学中的应用实例

积分是《高等数学》中很重要的一部分内容，它和导数之间是互逆的关系.导数在中学的时候学生已经接触过，有了一定的基础，对学生来说这部分内容不是很难理解.但积分是导数的相反过程，往往逆向思维是比较困难的.因此，学生在学习积分部分内容时感觉比较吃力、难理解.在实际教学中，利用“数形结合法”对积分的相关内容进行讲解，取得了良好的教学效果.具体应用举例如下.

（一）积分上限函数教学应用案例.

牛顿（Newton）-莱布尼茨（Leibniz）公式是微积分基本公式，这个公式进一步揭示了定积分与被积函数的原函数或不定积分之间的联系[6].该公式以一个定理的形式给出，在讲这个定理之前，引入了一个非常重要的概念——积分上限函数，该定义对学生来说是个难点内容.

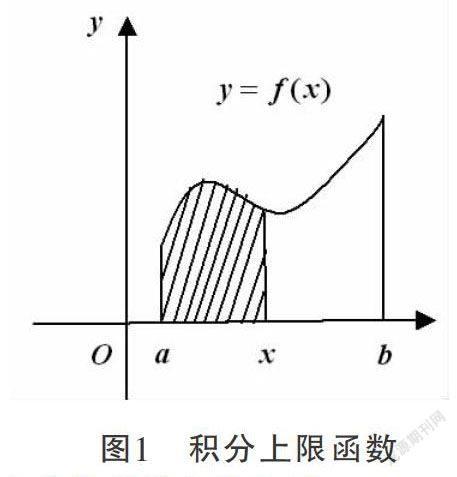
由于积分上限函数的定义中有定积分的式子，加之定积分本身就是一个比较抽象的概念，因此学生在理解积分上限函数时存在一定的难度.如果借助于几何图形，则由定积分的几何意义可知：定积分中如果被积函数f（x）≥0，定积分指的是以f（x）为曲边的曲边梯形的面积；如果被积函数f（x）≤0，定积分指的是以f（x）为曲边的曲边梯形面积的相反数.假设积分上限函数中的被积函数f（t）>0，积分上限函数表示的就是图中阴影部分的面积，如图1所示，随着x在区间[a，b]上变动，所对应的阴影部分的图形也在变化，其图形的面积也在不断变动，所以积分上限函数定义的是一个关于x的函数.对于被积函数f（t）<0的情况类似可得.这样利用“数形结合法”把抽象的数学式子用直观的几何图形表示出来，使学生能够很容易地理解和掌握该概念所表述的内涵，加深其学习印象.

（二）定积分计算教学应用案例.

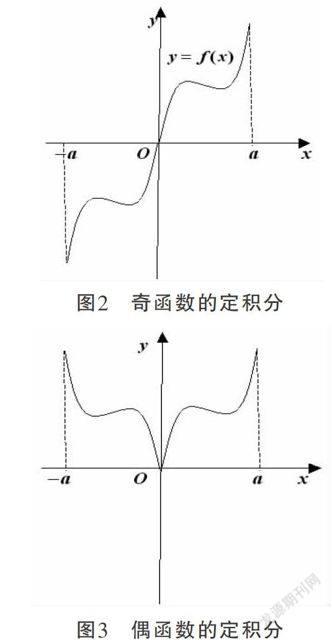
根据定积分的几何意义，可以得到定积分关于积分区间对称的性质：即当积分区间关于原点对称，被积函数为奇函数时，定积分等于0，被积函数为偶函数时，定积分等于一半区间上的两倍，如图2-3所示.通过图形可以使学生一目了然，看到该性质的正确性.

利用该性质，结合“数形结合法”，可以使一些复杂的定积分计算问题变得清晰、简单，具体如例1所述.

分析：本题的被积函数不是初等函数，因此在解题过程中尝试利用原函数求其定积分比较困难，并且该函数又不具有换元法和分部积分法所适用的被积函数的特点，所以利用一般的求定积分的方法也不易求得.但我们可以发现其积分区间是关于原点对称的，这时就需要考虑被积函数的奇偶性，但此被积函数本身并不具奇偶性.我们通过拆项发现，该被积函数可以拆成一个奇函数和一个偶函数，由此就可利用此性质简化积分运算.

四、结语

如上所述，在《高等数学》的教学实践中，融入“数形结合”教学法，将图形生动形象地展示在学生面前，有助于激发学生的学习兴趣.多媒体技术大大丰富了“数形结合”教学法在实际教学中的应用模式，对提高《高等数学》课程的教学质量，改善教学效果，提升医学生的专业素养和实践水平具有一定的积极作用，并可巩固《高等数学》课程在医学院校课程中的基础性地位.

参考文献：

[1]孔扬.医用高等数学教学实践与认识[J].科技资讯，2006（7）：163.

[2]张玉.对医学高职院校高等数学教学现状的思考与建议[J].卫生职业教育，2011（23）：56-57.

[3]鲍培文.例析数形结合思想在高等数学教学中的应用.当代教育理论与实践[J].当代教育理论与实践，2012（4）10：74-77.

[4]朱连宏，田丽，邹进.《高等数学》教学内容及教学方法的改革与研究[J].南昌教育学院学报，2010（25）2：130-131.

[5]葛家麒，董刚，杨宁，裴巍，郝虎建.独立学院高等数学课程教学内容与课程体系整体优化的研究与实践[J].东北农业大学学报，2010（8）1：57-60.

[6]同济大学数学系.高等数学[M].高等教育出版社，2007.