数形结合 画出数感 重在综合
徐黎明
“综合与实践”作为《义务教育数学课程标准(2011年版)》(以下简称《课程标准》)规定的四大课程内容之一,理应引起密切关注,扎实实施。《课程标准》指出:“综合与实践”的实施是以问题为载体、以学生自主参与为主的学习活动。它有别于学习具体知识的探索活动,更有别于课堂上教师的直接讲授。它是教师通过问题引领学生全程参与实践过程并相对完整的学习活动。那么,如何践行《课程标准》理念,扎实上好数学综合实践课?在“千课万人”活动中,笔者有幸聆听了特级教师华应龙老师的数学综合实践课“台湾长什么样”,现整理课堂实录,与同行共享。
一、引出问题,激发实践需要
(课件展示台湾风光图片:台湾故宫、镇宫大白菜、101大楼、阿里山、日月潭)
师:没有去过台湾的同学请举手。
师:想去吗?我刚刚去过台湾,去之前我到新华书店买了本书《畅游台湾》 ,里面这样介绍台湾。(课件出示:台湾本岛南北纵长395千米,东西宽度最大144千米,海岸线长约1139千米)看了这段文字你想到了什么问题?
生1:台湾有多大?
生2:台湾是什么形状?
生3:台湾这么辽阔,人口可以住多少?
师:是呀,我们可以提出很多问题,刚才有同学提出台湾长什么样?(板书)就看这三个数据,你能不能说一说台湾长什么样子?
生:我觉得台湾有可能特别长,因为南北纵长有395千米,东西宽度最大只有144千米,长长瘦瘦的,像一条带子一样。
师:嗯,肯定不是圆,如果是圆,南北长东西宽应该一样。你还能想到什么?
生:我觉得应该是椭圆形的。
师:能不能用这三个数据来说明。还是觉着这数据不够明确,怎么去处理,有些困难?这三个数据是395千米、144千米和1139千米【板书:(400+150)×2=1100(千米)】。这是我当时看到这三个数据后,写下来的式子。你看了这个式子有什么想法?
生:因为纵长395千米和宽度144千米,好像是在求长方形的周长。
师:哦!长加宽的和乘2,想一想,台湾可能长什么样?
生:长方形。
师:在这一式子里,我们把395看成400,把144看作150,这样估算出来的1100千米应该比台湾实际的周长要……
生:要多了。
师:对!台湾的海岸线实际上就是它的周长。
师:现在你再来说说台湾长什么样?
生:我觉着台湾它不是一个规则的图形。只是在原来长方形的基础上多一些。
生:它可能不是一个规则的长方形。
师:它不是一个规则的长方形。
生:多一些坑坑洼洼,弯弯曲曲。
【赏析】对于台湾,绝大部分学生听说过甚至去过,但对于台湾岛的形状却都不太清楚。华老师恰当选择有关台湾的风光图片和数据,引导学生提出了“台湾有多大?”“台湾是什么形状?”“台湾这么辽阔,人口可以住多少?”等问题,让问题生成于学习材料,有效地激发了学生的探究需求,学生有了“长长瘦瘦的,像一条带子一样。”“ 是椭圆形的。”“不是一个规则的长方形。”“(周边)多一些坑坑洼洼,弯弯曲曲”等初步感觉。在此也综合运用了周长的知识和估算的技能,迈出了数形结合的第一步,可谓是亮点初闪。
二、四画台湾,实现数形结合
(一)一画台湾,初成雏形
师:如果我们要画一个台湾长什么样?你想怎么画?
生:先画一个长方形。
师:画多大的一个长方形?长画4厘米宽画1.5厘米,或者长画8厘米宽画3厘米。想一想,你想怎么画。
师:现在请四人小组交流一下,说说自己是怎么想的。
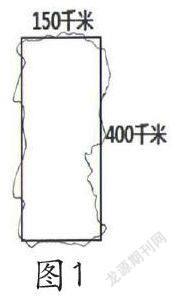
师:下面请金昊辰同学展示自己的作品。(见图1)
生:我觉着这个图形非常不规则。
师:还有其他意见吗?
生:我觉得台湾长得就这样。因为不是比长方形的周长还多了一些吗?
生:我觉得他画错了,宽度144千米,说明不应超过150千米。
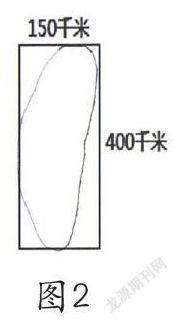
师:刚才我们六(5)班同学评价同学作品的时候非常好。先肯定作品的优点,再指出他的不足之处。下面我们请方格同学来展示自己的作品,哪位同学来评价这幅作品?(见图2)
生:感觉这样的弯曲比原来的还要短,
师:为什么说短了?能不能用学过的知识来解释一下?
生:因为斜的边比这两条边要短些。
师:为什么说短了?
生:因为斜边的边应该比这两条线要短些。
师:这好像是没学过数学的人讲的话。
生:以前学过,现在忘了。
师:哈哈!非常诚实的孩子。谁能帮她解释?
生:实际周长要比长方形周长长,而椭圆的周长要比长方形周长短,椭圆应该有许多弯曲,所以不对。
师:你说得很对,但是你没有回答刚才男生的话题,为什么弯曲的一定要比两条边短些?
生:其实我原先想改的,但是黑笔改不了。就拿这条斜边来说,可以把它看成一个近似的直角三角形,而直角三角形的两条直角边的长度要大于斜边的长度,所以长方形的周长要大于椭圆的周长。(掌声响起)
师:孩子们,你们慢了,掌声早该响起,人家方格同学自己画的,自己反思。刚才她用上了我们学过的什么知识?
生:三角形的两边之和大于第三边。
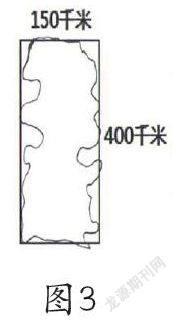
师:下面请周亦飏展示作品(见图3),看了周亦飏的作品你有什么感受?
生:有点长了。
师:先别说人家不好的地方,说说好的。你看作品南北纵长,东西宽度都符合要求,她画的海岸线长度肯定要比长方形周长长,不过是不是太长了些。孩子们,通过刚才这么一交流,我们要在长方形中画出台湾什么样子也不是件容易的事,可不是随便画的,应该有思考。画的时候必须注意什么?
生:南北、东西线不能超出长方形。
生:台湾的弧线不能太多,也不能太少,要控制好。
(二)二画台湾,画出数感
师:好!现在就请你在第2个长方形中,再画一个台湾的样子,这次争取能把你对数的感觉画出来。
学生尝试画图,同桌交流后集中反馈。
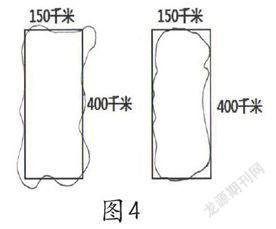
师:下面请朱晨乐同学来展示作品(见图4),现在看了她的作品,我觉得不能只看一幅,应该先看刚开始的一幅,再看现在画的一幅,觉得怎么样?
生:有进步!
师:对,老师也觉得进步很明显,刚刚我们展示的一些不完善的作品,其实每一个不完善的作品都是一个提示或指引,让我们前进一步。刚才有同学问台湾的面积多大(课件出示:面积约为3.6万平方千米),看完这条信息,你想到什么?
师:有同学在说400×150=60000平方千米(板书)刚才台湾的面积是多少?(3.6万平方千米)而我们算出来是6万平方千米,你想到了什么?
生:台湾有很多地方不是凸出来的而是凹进去的。
师:是不是这么一想,台湾原来长得很瘦小,不是很饱满。台湾的面积占长方形面积的几分之几?
生1:大约二分之一左右。
生2:五分之三。
(三)三画台湾,提高要求
师:对,或者说大约60%。是不是现在又想画了,琢磨一下怎么画,在第3个长方形中画出台湾的样子。
师:我发现有同学没有动笔,而是在思考,非常好。刚才我们有体验了,台湾的样子那不是随便就能画的。
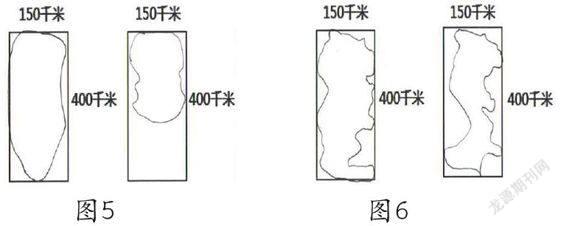
师:现在我们还是很期待着来欣赏同学们的作品,我们先来看金乐的作品(见图5),看了金乐的作品,有什么想说的?
生1:南北距离没到400千米,看起来面积像五分之三,但长度不够,画得不对。
生2:这椭圆的周长明显要比长方形小。
师:考虑周长短了,现在请金乐自己来说说,刚才你考虑了什么?没考虑什么?
生:我只考虑了面积,没有考虑周长和南北长度。
师:我们再来看看吴帆的作品。(见图6)
师:我知道你们笑什么了,是台湾长得吓人了。谁来评价吴帆同学的作品。
生:画得挺好的
师:是不是发现吴帆考虑挺周到的,考虑了好几个地方?
生:南北、东西长度,周长、面积都考虑了。
师:哎,我发现他南北还留了一点,挺细致的孩子。只是好像周长稍微长了些。
图5 图6
(四)四画台湾,接近真实
师:如果让同学们再画一个,这次你觉得要考虑哪些方面的问题?
学生第四次画台湾。
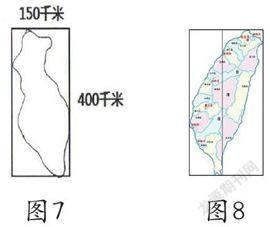
师:让我们再来看看吴帆同学的作品(见图7),感觉现在怎么样?南北?东西?周长?面积?想不想知道台湾究竟长什么样?
生:想。
师:(出示图8)是不是觉得很像?孩子们看着自己画的台湾的样子,然后比较台湾实际的样子。是不是有这样的感受:做事情往往不会一步到位,只要不断调整,就会走向完美。
图7 图8
【赏析】华老师在课上为学生提供简单又合适的学习材料——4厘米长、1.5厘米宽的长方形,让学生在长方形里面四画台湾岛,整个师生互动过程亮点纷呈。
一是学生尝试在先,展示师生评价在后。每一次画台湾,华老师总是让全体学生先在练习纸上,根据教师提供的信息、材料和前一阶段获得的阶段性成果尝试着画,并重点展示了7位学生真实的学习结果,让学生说出思考的过程,接着让学生相互评价、自我评价,学生有了自主实践过程的真实体验,能自然而然地说出对同伴或自己的作品的感觉,并不断地修正,使画出的图形越来越接近真实的台湾岛的样子,而教师则在一旁巧妙点拨。整个过程,恰到好处地体现了正确的师生观:学生是数学学习的主体,教师是学习的组织者、引导者和合作者。
二是教师逐步提高要求,提供必要数据,实现数形结合。二画台湾以后,华老师补充出示了台湾的面积,并提问“看完这条信息,你想到什么?”在有学生说出400×150=60000(平方千米)时,华老师又问:“刚才台湾的面积是多少?(3.6万平方千米)而我们算出来的是6万平方千米,你想到了什么?”在学生思维的关键节点上,教师总是不失时机地提问、追问和提供数学信息,提升了学生的思维水平,比较完满地体现了数形结合思想,提高学生综合应用数学知识的能力。
三是学生通过反思修正,台湾形状越来越逼真。在每一次学生画台湾后,华老师都会为学生提供自主反思的机会。如一画台湾后,华老师提出:“为什么弯曲的一定要比两条边短些?”在教师的问题引导下,学生自主整理、唤醒旧知,运用到了“直角三角形的两条直角边的长度要大于斜边的长度”的相关知识。又如二画台湾后,华老师运用对比,引导学生反思:“下面请朱晨乐同学来展示作品,现在看了她的作品,我觉得不能只看一幅,应该先看刚开始的一幅,再看现在画的一幅,觉得怎么样?”“现在请金乐自己来说说,刚才你考虑了什么?没考虑什么?”一个个问题,引导学生通过动手操作、纵横对比、评价修正,对台湾岛长什么样的概念由模糊逐渐清晰,数感——长方形周长、面积数据在具体情境中的感觉,也越来越明确,数学活动经验不断丰富,数学综合与实践课的特点随之凸显。
三、画后提炼,提炼思想方法
(多媒体讲述英国剑桥大学著名哲学家穆尔、罗素、维特根斯坦的小故事)
师:你能发现什么问题吗?
生1:考虑事情的时候要周到。
生2:做一切事情不可能一步到位。
生3:凡事都要递进,多考虑一些因素。
生4:不只是脑子里想,还要去实践。
师:是不是周长一定的情况下,面积可大可小?一个图形的周长、面积确定后,它的形状确定了吗?也就是根据刚才的四个数据,是不是一定能画出台湾的样子?
众生摇头。
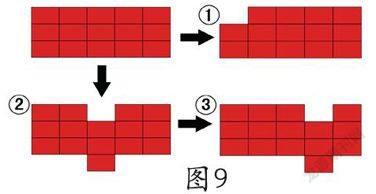
师:为什么?能不能举例子说一说?(课件出示图9)什么变了?什么没变?
生齐:(指①)面积变了,周长不变;(指②)面积不变,周长变了;(指③)面积一样,周长一样,形状不一样。
师:其实这种方法就是——举个反例。说明一个图形的面积和周长确定后,它的形状是不确定的,那也就是说,根据刚才的四个数据,是不是一定能够画出台湾的样子?
生:不一定。
师:对,只是可能画出台湾的样子。是不是还有其他问题?既然我们发现台湾长得什么样,台湾的面积不是长乘宽,那么台湾的面积又是怎么得到的呢?地球上的台湾又是怎么变成地图上的台湾的呢?是不是还有很多很多问题?送你一句话:发现问题即是收获。
【赏析】积累数学活动经验、培养学生应用意识和创新意识是数学课程的重要目标,应贯穿整个数学课程之中。“综合与实践”是实现这些目标的重要和有效的载体。在实施过程中,教师要注意观察、积累、分析、反思,使“综合与实践”的实施成为提高教师和学生素质的互动过程。华老师不是为了画台湾而画台湾,而是在学生四画台湾,积累了基本活动经验的基础上,引领学生通过倾听科学家的小故事、观察方格图周长、面积的变化等学习材料,把四画台湾的实践经历与感悟进行数学化抽象,及时提炼数学思想方法。由于教师的材料合适、点拨及时,学生果然有了“做一切事情不可能一步到位。”“不只是脑子里想,还要去实践。”等真实又贴切的感悟,学生的思考水到渠成、渐入佳境!华老师又以“发现问题即是收获”的经典语句结束全课,升华思想。
总之,华老师在教学设计和实施时特别关注了问题的选择、问题的展开过程、学生参与的方式、学生的合作交流,活动过程和结果的展示与评价,是一节“综合与实践”的样板课,值得我们为之喝彩并实践跟进。
(浙江省绍兴市上虞区小越镇中心小学 312367)

