为什么学生不想估，不会估？

焦肖燕 严育洪

【“望”：病例观察】

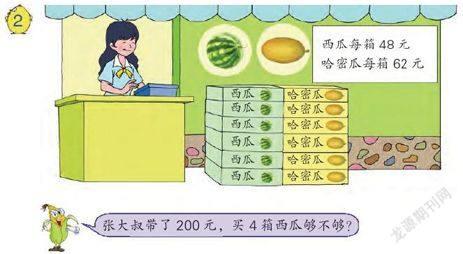
苏教版三年级上册《两、三位数乘一位数》单元中有一节估算课，教材例题是这样的——

这节课是在学生学习了整十、整百数乘一位数的口算后，让学生利用已学的乘法口算进行估算，解决实际问题。随着教学进程的不断推进，教师发现有些学生还是喜欢并坚持算出精确值：48×4=192（元），然后再与200元比较得到结果。有些学生虽然开始尝试用估算的方法，但总是不得要领，显得毫无章法，在要求他们有条理表述估的过程时，思维显得磕磕碰碰、处处卡壳。不过，经过教师的耐心讲解，学生在解答例题随后呈现的“300元够买5箱哈密瓜吗？”这一问题时，都能通过估算得到正确答案“不够”。

但在总结估算的好处时，却有一位学生发出了反对的声音：“不见得”。不由让人心生好奇。

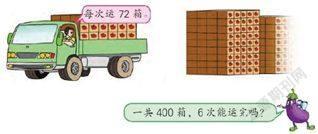
接下来，教学进入练习阶段，教师出示教材“想想做做”第6题——

一些学生能够把72看成70后进行估算，但最终的回答却是“不能”，让教师感到大惑不解。

【“问”：病历记录】

课后，教师把那个说“不见得”的学生和那些说“不能”的学生找来一问究竟——

首先问说“不见得”的学生：在解决“300元够买5箱哈密瓜吗？”这一问题时，把62看成60，60×5=300口算不是很容易吗？

生：老师，62×5我也能一下子算出结果，等于310。310>300。这样更容易。（顿了一下）有时用了估算反而容易做错。

原来如此！教师愕然……

再问那些说“不能”的学生：72×6>400，所以6次不是能运完吗？

生：嗯，现在我们想通了，6次能运完。没想到估算蛮难的。

师：那当时你们是怎么想的呢？

生：例题中62×5>300，带300元不够，现在72×6>400，我就想到6次不能运完。

原来如此！教师恍然。

【“切”：病理诊治】

通过课堂观察和课后询问，我们发现估算无论在知识层面还是心理层面，对三年级学生来说并不容易，分析如下：

一是数据的简单让学生不想估算。虽然学生对两位数乘一位数还没有学过，但由于数据比较小，并且像62×5进位也不复杂，一些聪明的学生凭借直觉自悟到了口算方法，也可能有一些学生已经通过其他途径学会了口算或笔算，于是对部分学生来说也就没了估算的需求。

二是思维的复杂让学生不想估算。虽然估算时把原来的算式转化成了整十数乘一位数，计算简便了，但是随后学生却要经历几次有序的推理过程，才能比出比较量与标准量之间的大小。例如，在估算62×5时，学生的思维需要经历这样几次连续的“转弯”过程：因为60×5=300，又因为62>60估小了，所以62×5>60×5，最终推出62×5>300。其中，学生的思维对象首先要把62想成60，最后又要把60还原成62，在这样的不断变换中，很容易造成学生思维的混乱，顾此失彼而出错。有些学生尽管比出了大小，最后还不能根据实际情境作出正确判断。因为这要求学生具备一定的生活经验和分析能力才能根据估算的结果作出判断，这对三年级学生来说要求也很高。那位学生说“有时用了估算反而容易做错”，不无道理。

研究表明，一个优秀的估算者，思维要经历三个关键过程：一是“简约”，即在保持原问题结构不变的情况下，更改数据以产生一个容易心算的形式的过程;二是“转换”，即将问题的数学结构变为易于心算的形式。例如，把8946+7212+7841变为8000×3等;三是“补偿”，即调整在对问题进行重新表述和转换时所进行的数字变化。例如，根据“估大”“估小”的情况对估计答案进行“调整”或“补偿”。由此可见，估算的要求高于笔算。

可以说，“学生不想估”这种情况很大程度上是由“学生不会估”造成的，也就是说，有时候学生感情的“为难”源自于事情的“难为”。

三是解题的习惯让学生不想估算。平常学生已经习惯于精确计算，答案是唯一的，学生的认识是非标准答案的得数都是错误的。而估算答案的不唯一，冲击了学生原本的计算习惯，也让学生心里感到不踏实。要估算134×4，一般把134看作100得到估算值400，例如“码头有400箱大豆，卡车每次能运134箱，4次能运完吗？”有时根据实际需要却要将134看作130得到估算值520，例如“码头有500箱大豆，卡车每次能运134箱，4次能运完吗？”至于什么时候需要接近精确值，什么时候可以与精确值拉开一定的距离，需要学生根据实际情境加以灵活判断，这样的“不定性”常常让学生“不定心”。于是，一些学生想到了“与其犹豫不决，还不如下定决心求出精确值”这一万全之策，以“不变”应“万变”。

然而，教师不能因为学生的不想估、不会估而使估算教学止步或走过场。估算是解决问题的有效策略之一，在实际生活中应用也非常广泛。一个人估算能力的强弱直接影响到人的生活节奏的快慢和工作效率的高低。由此可见，估算在数学教学中有着不可替代的教育价值：有利于培养学生对事物的直观判断力。同时，估算不仅能够很好地培养学生的数感，而且对培养逻辑推理能力也有很大的帮助。

估算应该从“小”（从小学生、从小细节）培养，针对上述课例中的问题，教师的积极态度应该是，基于学生的学习现状及思维难处，思考如何改进估算教学，而让学生不再只是“顾算”。对此，我们提出如下“分”与“合”的教学建议。

一、把知识难点“分一分”，让学生想估、会估

第一学段学生的估算意识和估算技术还处在形成过程中，教学不能一步登天，要善于使用“慢镜头”。“慢镜头”中有一种技术是“分镜头”，我们可以设计一些铺垫题，帮助学生先掌握“简约”和“转换”两个前期估算技术，从而分散难点。

为了激发学生估算的意识，教师还要学会借力人普遍具有的偷懒心理，因为人的偷懒行为是创造的动力，通过发明新方法、新技术来减轻负担，提高成效。在面对较大数目计算并不需要得到精确结果时，学生的第一反应是估算要比笔算省时省力，此时偷懒心理就可能促使学生主动尝试估算。根据以上理论，教师不妨在例题教学之前设计如下比较大小的题目：

312×5○1500      689×4○2800

设计这样的题目，一个方面的好处是因为数据大，学生乍一看就感觉心烦，再一看发觉还不会口算，心理障碍与知识障碍迫使学生只能放弃精确计算的习惯动作而去另辟蹊径。此时，教师就可顺应学生的需求，稍加点拨——“整百数乘一位数，你会口算吗？”引导学生想到迂回战术，间接地解决问题，以此掀开估算的盖头。开始时，学生或许有一种被逼的感觉（在此教师可以趁机让学生体会估算的必要性），但一旦领略到了估算的好处之后（在此教师可以趁机让学生体会估算的优越性），学生自然会对估算产生好感，从而重视估算在解决问题中的作用，进而迫切地想掌握估算技术——“何时用估算”“怎样来估算”“估算后怎么办”。当知识有了需求之后，知识之芯就能够与学生之心实现自然而有效的对接，很好地从“自上而下”的“教—学”形态转变为“自下而上”的“学—教”形态，估算教学也就能够水到渠成。

设计这样的题目，另一个方面的好处是有利于帮助学生一门心思地掌握估算的专项技术。虽然课程标准指出要“结合具体情境进行估算”，但对于第一学段的学生来说，估算涉及的思维过程相对复杂，所以在涉足实际问题的具体情境之前，先进行纯算式的比较，可以减少实际情境的干扰，降低学生的思维难度，使估算教学能够循序渐进。在这里，教师要重点引导学生掌握两种估算技能：一种是“小估”。例如把312看作300，300×5=1500，所以312×5>1500;另一种是“大估”。例如把689看作700，700×4=2800，所以689×4<2800。

在反馈时，教师应要求学生能够有序表达，在表达中让学生逐步体会估算技术：“一算”，算什么？口算整十、整百数乘一位数;“二比”，谁和谁比？要把实际的算式与标准进行比，而不是把算出的结果与标准比。

另外，教师应该引导学生学会灵活运用估算方法。例如757-349，如果把757看成整百数应该是800，349应该看作300，这样的结果是500，再看757中的57接近50，349中的49也接近50，则把这两个数分别看成750-350，结果是400，要比500更接近正确得数。

二、与生活经验“合一合”，让学生想估、会估

估算毕竟是一种开放性、创造性的活动，估算的方法不仅灵活多样，而且判断结果要根据实际情境来决定，往往有很多不确定的因素，因此当学生熟练掌握了估算技术的“一算”“二比”之后，接下来如何帮助学生根据实际情况，运用估算的结果来作出正确判断呢？教师应该创设更多的机会，让学生更多地接触现实生活中不同领域的数学问题，并能接触到各种不同的表述方式，培养学生具体问题具体分析的能力。

例如教师可以设计题组练习：（1）甲要打一篇400字的文章，平均每分钟可打53个字，8分钟能打完吗？如果把53看成50，因为50×8=400， 53×8>400，所以结论是“能”;（2）乙要打一篇400字的文章，平均每分钟可打48个字，8分钟能打完吗？如果把48看成50，50×8=400，48×8<400，所以结论是“不能”。这样强有力的对比，足以让学生意识到用估算解决实际问题不仅要会“算”，而且要会“比”，更要会“判断”。

又如在学习了两、三位数乘一位数后，出现这样一道练习题：“上午有3批学生来参观，每批69人，下午来参观的学生有213人，是上午参观的学生多，还是下午参观的学生多？”有估算意识的教师就不会简单地把它作为两位数乘一位数的复习题一带而过，而会充分利用这一素材，让学生运用不同的方法自主进行比较，对于想到用估算的方法来解决问题的学生给予表扬。

在随后的知识教学中，我们应该时时处处想到估算教学，只有在一段时间内不断进行估算训练（其中有一种常用方法就是把估算与笔算结合在一起，笔算前先估一估，以此作为验算的一种辅助方法），才能让学生对估算留下深刻的印象并熟练掌握估算技能，逐步形成估算习惯。

如在后续教学中，教师可以设计这样的题目：“博物馆门票每张8元，34个同学参观。带350元够了吗？”学生可能有这样几种估算方法：（1）34×10=340;（2）30×8=240;（3）30×10=300。教师对此可以问：“这些不同的估法，哪种最有说服力？”让学生认识到，其中第（1）种方法是往大估的，往大估也够，实际一定够，可以看出这种方法优于其他两种。教师接着还可以问：“哪种估法更接近精确值？”让学生认识到，其中第（3）种方法结果更接近精确值。教师之后不妨把题目改成：“博物馆门票每张8元，34个同学参观。买门票一共需要多少钱？”让学生认识到，什么时候可以用估算，什么时候需要算出精确值。通过这个“同题异问”的对比练习，帮助学生能够灵活处理生活问题和灵活选择估算策略。

另外值得一提的是，如果出现像上述课例中那样的“未教先会”的学生，笔算出62×5的结果之后来判断，教师也不能断然否定，应该在肯定的同时引导这位学生根据题目的特点来尝试采用估算的方法解决问题。另外，我们还可以外力驱动，例如设法模拟生活中不方便用纸笔运算的场景，使学生惯用的笔算没有用武之地，此时学生只能选择估算。总之，对于学生估算意识和估算能力的培养仅靠一两节课的教学是远远不够的，教师首先应该自己要有估算的意识，不能因为估算在考试中不考而忽视，其次在教学中要抓住一切时机组织学生进行这方面的训练，并做到持之以恒。

（江苏省无锡市东林小学   214007 江苏省无锡市锡山教师进修学校   214101）