Sm、La掺杂TiAl结构和性能的第一性原理计算
秦永和,乔英杰1
(1.哈尔滨工程大学材料科学与工程学院,150001哈尔滨;2.中国电子科技集团公司第四十九研究所,150001哈尔滨)
Sm、La掺杂TiAl结构和性能的第一性原理计算
秦永和1,2,乔英杰1
(1.哈尔滨工程大学材料科学与工程学院,150001哈尔滨;2.中国电子科技集团公司第四十九研究所,150001哈尔滨)
为研究稀土元素掺杂对Ti-Al系金属室温延性的影响,基于密度泛函理论第一性原理,应用广义梯度近似(GGA)和局域密度近似(LDA)平面波超软赝势法,建立稀土元素Sm、La掺杂TiAl晶胞模型,运用Castep计算分析Sm、La两种稀土元素掺杂的TiAl结构,对本征TiAl和掺杂TiAl的结构及力学性质进行分析.结果表明:稀土元素Sm掺入TiAl后,TiAl的共价性增强、成键方向性增加、硬度提高、离子性下降、延性降低;稀土元素La掺入TiAl后,TiAl的共价性下降、成键方向性减弱、硬度下降、离子性增强、延性提高.稀土元素掺杂金属间化合物,可改善其力学性能.
第一性原理;金属间化合物;稀土元素;电子结构
Ti-Al系金属间化合物以其低密度、高强度、高熔点、高弹性模量、耐腐蚀和优良的高温抗蠕变性能等优点,成为航空航天、工业燃气轮机以及汽车工业中最具潜力的高温结构材料之一.
Ti-A1系金属间化合物主要存在 Ti3A1、TiAl、TiAl2、TiAl3几种基本结构.其中,TiAl2和TiAl3相对较脆[1],Ti3Al由于钛的百分含量太多,密度比TiAl重,且抗氧化性能差[2],故而密度低、强度高、高温性能好的TiAl是钛铝系金属间化合物的代表化合物,但其室温脆性极大的阻碍了发展[3-5].有关TiAl金属间化合物抗高温氧化性能、抗熔盐腐蚀性能有很多报道[6-7],但对如何提高其室温延性尚未见报道.近年来,稀土元素掺杂提高金属间化合物延展性引起了人们的注意[8-9].然而,稀土元素对TiAl的合金化作用的研究还停留在初级阶段,在TiAl中加入稀土的相互作用微观机制目前尚不清楚.本文通过基于密度泛函理论第一性原理,分别应用广义梯度近似(GGA)和局域密度近似(LDA)平面波超软赝势法,分别建立稀土元素Sm、La掺杂TiAl晶胞模型,通过计算模型结构、弹性及电子性质,从本质上揭示稀土元素与TiAl之间的微观作用机制,从而找到提高TiAl室温延展性的方法.
1 计算方法与模型
在计算晶胞模型的电子结构和弹性常数时,采用密度泛函理论的第一性原理方法,利用Materials Studio软件中的量子力学模块CASTEP程序包展开.本文中交换关联能泛函选用广义梯度近似 GGA中的Perdew-Burke-Ernzerhof形式,赝势取倒易空间表征中的PBE超软(ultrasoft)赝势.应用CASTEP程序包建立TiAl单晶胞模型,见图1,TiAl单晶胞具有L10型超点阵结构,空间群为四方晶系,晶格常数 a=b=0.399 nm,c= 0.407 nm,c/a约为1.02[10].Ti原子坐标为(0,0,0)、(0.5,0.5,0),Al原子坐标为(0,0.5,0.5).建立的掺杂元素的超晶胞模型,见图2.图2(a)中稀土元素M替换超胞芯位Al的位置,即构成超胞模型Ti8Al7M;利用同样的方法使稀土M替换芯位的Ti原子即构成超胞Ti7Al8M,见图2(b).

图1 TiAl晶体结构计算模型
为确定动能截断值和布里渊K点网格数,分别做了截断能测试曲线图,见图3,布里渊K点的测试曲线图,见图4.通过曲线的收敛情况及要求的精度,最终确定动能截断值为360 eV,布里渊K点按4×4×4划分网格.在进行各项计算之前都用Broyden-Fletcher-Goldfarb-Shanno方法对超胞进行了几何优化,以求得局域最稳定结构.自洽场计算(SCF)时应用Pulay密度混合法,体系每个原子总能量的收敛值取5.0×10-6eV,每个原子上的力要求<10-1eVnm-1,公差偏移5.0×10-5nm,应力偏差<10-1GPa.

图2 晶胞计算模型

图3 截断能测试曲线
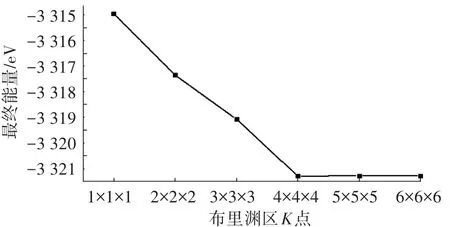
图4 布里渊K点测试曲线
3 计算结果与讨论
3.1 稀土元素在TiAl中占据位置判断
为研究确定稀土元素在TiAl中的占位情况,应用形成焓来判断稀土元素M在TiAl中较稳定位置的选择.位置选择能为

式中:E1、E2分别为Ti7Al8M和Ti8Al7M的形成焓.形成焓的定义为固态化合物和构成元素之间的总能量差异[11-12]为
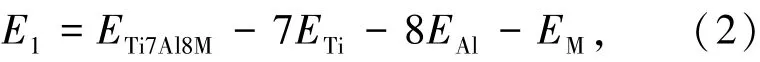

ETi、EAl和EM分别是纯Ti、Al及掺杂元素M在孤立状态的总能.故Esite可转变为如下形式:
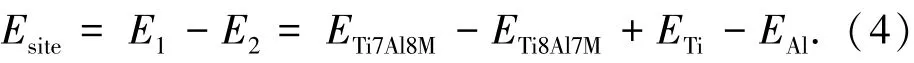
如果Esite<0,M倾向于占据芯位Ti的位置,如果Esite>0,M倾向于占据芯位Al的位置.对于面心立方的Al和Ti,其孤立时的能量分别为-5.235×103kJ/mol和-1.540×105kJ/mol,其模型构建方法为:建一个空间群,空间群符号与TiAl相同,晶格常数为 a=0.399 nm(a=b),c= 0.407 nm的单胞,Ti或Al原子坐标为(0.5,0.5,0.5),K点网格数为“gamma only”,晶格常数设为1 nm.

表1 Ti7Al8M模型和Ti8Al7M模型的总能量、位置选择能及所选位置
Ti7Al8M模型和Ti8Al7M模型的总能量以及各模型中掺杂元素的位置选择能见表1.从表中的Esite值表明Sm和La的位置选择能很强,倾向于占据Al的位置,所以相对较稳定的模型分别为Ti8Al7Sm模型、Ti8Al7La模型.
3.2 晶格常数
Sm、La掺杂前后TiAl晶格常数晶格常数及其变化 [δa=(a-0.399)/0.399,δc=(c-0.407)/0.407]见表2.由于稀土元素的掺入,使得模型的晶格常数不同程度增加.在这些模型中,Ti8Al7La模型的晶格常数变化比较明显,Ti8Al7Sm模型的晶格常数变化不大.
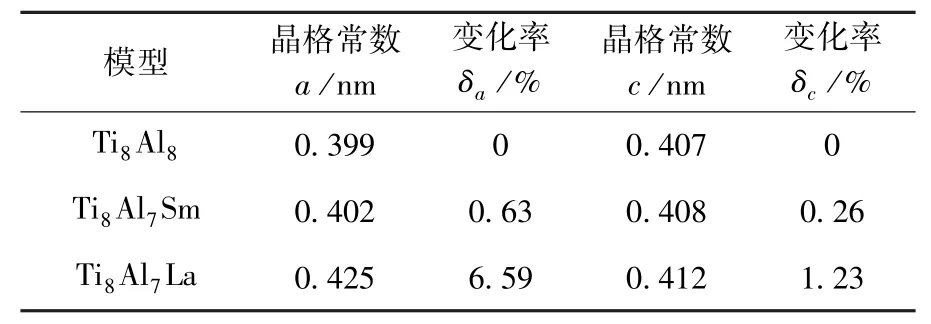
表2 Ti8Al7Sm及Ti8Al7La平衡时的晶格常数及其变化
3.3 弹性常数
一般的,材料的硬度与弹性模量有关,如杨氏模量E,剪切模量G.尽管对于不同的材料,其硬度与模量的关系有所不同,但是总的趋势是:模量越大,材料的硬度越大.因此,计算材料的杨氏模量和剪切模量可作为一种指导手段应用于材料的选择当中.体积模量B0可描述均质各向同性固体的弹性,可表示为单位面积的力,表示不可压缩性.G/B0为剪切模量与体模量的比值,被用于衡量材料的延性,Pugh提出可用G/B0来表征弹性模量与材料的弹性性质的关系,当G/B0<0.5时,材料具有延性;当G/B0>0.5时,材料表现为脆性.
泊松比v是材料横向应变与纵向应变的比值,也叫横向变形系数,它是反映材料横向变形的弹性常数.泊松比的范围是-1~0.5,泊松比的倒数1/v越小,材料的延性越好.
对于四方晶系,对照弹性模量矩阵方程,有C11、C12、C13、C33、C44、C66共6个独立分量,其力学稳定要求弹性常数必须满足如下条件[10]:根据四方结构晶体的弹性稳定性准则(C11-C12) >0,(C11+C33-2C13)>0,C11>0,C33>0,C44>0、C66> 0,(2C11+C33+2C12+4C13) >0;通过计算得到了各模型的弹性常数 C11、C12、C13、C33、C44、C66的值,见表3.计算所得的弹性常数都满足上式条件,表明这3种结构都是力学稳定的.对于正交(或四角)晶体,体模量和剪切模量的Voigt 和Reuss近似分别为
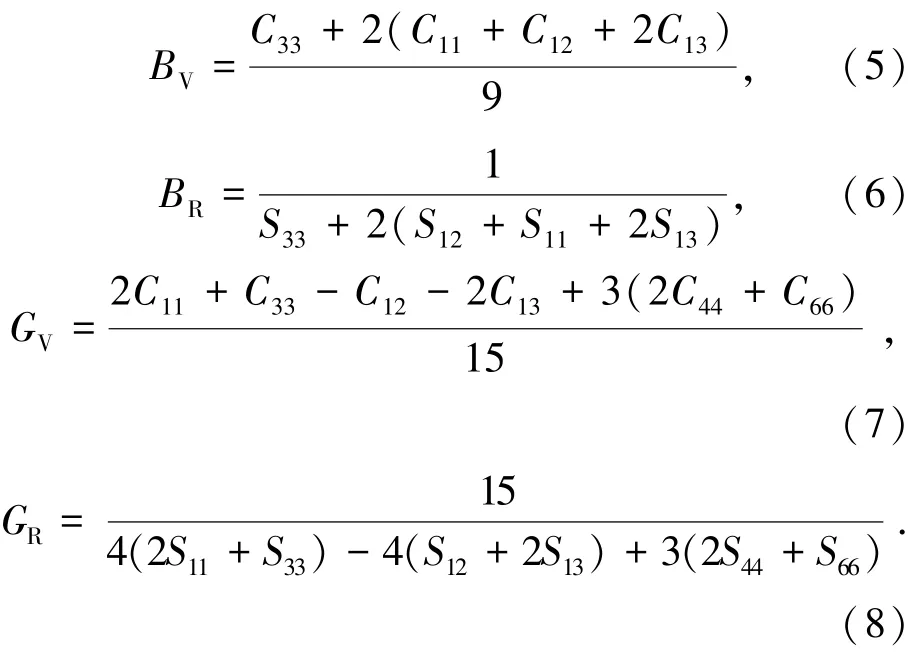
运用Hill经验平均计算体模量和剪切模量: BH=(BV+BR)/2、GH=(GV+GR)/2.杨氏模量E和泊松比v为

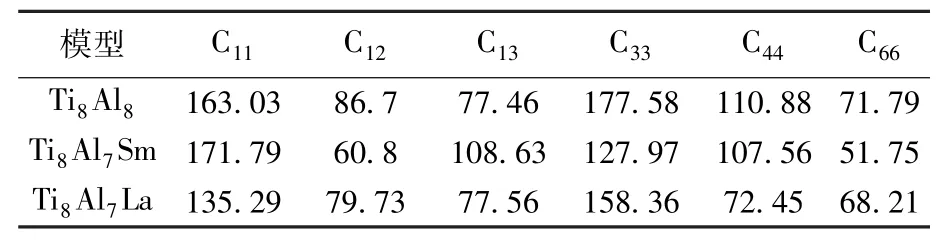
表3 各模型的弹性常数 GPa
通过式(5)~(10)得到表征各模型硬度和延性的参量,见图5.E和G表现出相同的变化趋势.稀土元素Sm的掺入提高了TiAl的硬度,稀土元素La加入降低TiAl的硬度.对于体模量B0,与Ti8Al8模型相比较,Ti8Al7Sm模型和Ti8Al7La模型均有所降低,即降低了TiAl的原子间结合能.G/B0的值越小,TiAl的延性越好.G/B0以及泊松比的倒数1/v表明稀土元素Sm掺入使TiAl的延性降低,而La则可提高TiAl的延性.
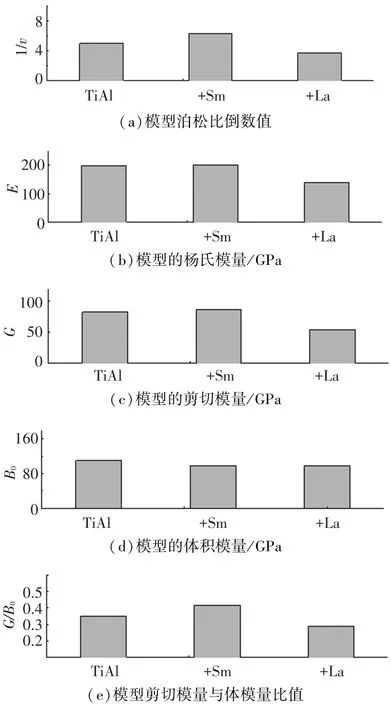
图5 TiAl、Ti8Al7Sm、Ti8Al7La模型的各模量值
3.4 电子结构
Ti8Al8模型的态密度见图6,可见Ti8Al8模型态密度的显著特征是在费米能级处,其尖峰主要是Ti原子d轨道电子的贡献,Ti和Al的相互作用主要是Ti的d电子轨道和Al的s、p电子轨道的杂化作用.
Ti8Al7La的态密度见图7.图中出现了两个尖峰,分别在-1.57×10 eV、-3.3×10 eV处,这是La 的s、p轨道与Ti的p轨道电子杂化作用的结果.La的掺入,降低了Ti d能态的峰高.

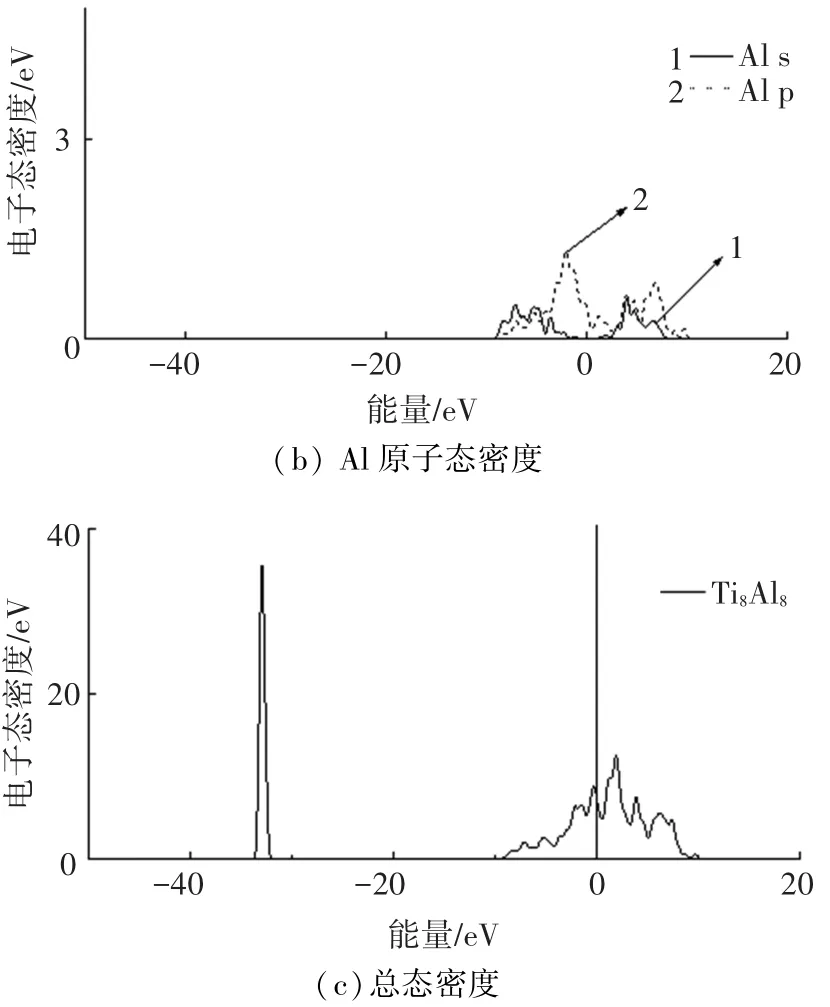
图6 Ti8Al8模型的分波态密度

图7 Ti8Al7La模型的分波态密度
Ti8Al7Sm模型的态密度图见图8,与Ti8Al8模型相比,Ti原子与Sm原子sp轨道杂化作用增强,Ti原子与Sm原子之间的成键作用增强.
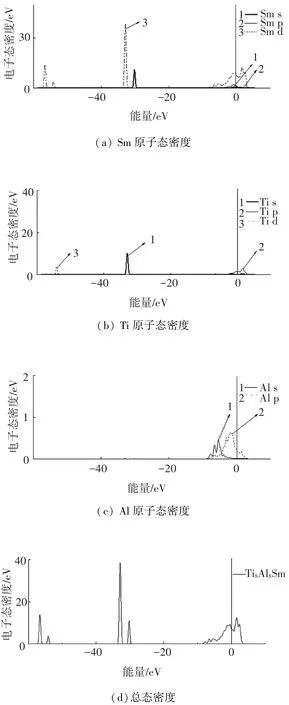
图8 Ti8Al7Sm模型的分波态密度
一般来讲,布居数是布居在不同能量层次的原子/分子的数量.键的布居表示的是两个成键原子电子云的重叠程度,可判断化学键的离子性与共价性[13-14].对于键的布居,最低值与最高值分别表示所成化学键的离子性与共价性的强弱.对于离子性和共价性,通过单位键长的布居得到的结果是相对的,共价键表征了电荷分布的方向性强,而离子键表征了原子间有电荷转移.当稀土元素替换了TiAl中的Ti原子或Al原子时,导致TiAl内部原子间的成键方式发生了改变,进而表现出宏观性质的差异性.
在Ti8Al8模型中,3种类型的Ti原子即可代表所有Ti原子位置的情况,即角位、棱位和面心位置.据计算结果可知,Ti-Al键的布居值均相同.Al-Al键(或Ti-Ti键)是由每一个Al原子(或Ti原子)与其最近邻的3个Ti原子(或Al原子)组成的,所有的Al-Al键(或Ti-Ti键)的布居值均相同.Ti8Al8模型各键的布居见表4.
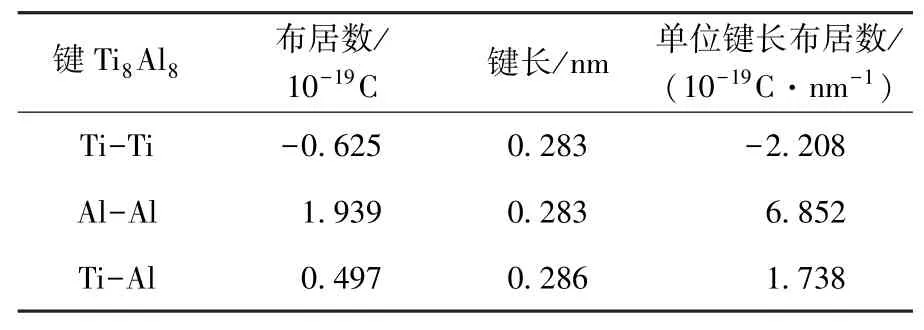
表4 Ti8Al8模型单位键长的布居
在稀土掺杂的模型中,根据表1计算可知,两种元素掺入Ti8Al8中,都占据Al的位置,即占据图2中Al1的位置.因为超胞的对称性,对于Ti-Al键,Al2与Ti1、Ti2、Ti4之间成键即表示所有Ti与Al成键情况,原子序号见图2.Ti8Al7La模型单位键长的布居见表5,与Ti8Al8模型单位键长的布居相比,对于Ti-Al键,部分单位键长布居数增大,表明Ti-Al键的共价性增强.Al-Al键单位键长布居数大幅减小,说明其共价性减弱.Ti8Al7La模型中不存在Al-La键.La只与Ti成键,且表现为极强的离子性.
Ti8Al7Sm模型单位键长的布居见表6,与Ti8Al8模型相比,对于Ti-Al键,单位键长布居数大幅增大,表明Ti-Al键的共价性增强;Ti-Ti键的布居值降低,说明他们之间的离子性减弱;对于Al-Al键,单位键长布居数减小,说明Sm的掺杂使其共价键减弱.Sm与Ti成离子键,Sm与Al成共价键.
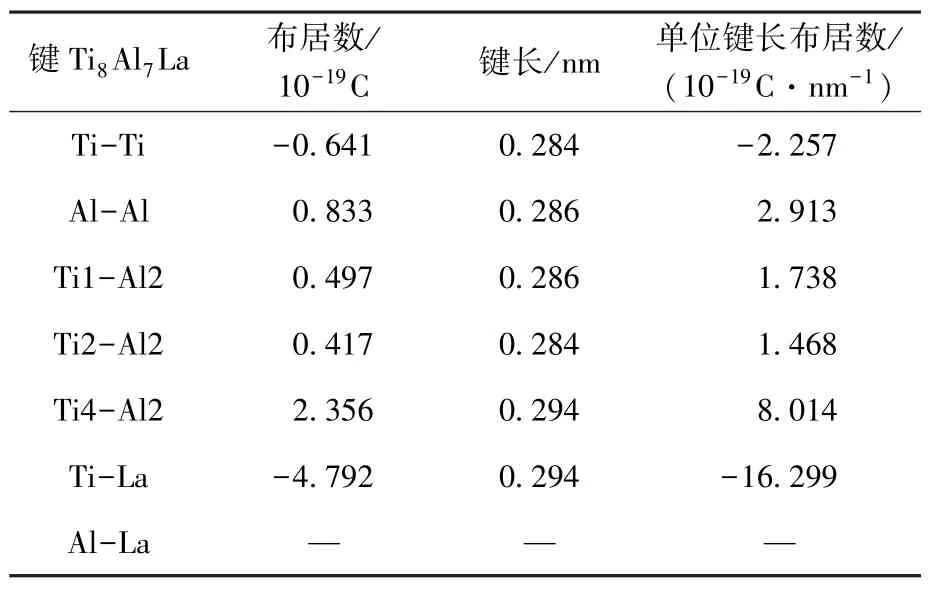
表5 Ti8Al7La模型单位键长的布居
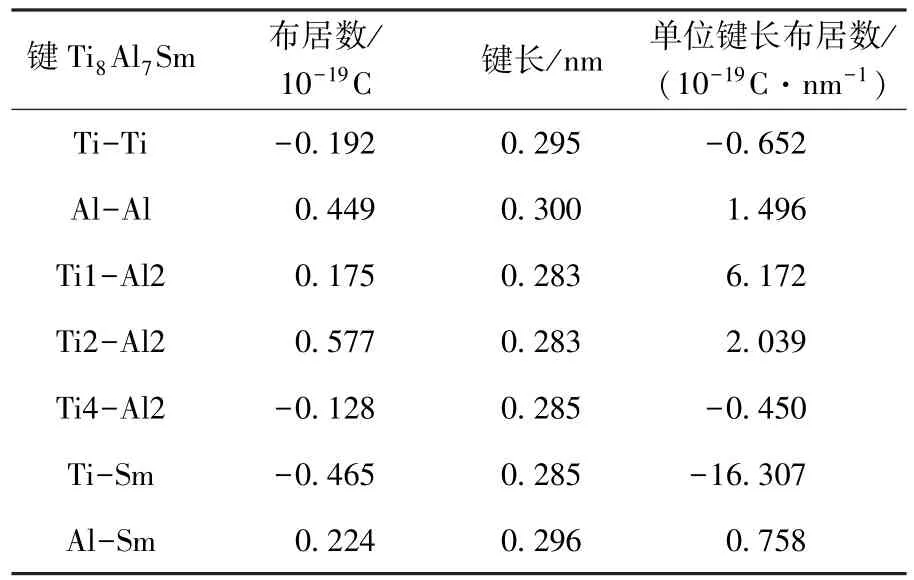
表6 Ti8Al7Sm模型单位键长的布居
将Ti8Al7La模型和Ti8Al7Sm模型布居数相对比发现,Ti8Al7Sm模型内部的共价性高于Ti8Al7La模型,离子性则相反.
综上所述,掺La的模型中,Ti与La的成键使模型中离子性增强,而Al与Al以及Ti与Ti之间反键作用使Ti8Al7La模型中共价性降低,方向性键的数量降低.因此Ti8Al7La延性较好而硬度较差.掺Sm的模型中,Ti-Al键的共价性增强、成键方向性增强,离子型降低.因而Ti8Al7Sm模型的延性降低而硬度提高.
4 结 论
1)稀土元素的掺入,使得模型的晶格常数不同程度增加.
2)稀土元素Sm掺入对TiAl影响如下:体模量B0有所提高,说明其原子间结合能降低;G/B0、泊松比的倒数1/ν均表明降低TiAl的延性;由态密度图和布居数分析表明其共价性增强,成键方向性增加、硬度提高.离子性下降,延性降低.
3)稀土元素La掺入对TiAl影响如下:体模量B0有所提高,说明其原子间结合能降低;G/B0、泊松比的倒数1/ν均表明提高TiAl的延性;由态密度图和布居数分析表明其共价性下降,成键方向性减弱、硬度下降;离子性所有增强、延性提高.
[1]徐福松,耿浩然,王守仁.镧对TiAl3金属间化合物显微组织及力学性能的影响[J].稀有金属材料与工程,2009,38(2):361-364.
[2]彭超群,黄伯云,贺跃辉.Ni-Al系、Fe-Al系和Ti3Al金属间化合物研究进展[J].特种铸造及有色合金,2001,6:27-29.
[3]李文,张瑞林.Ti-Al系的相图及金属间化合物[J].材料导报,1995,9(4):14-18.
[4] WANG Yan,LIU Yong,YANG Guangyu,et al.Microstructure of cast γ-TiAl based alloy solidified from β phase region[J].Transactions of Nonferrous Metals Society of China,2011(2):215-222.doi:10.1016/ S1003-6326(11)60702-4.
[5]吴建鹏,朱振峰,曹玉泉.金属间化合物的研究现状与发展[J].热加工工艺,2004(5):41-43.
[6] JIN Guangxi,QIAO Lijie,GAO Kewei.Effect of microstructure on hotcorrosion behavior ofTiAl intermetallics[J].Transactions of Nonferrous Metals Society of China,2004,14(2):210-215.
[7]彭小敏,夏长清,王志辉,等.TiAl基合金高温氧化及防护的研究进展[J].中国有色金属学报,2010,20 (6):1116-1130.
[8]QIU Congzhang,LIU Yong,HUANG Lan,et al.Effect of Fe and Mo additions on microstructure and mechanical properties of TiAl intermetallics[J].Transactions of Nonferrous Metals Society of China,2012,22(3):521-527.
[9]何君琦.稀土掺杂NiAl金属间化合物结构和性能的第一性原理研究[D].哈尔滨:哈尔滨工业大学,2013.
[10]陈国良.金属间化合物结构材料研究现状与发展[J].材料导报,2000,14(9):1-5.
[11]吴平伟,朱志斌,戴金辉.Amond软件在晶体对称性教学中的应用-32点群晶体模型库的建立[J].化学通报,2007(10):556-558.
[12]殷开梁,邹定辉,杨波,等.Materials Studio软件涉及力场中氢键的研究[J].计算机与应用化学,2006.23 (12):1335-1340.
[13]杜永胜.Materials Studio在固体物理教学中的应用[J].技术物理教学,2009,17(3):45-46.
[14]吴红丽,张伟,宫声凯.Nb元素影响Ti-Al金属间化合物键合特征的第一原理计算[J].化学学报,2008 (6):14-15.
(编辑 苗秀芝)
The first principle calculation for structure and mechanical property of Sm,La doping with TiAl
QIN Yonghe1,2,QIAO Yingjie1
(1.College of Materials and Chemical Engineering,Harbin Engineering University,150001 Harbin,China;2.The 49thResearch Institute,China Electronics Technology Group Corporation,150001 Harbin,China)
In order to research the influence of doping lanthanon on Ti-Al series ductility in room temperature,based on first-principles full potential linearized augmented plan wave method,we use generalized gradient approximation(GGA)and local density approximation(LDA)to build a unit cell model,and use Castep to calculate and analyze TiAl structure doped with Sm,La,structure and mechanical property of intrinsic TiAl and doped TiAl.The data show that as TiAl has been doped with Sm,covalency of TiAl is enhanced,bonding directivity and hardness are improved;ionicity is declined and ductility is reduced.As TiAl has been doped with La,covalency of TiAl is declined,bonding directivity and hardness are reduced;ionicity is enhanced and ductility is improved.Therefore,doping intermetallic compounds with lanthanon may improve mechanical property,it is a promising research direction.
the first principle;intermetallic compounds;lanthanon;electronic structure.
TB331
A
0367-6234(2015)05-0123-06
10.11918/j.issn.0367-6234.2015.05.021
2014-12-07.
电子信息产业发展基金(0602SK002).
秦永和(1972—),男,副教授,博士研究生;
乔英杰(1965—),男,教授,博士生导师.
乔英杰,qiaoyingjie@hrbeu.edu.cn.

