G.HN标准中十字星座QAM低复杂度解映射算法

徐 娟，姚如贵2，南花妮2，高凡琪2

（1.长安大学电控学院，710064西安；2.西北工业大学电子信息学院，710072西安）

G.HN标准中十字星座QAM低复杂度解映射算法

徐 娟1，姚如贵2，南花妮2，高凡琪2

（1.长安大学电控学院，710064西安；2.西北工业大学电子信息学院，710072西安）

为降低G.HN标准中十字星座QAM解映射的复杂度，首先引入对数似然比贡献权值，衡量参考星座点对解映射的贡献；提出十字星座QAM低复杂度解映射算法，搜索范围缩小为对数似然比贡献权值较大的参考星座点；讨论算法边界情况的搜索范围确定方法；研究信道估计辅助的自适应搜索范围选择方案.仿真结果表明，本文所提算法在获得与全搜索范围相同的误码性能前提下，减小平均搜索星座点数，2 048-QAM和512-QAM解映射平均搜索星座点数仅为全搜索范围的1.9%和5.7%.简化算法较好的平衡性能和解映射复杂度，具有较大的工程应用前景.

正交幅度调制（QAM）；十字星座；解映射；信道估计；搜索范围；贡献权值

2009年10月ITU-T Q4/SG15工作小组正式发布G.HN家用网络标准G.9960协议［1］，致力于下一代家用网络收发器能够在多种类型的家用线缆（包括电话线、电缆、电力线，以及它们的组合）上运行，支持高达1 Gbit/s的数据传输.为提供高速率的数据传输服务，协议采用OFDM调制方式，并且每一子载波采用高阶正交幅度调制QAM （quadrature amplitude modulation）.由于QAM具有高效的功率效率和带宽利用率，广泛应用于其他各种通信系统，包括数字电视广播［2］，宽带接入［3］等标准.

针对QAM的解映射算法，国内外学者展开了研究.文献［4］研究高阶QAM解调的Log-Map算法和简化Max-Log-Map算法，分析算法的复杂度，并通过仿真验证与3GPP Turbo码合作的性能.文献［5］根据BCJR算法［6］推导软解调的对数似然比计算公式，将方形QAM星座的解映射分解到I和Q路分别进行，有效的降低搜索范围.文献［7］提出一种折线逼近简化算法，基于曲线族的特点用简单的线性运算替代标准算法中复杂的非线性运算，复杂度有所降低.但是算法需要判断各比特的折变点，耗费较多资源和时间.而且，每一段逼近都存在误差，会降低系统的性能.文献［8］提出一种边界法的对数似然比LLR（loglikelihood ratio）简化算法，运算量较小，但误码性能不太理想.而且，高阶QAM的星座点数多，分界线也多，要确定相应的软信息计算公式很困难.上述文献均针对正方形星座QAM解映射算法研究.文献［9］推导G.HN中的正方形和十字星座QAM解调算法，但是解映射时，进行全集合搜索，由于未考虑高阶QAM的简化算法，工程实用困难.本文针对高阶十字星座QAM的解映射技术进行讨论，基于对数似然比贡献权值提出了一种低复杂度解映射算法，研究边界情况的处理方法，并利用信道估计辅助自适应选择搜索范围，在算法复杂度和性能之间达到良好平衡.

通常情况下，为提高系统性能，将信道编码与高阶调制进行联合设计.本文采用G.HN中QCLDPC码［1］，充分利用QAM解映射输出的软信息，信息比特长度为960，码率为1/2，译码算法采用Layered TDMP算法［10］，8次迭代，最大仿真帧数为106.

1 QAM调制、解映射

为讨论高阶QAM解映射算法，首先简单回顾十字星座QAM调制映射规则和软判决解映射技术.

1.1 QAM调制

本文仅研究十字形星座M-QAM（M=2m，m=5，7，9，…）.将星座点用复数对｛Ik，Qk｝为，每个点都对应m比特.具体映射步骤如下:

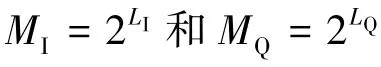
2）为增大汉明距离，一般采用Gray映射，将两组输入的Gray映射序列分别转换为自然二进制序列，第I组为BI=（b0，…，），第Q组为BQ=（bLI，…，bm-1）.具体转换规则为

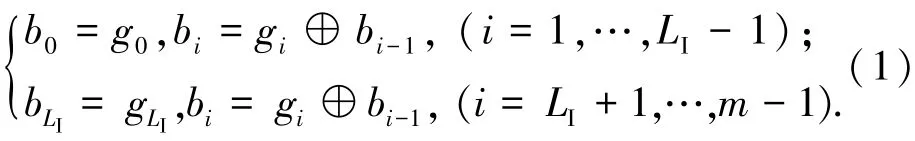
3）计算I、Q两组二进制序列对应的十进制数为

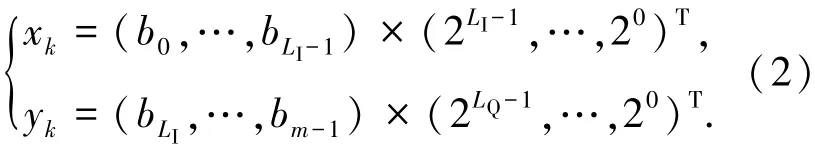
4）根据｛xk，yk｝计算归一化坐标为

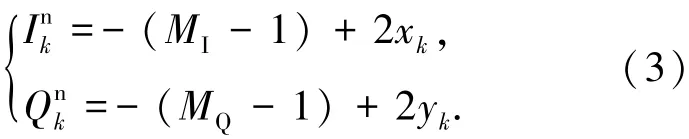
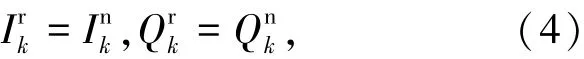
其中符号函数sign（x）定义为

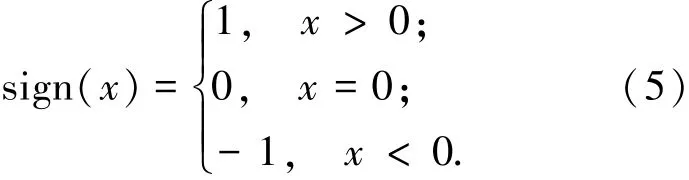
6）最终映射到星座点的坐标设为｛Ik，Qk｝，用复数表示为Ak=Ik+jQk，

式中χ（m）是功率归一化因子，与QAM的阶数M=2m有关的一个固定值［1］.

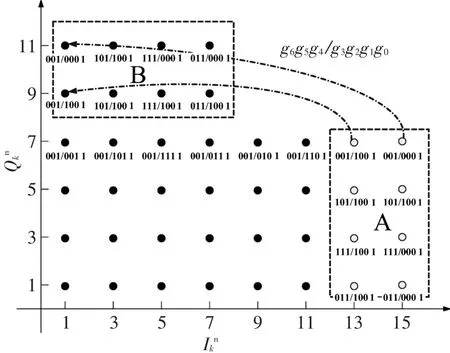
图1 128-QAM第一象限旋转过程示意

图2 128-QAM整体星座

1.2 QAM解映射

QAM解映射的任务是计算传输数据对应的信息，解映射的输出可以是硬判决数字比特，也可以是对发送端数字比特软判决的有效度量值［4-5，9，11］.一般软判决解映射与信道译码（如Turbo码［4］、LDPC码［5，9，11］等）联合设计，基于使信道噪声影响最小化的原则，进一步降低传输的误码率.

对QAM软判决解映射进行详细的说明.假设第k时刻接收信号rk为

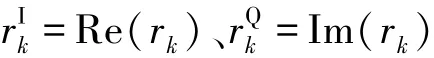
由于十字星座映射过程中I和Q分量之间有旋转操作，不能对I和Q分量分别进行解映射（如正方形星座［5］）.因此，只能根据BCJR算法推导出的对数似然比公式进行解映射.

在给出软判决计算公式之前，首先给出几个重要集合的定义.假设 M-QAM星座为 C= ｛c1，c2，…，cM｝.定义gi=1和gi=0（i=0，…，m-1）对应的星座点集合为C1（i）⊂C、C0（i）⊂C，各有M/2个星座点，且C1（i）∩C0（i）=Φ，C1（i）∪C0（i）=C.图3（a）～（e）示例了32-QAM星座点针对比特g0，…，g4的集合划分，实心圆和空心圆分别对应集合C1（i）和C0（i），i=0，…，4.

软判决解映射输出的是序列（g0，…，gm-1）对应的软信息Λ=（λ0，…，λm-1），其中λi定义为比特gi在接收到符号rk的对数似然比，计算方法为［5］

式中i=0，…，m-1.每个比特gi的对数似然比计算需要遍历C=C1（i）∪C0（i），共有M个星座点.解映射一个比特需要遍历M/log2M个星座点.例如，对于2 048-QAM，解映射一个比特，需要遍历2 048/log22 048≈186个星座点.显然，当QAM阶数很高时，解映射搜索星座点数很大，而且对数似然比的计算涉及平方-指数-求和运算，需要耗费大量的时间和硬件资源，很难应用于高速数据传输应用中.因此，有必要进一步降低解映射复杂度，拓展高阶十字星座QAM的实际应用前景.

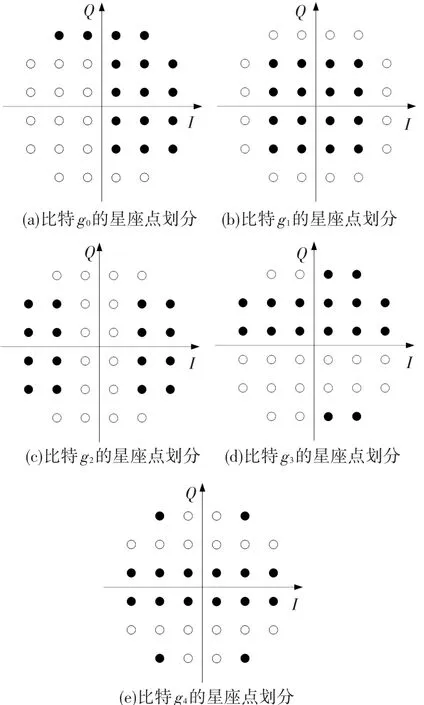
图3 星座点集合划分示例（32-QAM）

2 对数似然比贡献权值

由此，为缩小搜索范围，进而降低QAM解映射的复杂度，引入对数似然比贡献权值.

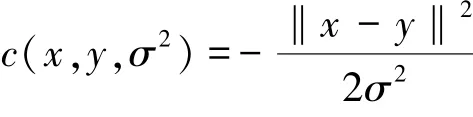
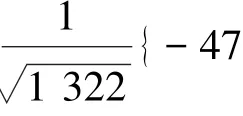
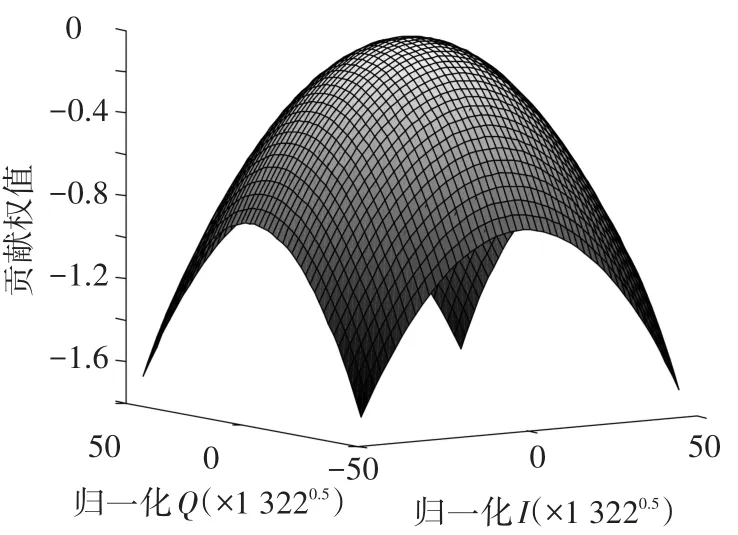
图4 不同参考星座点时对数似然比贡献权值比较（2 048-QAM，接收信号为0+j0，σ2=1）

由图4可知，给定σ2时，距离接收信号近的参考星座点对应的贡献权值较大，在计算对数似然比时贡献也大.随着接收信号和参考星座点的距离逐渐增大，贡献权值以O（x-2）速度降低.所以，计算对数似然比时，如果仅仅考虑部分贡献权值较大的参考星座点，可以缩小搜索范围，有效降低算法复杂度.

3 十字星座QAM低复杂度解映射算法

引入一个基本单位，定义为星座点间隔Δ，表示任意两星座点之间的最小距离.根据QAM调制，星座点间隔Δ=2χ（m）.后续讨论搜索范围时，均以JΔ的形式给出，其中，J为正整数，不引起歧义时简写为J.定义⊗为笛卡尔乘积，X⊗Y为和Q的取值范围分别为X和Y.

由第2节中关于贡献权值的讨论可知，距离接收信号较远的参考星座点对于对数似然比计算结果贡献很小，可以忽略.因此，在计算对数似然比时，仅考虑贡献权值较大的参考星座点.本文提出将解映射搜索范围限定在以接收信号为中心、距离接收信号为JΔ的正方形（正方形的边平行于I和Q轴）中，如图5所示的虚线框.

3.1 算法描述

3.1.1 搜索范围确定

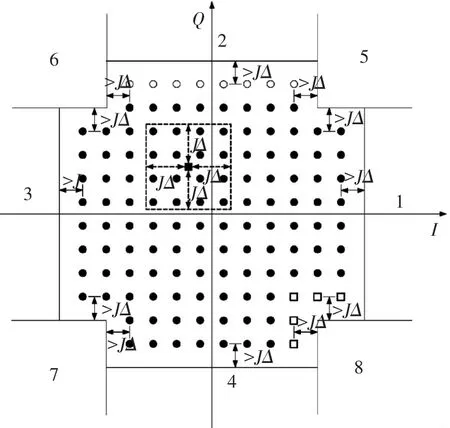
图5 接收符号相对于参考星座点的3种情况

表1 特殊区域搜索范围设置

3.1.2 对数似然比计算

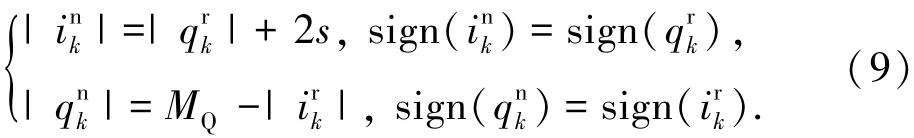
3）计算归一化坐标对应的十进制数为

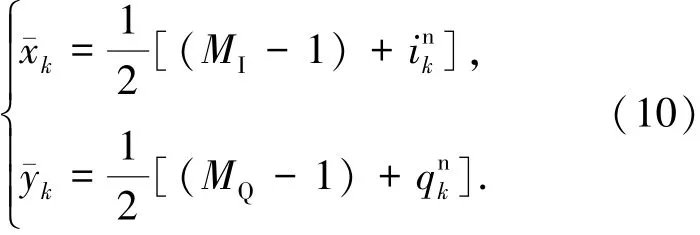
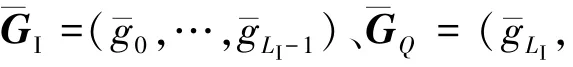
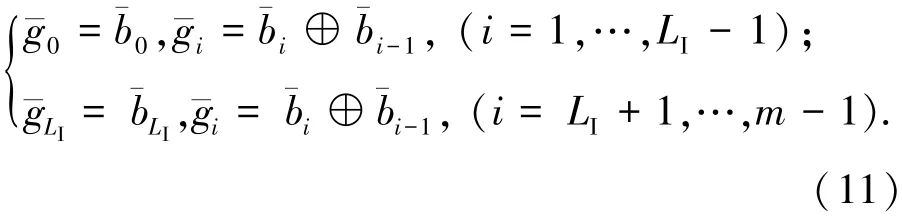
3.2 对于边界情况搜索范围的讨论

以下讨论均基于2 048-QAM（m=11），假设接收信号rk=Ak+nk，发射信号为Ak=χ（m）（Cmax+ j），即邻近图5中区域1的一个星座点；噪声方差为σ2，则nk～CN（0，σ2）.下面讨论给定发射信号Ak，且接收信号位于图5区域1的概率.为简化讨论，不考虑的影响.概率计算为式中erfc（x）为误差互补函数［12］.图6显示不同信噪比时接收信号位于图5区域1的概率.

由图6可看出，当发射信号位于星座图的边缘，且J选择较小时，即使信噪比较大（＞20 dB），接收信号位于特殊区域（如图5中区域1～8）的概率较大.当然，J取值较大相应概率较小，但是，此时解映射搜索范围较大，不利于降低复杂度.因此，对于接收信号位于特殊区域时的解映射需要进行特殊处理，搜索范围见表1.

图6 接收信号位于图5区域1的概率（2 048-QAM，Ak=χ（m）（Cmax+j））

3.3 关于搜索范围的讨论

确定搜索范围可有两种方式:固定搜索范围和信道估计辅助的搜索范围设定.

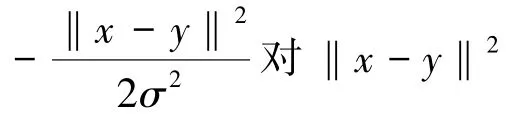
基于上述的分析结论，搜索范围可根据信道估计结果自适应设置.由于J和信噪比之间很难给出一个闭合的表达式，因此，工程上一般根据先验的信息进行设定.在给定信噪比RSN0条件下，根据仿真或者实测结果，选择测试BER与全集合测试BER的偏差较小时所对应的J0.在实际应用时，若信道估计为RSN0，则选择J0作为搜索范围.

图7 不同搜索范围和不同信噪比条件下BER性能对比

根据图7的仿真结果，表2、3给出不同信噪比条件下搜索范围设置.

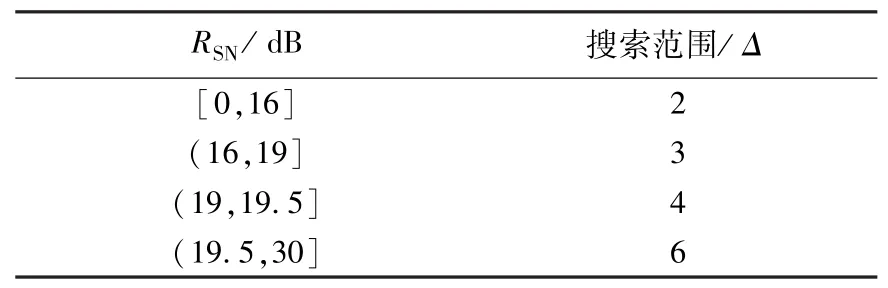
表2 512-QAM条件下不同信噪比对应搜索范围

表3 2048-QAM条件下不同信噪比对应搜索范围

由表2、3可看出，信噪比越大，搜索范围越大，与上述分析吻合.另外，由于调制阶数越高，相邻参考星座点之间的距离越小.因此，对于调制阶数高的解映射，需要设置更大的搜索范围，保证软判决贡献权值较大的参考星座点均能包含于搜索范围中.

3.4 复杂度分析

分析本文所提算法的时间和空间复杂度.其中，时间复杂度由搜索星座点数衡量.

给定搜索范围J，若不考虑边界情况，根据十字星座QAM低复杂度解映射算法描述，解调一个符号最多搜索（2J+1）×（2J+1）个星座点，当J取值较小时，（2J+1）2≪M（M为全集合搜索对应的搜索星座点数）.事实上，由于存在边界情况，解调一个符号平均搜索范围约为（J+1）2.

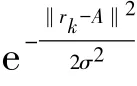
综上，由于采用本文算法可以有效缩小搜索范围，时间复杂度远远小于全集合搜索解映射算法.

4 仿真结果

本文所提G.HN标准中十字星座QAM低复杂度解映射算法的性能进行仿真，考核指标包括误比特率（BER）、误帧率（FER）和平均搜索星座点数.由于未检索到十字星座QAM低复杂度解映射算法相关研究结果，本节的性能及复杂度仅与原始未简化算法（即全集合搜索解映射算法［9］）进行比较.对于搜索范围的设定，本文所提算法采用表2、3的参考设置.

图8显示本文所提解映射算法的BER和FER性能.可看出，对于高阶十字星座QAM，本文所提算法均可以达到与全集合搜索相近的误码性能.

验证本文所提解映射算法复杂度，采用解映射时每比特平均搜索星座点数进行评估.设计如下试验:关注信噪比范围为［10，30］，步进为2 dB；针对每个信噪比，进行105帧的Monte Carlo仿真［13］，统计解映射时每比特平均搜索星座点数.仿真结果见图9和表4、5.

由图9可看出，不同信噪比条件下，搜索范围进行自适应调整，与表2、3设定值一致，但平均搜索星座点数远小于全集合 （以“□”标记）.表4、5给出在仿真信噪比范围内的平均搜索星座点数对比（第3行为平均搜索点数相对于全集合的百分比）.对于2 048-QAM，本文所提算法的平均搜索点数为3.49（仅占全搜索范围的1.9%），即可获得与全集合搜索相同的误码性能；虽然本文所提算法的平均搜索点数＞J=3、J=4对应的搜索范围，但是，综合图7、8，可看出，本文所提算法的BER和FER性能要优于这些搜索范围对应的性能，尤其在高信噪比（≥22 dB）条件下.对于512-QAM，可获得相同的结论.同时，由表4、5可计算，平均每个符号搜索星座点数约为（J+1）2，验证“3.4复杂度分析”一节的相关结论.例如，对于512-QAM和J=6，平均每个符号搜索星座点数约为5.06×log2512=46≈（6+1）2.

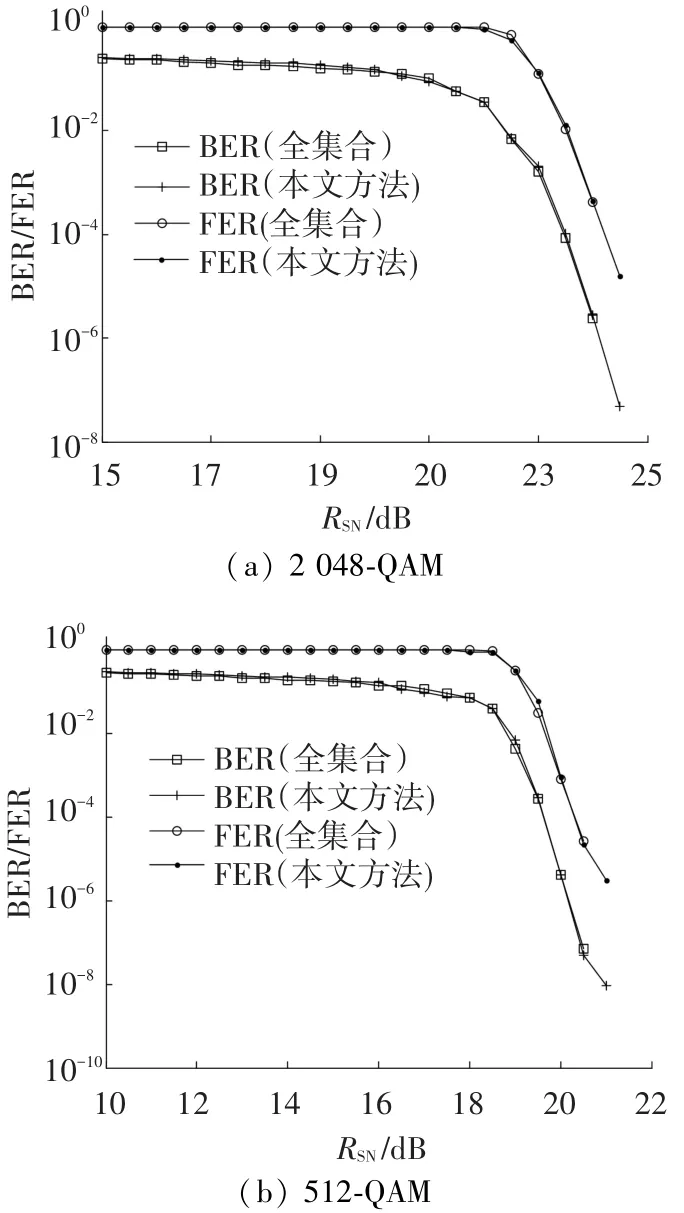
图8 本文所提解映射算法BER和FER性能比较

图9 不同信噪比条件下每比特搜索范围对比

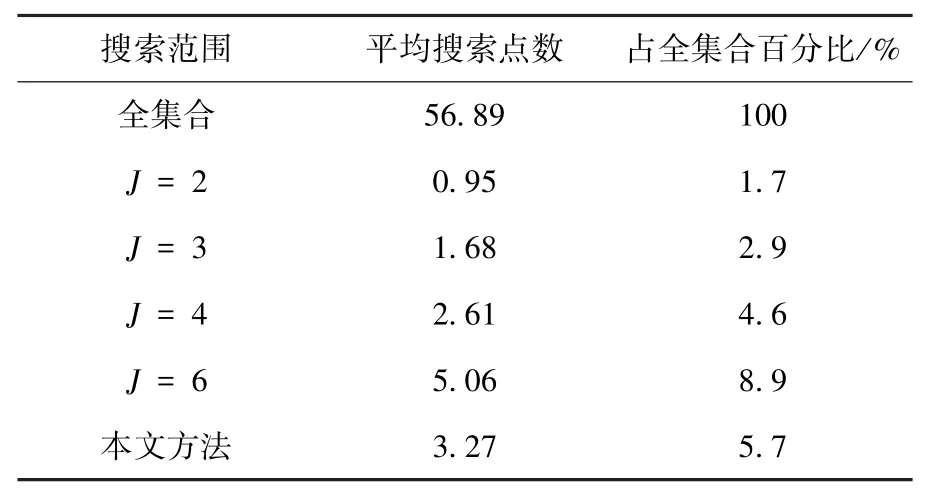
表4 512-QAM时每比特平均搜索星座点数对比（信噪比范围为［10，30］，步进为2 dB）

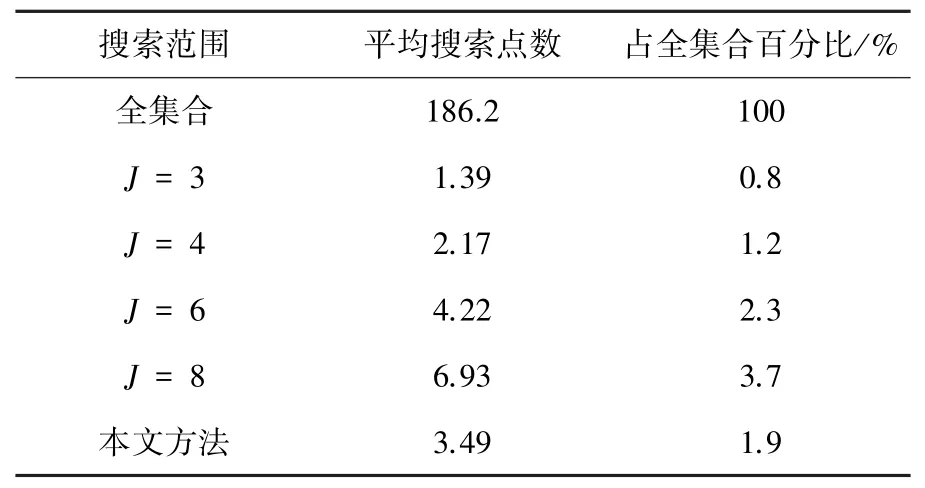
表5 2048-QAM时每比特平均搜索星座点数对比（信噪比范围为［10，30］，步进为2 dB）

5 结 语

G.HN标准中采用高功率效率和带宽利用率的QAM调制.但是，当QAM调制阶数较大，且采用软判决解映射时，搜索范围很大，需要消耗大量计算资源.对于十字星座QAM，由于I、Q之间存在旋转映射，解映射复杂度更高.针对这个问题，本文研究十字星座解映射对数似然比计算公式的特性，引入对数似然比贡献权值，用于衡量参考星座点对对数似然比的贡献，距离接收符号越近的参考星座点，贡献权值越大.基于此，提出十字星座QAM低复杂度解映射算法，搜索范围只包含贡献权值较大的参考星座点；讨论算法边界情况的搜索范围确定方法；并研究信道估计辅助的自适应搜索范围选择方案.仿真结果表明，本文所提算法在获得与全集合搜索范围相同的误码性能的前提下，大大减小平均搜索星座点数.若放松对误码性能的要求，搜索范围还可以进一步减小.本文所提算法较好的平衡性能和复杂度，具有较大的工程应用前景.

［1］ITU-T.Unified high-speed wire-line based home networking transceiver［S］.G.9960，October 2009.

［2］MCNS.Data-over-cable service interface specifications: Radio Frequency Interface Specification［S］.SP-RFI v2.0-105-040407，2004.

［3］Ki Hyuk Park，Dae Kyo Shin，et al.Design of a QPSK/ 16 QAM LMDS downstream receiver ASIC chip［C］// Proceedings of IEEE Workshop on Signal Processing Systems.Lafayette:IEEE，2000:210-217.

［4］何燕锋，杨鸿文，郭文彬.高阶调制的软输出算法比较［J］.北京邮电大学学报，2003，26（1）:82-85.

［5］何轶，姚如贵，王伶.M-QAM系统中QC-LDPC译码性能研究［J］.电子设计工程，2012，20（8）:136-138.

［6］BAHL L，COCKE J，JELINEK F，et al.Optimal decoding of linear codes for minimizing symbol error rate ［J］.IEEE Transactions on Information Theory，1974，20（2）:284-287.

［7］闫涛，茹乐，杜兴民.一种基于折线逼近的对数似然比简化算法 ［J］.电子与信息学报，2008，30（8）: 1832-1835.

［8］张宇.HSDPA中QAM软解调算法实现和性能分析［J］.中国新通信，2010，（3）:48-50.

［9］李正明，姚如贵，王伶，等.基于G.9960协议的高阶QAM调制与解调［J］.微电子学与计算机，2011，28 （3）:89-93.

［10］MOHAMMAD M.A turbo-decoding message-passing algorithm for sparse parity-check matrix codes［J］.IEEE Transaction on Signal Processing，2006，54（11）: 4376-4392.

［11］周相超，赵旦峰，薛睿.深空通信系统中高阶LDPC码的软定时同步算法［J］.哈尔滨工业大学学报，2014，46（3）:110-114.

［12］SHAHNAZ B.Textbook of engineering mathematics: special functions and complex variables［M］.New Delhi:Prentice-Hall Of India Pvt.Limited，2008.

［13］HARTMANN A K.Practicalguidetocomputer simulations［M］.Singapore:World Scientific，2009.

（编辑 苗秀芝）

Low complexity de-mapping algorithm of cross-constellation QAM in G.HN

XU Juan1，YAO Rugui2，NAN Huani2，GAO Fanqi2
（1.School of Electronic and Control Engineering，Chang′an University，710064 Xi′an，China；2.School of Electronics and Information，Northwestern Polytechnical University，710072 Xi′an，China）

To reduce the de-mapping complexity of cross-constellation QAM in G.HN standard，we first introduce a novel concept of contribution weight to evaluate the contribution of given constellation to the loglikelihood ratio.With its help，a low complexity de-mapping algorithm within shrunk search range is proposed.And then，some boundary conditions are analyzed and solved.Furthermore，an adaptive configuration of search range is also presented with the assistance of channel estimation.The simulation result validates that the proposed algorithm downsizes the search range without any sacrifice of performance.2 048-QAM and 512-QAM shrink their average of searching constellations to 1.9%and 5.7%respectively of the whole constellations.Therefore，the proposed algorithm makes good tradeoffs between performance and complexity，and is expected to have important engineering value and widely application foreground.

quadrature amplitude modulation（QAM）；cross-constellation；de-mapping；channel estimation （CE）；search range；contribution weight

TN914.43

A

0367-6234（2015）05-0110-08

10.11918/j.issn.0367-6234.2015.05.019

2014-03-14.

航天支撑基金（2013-HT-XGD）；陕西省自然科学基础研究计划资助项目（2014JM2-6094）；国家自然科学基金（61271416）.

徐 娟（1980—），女，博士，讲师.

徐 娟，xuj@mail.nwpu.edu.cn.