不确定载荷下刚架体结构稳健优化设计
杨继超,戴宗妙
(1.哈尔滨工程大学机电工程学院,黑龙江哈尔滨150001;2.中国船舶重工集团公司第七一三研究所,河南郑州450015)
优化设计是指在特定约束条件下,获得结构某种性能指标(如体积、质量或扰度等)最优。传统的优化设计,往往建立在确定性模型基础上,没有考虑变量参数实际值与名义值存在的差异,得到的优化解位于可行域边界。当实际工程中变量参数(如载荷)发生扰动时,理论最优解很可能落在不可行区域,给设计带来潜在风险。针对工程设计中不确定性,国内外学者提出许多设计理论和方法。其中稳健设计基本思想是在不消除不确定性源的前提下,提高产品对不确定因素抵抗力[1]。结构稳健优化一个难点是对不确定性力的分析及对优化过程影响,即建立不确定性优化模型。
目前,基于概率不确定模型应用比较成熟。文献[2-4]通过构造约束和目标函数灵敏度分析,进行稳健优化设计;文献[5]采用Kriging模型,建立以目标性能指标均值和方差为优化目的优化模型;文献[6]将稳健优化问题转化成多目标优化问题,对结构进行优化设计;为了提高计算效率,文献[7]基于随机响应量前四阶矩建立稳健优化设计模型。基于概率模型方法需要大量样本数据估算参数的不确定度或分布函数,而这些数据在实际工程中往往很难实现。然而获得不确定因素的边界,是相对容易的。非概率方法就是根据不确定参数未知但有界的特点进行建模。文献[8-10]提出了基于凸集理论的非概率不确定模型分析方法,对结构进行稳健性分析。文献[11]在非概率凸模型可靠性约束下,通过超椭球域界定不确定参量,进行结构优化设计。文献[12-13]运用区间模型对不确定性参数进行非概率性描述,建立结构优化和设计方法。目前,在集合理论凸模型中,大多方法都是求解结构响应上下界解析解的近似值[14];对于复杂的结构,区间模型计算量往往非常大,计算效率低下甚至无法实行。
20世纪90年代,Ben-Haim提出非概率Information-Gap(I-G)理论描述不确定性模型,并以系统承受最大不确定性波动作为评价结构稳健性的指标。文献[15-16]给出了非概率的I-G模型处理不确定性的理论方法,文献[17-18]基于I-G理论,对地下结构在非确定因素影响下结构的稳健性进行分析。为此,本文针对刚架体结构承受不确定载荷特点,引入I-G理论,建立结构非概率稳健性模型,并结合优化设计方法,对刚架体结构进行稳健性优化设计,提高对不确定因素的抵抗能力。
1 不确定载荷I-G模型
1.1 刚架体应力约束方程
在实际工程中,刚架体结构通常会受到不确定载荷作用,且结构需要满足最基本应力约束要求。令一个线弹性的三维刚架体结构自由度为n,则系统平衡方程为

式中:u∈Rn和f∈Rn分别表示节点的位移和外载荷矢量,K∈Sn为刚度矩阵。对于有m个杆件的刚架体结构,杆截面积a=(ai)∈Rm,则K可以写成如下形式:

式中:b=(bij)∈Rn是常向量。则由上述关系式,应力约束方程为

式中:E表示弹性模量,表示第i杆许用应力。根据位移表示约束方程,则有

式中:dl∈R,常量vl∈R。为了保证刚架体结构的安全稳定,杆件必须满足式(3)或式(4)。当上述约束关系式满足时,不确定变量允许一定的变化幅度。这里通过稳健函数来度量,它与影响刚度矩阵的杆截面积和不确定程度相关。
1.2 不确定性因素I-G分析
I-G模型是由凸集理论基础发展而来。根据I-G理论,不确定度是采用已知信息与未知信息的偏离程度或断缺状态描述。由于外在环境的不可控性以及所需解决问题信息掌握贫乏,结合刚架体结构特点,建立不确定性影响因素的I-G模型。不确定参数不确定性程度可表达为[17]


式(6)表明,当不考虑载荷不确定性(α=0)时,名义载荷即为实际载荷f,I-G模型退化成确定性模型。式(7)表明,不确定参数α决定不确定因素真实值和名义值之间的偏离程度,当α小时,和f越接近;反之偏离程度大。相比较其他非概率模型,如固定区间模型或凸集模型,I-G模型U(α,)的嵌套凸集特性能更好反应不确定性载荷的动态变化。
1.3 基于I-G模型稳健函数构造
稳健性反映结构对不确定性因素的抵抗程度,如果结构能够允许较大不确定性变化而不失效,就认为该结构稳健强。上一节,建立了不确定载荷的I-G模型,定义参数α表示不确定性变化幅度。
在满足约束条件式(3)或(4)的前提下,结合I-G理论,刚架体结构系统的平衡方程(1)所有可能解集可表示成


结合式(4)、(8),式(9)的最优规划问题可表示为

式(10)即为稳健函数。对于两组不同刚架体截面积向量a1∈Rn和a2∈Rn,如果则a1比a2稳健。
2 结构稳健优化模型
2.1 一般优化模型形式
传统的确定性问题数学优化模型可以表示为

式中:f(x)为优化模型的目标函数,x优化设计变量;gi(x)和n分别为约束条件以及约束条件数量;x1、x2为设计变量的取值范围。
当存在不确定因素时,结构稳健优化不但要考虑不确定因素对优化模型的影响,还要考虑目标函数的稳健性,即能抵御不确定因素的影响。结合上一节的分析,注意到稳健函数值大的结构更为强健。基于优化理论,建立稳健函数最大化问题的优化模型。考虑结构体积(质量)约束条件,横截面向量a应该满足:

式中:li>0 表示第i个杆长,为体积上限。对限定的位移uc和,应力约束下鲁棒函数最大化问题优化模型可以写为

优化目标为稳健性函数最优,即结构抵抗不确定性载荷最大化。
2.2 半定规划模型
上述过程中,基于I-G模型处理不确定载荷,则载荷集中包含无穷多载荷,常规方法很难对上式进行求解。因此通过半定规划对稳健优化模型进行重新构造。传统半定规划的数学形式为[14]

式中 c,x∈Rn,Fi(i=0,…,n)为n阶常对称矩阵,x 为设计变量,矩阵F(x)≽0为正定。
结合本文优化模型式(13),令F⊂Rn表示满足上述应力约束(4)的力集合:
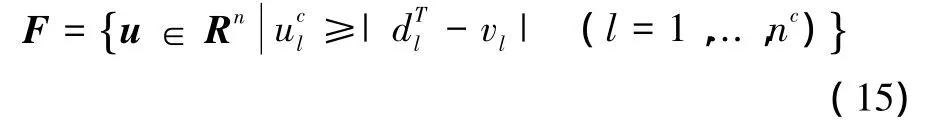

进行如下定义:

其中,p,t∈R,a∈Rm。将新参数(t,p)引入稳健函数(a,uc)中,则可以得到:


半定规划算法有成熟的商业计算软件包,可直接方便快捷调用,避免如牛顿法那样推导雅可比矩阵和海森堡矩阵。
3 数值仿真
3.1 三杆系稳健性优化
考虑如图1所示的三杆件架体。其形式为对称结构,杆件个数和自由度分别为m=3,n=2。为了结果分析方便,这里将单位归一化处理。杆件3的长度l3=15且垂直于水平方向,θ=45°。杆件所受力状态如图1所示,名义载荷大小为100。考虑应力约束式(3)=3.0(i=1,2,3)。设定结构初始变量为a0=(20,20,20),以a=a0时结构体积为基准,则结构体积约束为≤1 148.53。

图1 三杆架体Fig.1 3-bar structure
已知初始变量值a0,对式(18)进行求解,得到(a0,σc)=0.822。通过半定规划模型式(19),对架结构进行优化设计,得到优化迭代过程如表1。

表1 优化迭代过程Table 1 Iteration history of the optimization
对结构初始状态a0进行分析。随机产生一组力f,使其落在稳健函数(a0,σc)限定的不确定载荷集之中。则结构中杆件应力σi(i=1,2,3)分布状态如图2所示。
经过观察可以发现,杆件3在应力σ3=3.0附近有分布,而杆件1(或杆件2)应力值始终没有发挥最大功效。
刚架经过优化后,最优解为a=a*,经过计算和分析,得到结构杆件应力σi(i=1,2,3)分布状态如图3所示。其中,应力约束σi≤σc(i=1,2,3)在3个杆件中均产生作用,优化后改善了结构性能,最大程度发挥了刚架体结构的潜力。

图2 当a=a0时杆件应力分布Fig.2 Stress states of the 3-barstructure with a=a0

图3 当a=a*时杆件应力分布Fig.3 Stress states of the 3-barstructure with a=a*
3.2 多杆系刚架体结构
如图4所示多杆架体结构,杆件个数和自由度分别为m=100,n=90。杆件在x轴和z轴方向的长度均为100,在y轴方向有杆长100和30(即中部连接处短杆)2种规格,其余为连接斜杆。结构底座完全约束。载荷作用于如图4所示位置,垂直方向载荷名义值为=(0,10,0);水平方向名义值=(2,0,0)。
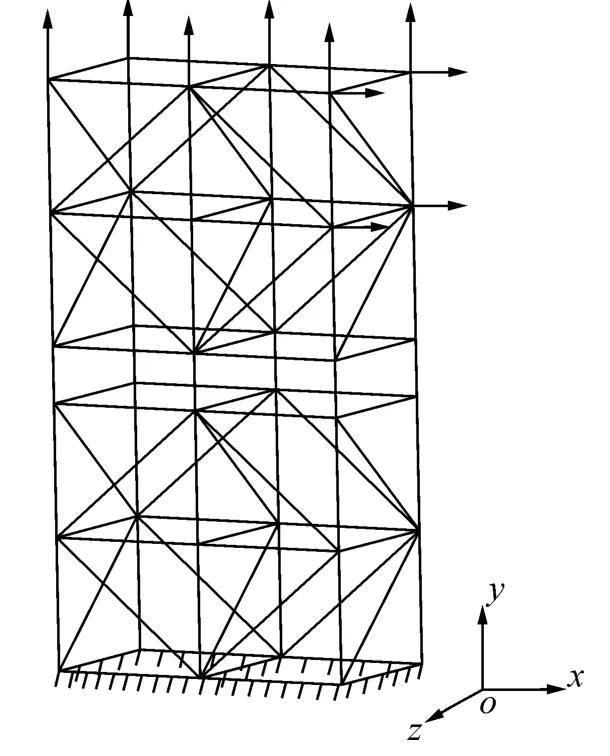
图4 多杆架结构Fig.4 Complex frame structure

图5 架体优化设计Fig.5 Optimal design of the frame structure
为了验证优化结果,观察后标记如图6所示,对部分杆件进行分析。当结构中a=a0和a=a*时,产生一组随机摄动载荷分别满足应力约束式(3)要求。

图6 架体平面结构Fig.6 2-D structure of the frame structure

图7 随机摄动载荷下最大应力Fig.7 Fluctuation stress under random loading
图7表示优化前后对比,即对应a=a0、a*时,图6中标记对应杆杆件最大应力变化范围。其中浅色为设计变量初始取值,深色为优化后取值。通过观察发现,优化后结构在随机摄动载荷下,最大应力变化幅值总体上小于优化前,结构保持较大的安全富裕度,能更好抵抗不确定载荷的影响。
4 结束语
本文基于稳健性函数构建了刚架体结构稳健性优化算法。该方法充分考虑了载荷的不确定因素,利用I-G理论处理不确定载荷,构造应力约束下的稳健性函数最大值优化模型,利用半定规划松弛技术重新将优化问题转换成半定规划问题,降低工程设计人员求解的难度,提高求解效率。通过数值仿真可以发现在优化过程中约束条件发挥作用,在同等体积(质量)条件下,虽结构局部一些杆件应力有所增加,但总体应力状态得到改善,提高了结构抗扰动载荷的能力。
[1]TAGUCHI G,CHOWDHURY S,TAGUCHI S.Robust engineering[M].New York:McGraw-Hill,2000:327-533.
[2]张瑞军,邱继伟,贾庆轩,等.基于灵敏度附加项的多目标可靠性稳健优化设计[J].应用基础与工程科学学报,2013,21(4):777-785.ZHANG Ruijun,QIU Jiwei,JIA Qingxuan,et al.Multi-objective reliability-based robust optimization design based on the sensitivity additional items[J].Journal of Basic Science and Engineering,2013,21(4):777-785.
[3]丁力平,冯毅雄,谭建荣,等.基于性能稳健指数的产品族稳健优化设计[J].计算机集成制造系统,2010,16(6):1121-1130.DING Liping,FENG Yixiong,TAN Jianrong,et al.Robust optimization design of product family based on performance robustness index[J].Computer Integrated Manufacturing Systems,2010,16(6):1121-1130.
[4]高一聪,冯毅雄,谭建荣,等.基于MSRE的机械产品质量特性稳健优化设计方法[J].计算机集成制造系统,2010,16(5):897-904.GAO Yicong,FENG Yixiong,TAN Jianrong,et al.Product quality characteristics robust optimization design based on minimum sensitivity region estimation[J].Computer Integrated Manufacturing Systems,2010,16(5):897-904.
[5]李小刚,程锦,刘振宇,等.基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J].机械工程学报,2014,50(3):65-173.LI Xiaogang,CHENG Jin,LIU Zhenyu,et al.Robust optimization for dynamic characteristics of mechanical structures based on double renewal kriging model[J].Journal of Mechanical Engineering,2014,50(3):165-173.
[6]于利磊,唐文勇,张圣坤,等.一种工程结构的鲁棒优化设计方法[J].上海交通大学学报,2003,37(8):1189-1192.YU Lilei,TANG Wenyong,ZHANG Shengkun,et al.Robust optimization design method for engineering structures[J].Journal of Shanghai Jiaotong University,2003,37(8):1189-1192.
[7]宋述芳,吕震宙.基于高阶矩的稳健优化设计研究[J].力学学报,2012,44(4):735-744.SONG Shufang,LYU Zhenzhou.The robust optimization design based on moment estimation method[J].Chinese Journal of Theoretical and Applied Mechanics,2012,44(4):735-744.
[8]BEN H Y,ELISHAKOFF I.Convex models of uncertainty in applied mechanics[M].Amsterdam:Elsevier,1990:175-230.
[9]BEN-HAIM Y.Robust reliability of structures[J].Advances in Applied Mechanics,1997,33:1-41.
[10]张成,吴慧,高博青,等.非概率不确定性结构的鲁棒性分析[J].计算力学学报,2013,30(1):51-56.ZHANG Cheng,WU Hui,GAO Boqing,et al.Analysis of structural robustness with non-probabilistic uncertainties[J].Chinese Journal of Computational Mechanics,2013,30(1):51-56.
[11]王晓军,王磊,贾晓,等.基于非概率凸模型可靠性的结构优化设计[J].北京航空航天大学学报,2012,38(5):630-635.WANG Xiaojun,WANG Lei,JIA Xiao,et al.Structural optimization design based on non-probabilistic convex modeling reliability[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(5)630-635.
[12]刘晓,徐格宁,杨萍.区间干涉模型下的非概率可靠性应用研究[J].中国矿业大学学报,2012,41(4):675-680.LIU Xiao,XU Gening,YANG Ping.Application of nonprobabilistic reliability based on interval interference model[J].Journal of China University of Minging & Technology,2012,41(4):675-680.
[13]石海军,钱林方,徐亚栋,等.具有参数区间不确定的机械臂结构优化[J].南京理工大学学报,2014,38(1):100-105.SHI Haijun,QIAN Linfang,XU Yadong,et al.Structural optimization for manipulator with interval uncertainties[J].Journal of Nanjing University of Science and Technology,2014,38(1):100-105.
[14]WOLKOWICZ H,SAIGAL R,VANDENBERGHE L.Handbook of semidefinite programming:theory,algorithms,and applications[M].(s.l.):Kluwer Academic Publishers,2000:137-201.
[15]YAKOV B H.Set-models of information-gap uncertainty:axioms and an inference scheme[J].Journal of the Franklin Institute,1999,336:1093-1117.
[16]YAKOV B H.Uncertainty,probability and information-gaps[J].Reliability Engineering and System Safety,2004,85:249-266.
[17]苏永华,李翔.基于Info-Gap理论的地下结构稳健性分析方法[J].岩土工程学报,2011,33(2):227-233.SU Yonghua,LI Xiang.Robust reliability analysis for underground structures based on Info-Gap theory[J].Chinese Journal of Geotechnical Engineering,2011,33(2):227-233.
[18]曹文贵,李媛,翟友成.基于Info-Gap理论的基桩下伏岩溶顶板稳定性的主动分析方法[J].岩石力学与工程学报,2013,32(2):393-400.CAO Wengui,LI Yuan,ZHAI Youcheng.Active analysis method for stability of karst roof under foundation pile based on info-gap theory[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(2):393-400.

