基于SVM的决策融合鱼类识别方法

杜伟东，李海森，魏玉阔，徐超

(1.哈尔滨工程大学水声技术重点实验室，黑龙江 哈尔滨150001;2.哈尔滨工程大学水声工程学院，黑龙江 哈尔滨150001)

鱼类识别是渔业资源评估中重要手段之一，虽然目前已有多种方法来进行鱼类识别［1-3］，然而鱼是一个复杂的声散射体，鱼体及鱼鳔的方位、大小、形状严重影响鱼的声散射特征，特别是对于有鳔鱼种，鱼鳔是散射信号的主要贡献体，而鱼鳔是外表面不规则的散射体，导致鱼在不同声散射方位上表现的散射特性是不同的［4］，因此单一方位探测势必会丢失鱼的散射信息。而且鱼在水中是自由游动的，探测时不能预见鱼在波束内的具体方位，因此实际环境下获得鱼的声散射特性在单一散射方位上表现出一定的随机性，造成在鱼类识别过程中存在由于鱼的方位不同引起的分类正确率低、甚至不能正确分类的问题，而多方位声散射数据融合方法同时利用了鱼在多个方位的声散射特性，这种方法在水下目标识别领域有所应用［5-6］，本文结合鱼声散射特性的研究，从多方位声散射数据决策层融合角度出发，利用小波包变换(wavelet packet transform，WPT)、离散余弦变换(discrete cosine transform，DCT)进行基于上述特性的特征提取，利用支持向量机(SVM)对提取的特征做出决策，并通过决策层融合的方法得到最终识别结果。

1 鱼声散射特性分析及特征提取

1.1 声散射特性理论分析

对于有鳔鱼种，由于鱼鳔的存在使得相同鱼种在不同方位上表现的散射特性是不同的，但是对于类别上的表现是相关的，而不同鱼种由于鱼鳔形状不同，导致在多个方位上都表现出了不同的声散射特性。多方位数据融合鱼类识别方法能同时利用多个方位的鱼声散射信息进行鱼类识别，有效解决了在鱼类识别过程中只利用单方位声散射信息存在的问题，进而提高识别率。

1.2 多方位声散射数据获取实验方案

选取3种鱼作为识别对象，即鲫鱼、金鳟、鲤鱼，其中鲤鱼选取大小不同的2条，定义为小鲤鱼、大鲤鱼，实验用鱼体照片如图1所示，实测鲫鱼、金鳟、小鲤鱼、大鲤鱼叉上分别为 26、35、33、41 cm。

图1 鱼体照片Fig.1 Fish body photos

图2为多方位声散射数据获取方法示意图，其中中间黑色点代表发射换能器，两侧灰色点代表接收换能器，相邻换能器之间距离为30 cm。基于现有条件，利用单只标准水听器代替接收换能器，在不同方位采集鱼的声散射信号，是实际应用中，可以利用多个接收换能器组成图2所示的结构，同时获取鱼在不同方位上的声散射信号。

图2 多方位声散射数据获取示意图Fig.2 Multi-azimuth acoustic scattering data acquisition schematic

针对上述鱼种在哈尔滨工程大学水声技术重点实验室消声水池进行了水池实验，水池进行了6面消声处理。主要实验设备为发射换能器、标准水听器、采集器、激光笔等。实验现场如图3所示，发射换能器朝向鱼体发射声脉冲信号，水听器接收鱼的声散射信号，并由采集器进行采集。实验过程中采用了防水激光笔，利用激光笔发射出来的绿色细光束强光确保发射波束中心正对鱼中心。发射换能器中心频率150 kHz，带宽40 kHz，换能器沿轴线方向发射声CW脉冲信号，波束角度 3.8°，脉宽 0.05 ms。换能器与鱼体之间距离4 m，满足远场条件。

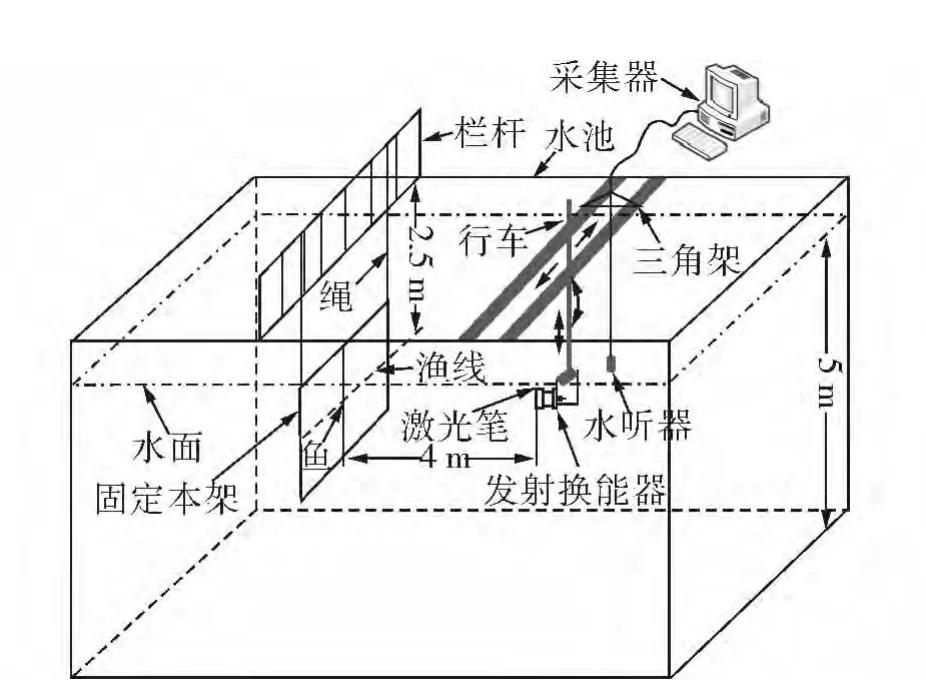
图3 实验现场示意图Fig.3 Experiment site schematic

1.3 特征提取与降维

如图4所示，特征提取主要包括小波包变换、小波包子带能量、离散余弦变换、特征降维等步骤，子带能量体现了鱼在不同频带的响应信息，离散余弦变换则体现了鱼在形状上表现的散射特征信息。

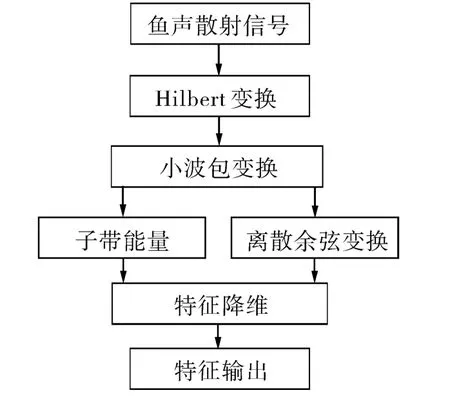
图4 特征提取流程图Fig.4 Flow chart of features extraction

1.3.1 特征提取

小波包变换是获取信号局部特征的良好工具［7］。不同形状的鱼，其内部解剖结构差异较大，其各个部分对散射信号的贡献是有差异的，散射信号会表现出不同的能量分布特性。因此，对单体鱼散射信号进行小波包变换，则小波包子带能量体现了鱼声散射信号的在不同频带内的能量分布特性。

离散余弦变换是一种实数域变换，其变换核为实的余弦函数，并具有算法快速及系数分布比较集中的特点，且利用很少的系数集中了信号大部分的能量，其主要用来表征不同形状目标的特征。

对于鱼的声散射信号x(n)，n=0，1，…，N－1，其离散余弦变换定义为

其中，

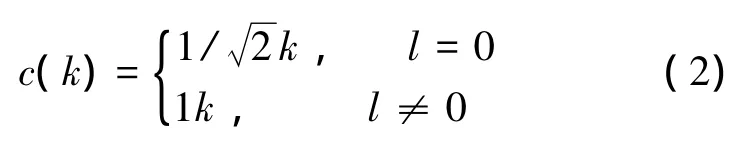
式中:k=0，1，…，N－1;x(l)为特征量，l=0，1，…，L－1为特征量个数。对鱼散射信号进行Hilbert变换，求解信号包络，对包络信号进行小波包变换，每个子带的频宽为

式中:N为小波包分解层数，采样率为fs=1 MHz，进行6层小波包分解，计算得出每个子带频宽约为7.8 kHz。图5为第1个方位下3种鱼散射信号频谱，频域响应波动集中在50 kHz内，由式(3)计算需要6.4个子带能覆盖50 kHz的频宽，6层小波变换共产生64个子带，此处取6个子带。

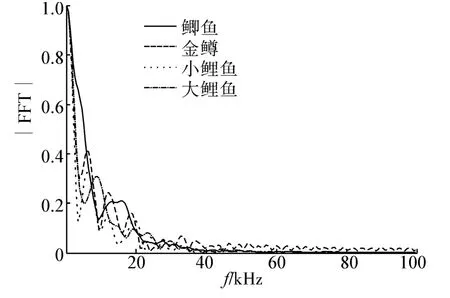
图5 鱼散射信号频谱Fig.5 Fish scattering signal spectrum

对包络信号进行dB4小波包分解，并进行重构，设小波包重构序列Sj，k，则各频带的能量表示为

式中:j=1，2，…，6 为接收方位号，k=1，2，…，6 为小波包节点号，则构成的特征向量为

图6 小波包子带能量Fig.6 Wavelet packets sub-band energy

图6为提取得到第1个方位声散射信号的小波包子带能量，可以看出，3种鱼的小波包子带能量表现出不同的分布特性，相对而言，大鲤鱼和小鲤鱼有较为相近的能量分布特性。

在得到小波包子带的基础上，对子带进行离散余弦变换，变换后波动主要集中在前14个系数，故取每个子带的前14个离散余弦变换系数作为特征量，对于离散余弦变换系数序列Dj，k，构成的特征向量为

式中:j=1，2，…，6 为接收方位号，k=1，2，…，6 为小波包节点号。

第1个方位下得到的第1个子带离散余弦变换系数如图7所示，可以看出，3种鱼的离散余弦变换系数表现出不同的分布特性，相对而言，大鲤鱼和小鲤鱼有较为相近的分布特性。

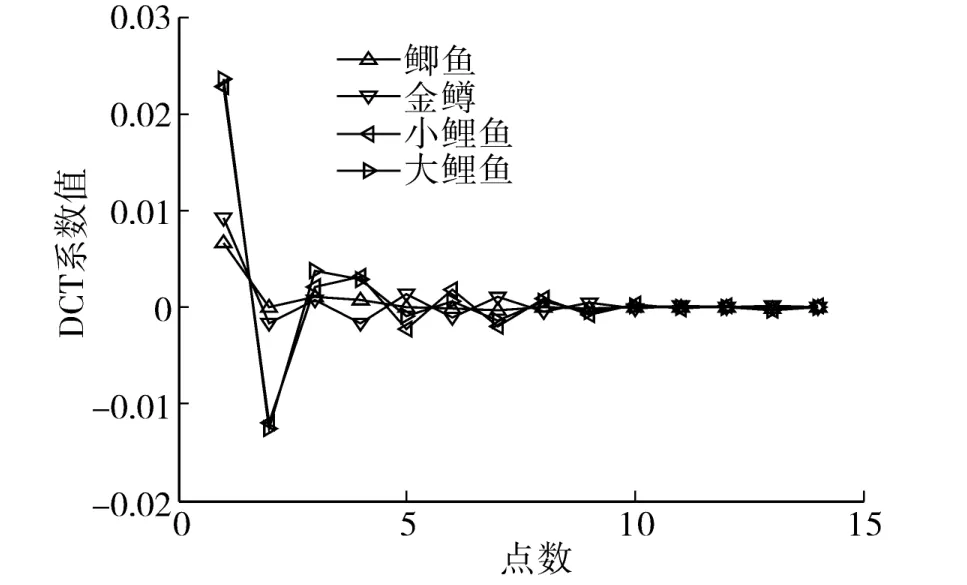
图7 子带离散余弦变换系数Fig.7 Sub-band discrete cosine transform coefficients

将小波包子带能量与离散余弦变换系数特征进行组合，共得到90个特征值，特征向量为

1.3.2 特征降维

上述特征提取方法得到的特征维数较高，高维特征对于鱼类识别具有不同贡献。有些特征对于识别的贡献较大，有些特征则不是。因此，对高维特征进行降维处理，保留对识别贡献大的特征，对提高识别率和结果稳定性具有十分重要的意义。

通过Fisher判别函数判断每个类之间对应特征的距离［8］，从而得到每个特征对识别的贡献能力，Fisher判别函数表示为

式中:i、j代表类别;分别为类i、j特征样本的均值与方差。经过判别，贡献能力大的特征被保留下来组成新的特征向量。利用Fisher函数判别时，小鲤鱼、大鲤鱼的特征向量各取一部分样本组成鲤鱼特征向量的样本集合，鲤鱼、金鳟、鲫鱼特征样本集合样本数相等，图8分别为2类鱼样本特征判别比、3类鱼样本特征判别比。

其中，前6个结果为小波包子带能量特征量判别比，后84个结果为小波包子带离散余弦变换系数特征量判别比。经验证发现，判别门限设置为3.84时识别效果最佳，此时保留的特征量总个数为49个，其中5个子带能量特征，44个子带离散余弦变换系数特征。同时可以看出，鲫鱼、金鳟之间特征判别距离整体上略小于二者分别与鲤鱼之间的判决距离。

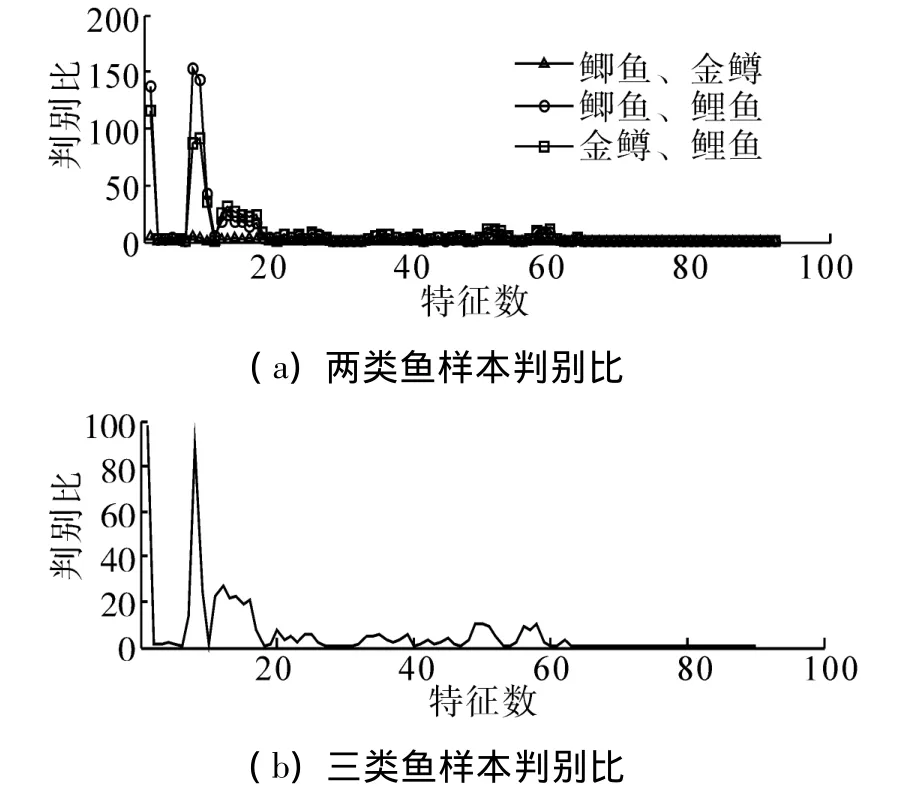
图8 Fisher判别比Fig.8 Fisher discrimination ratios

2 分类器与多方位数据决策融合

在水下目标识别领域，SVM因具有较低的分类误差而被认为是一种性能较佳分类器［9］。它通过由内积函数定义的非线性变换将低维的输入空间转化为某个高维空间，将非线性分类问题变换为线性分类问题，并在高维空间中求解广义最优分类面。

图9为决策融合算法结构，A个方位的声散射数据单独进行提取特征，各个方位的特征量单独通过SVM分类器，决策结果表示成后验概率的形式，将概率融合为一个整体概率向量，输入至下一级SVM分类器，得出最终分类结果，这种方法的特点是利用多方位数据进行多次决策，得到高精度的鱼类识别结果。

图9 决策融合算法结构Fig.9 Decision fusion algorithm structure

对于非线性可分SVM，有

存在一个决策边界，此时SVM的输出为

如果不考虑其中的符号函数运算，则SVM输出了样本与最大边缘超平面之间的距离，但是SVM并不能直接得到后验概率［10］。

SVM实际上是一个2类分类器，在Cl类情况下，可以采用“一对一”或“一对多”方式，在“一对多”方法中，对于k分类则需要训练k个分类器，则得出k个决策超平面，样本离第i个决策超平面越远，分类正确的可能性越大，即属于第i类。因此，可以将输出的距离表示为

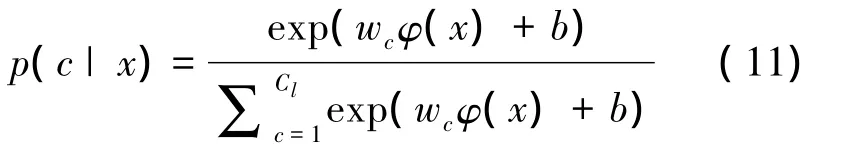
则每个方位输出的后验概率向量为

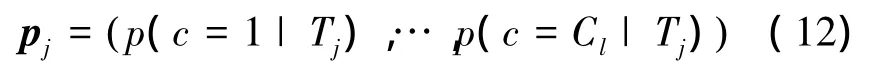
将每个方位的后验概率向量进行组合，得到的多方位决策后验概率为

将组合后的概率作为特征向量，输入下一级SVM，做出最终类决策。

3 识别性能

每个方位1 000组采样数据，其中500组作为分类器训练样本，剩余500组作为分类器测试样本，通过随机抽取样本的方式构建训练集与测试集。选取径向基函数为SVM分类器核函数，代价系数和高斯滤波器宽度采用基于交叉验证的网格搜索方法寻找最优值。

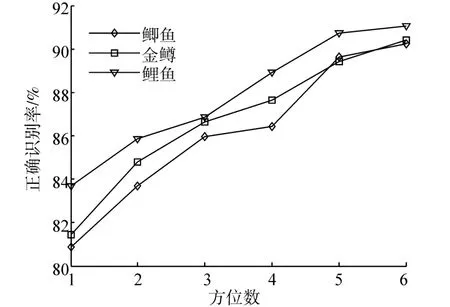
图10 不同方位数下的正确识别率Fig.10 The identification rates under different numbers of azimuths

采用降维后的子带能量、子带离散余弦变换系数组合特征作为特征向量对3种鱼进行识别。如图2所示，自下而上依次取1～6个接收方位，在不同方位数量情况下识别率如图10所示。可以看出，随着方位数量的增加，识别率呈升高趋势，其中鲤鱼识别率总体高于鲫鱼、金鳟识别率，鲫鱼、金鳟识别率曲线变化趋势相似，与Fisher判别函数对特征的判别结果相对应，这也进一步说明特征降维方法的有效性。识别率最终达到90%以上，表明多方位数据决策层融合方法具有更优的鱼类识别性能。

为进一步检验识别性能，采用大、小鲤鱼样本互相验证的方式，即大鲤鱼样本、小鲤鱼样本分别作训练样本、测试样本进行测试，识别结果如图11所示。可以看出，大鲤鱼作训练样本、小鲤鱼作测试样本，小鲤鱼作训练样本、大鲤鱼作测试样本都具有很高的识别率，而且随着方位数的增加呈升高趋势，进一步验证了方法的有效性。

图11 鲤鱼互相验证正确识别率Fig.11 The identification rates of carp under cross validation

4 结论

本文研究了基于小波包子带能量及离散余弦变换系数特征的多方位声散射数据决策层融合鱼类识别方法，并进行了实验设计与验证，得出如下结论:

1)通过小波包变换与离散余弦变换得到的特征从不同角度描述了不同种类鱼声散射特性上的差异性，针对特征维数高的特点，通过Fisher判别方法有效降低了特征降维，可以为有效进行鱼类识别提供性能稳健的特征。

2)将决策结果通过SVM的输出表示成后验概率的形式，并对后验概率进行二次决策，通过这种多方位数据决策层融合，并进行多次决策的识别方法，三类鱼的整体识别率呈升高趋势，方法效果明显。

3)方法本质是取决于不同鱼种鱼鳔本身的不同，以及其在多个方位上的声散射特性，实验所选择的目标鱼种并没有特别的针对性，样本具有完全的随机性，表明所提出的方法具有一定普遍性。

［1］ROBOTHAM H，BOSCH P，CARLOS J，et al.Acoustic identification of small pelagic fish species in Chile using support vector machines and neural networks［J］.Fisheries Research，2010，102(1/2):115-122.

［2］LUNDGREN B，NIELSEN J R.A method for the possible species discrimination of juvenile gadoids by broad-bandwidth backscattering spectra vs.angle of incidence［J］.ICES Journal of Marine Science，2008，65(4):581-593.

［3］SLAS-CITAL A，ATKINS P R，FOO K Y.Broadband amplitude and phase sonar calibration using LFM pulses for high-resolution study of hard and soft acoustic targets［C］//OCEANS 2011，Spain，2011:1-8.

［4］LIU G，JAYATHILAKE P G，KHOO B C.Conformal mapping for the Helmholtz equation Acoustic wave scattering by a two dimensional inclusion with irregular shape in an ideal fluid［J］.Journal of the Acoustical Society of America，2012，131(2):1055-1065.

［5］CARTMILL J，WACHOWSKI N，AZIMI-SADJADI M R.Buried underwater object classification using a collaborative multi-aspect classifier［J］.IEEE Journal of Oceanic Engineering，2009，34(1):32-44.

［6］杜伟东，李海森，陈宝伟，等.一种基于声散射特性的有鳔鱼特征获取方法［J］.应用声学，2014，33(6):505-511.DU Weidong，LI Haisen，CHEN Baowei，et al.Features acquisition of fish with swim bladder baesd on acoustic scattering characteristics［J］.Journal of Applied Acoustics，2014，33(6):505-511.

［7］张汝波，张鑫瑜，李雪耀.利用支持向量机和高阶累量实现飞机类型识别［J］.哈尔滨工程大学学报，2010，31(3):366-370.ZHANG Rubo，ZHANG Xinyu，LI Xueyao.Recognizing aircraft type using a support vector machine and a higher order cumulant［J］.Journal of Harbin Engineering University，2010，31(3):366-370.

［8］AZIMI-SADJADI M R，YAO D，JAMSHIDI A，et al.Underwater target classification in changing environments using an adaptive feature mapping［J］.IEEE Transactions on Neural Networks，2002，13(5):1099-1111.

［9］LI D，AZIMI-SADJADI M R，ROBINSON M.Comparison of different classification algorithms for underwater target discrimination［J］.IEEE Transactions on Neural Networks，2004，15(1):189-194.

［10］石强，陈凤娥，梅天灿，等.SVM后验概率结合改进多尺度MRF的遥感影像分割方法［J］.武汉大学学报信息科学版，2013，38(2):195-199.SHI Qiang，CHEN Feng’e，MEI Tiancan，et al.Remote sensing image segmentation based on SVM posterior probability and improved multi-scale MRF［J］.Geomatics and Information Science of Wuhan University，2013，38(2):195-199.