加热面边界条件对MEB形成过程的影响
唐继国,阎昌琪,孙立成,朱光昱
(1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨150001;2.四川大学水力学与山区河流开发保护国家重点实验室,四川成都610065)
在未来的核能、电子和航空航天等领域中,气泡微细化沸腾(microbubble emission boiling,MEB)因其超高的换热能力而被认为是一种很有潜力的冷却方法。气泡微细化沸腾是指在一定过冷度下的一种特殊沸腾过程,MEB发生时加热面的热流密度远远超过临界热流密度(CHF),并伴随气泡破裂,大量微小气泡喷射的过程。日本学者Inada等[1-2]用铜块,Tange等[3-4]用铂丝作为加热元件,对池式气泡微细化沸腾进行了实验研究,发现过冷度是触发这一现象发生的关键因素。Kubo等[5]发现气泡微细化沸腾实验中的加热面由于气泡破裂会被严重侵蚀。Kumagai等[6]用高速摄影仪分别测量出在气泡微细化沸腾过程中气膜的高度、宽度和破碎频率。俄罗斯学者Zeigarnik等[7-8]认为气泡微细化沸腾过程中喷射的微小气泡为不凝性气体。目前,气泡微细化沸腾的形成机理和发生条件还尚不清楚。由于加热面周边边界条件对于MEB的发生具有重要影响,通过改变加热面相对位置,可以使加热面周围的边界条件发生变化,以研究其对MEB发生过程的影响。本文通过实验和数值分析方法,研究加热面边界条件对于MEB发生过程的影响,进一步探究Marangoni对流和气液界面上冷凝过程在MEB形成过程中的作用。
1 实验装置和实验现象
1.1 实验装置
气泡微细化沸腾实验装置如图1所示,加热面直径10 mm。3根直径1 mm分别距离加热面3、5.8、8 mm的铜-康铜热电偶安装在铜芯上用于测量温度推导热流密度和壁面过热度。3根热电偶测点均位于铜芯轴线上。水的过冷度用1根置于水箱中距加热面约5 mm处,直径1 mm的铜-康铜热电偶测量。4个加热功率可调节的硅碳棒通过辐射换热加热铜芯。过冷度的调节和维持是通过调节水箱中电加热器的加热功率和冷却器内冷却水流量实现的。水箱观察窗附近布置高速摄影仪(Fastcam SA5)以及背光系统用于捕捉气泡行为。在铜芯与陶瓷绝热环之间装有一个密封用的石棉垫片,通过调整其厚度改变加热面与水箱底部的相对位置。图2示出实验中2种加热面相对位置:齐平加热面(加热面与水箱底部齐平)与下沉加热面(加热面比水箱底部低约0.5 mm)。

图1 实验装置简图Fig.1 Schematic diagram of experimental setup

图2 加热面相对位置简图Fig.2 Schematic diagram of relative position of heating surface
1.2 气泡行为
50 K过冷度、62 K左右壁面过热度条件下,齐平加热面和下沉加热面上的气泡行为分别示于图3和图4。对于前者来说,气泡微细化沸腾剧烈发生,蒸汽气膜破裂,并伴有微小气泡喷射,热流密度高达5.6 MW/m2,远大于临界热负荷(CHF)。然而在下沉加热面上,气泡形成以后比较稳定,且几乎覆盖整个加热面,没有气泡微细化沸腾现象发生,换热能力较差,热流密度只有0.65 MW/m2。除此之外,从气泡产生到消失整个周期长达24.2 s,气液界面相对比较光滑,没有明显的界面波动现象发生。

图3 50K过冷度、62.5 K壁面过热度下齐平加热面上气泡行为Fig.3 Bubble behaviors at subcooling of 50 K and wall superheat of 62.5 K on flushing heating surface

图4 50K过冷度、62 K壁面过热度下下沉加热面上气泡行为Fig.4 Bubble behaviors at subcooling of 50 K and wall superheat of 62 K on embedded heating surface
2 数值模拟
为进一步分析加热面周围的对流过程对气泡微细化沸腾产生过程的影响,弄清两种加热面位置周围流动过程至关重要,利用数值分析软件分别对这两种情况下加热面上气泡周围的流场进行分析。
2.1 几何模型与网格划分
齐平加热面和下沉加热面条件的几何模型与局部网格划分分别如图5、6所示。由于加热面和气泡的对称性,在数值模拟中只考虑几何模型的四分之一。两种条件下的加热面都是一个直径10 mm的圆面,与实验装置中加热面直径尺寸相同。下沉加热面上的气泡是一个直径19.6 mm的局部球体,形状和大小与图4中7 s时的气泡接近。加热面下沉深度为0.5 mm,与实际相同。如图5(a)所示,该条件下的流体计算区域是一个边长35 mm的正方体。在齐平加热面上的气泡是一个长轴长8 mm、短轴长1 mm的局部扁椭球形。如图6(a)所示,该条件下的流体计算区域长、宽、高分别为35、35和20 mm。
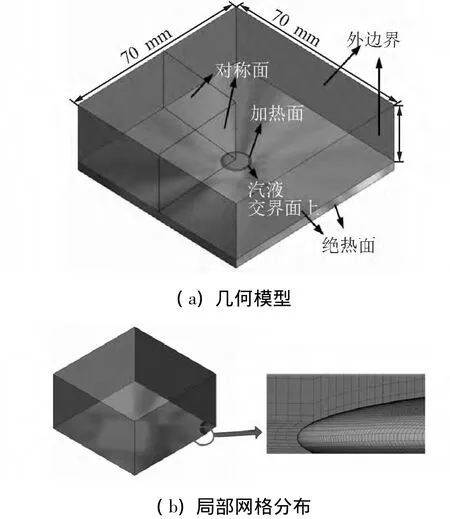
图5 齐平加热面条件下几何模型和局部网格分布Fig.5 Geometry and mesh of numerical simulations for flushing heating surface

图6 下沉加热面条件下几何模型和局部网格分布Fig.6 Geometry and mesh of numerical simulations for the case of the heating surface embedded
在两种加热面条件下,整个计算区域采用结构化网格,气泡附近通过增加节点数来进行加密,如图5(b)和图6(b)所示。对于齐平加热面的模拟,总网格数目是948 779;对于下沉加热面的模拟,总网格数目是998 457。
2.2 数学模型与数值计算
50 K过冷度、62 K过热度条件下,在两种加热面上都会覆盖有一个较大的气泡。在齐平加热面上会发生气泡微细化沸腾现象,气泡迅速破裂如图3所示;但在下沉加热面上却未发生气泡微细化沸腾现象,气泡可以平稳地在加热面上逐渐长大,而且气泡成长周期很长,如图4所示。因此在研究气泡周围流场以及温度场对气泡破裂过程的影响时,忽略气膜生长过程及破裂后的气泡行为,假设在加热壁面上有一稳定气泡,根据数值计算结果分析气泡的稳定性。
三维稳态层流流动的连续性方程、动量方程和能量方程如下:

式中:ρ、cp、μ和λ分别是液体的密度、定压比热容、粘度和导热系数。V为速度矢量,T为温度,p为压力,g为重力加速度,j为竖直方向的单位矢量。自然对流的模拟采用Boussinesq模型:

式中:β为热膨胀系数,T0为参考温度,ρ0为参考密度。
在过冷沸腾中Marangoni效应是不能够被忽略的[9]。气泡周围液体存在的温度梯度导致气液界面上出现表面张力梯度。如图7,表面张力梯度在气液两侧均会产生切向应力,通常气相侧的剪切应力被忽略。则气泡边界的动力学边界条件可简化为

式中:dσ/dT是表面张力随温度变化的系数,∇sT是气液交界面上的温度梯度。

图7 气液界面切向受力示意图Fig.7 Schematic diagram of forces on a bubble surface in tangential direction
为与图3和图4中的实验条件接近,加热面和外边界分别设定为435 K和323 K的恒温壁面条件,其他部分都为绝热壁面条件。由于蒸发引起的液体流动相对于Marangoni对流引起的流动可以忽略[10],因此在数值模拟过程中,只考虑由蒸发冷凝造成的换热,不考虑其造成的传质流动。气液界面的热边界条件为第三类边界条件。其中假定气泡内为饱和蒸汽,且温度分布均匀;气液交界面上由蒸发冷凝引起的换热系数为

式中:hfg是相变潜热,ρv是蒸汽密度,Tv是气膜内气体温度是蒸汽相对分子质量,是气体常数,pv是蒸汽压力。为蒸发凝结系数,常压下对于水一般取0.03。因此,根据式(6)得出的气液界面的换热系数约为230 000 W/m2K。
能量和动量方程对流项的插值采用二阶迎风格式,压力速度耦合采取SIMPLE模型。

3 数值结果分析
加热面周边边界条件会影响气泡周围的Marangoni对流以及气泡顶部的冷凝过程,两者都可能会造成气液界面不稳定,进而导致气膜破裂,并形成气泡微细化沸腾现象[11-13]。

图8 50 K过冷度、62 K壁面过热度下气膜周围速度场Fig.8 Velocity field around vapor film at subcooling of 50 K and superheat of 62 K
图8所示为50 K过冷度62 K壁面过热度下,通过数值计算得出的齐平加热面和下沉加热面上气膜周围流体的速度矢量场。两种情况下气泡周围都存在Marangoni对流,但是对于加热面下沉的情况,气膜周围的Marangoni对流相对较弱。这主要是因为在加热面下沉形成的凹槽形区域,过冷水难以补充到加热面上,导致该区域液体温度较高,如图9所示。凹槽形区域温度梯度减小,使Marangoni对流的驱动力减小,气膜周围对流过程减弱。

式中:ρl为液体的密度,vm为气膜周围液体最大速度,h为气膜的高度,σ为液体的表面张力系数。当韦伯数超过临界韦伯数Wecr时,气泡将无法稳定存在,甚至发生碎裂[14]。Hinze[14]认为在粘性剪切流动中气泡破裂的临界韦伯数是1.18。Rigby等[15]在总结大量过去的研究结果之后,认为气泡破裂的临界韦伯数是1.2,因此,本文也以1.2作为临界韦伯数来判断加热面上气泡的稳定性。对于图7所对应的实验条件,下沉加热面时的韦伯数大约是0.71,而对于齐平加热面,韦伯数大约是2.84。由此可见,加热面下沉后,气膜会比较稳定、不易破裂。
当气泡顶部的冷凝很剧烈时,气液界面上会出现界面波动,并导致气膜破裂[12-13]。如图9所示,下沉加热面上气膜顶部液体的温度较高,其气液界面上的冷凝过程被削弱,导致可能引起气膜破裂的另一条件无法满足。
结合可视化实验和数值分析结果,可以看出,虽然加热面的位置仅仅略降低0.5 mm,加热面上的沸腾行为便极为不同,说明MEB现象对于加热面周围的边界条件极其敏感,也进一步表明,气膜周围的对流过程和冷凝过程很可能就是气膜无法稳定存在并发生碎裂的根本原因。

图9 50 K过冷度、62 K壁面过热度条件下,下沉加热面上气膜周围温度云图Fig.9 Temperature contour around vapor film at embedded heating surface with subcooling of 50 K and super-heat of 62 K
为分析气膜周围液体的流动对气膜稳定性的影响,引入表征流体惯性力和表面张力相对大小的韦伯数We。韦伯数定义为
4 结论
本文结合实验和数值分析,探究加热面边界条件对气泡微细化沸腾现象发生机理的影响,得到以下结论:
1)50 K过冷度下,加热面下沉约0.5 mm时,MEB现象不会发生;而在齐平加热面上,MEB现象却剧烈发生。
2)下沉加热面上气膜周围的Marangoni对流被减弱,导致韦伯数小于临界韦伯数。同时,气膜上部区域液体温度较高,气液界冷凝过程也被削弱。
3)气膜周围的对流过程,特别是Marangoni对流和气液界面上的冷凝过程很可能就是导致发生MEB时气膜破裂的主要原因。
[1]INADA S,MIYASAKA Y,IZUMI R,et al.Study of boiling characteristic curves in subcooled pool boiling of water[J].Bulletin of the JSME,1982,25(205):1085-1092.
[2]SUZUKI K,INAGAKI F,HONG C.Subcooled boiling in the ultrasonic field—on the cause of microbubble emission boiling[J].Heat Transfer Engineering,2011,32(7/8):673-682.
[3]TANGE M,TAKAGI S,WATANABE M,et al.Microbubble emission boiling in a microchannel and minichannel[J].Thermal Sciences Engineering,2004,12:23-29.
[4]SHOJI M,YOSHIHARA M.Burnout heat flux of water on a thin wire[C]//Proceedings of 28th National Heat Transfer Symposium of Japan.Fukuoka,Japan,1991:121-123.
[5]KUBO R,KUMAGAI S,UMEHARA N.Surface erosion caused by microbubble emission boiling[J].The Japan Society of Mechanical Engineers,1999,65(633):1731-1736.
[6]KUMAGAI S,KUBO R.Bubble motion in micro-bubble emission boiling[J].The Japan Society of Mechanical Engineers,1999,65(629):296-300.
[7]ZEIGARNIK Y A,PLATONOV D N,KHODAKOV K A,et al.Visualization of boiling of subcooled water[J].High Temperature,2011,49(4):566-570.
[8]ZEIGARNIK Y A,PLATONOV D N,KHODAKOV K A,et al.The nature of microbubble emission under subcooled water boiling[J].High Temperature,2012,50(3):78-83.
[9]MAREK R,STRAUB J.The origin of thermocapillary convection in subcooled nucleate pool boiling[J].Int.J.Heat Mass Transfer,2001,44:619-632.
[10]WANG Hao,CHRISTOPHER D M,PENG Xiaofeng.Jet flows from bubbles during subcooled pool boiling on microwires[J].Science in China Series E Engineering & Materials Science,2005,48(4):385-402.
[11]GLAZKOV V V,ZHILIN V G,ZEIGARNIK Yu A,et al.A study into development of instability and collapse of vapor layer on a heated solid hemispherical surface[J].High Temperature,2000,38(6):935-944.
[12]UENO I,ARIMA M.Behavior of vapor bubble in subcooled pool[J].International Journal for Microgravity Research and Applications,2007,19(3/4):128-129.
[13]UENO I,HATTORI Y,HOSOYA R.Condensation and collapse of vapor bubbles injected in subcooled pool[J].Microgravity Science and Technology,2011,23(1):73-77.
[14]HINZE J O.Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes[J].A I Ch E J,1955,1(3):289-295.
[15]RIGBY G D,EVANS G M,JAMESON G J.Bubble breakup from ventilated cavities in multiphase reactors[J].Chemical Engineering Science,1997,52(21/22):1677-3684.

