运动平台的磁性目标实时定位方法
于振涛,吕俊伟,许素芹,周静
(1.海军潜艇学院 航海观通系,山东青岛266001;2.海军航空工程学院控制工程系,山东 烟台 264001;3.海军92474部队,海南三亚572018)
磁性目标探测是根据武器装备等磁性目标的磁场特性进行探测、定位和识别的技术,航空磁探潜是磁性目标探测的一个重要军事应用[1-3]。目前磁性目标探测定位方法有磁场单分量定位方法、磁场三分量定位方法和磁场梯度张量定位方法等。近几年,磁梯度张量测量逐渐成为磁探技术的研究热点。美国、德国、澳大利亚等国家相继研制出一系列磁梯度张量探测仪器系统,并开展了航空探测试验[4-6]。与其他传统磁测方法相比,磁梯度张量测量有比较突出的优势,甚至被认为是磁法勘探的下一次突破[7]。
目前的磁梯度张量定位方法可以分为单测量点定位方法和多测量点定位方法。单测量点磁梯度张量定位方法是通过磁梯度张量值和目标磁场值解算出目标和测量系统的相对位置,其特点是定位速度快、定位精度高,可以实现基于单一测量点的磁性目标定位[8-10]。然而在磁梯度张量定位过程中测得的目标磁场不可避免地会受到地磁场和系统定向误差的影响,使得目标的探测定位难以实现[11-12]。基于运动平台的多测量点定位方法利用多空间点的磁梯度张量进行探测定位,可以弥补单测量点定位方法的不足,但是目前基于运动平台的定位方法需要求解非线性方程组,计算过程复杂,实时性不强[12-13]。
本文根据磁梯度张量定位原理,通过单点磁梯度张量定位算法的微分推导,提出了基于磁场三阶张量的目标定位算法,并结合运动平台探测定位静止磁性目标的特点,研究了磁梯度张量与磁场三阶张量的微分数学关系,提出了基于运动平台的磁性目标实时定位方法。该方法利用运动平台3个连续观测点的磁梯度张量值实现磁性目标的实时探测定位。最后通过仿真实验对该定位算法进行了验证,并对仿真结果进行了理论分析。
1 单点磁梯度张量定位原理
1.1 磁梯度张量
磁场是一个矢量场,其三分量Bx、By、Bz在空间3个方向的变化率即为磁梯度张量,包括9个要素,表达式为:

在没有空间电流密度的观测区域,磁场的散度和旋度都为0,即

因此磁梯度张量G矩阵具有对称性,即:
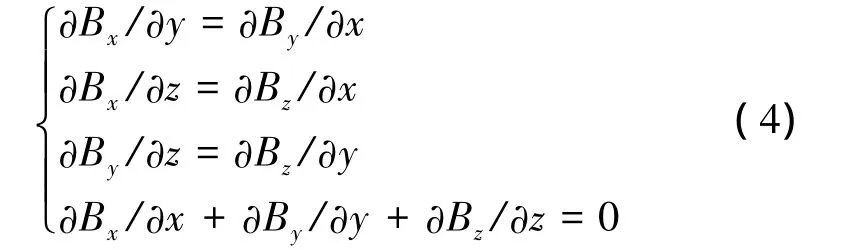
磁梯度张量中的9个要素有5个是独立的,因此只需要测量5个要素就可以得到磁梯度张量G。
1.2 磁梯度张量测量系统
目前磁梯度张量测量系统结构可以分为平面结构和空间结构,平面结构中的三角形结构为研究热点。三角形测量系统由3个3轴磁力仪组成,分别位于等边三角形的3个顶点,如图1所示。

图1 三角形磁梯度张量测量系统结构Fig.1 The triangle system of magnetic gradient tensor
根据差分方程,三角形测量系统的磁梯度张量计算公式如下

1.3 磁梯度张量定位算法
当探测距离大于2.5倍的磁性目标长度时,磁性目标可以视为一个磁偶极子[14-15]。在此条件下,距离磁性目标r处的磁场可以表示为[9]

式中:m为磁性目标的磁矩,μ0为真空磁导率,r=为测量点相对磁性目标的距离。
根据欧拉公式可以得到目标的位置信息与磁场矢量B和磁梯度张量G的线性关系[11]:

式(7)为单点磁梯度张量定位算法,已知单一观测点的目标磁场B和磁梯度张量G可实现磁性目标定位。在实际测量中会受地磁场的影响,由于地磁场的梯度比较小,一般小于0.02 nT/m,其远远小于磁性目标磁场的梯度张量,因此磁梯度张量的测量可以不受地磁场的影响。但地磁场会给目标磁场B的测量带来很大误差,导致单点磁梯度张量定位方法失效。
目前解决此问题的方法为:将式(6)代入式(7),得到磁梯度张量G与位置参数r的关系式:

然后利用多个测量点的磁梯度张量,构建关于位置参数的非线性定位方程组,并通过智能优化算法解算位置参数[12-13]。但此方法计算过程复杂,不能实现磁性目标的实时定位。
2 运动平台实时定位方法
2.1 磁场三阶张量定位算法
对单点磁梯度张量定位算法,式(7)求空间导数可得:

设

式中:T为磁梯度张量的空间导数,称为磁场三阶张量,式(10)可以表示为

式(12)为基于磁场三阶张量的磁性目标定位公式,即利用单点磁场三阶张量T和磁梯度张量G可以实现磁性目标的定位。
2.2 基于运动平台磁梯度张量仪的定位方法
当载体平台在平动条件下探测定位静止磁性目标时,设平台第i个采样位置点相对磁性目标的位置参数为ri,由于磁梯度张量G和磁场三阶张量T为位置参数r的函数,因此平台第i个采样位置点的磁梯度张量值和磁场三阶张量值可以表示为G(ri)和T(ri)。根据磁传感器的采样频率和载体平台的运动速度可知,对于常规探测距离满足平台采样间隔位移远远小于其相对目标的位移,即由于磁场三阶张量T(ri)为磁梯度张量G(ri)的空间导数,因此3个连续采样点存在以下关系式:

上式等式两边分别右点乘ri可得:

根据磁场三阶张量T的对称性,通过张量运算上式可以表示为

根据式(12)可知:

将式(16)代入式(15),得:

式(17)为基于运动平台磁梯度张量仪的磁性目标实时定位算法。式中G(ri-1)、G(ri)和G(ri+1)为磁梯度张量仪3个连续采样点的测量值;(ri+1-ri-1)为i-1 点到i+1 点的平台位移,(ri+1-ri-1)=2Δr,其值可以由平台的导航系统提供。当载体平台匀速平动时,采样间隔位移Δr为定值,定位式(17)可表示为

该定位算法利用载体平台的3个连续磁梯度张量测量值和载体平台的平动参数,可实时求出载体平台相对磁性目标的位置,进而实现对磁性目标的定位。目前基于磁梯度张量的目标定位方法为利用多测量点的磁梯度张量值,通过优化算法求解非线性方程组实现目标定位,此计算过程复杂,定位速度慢,实时性不强。而本文提出的实时定位方法计算过程简洁,不需要求解非线性方程组,可以实现磁性目标的实时探测定位。
3 仿真实验
仿真实验利用运动载体平台定位静止磁性目标,载体平台搭载磁梯度张量测量系统。设磁性目标位于空间直角坐标系的原点,以地理正东向为x轴,正北向为y轴,垂直向上为z轴。仿真实验初始条件为:磁性目标的磁矩m为(5×107,1×106,1×106)A·m2;载体平台在t0时刻的坐标为(-200,-200,100)m,平台采样频率为10 Hz,采样间隔位移Δr为(3,4,0)m,平台运动速度为 50 m/s;仿真实验采用平面三角形磁梯度张量测量系统,其中磁力仪的测量精度为0.01 nT,系统基线为0.5 m。仿真实验载体平台的运动过程如图2所示。
仿真流程如下:根据磁偶极子数学模型和载体平台的运动参数,仿真采样时刻点ti的平台磁梯度张量测量值G(ri)(采样时刻点ti对应的位置参数为ri);然后将3个连续采样点的仿真测量值G(ri-1)、G(ri)和G(ri+1)以及采样间隔位移 Δr代入定位式(18),求出时刻点ti的位置参数为ri,从而实现基于运动平台的磁性目标定位。

图2 仿真实验载体平台运动示意图Fig.2 The motion of vehicle platform in simulation experiment
3.1 探测定位仿真结果
图3为初始仿真条件下各时刻点的磁性目标探测定位误差。

图3 初始仿真条件下探测定位误差Fig.3 The localization error in original simulation condition
分析仿真结果可知,本文提出的运动平台实时定位方法对磁性目标有很好的定位效果,在400 m探测范围内,探测定位误差小于10 m;载体平台距离磁性目标越近,探测定位误差越小。
3.2 磁力仪测量精度对定位误差的影响

图4 不同磁力仪测量精度的磁定位误差Fig.4 The localization error of different magnetometer precision
图4为磁梯度张量测量系统中磁力仪测量精度分别为 0.1、0.01、0.001 nT 时,该实时定位方法计算得出的仿真结果。分析仿真结果可知,磁力仪的测量精度越高,实时定位方法对远距离磁性目标的定位误差越小;在3~5 s的时间段内,3个磁力仪精度都有很好的定位效果。
3.3 系统基线对定位误差的影响
图5为磁梯度张量测量系统基线分别为0.25、0.5、1 m时实时定位算法的探测定位仿真结果。由仿真结果可知,在3~5 s的时间段内,3个系统基线值都有很好的定位效果;但对于远距离磁性目标,系统基线越大探测定位效果越好。

图5 不同测量系统基线定位误差Fig.5 The localization error of different baseline intervals
4 仿真结果分析
以上仿真结果表明本文提出的磁梯度张量实时定位方法可以有效探测定位磁性目标,磁力仪精度和系统基线是影响远距离目标探测定位效果的主要因素。分析仿真实验结果可知,搭载磁梯度张量系统的运动平台探测水下大型磁性目标的典型距离为400 m,在此典型探测距离条件下,系统基线为0.5 m,磁力仪精度为0.1 nT。下面根据实时定位方法的基本原理对仿真结果进行理论分析。由式(6)得:

通过微分可以得到磁梯度张量的表达式:

通过理论计算各时刻点磁梯度张量和磁场三阶张量的Frobenius范数分别如图6和图7所示。
由运动平台实时定位方法的原理可知,目标定位效果与ti-1和ti+1时刻点磁梯度张量的差G(ri+1)-G(ri-1)直接相关,即磁场三阶张量的F范数越大该定位方法的定位效果越好。根据图7所示,各时刻点磁场三阶张量的F范数可知,在3~5 s的时间段内磁场三阶张量的F范数较大,这可以解释图3中3~5 s的时间段内定位效果较好的仿真结果。同理磁场三阶张量的F范数越大所需磁力仪的测量精度越低,因此图7也可以解释图4仿真结果中3~5 s的时间段内较低磁力仪精度也有较好定位效果的现象。

图6 各时刻点磁梯度张量的F范数Fig.6 The F norm of magnetic gradient tensor of time point

图7 各时刻点磁场三阶张量的F范数Fig.7 The F norm of magnetic third order tensor of each time point
当磁梯度张量测量系统中磁力仪的测量精度不变时,由测量系统的原理可知系统基线越小磁力仪间测量值的差越小,如果差值接近磁力仪的测量精度,磁梯度张量的测量将会有较大误差。由图7磁场三阶张量的F范数的变化可知,当测量系统距离磁性目标较远时磁场三阶张量较小,此时应选用较大的系统基线否则将会导致较大定位误差。以上分析可以解释图5仿真结果中较大系统基线对远距离磁性目标有较好定位效果的结论。
5 结束语
本文在磁梯度张量定位原理的基础上,通过研究磁性目标磁场梯度张量的空间导数,提出了基于磁场三阶张量的目标定位算法,并在此基础上建立了运动平台的实时定位方法。该定位方法计算过程简洁,不需要求解非线性方程组,可以实现磁性目标的实时定位。通过仿真实验对该定位方法进行了验证,结果表明该定位方法对磁性目标有很好的探测定位效果,不足之处在于对载体平台和磁性目标的运动状态都有要求,不适用于运动磁性目标的探测定位。在下一步的研究工作中需要在此方法的基础上研究运动磁性目标的探测定位技术。
[1]TAREK E T,AHMED S.Position detection of unexploded ordnance from airborne magnetic anomaly data using 3-D self organized feature map[J].International Symposium on Signal Processing and Information Technology,2005,23(1):322-327.
[2]HIROTA M,FURUSE T,EBANA K.Magnetic detection of a surface ship by an airborne LTS SQUID MAD[J].Transactions on Applied Superconductivity,2001, 11(1):884-887.
[3]张昌达.航空磁力梯度张量测量-航空磁测技术的最新进展[J].工程地球物理学报,2006,3(5):354-361.ZHANG Cangda.Airborne tensor magnetic gradiometry-the latest progress of airborne magnetometric technology[J].Chinese Journal of Engineering Geophysics,2006,3(5):354-361.
[4]STOLZ R,ZAKOSARENKO V,SCHULZ M,et al.Magnetic full-tensor SQUID gradiometer system for geophysical applications[J].Leading Edge(Tulsa,OK),2006,25(2):178-180.
[5]SMITH D V,BRACKEN R E.Field experiments with the tensor magnetic gradiometer system for UXO surveys:a case history[J].SEG Technical Program Expanded Abstracts,2004,23(1):806-809.
[6]GAMEY T J,DOLL W E,BEARD L P.Initial design and testing of a full-tensor airborne SQUID magnetometer for detection of unexploded ordnance[J].SEG Technical Program Expanded Abstracts,2004,23(1):798-801.
[7]吴招才,刘天佑.磁力梯度张量测量及应用[J].地质科技情报,2008,27(3):107-110.WU Zhaocai,LIU Tianyou.Magnetic gradient tensor:its properties and uses in geophysics[J].Geological Science and Technology Information,2008,27(3):107-110.
[8]于振涛,吕俊伟,张本涛.基于海底磁力仪阵列的磁性目标定位方法[J].武汉理工大学学报,2012,34(6):131-135.YU Zhentao,LYU Junwei,ZHANG Bentao.A method to localize magnetic target based on a seabed array of magnetometers[J].Journal of Wuhan University of Technology,2012,34(6):131-135.
[9]张朝阳,肖昌汉,阎辉.磁性目标的单点磁梯度张量定位方法[J].探测与控制学报,2009,31(4):44-48.ZHANG Chaoyang,XIAO Changhan,YAN Hui.Localization of a magnetic object based on magnetic gradient tensor at a single point[J].Journal of Detection & Control,2009,31(4):44-48.
[10]ORUC B.Location and depth estimation of point-dipole and line of dipoles using analytic signals of the magnetic gradient tensor and magnitude of vector components[J].Journal of Applied Geophysics,2010,70(1):27-37.
[11]TAKAAKI N,SATOSHI S,SHIGERU A.A closed form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J].IEEE Transactions on Magnetics,2006,42(10):3291-3293.
[12]张光,张英堂,李志宁,等.载体平动条件下的磁梯度张量定位方法[J].华中科技大学学报:自然科学版,2013,41(1):21-24.ZHANG Guang,ZHANG Yingtang,LI Zhining,et al.Localizing method of magnetic field gradient tensor under carriers moving parallelly[J].Journal of Huazhong University of Science& Technology:Natural Science Edition,2013,41(1):21-24.
[13]隗燕琳,肖昌汉,陈敬超,等.基于舰船矢量磁场的定位方法[J].上海交通大学学报,2009,43(8):1216-1221.WEI Yanlin,XIAO Changhan,CHEN Jingchao,et al.A new magnetic localization method based on vessel’s vectorial magnetic field[J].Journal of Shanghai Jiaotong University,2009,43(8):1216-1221.
[14]张朝阳,肖昌汉,高俊吉,等.磁性物体磁偶极子模型适用性的试验研究[J].应用基础与工程科学学报,2010,18(5):862-868.ZHANG Chaoyang,XIAO Changhan,GAO Junji,et al.Experiment research of magnetic dipole model applicability for a magnetic object[J].Journal Basic Science and Engineering,2010,18(5):862-868.
[15]吕俊伟,于振涛,樊利恒,等.舰船磁场模型适用范围研究[J].海军航空工程学院学报,2012,27(5):563-566.LU Junwei,LYU Zhentao,FAN Liheng,et al.Research on the applicability warship magnetic model[J].Journal Naval Aeronautical and Astronautical University,2012,27(5):563-566.

