基于三次Hermite插值的局部特征尺度分解方法

李　军，潘孟春

（1.国防科技大学　机电工程与自动化学院，长沙410082；2.空军驻长沙地区军事代表室，长沙410111）

基于三次Hermite插值的局部特征尺度分解方法

李军1，2，潘孟春1

（1.国防科技大学机电工程与自动化学院，长沙410082；2.空军驻长沙地区军事代表室，长沙410111）

内禀时间尺度分解（Intrinsic time-scale decomposition，简称ITD）方法采用线性变换获得基线信号，使得分解结果出现毛刺和瞬时频率失真现象。因此，在定义瞬时频率具有物理意义的内禀尺度分量（Intrinsic scale component，简称ISC）基础上，提出基于三次Hermite插值的局部特征尺度分解方法（Cubic Hermite interpolation-Local characteristicscale decomposition，简称CHLCD），该方法能够自适应地将一个复杂信号分解为若干个瞬时频率具有物理意义的内禀尺度分量之和。首先对CHLCD方法的原理进行分析，然后给出采用CHLCD对信号进行分解的详细步骤，最后采用仿真信号和滚动轴承信号对CHLCD进行验证，结果表明了CHLCD方法的有效性。

振动与波；局部特征尺度分解；三次Hermite插值；信号处理；故障诊断

傅里叶（Fourier）变换方法作为一种经典的信号处理方法，得到了大量的应用，但Fourier变换仅仅可以处理线性或者平稳信号，而实际中的大多数信号是非线性及非平稳的。针对Fourier变换方法的不足，时频分析得到了关注，由于其可以同时提供出非平稳信号在频域和时域的局部化信息，因此时频分析常被用来处理非线性信号问题。传统的时频分析有窗口Fourier变换、Wigner-Wille分布和小波变换，但上述方法都存在一定的缺陷，如窗口Fourier变换具有一定的时频窗口，Wigner-Wille分布有交叉项的干扰，而小波变换也需要小波基的选择，缺乏自适应［1］。因此，传统的信号分析方法在应用方面具有很大的局限性。

针对傅里叶变换和传统时频分析的不足，Mark G.Frei提出一种自适应的时频分析方法——内禀时间尺度分解（Intrinsic time-scale decomposition，简称ITD）方法［2］，该方法自适应地将非平稳的信号分解为若干固有旋转分量（Proper rotation component，简称PRC），且该分量的瞬时频率具有一定的物理意义。在文献［2］中将ITD方法和EMD方法进行对比，分析ITD方法在端点效应及计算速度上的优势，并且该方法克服了EMD方法的欠包络、过包络和LMD方法的信号突变等问题［3，4］。另外，由于ITD方法具有良好的非线性、非平稳信号分析能力，已在机械故障诊断领域得到了应用［5，6］。但是该方法还是存在一定的缺陷，没有对ITD方法及固有旋转分量的物理意义进行阐述，而且ITD方法中的基线是通过基于信号自身的一种线性变换得到，因此第二个单分量开始，得到的单分量和一般意义上的单分量不同，其信号具有明显的失真现象，从而得到的瞬时频率及瞬时幅值有较大的失真［7］。

由于ITD方法存在一些固有的缺陷，因此一些改进的ITD方法被提出。文献［8］采用三次样条代替线性变换来包络信号，文献［9］利用三次B样条插值代替线性变换包络信号，均解决了毛刺和频率失真问题。三次样条插值法具有收敛性好、光滑度高等特点，但三次样条插值会在包络过程中产生过包络或欠包络现象，尤其在具有冲击信息的强非平稳信号中更加明显。借鉴文献［8，9］的思想，本文拟将三次Hermite插值应用于ITD方法中，该方法具有保形特性，尤其适合于具有强非平稳特性信号的分析。因此结合标准三次Hermite插值和ITD方法的优点，提出一种基于三次Hermite插值的局部特征尺度分解方法（CubicHermiteinterpolation-Local characteristic-scale decomposition，简称CHLCD）。

1　基于Hermite插值的内禀时间尺度分解方法

标准三次Hermite插值法是一种工程中广泛应用的插值曲线构造方法，不仅具有三次样条插值法收敛性好，光滑度高的特点，相比于三次样条插值算法效率更高，且构造的曲线仅要求节点处一阶导数连续，在保证各点的连续性和平滑性的同时又具有优良的保形特性，不存在三次样条插值产生的过包络和欠包络现象，更适合于具有强非平稳特性的振动信号的包络拟合。

在ITD分解过程中，其均值曲线的定义是基于信号本身的线性变换，这导致从第二个分量开始，PRC分量信号就出现比较明显的失真（即能量有泄露），这也必然会影响分量间的正交性。在均值曲线的计算中，拟用标准三次Hermite插值代替线性变换，这样结合标准三次Hermite插值和TID的优势，不仅分解得到的分量没出现能量泄露现象，而且所得的分量有很好的光滑性。除此之外，借鉴文献［8］的思想，由于三次Hermite插值和三次样条插值在ITD方法中的应用具有一定的相似性，因此可以把文献［8］中定义瞬时频率具有物理意义的单分量信号所需条件引入到本文中。

1.1 ITD方法

ITD方法能将待分解的非线性信号分解为若干PRC及一个趋势项分量。设Xt为待分解的信号，分解之前先定义基线的提取算子L，从而使得从原信号中去除该基线信号后的余量成为第一个PRC。一次分解的表达式为［8］

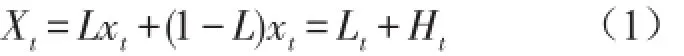
式中假设在［0，τk］上定义了Lt和Ht，而Xt在［0，τk+2］上有定义。在连续极值点［τk，τk+2］区间上定义Xt的基线信号提取算子L，即

式中a是分解时的增益控制参数，0＜a＜1；Lt保留信号在每个极值点处的单调性，Ht提取每个极值点间叠加的局部高频单分量信号—固有旋转分量。因此，重复上述分解过程就可以得到若干PRC及单调趋势项信号。

1.2 CHLCD算法

虽然ITD克服了EMD和LMD中的一些缺陷，但是文献［2］中并没有对ITD方法及PRC的物理意义做出阐述；另外，由式（2）可知，ITD算法本身是通过线性变换的方法获取基线信号，得到的信号波形显示毛刺现象而失真。因此，论文借鉴文献［8］中局部特征尺度分解方法的思想，在阐述ITD分解方法的物理意义基础之上对ITD方法进行一定的改进。

在ITD分解时，对于较为理想的PRC，其如式（2）所表示的基线分量在所有区间［τk，τk+2］中都应该为零，式（3）所示的Lk+1也应该为零。因此，ITD方法对原信号分解获到的PRC应满足基线分量控制点Lk+1为零。在此基础之上定义具有物理含义的分量—内禀尺度分量（Intrinsic scale component，简称ISC）。所示的ISC分量满足以下条件：

（1）在所有数据段之内，任意相邻两个极值点的符号互异。

（2）在所有数据段之内，数据波形的极值点是Xk，（k=1，2，∙∙∙，M），每个极值点所对应时刻是τk，（k=1，2，…，M），由两个任意极大或者极小值点（τk，Xk）、（τk+2，Xk+2）连接而成的数据段在其中间位置极大或者极小值点（τk+1，Xk+1）所对应的时刻τk+1函数值和该极大（小）值Xk+1之间的比值保持不变，即可以满足

上述的两个条件能保证ISC分量两个任意相邻的极值点间有单一模态，且在极值点和相邻零交叉点间近似符合标准的正弦曲线图形，因此其瞬时频率有一定的物理意义。

CHLCD算法是假设任意复杂的信号是不同ISC分量组合而成，任何两个ISC分量间是相互独立的，这样就能将该复杂的信号分解成若干个ISC分量，其具体的步骤方法如下：

①确定X（t）所有的极值点Xk，（k=1，2，∙∙∙，M）和其所对应时刻τk，（k=1，2，…，M），并且设置好参数a，接着计算每个基线信号控制点Lk，即式（3）；然后对所有Lk进行三次Hermite插值，能获得基线信号L1。

②将L1从原信号中进行分离，即一次插值获得的信号另保存为P1。可以认为P1是一个ISC分量，则P1为信号x（t）的第1个单分量。另外，理想的ISC分量必须满足Lk+1为零，实际上可以设置变动量Δ，当||Lk+1≤Δ时迭代终止。

③如获得的信号P1不满足上述ISC条件，就会将P1作为原信号重复上述步骤①和②，再循环k次，直到获得单分量Pk，并且分量Pk满足ISC的条件，即为信号x（t）的第1个分量ISC1。

④将ISC1从x（t）中进行分离，剩下的则成为一个全新的信号r1，将r1视为原信号重复上述步骤①、②和③，获得x（t）的第二个满足ISC条件的单分量ISC2。重复步骤循环n次，可以得到信号x（t）的n个满足ISC条件的单分量，直至rn是一单调性函数结束。这样就可以将x（t）分解为n个ISC和一个单调性函数rn之和，即

2　仿真信号分析

考察如式（5）所示的仿真信号

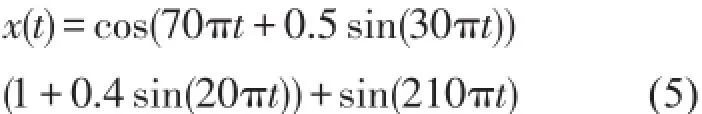
x（t）由一个调幅调频分量和一个正弦分量组成。如图1所示。

图1仿真信号时域波形图

图2为待分析信号的FFT频谱和信号功率谱。为比较分解效果，在端点效应处理后采用ITD和CHLCD方法对其进行分解。其中端点效应处理方法都采用G Rilling提出的镜像对称延拓方法［10］。首先将信号通过端点延拓处理，接着采用ITD和CHLCD方法分别对延拓后的信号进行分解，得到单分量信号，如图3和图4所示。两种方法都可以将各单分量成分分解出来，但是ITD分解的结果呈现出明显的毛刺现象，使得信号失真；CHLCD分解的结果较为光滑，避免了出现毛刺现象。

图2　仿真信号FFT频谱和信号功率谱

图3　 ITD分解结果

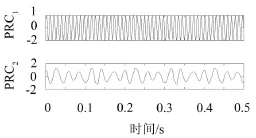
图4　 CHLCD分解结果

从以上分解结果可知，两种方法都可以把各单分量分解出来，下面再从两个分量的瞬时频率和瞬时幅值加以分析，结果分别如图5和图6所示。图5和图6所求得的瞬时特征信息中，比较第1个分量的瞬时包络幅值和瞬时频率，ITD和CHLCD方法的结果很接近，效果都比较好，但是ISC1的效果也明显优于PRC1；比较第2个分量可以发现，无论是瞬时频率还是瞬时包络幅值，ISC2的效果都比PRC2的更准确，波动性更小，而且差别更加明显。因此，说明CHLCD是一种有效可行的分解方法。

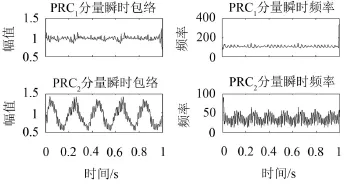
图5　 ITD分解单分量的瞬时包络幅值和瞬时频率

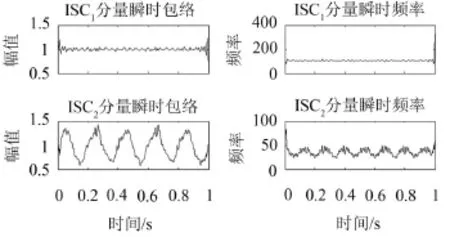
图6　 CHLCD分解单分量的瞬时包络幅值和瞬时频率

分析单分量信号的瞬时包络幅值和瞬时频率后，然后再通过Hilbert谱和边际谱来比较分析，经过上述几种分解方法分解后进行Hilbert变换，得到的Hilbert-Huang时频图如图7—图8所示。由于ITD分解采用线性变换，得到的Hilbert谱出现较大失真，使相应的时频谱图失去了原有的物理意义，无法准确地反映出原信号的瞬时幅值和随时间变化的频率规律；CHLCD得到的Hilbert时频图很好地反映了原信号的基本信息，没有出现较大偏差。图9—图10为两种方法的边际谱，ITD中心频率处出现较多虚假成分，而CHLCD方法得到的边际谱明显改善不少。因此，CHLCD分解方法和其它分解方法相比具有明显的优越性。

综上所述，从各方面比较两种方法的效果，在时域图方面，CHLCD没有出现毛刺，解决了ITD毛刺问题；分量瞬时幅值和频率方面，CHLCD改善了ITD方法的瞬时频率和瞬时幅值失真问题，具有较好的效果；从Hilbert-Huang时频图和边际谱方面，CHLCD分解分量的频率更加集中，能准确地反映出原信号的瞬时幅值和随时间变化的频率规律。因此，从各方面都证明了CHLCD方法比ITD方法更具优越性。

图7　 ITD分解得到的Hilbert-Huang时频图

图8　 CHLCD分解得到的Hilbert-Huang时频图

图9　 ITD分解得到的边际谱

图10　 CHLCD分解得到的边际谱

3　实例应用

为验证CHLCD方法的有效性，将该方法应用到滚动轴承的故障诊断中。在滚动轴承发生机构损伤时，其运行的过程中会出现周期性的冲击，同时激发轴承中元件的固有频率，从而导致高频衰减振动，其中高频衰减的振动幅值会被周期冲击振动所调制。因此，为了更好的提取滚动轴承相应的故障特征，需要对轴承的故障振动信号进行解调分析。包络解调方法是一种基于Hilbert变换的解调分析方法，可以对轴承的故障振动信号进行解调分析，得到相应的故障特征信息，因此将CHLCD方法与包络解调相结合应用到滚动轴承的故障诊断中。

为验证上述方法的有效性，选用美国凯撒西储大学电气工程实验室公开的轴承数据。采样频率为12 kHz，转速为1 797 r/min，负载为0 HP，故障点的直径为0.177 8 mm，故障深度为0.279 4 mm。计算的转频fr≈29.95Hz，外圈故障特征频率fo≈107.3 Hz，内圈故障特征频率fi≈166.4Hz。

首先任意选择一个具有外圈故障的振动加速度信号，其时域图如图11所示，用CHLCD方法对原始振动信号分解，得到的分量图如图12所示。

图11　外圈故障状态信号时域图

图12　外圈故障信号CHLCD分解后的分量

滚动轴承在发生故障时，其故障特征往往集中在高频部分，因此选取CHLCD分解的前两个分量作Hilbert解调分析，得到其包络信号，然后对包络信号进行谱分析得到其包络谱。图13和图14分别为前两个分量的包络谱。

图13　外圈故障第一个分量包络谱

图14　外圈故障第二个分量包络谱

从图13和图14分量的包络谱中可以看出，在故障频率fo及其倍频处出现明显峰值，验证了此时轴承的外圈出现故障。

为进一步验证该方法的有效性，再任意选取一个具有内圈故障的振动加速度信号，其时域图如图15所示，经过CHLCD分解后得到的分量时域图如图16所示。

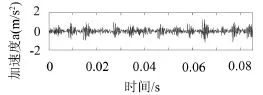
图15　内圈故障状态信号时域图

图16　内圈故障信号CHLCD分解后的分量

同样选择其分解得到的前两个分量作Hilbert变换，然后得到相应的包络谱如图17和图18所示。

图17　内圈故障第一个分量包络谱

从图17和图18分量的包络谱中可以看出，在故障频率fi及其倍频处出现明显峰值，验证了此时轴承的内圈出现故障。

图18　内圈故障第二个分量包络谱

4　结语

本文在ITD的基础上，结合标准三次Hermite插值的优点，提出一种基于三次Hermite插值的特征

尺度分解方法（CHLCD），并给出该方法对信号进行分解的详细步骤。对CHLCD方法和ITD方法进行对比分析，从多个层面比较两种分解方法，结果表明CHLCD方法能够改善ITD方法分解得到的分量出现波形失真的缺点。

［1］程军圣，张亢，杨宇，等.局部均值分解与经验模态分解的对比研究［J］.振动与冲击，2009，28（5）：13-16.

［2］Frei M G，Osorio I.Intrinsic time-scale decomposition: Time-frequency-energy analysis and real-time filtering of non-stationary signals［J］.Proceedings of the Royal Society，A，2007，463:321-342.

［3］Cheng Junsheng，Yu Dejie，Yang Yu.Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform［J］.Mechanical Systems and Signal Processing，2007，21（3）:1197-1211.

［4］Cheng Junsheng，Zhang Kang，Yang Yu，et al.Comparison between the methods of local mean decomposition and empirical mode decomposition［J］.Journal of Vibration

［5］胥永刚，谢志聪，崔玲丽，等.基于ITD的齿轮磁记忆信号特征提取方法的研究［J］.仪器仪表学报，2013，34（3）：671-676.

［6］裴峻峰，陈园丽，代云聪，等.基于ITD和灰色关联度的轴承故障诊断方法［J］.2014，（2）：48-51.

［7］程军圣，郑近德，杨宇.一种新的非平稳信号分析方法—局部特征尺度分解［J］.振动工程学报，2012，25（2）：215-220.

［8］程军圣，杨怡，杨宇.局部特征尺度分解方法及其在齿轮故障诊断中的应用［J］.机械工程学报，2012，48（9）：64-71.

［9］钟先友，曾良才，赵春华，等.基于BITD和同态滤波解调的齿轮故障诊断方法［J］.中国机械工程，2013，20：2775-2780.

［10］Rilling G，Flandrin P，Goncalves P.On empirical mode decomposition and its algorithms［C］.Proceedings of IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03，Grado，Italy，2003.

Local Characteristic-scale Decomposition Method Based on Cubic Hermite Interpolation

LIJun1，2，PAN Meng-chun1
（1.College of Mechatronics Engineering andAutomation，National University of Defense Technology，Changsha 410082，China；2.Air Force Military Representative Office in Changsha，Changsha 410082，China）

Since linear transformation is used to obtain baseline signal in intrinsic time scale decomposition（ITD）method，burr and instantaneous frequency distortion will appear in the decomposition results.Therefore，a rational Cubic Hermite interpolation—Local characteristic-scale decomposition（CHLCD）method is presented.In this method，any complex signal can be adaptively decomposed into a sum of several independent rational intrinsic scale components（ISCs），whose instantaneous frequencies have obvious physical meanings.Firstly，the principle of the CHLCD method was analyzed.Then，the detailed steps of CHLCD of signal were given.Finally，a simulation signal was adopted to verify the CHLCD method.Experimental results show that the CHLCD method can effectively decompose signals.

vibration and wave；local characteristic-scale decomposition；cubic Hermite interpolation；signal processing；fault diagnosis

TH113

ADOI编码：10.3969/j.issn.1006-1335.2015.05.033

1006-1355（2015）05-0159-05+175

2015－03－30

李军（1984－），男，硕士研究生。E-mail:pansea1989@163.com

潘孟春（1963－），男，教授。