风力机叶片挥舞—摆振气弹稳定性分析

李　亮，李映辉，杨鄂川，3

（1.安徽理工大学　理学院力学系，安徽　淮南232001；2.西南交通大学　力学与工程学院，成都610031；3.重庆理工大学　车辆工程学院，重庆400054）

风力机叶片挥舞
—摆振气弹稳定性分析

李亮1，李映辉2，杨鄂川2，3

（1.安徽理工大学理学院力学系，安徽淮南232001；2.西南交通大学力学与工程学院，成都610031；3.重庆理工大学车辆工程学院，重庆400054）

根据Euler-Bernoulli梁理论和粘弹性材料的Kelvin-Voigt理论建立风力机叶片挥舞—摆振耦合非线性动力学方程。将位移视为静态位移和动态位移的叠加，进而将非线性动力学方程线性化为动态位移的线性方程，得到叶片耦合振动特征方程。使用基于加权残值的Galerkin方法求解特征方程，分析叶片气弹稳定性，讨论风速、安装角、耦合效应和材料阻尼对叶片颤振稳定性和非线性自激振动行为的影响。结果表明：摆振方向易出现不稳定振动，通过设置安装角，利用挥舞—摆振耦合可以控制不稳定振动，但当安装角太大时，挥舞—摆振耦合会引起不稳定振动。

振动与波；风力机叶片；气弹稳定性；颤振；自激振动

风力机运转过程中，气动力、弹性力和惯性力相互耦合，易引起叶片不稳定振动。已有对气弹稳定性的研究多基于叶片翼型截面模型：林学海和任勇生［1，2］采用ONERA气动力模型对叶片挥舞—摆振动力失速稳定性进行分析，讨论叶片刚度、锥角、结构阻尼等因素对气弹稳定性的影响；刘廷瑞等［3］基于Beddoes-Leishman气动力模型，使用拟合气弹系数的方法简化计算，研究了叶片动力失速稳定性；王伟等［4］建立叶片三维叶型模型和风力机整机模型，采用振型叠加法研究叶片颤振稳定性，讨论叶片结构参数对颤振稳定性的影响。为获得较高的风能利用率，叶片通常设计为变翼型结构。因此，相对于翼型截面模型，连续系统模型能够更好地描述叶片整体结构特征：虞心田和崔尔杰［5］建立叶片挥舞—扭转耦合动力学方程，然后将连续模型简化为等效的刚体模型，研究叶片的颤振边界问题；李本立和安玉华［6］考虑叶片挥舞—摆振—扭转耦合非线性振动，使用模态法求解微分方程，分析叶片气弹稳定性；任勇生和张明辉［7］基于叶片挥舞—摆振—扭转耦合振动偏微分方程和扩展的Theodorsen气动力模型，使用Galerkin法研究均匀叶片气弹稳定性问题，分析弯曲刚度、扭转刚度、预锥角等因素对气弹稳定性的影响。

本文研究变截面叶片挥舞—摆振气弹稳定性，讨论挥舞—摆振耦合、材料阻尼等已有研究较少考虑的因素对颤振稳定性的影响。为考虑非线性影响，将位移分解为静态位移和动态位移，进而将非线性方程线性化为动态位移的线性方程，得到叶片振动特征方程，使用Galerkin方法分析叶片振动特性，讨论叶片颤振稳定性和自激振动行为。

1　动力学方程

叶片构型如图1所示，摆振为旋转平面内的弯曲，挥舞为垂直于旋转平面的弯曲。旋转坐标系（xyz）用来描述叶片变形，其原点在叶根截面剪切中心，x轴沿弹性轴指向叶尖，y轴沿摆振方向，z轴沿挥舞方向。扭角θ=θ0+θt是弦线与旋转平面的夹角，θ0是安装角，θt=θt（x）是截面预扭角。e是叶根到轮毂中心的偏置量，ex和ey是其沿x轴、y轴的分量。假设叶片截面质心、形心和剪切中心三者重合，将细长叶片简化为Euler-Bernoulli型悬臂梁，考虑其弯弯耦合振动，在弹性梁模型［6-8］的基础上，通过Kelvin-Voigt理论（σ=Eε+ηdε/dt，σ为应力，E为杨氏模量，ε为应变，η为粘性系数）引入材料阻尼，得到动力学方程。

图1　叶片构型及坐标系

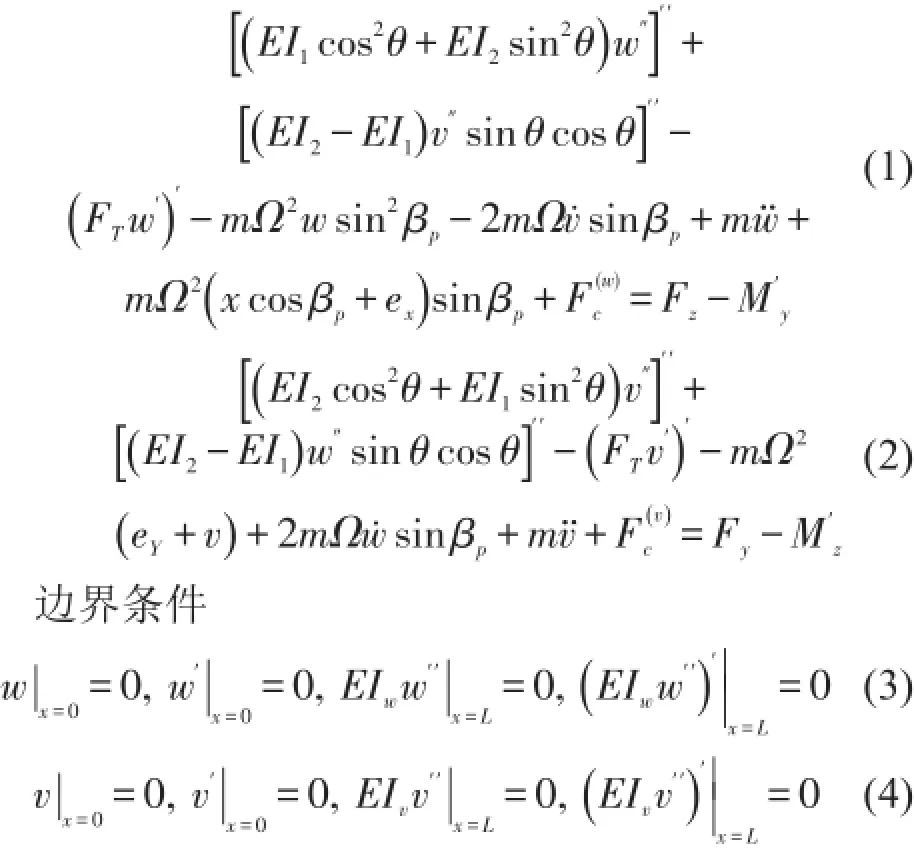
其中EI1=EI1（x）和EI2=EI2（x）是第一、第二弯曲刚度，EIw=EIw（x）和EIv=EIv（x）分别是挥舞、摆振刚度，近似表示为

w和v分别是挥舞和摆振位移，撇和点分别表示对x和t求导，FT=∫AEεdA是轴力∫AσdA的弹性部分，A=A（x）是截面面积，m=m（x）是单位长度的质量，Ω是叶片旋转角速度，βp是锥角，L是叶片长度，和是材料阻尼力，其表达式如下

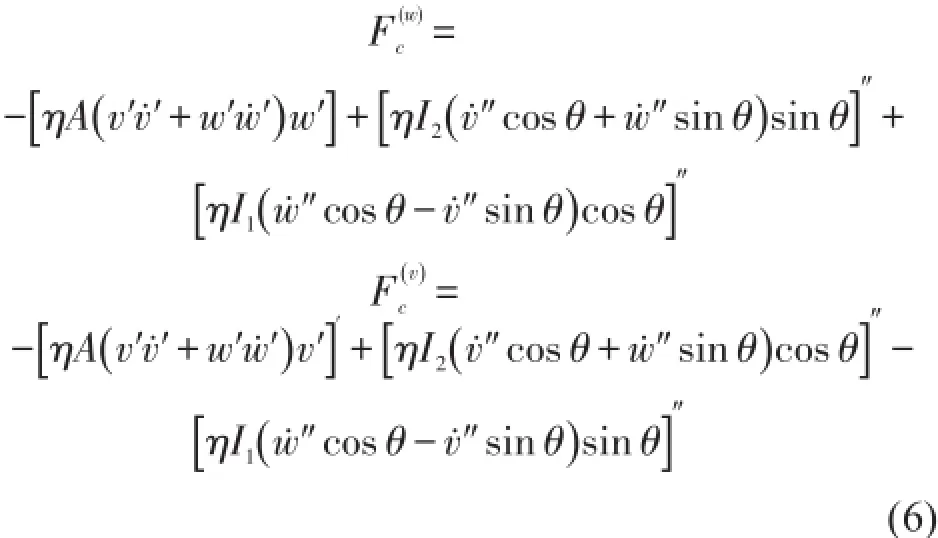
（Fy，Fz）和（My，Mz）分别是沿（y，z）轴的分布力和力矩，气动力和重力可作为分布荷载加入方程（1）—（2）右端。选用文献［6］给出的非定常气动力模型，其表达式如下式中ρ为空气密度，a为升力曲线斜率，c=c（x）为弦长，R为旋转半径，λ为入流速度比，其表达式

v0为轮毂处的风速，λ0=v0/（ΩR）为轮毂处的入流速度比

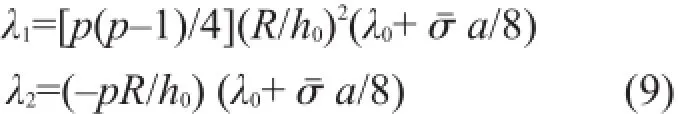
为转子实度，nb为叶片数，CDO为阻力系数，rx=rx（x）是截面x的径向位置，eA=eA（x）为气动中心到剪切中心的偏置量（气动中心在前时为正）。重力表达式

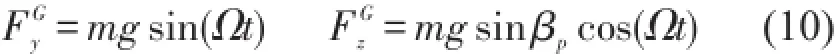
式中g为重力加速度。

2　非定常气动力作用下叶片自由振动特性

将位移看作静态位移κs与动态位移κd（κ=w，v）的叠加

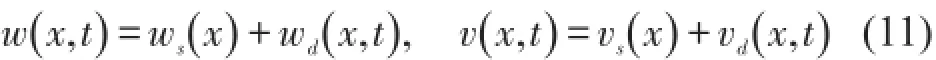
将式（8）代入方程（1）—（2），得静态位移方程

方程组（9）为关于x的4阶非线性变系数常微分方程组，其解可由数值方法（如Euler方法、Runge-Kutta法）求出。动态位移满足非线性偏微分方程组

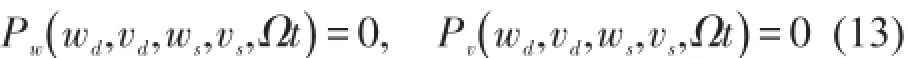
先讨论自由振动特性，在（10）中去掉强迫项和动态位移的非线性项，得到如下线性偏微分方程组

将动态位移分离变量

式中ω为复数频率，其实部为固有频率，虚部为阻尼系数，γ为模态函数。将式（12）代入式（11），约掉时间项，可得特征方程：

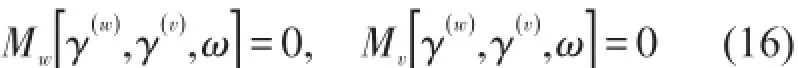
式（13）为4阶变系数常微分方程组，其精确解无法直接求出，本文采用基于加权残值的Galerkin法［7，9］求解。将模态函数表示为满足边界条件且线性无关的试函数的线性组合

其中，Nw和Nv分别表示所选挥舞和摆振试函数的个数。将（14）代入（13），然后在方程Mμ=0两端同乘）后对x从0到L积分，得到如下代数方程组

式中M和K是正定的质量和刚度阵，C是阻尼阵，T是矩阵转置，0（Nw+Nv）×1是（Nw+Nv）×1零矩阵。系数a1，···，aNw，b1，···，bNv不能同时为零，所以矩阵-ω2M+ iωC+K非满秩，即有

由方程（14）-（16）可求出复数频率ω和模态函数，阻尼比ζ=Im（ω）/［2Re（ω）］。当ζ为负数时，叶片出现自激振动和发散不稳定。

3　非定常气动力作用下叶片非线性自激振动

叶片动能主要集中在前两阶模态（第1阶挥舞和第1阶摆振模态）［10］，使用Galerkin方法对连续系统1阶截断，设

式中γf和γl分别是挥舞和摆振第1阶模态函数，qf和ql是广义位移（其对时间的一、二次导分别为广义速度和广义加速度）。将（17）代入方程（1）-（2）得离散系统

式（18）为非线性常微分方程组，为讨论叶片非线性自激振动，在（18）中去掉周期外激励，得

式（19）可由数值方法［11-12］或摄动理论进行求解，本文采用数值积分求解。

4　数值结果

选取某MW级风力机叶片为计算模型，叶片长度L=48 m，杨氏模量E=30 GPa，气动中心到弹性轴距离eA=c/4，叶片密度ρb=1.8×103kg/m3，轮毂高度h0=2 L，锥角βp=2°，偏置量ex=2 m，ey=0 m，其它分布参数见图2。空气密度ρ=1.25 kg/m3，升力曲线斜率a=2 π，阻力系数CDO=0.016，风速梯度常数p=0.167，转速Ω=15 r/min。使用4阶Runge-Kutta法求解静态位移方程，采用Galerkin法求解特征方程，其中挥舞、摆振试函数均选取为｛（x/L）2，···，（x/L）9｝。

图3给出了挥舞、摆振第1阶阻尼比随安装角的变化。若忽略挥舞—摆振耦合效应，则挥舞阻尼比随安装角绝对值的增大而减小，这是因为截面扭角对挥舞频率影响较大，频率随安装角幅值的增大而增大，但安装角对挥舞阻尼系数影响相对较小。由于预扭角的存在，挥舞最大阻尼比出现在-10°附近。安装角对摆振阻尼系数影响较大，阻尼系数随安装角增加而增大，但安装角对摆振频率影响较小，因此摆振阻尼比随安装角的增大而增大。忽略耦合效应的结果显示：安装角为负（逆时针旋转的叶片，前缘在旋转面前面时为负）且幅值较大时，摆振方向易出现气弹性不稳定性。

考虑挥舞—摆振耦合效应影响，由于安装角和截面预扭角的存在，摆振方向的能量传递到挥舞方向，挥舞阻尼较大，在幅值较大的负安装角时出现的摆振不稳定性被控制。当风速较低时（如v0=8 m/s），挥舞阻尼比变化趋势与忽略耦合效应时相同。当风速较高时（如v0=32 m/s），挥舞阻尼比随安装角增大而增大，当安装角为正且幅值较大时，摆振方向出现不稳定振动。两种情况（忽略和考虑耦合效应）的对比结果显示：通过设置安装角，利用挥舞—摆振耦合能改进叶片气弹稳定性，但当安装角很大时，耦合效应反而会引起气弹不稳定振动。

图2　叶片几何和物理参数

图3阻尼比随安装角的变化

图4—图8揭示叶片非线性自由振动行为，计算时选取风速v0=32 m/s，图4—图7不考虑材料阻尼。气弹不稳定性出现在摆振方向（见图3），因此只考虑摆振响应。图4给出安装角-2°时，忽略耦合效应的摆振相图，初始值选取为［10-50］，结果显示摆振响应出现发散不稳定现象，响应幅值随时间逐渐增大。图5给出安装角20°时，忽略耦合因素的摆振相图，此时叶片运动稳定，摆振响应随时间逐渐收敛于稳定的平衡点。图6给出安装角-2°时，考虑耦合效应的摆振相图，系统运动稳定，摆振相轨迹收敛到稳定的平衡点，图4中出现的发散不稳定通过耦合效应被控制。图7给出安装角20°时，考虑耦合效应的摆振相轨迹，同图5相比，耦合效应使系统运动行为发生变化，摆振响应由稳定的平衡点变成大幅值的拟周期运动。图4—图7验证了图3的结论。图8给出安装角20°时，考虑耦合效应的摆振响应随材料阻尼的分岔图，结果显示摆振响应随材料阻尼的增大由大幅值的拟周期运动变为稳定的平衡点，因此材料阻尼改善了叶片气弹稳定性。

图4　忽略耦合的摆振相轨迹（θ0=-2°）

5　结语

图5　忽略耦合的摆振相轨迹（θ0=20°）

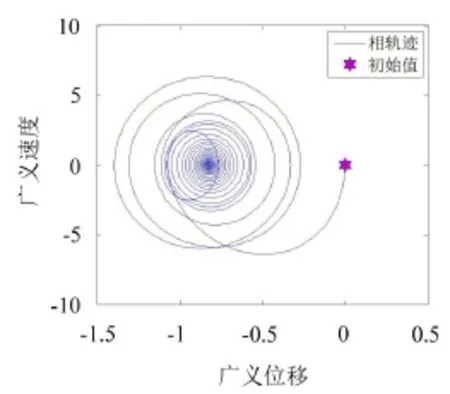
图6　考虑耦合时摆振相轨迹（θ0=-2°）

基于Euler-Bernoulli梁模型和Galerkin法分析叶片气弹稳定性，结果表明：通过设置安装角，利用挥舞—摆振耦合效应可以改善叶片气弹稳定性，但当安装角太大时，耦合效应反而引起叶片不稳定振动；材料阻尼可以改善叶片气弹稳定性。

图7　考虑耦合时摆振时间历程和庞加莱映射（θ0=20°）

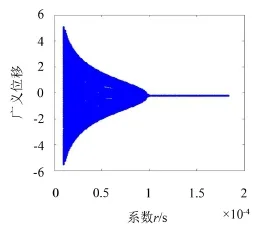
图8　摆振位移对r=η/E的分岔图

［1］林学海，任勇生.基于ONERA气动力模型的风力机叶片颤振时域分析［J］.山东科技大学学报（自然科学版），2009，28（3）：56-60.

［2］任勇生，林学海.风力机叶片挥舞/摆振的动力失速非线性气弹稳定性研究［J］.振动与冲击，2010，29（1）：121-124.

［3］刘廷瑞，任勇生，杨兴华.基于气弹系数的气弹稳定性分析［J］.太阳能学报，2010，31（4）：513-516.

［4］王伟，廖明夫，Martin Kühn.风力机叶片三维模型颤振问题［J］.噪声与振动控制，2013，33（5）：90-96.

［5］虞心田，崔尔杰.分析水平轴风力机叶片气弹性稳定性的简单方法［J］.太阳能学报，1990，11（1）：52-59.

［6］李本立，安玉华.风力机气动弹性稳定性的研究［J］.太阳能学报，1996，17（4）：314-320.

［7］任勇生，张明辉.水平轴风力机叶片的弯扭耦合气弹稳定性研究［J］.振动与冲击，2010，29（7）：196-200.

［8］Li L，Li Y H，Lv H W，et al.Flapwise dynamic response of a wind turbine blade in super-harmonic resonance［J］. Journal of Sound and Vibration，2012，331（17）:4025-4044.

［9］李映辉，李中华.超音速下粘弹性夹层壁板颤振分析［J］.力学季刊，2012，33（3）：449-455.

［10］Jørgensen K H，Nielsen S R K.System reduction in multibody dynamics of wind turbines［J］.Multibody System Dynamics，2009，21:147-165.

［11］吕海炜，李映辉，李中华，等.超声气流下粘弹性夹层壁板非线性颤振分析［J］.航天器环境工程，2013，30（1）：40-48.

［12］覃文源，张志谊，华宏星.摩擦力作用下推进轴系弯—扭耦合振动特性分析［J］.噪声与振动控制，2013，33（5）：4-9.

Flap/Lead-lagAeroelastic Stability Analysis for Wind Turbine Blades

LI Liang1，LI Ying-hui2，YANG E-chuan2，3
（1.Department of Mechanics，College of Science，Anhui University of Science and Technology，Huainan 232001，Anhui China；2.School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu 610031，China；3.ChongqingAutomobile Institute，Chongqing University of Technology，Chongqing 400054，China）

The nonlinear partial differential equations which govern the coupled flap-lead/lag vibration of wind turbine blades were established based on the Euler-Bernoulli beam theory and the Kelvin-Voigt theory for cohesive elastic composite materials.By decomposing blade displacement into static displacement and dynamic displacement，the nonlinear governing equations were linearized to the linear equations for the dynamic displacement.And then，the characteristic equation of the coupled vibration was obtained.The Galerkin method based on the method of weighted residuals was employed to solve the characteristic equation and analyze the aeroelastic stability of the blades.The influence of wind speed，installation angle，coupling effect and material damping on the aeroelastic stability and nonlinear self-excited oscillation of the blades was discussed.Results show that the coupling effect between flap and lead-lag may be employed to improve the aeroelastic stability of the blades，but very strong coupling effect between them due to the large installation angle may bring about vibration instability.

vibration and wave；wind turbine blade；aeroelastic stability；flutter；self-excited oscillation

O317；O322；O323

ADOI编码：10.3969/j.issn.1006-1335.2015.05.005

1006-1355（2015）05-0030-05

2014－12－16

国家自然科学基金项目（11072204，11372257）；中央高校专项基金（SWJTU11ZT15）；2013年四川省青年科技创新团队项目；上海市力学在能源工程中的应用重点实验室资助项目；教育部留学回国人员科研启动基金项目（2012-42）；安徽省自然科学基金项目（1308085MA13）

李亮（1984－），男，山东省曲阜市人，讲师，目前从事非线性动力学研究。

E-mail:lli@my.swjtu.edu.cn