微机械谐振器可变锚点结构能量耗散特性分析

张　厦，张文明

（上海交通大学　机械系统与振动国家重点实验室，上海200240）

微机械谐振器可变锚点结构能量耗散特性分析

张厦1，张文明2

（上海交通大学机械系统与振动国家重点实验室，上海200240）

微机械谐振器在振动过程中总会产生能量耗散，并且具有诸如空气阻尼耗散、热弹性阻尼耗散、锚点结构耗散、表面耗散等诸多耗散机制，其中锚点结构耗散是一种主要的能量耗散机制。应用完美匹配层方法，将无限大区域入射波的吸收问题转化到有限区域内进行。针对中心支撑圆盘体模态谐振器，设计两种不同的锚点支撑结构，并分别讨论其几何结构的变化对谐振器固有频率和锚点损耗品质因子的影响。结果证明通过调整锚点结构，可以大幅度提高谐振器的锚点耗散品质因子，提高能量的利用效率。

振动与波；微机械谐振器；锚点耗散；完美匹配层；结构优化

锚点结构能量耗散［1］又可以称作支撑结构能量耗散，是微机电系统［2］（Micro-Electro-Mechanical System，MEMS）中主要的能量耗散机制之一。对于微机械谐振器来说，锚点结构耗散的能量是通过谐振体与支撑结构相互耦合而耗散掉的机械能。当弹性谐振体振动时，会在其固支端产生振动剪切力和弯矩，随后作为激励源在基底上激发出弹性波，并通过基底传播到无穷远处耗散掉，即支撑结构吸收了谐振器的部分振动能量。

锚点结构能量耗散被认为是外部能量耗散，因为可以通过改变锚点的几何结构来改善其性能。本文应用完美匹配层（Perfectly Matched Layers，PML）方法，针对锚点结构引起的能量耗散进行一定的分析，讨论锚点结构的变化对圆盘体模态谐振器固有频率和锚点耗散品质因子的影响。

1　完美匹配层方法

完美匹配层方法最早是由Berenger［3］在研究电磁波传播问题时提出的，其思路是设置一定厚度的吸收边界域，不同于前人的地方是，没有设置边界域的材料属性，而是从坐标的复值变换来考虑。后来又经过一些学者的演化与推进，逐渐发展为一种通用的方法，使得任意入射角、频率的波都可以无反射地入射到吸收域，并且可以应用于任何线性波动方程［4-6］。

一个无限大区域的PML模型可以分解为两个子域：一个子域准确描述所求问题的实际方程，另一个子域用来描述远场辐射边界条件效应。所谓“完美匹配”，是指该吸收层具有两种特性：一是边界“透明”，即波可以任意穿过而不引起反射；二是层内“吸收”，即波在其内传播是指数衰减的。为了更好地解释PML的工作原理，下面以波的一维传播问题为例进行详细说明。

1.1一维弹性波理论

对于一个坐标为（0，∞）的半无限长的杆，纵波以速度c在其中传播，描述该运动的一维波动方程［7］如下

其中u（x，t）代表位移。采用分离变量的方法，将方程的解设为u（x，t）=U（x）eiωt，带入方程（1）得到赫姆霍兹方程（Helmholtz equation）

其中k=ω/c，称作波数。

方程（2）的解的形式为

其中cout代表出射波从原点传播到无穷远处时的波幅，cin代表入射波从无穷远处传播到原点时的波幅。一般认为在无穷远处是没有波源的，所以从物理角度来看，此处应有cin=0。

1.2一维弹性波在完美匹配层中传播

进行如下坐标变换，将坐标从实数域映射到复数域

其中λ：R→C是一个非零的连续函数，两端求导可以推导得到x^和x的关系如下

假设变换后的坐标x^是赫姆霍兹方程（2）的独立变量，则由上边的变换可以得到如下方程

方程（6）描述了波在完美匹配介质中的传播特性。

假设

则方程（6）的解的形式变为

此处，只要令σ=0，则方程（6）的解与原赫姆霍兹方程（2）的解是一致的。而当σ＞0时，波会在其传播方向上衰减，出射波的振幅随x的增大而衰减，入射波的振幅随x的减小而衰减。这里可以令σ在区间［0，L］内为零，在［L，∞）内为σ=β（ξ-L），如图1所示。那么对于x＞L，出射波的振幅为coute-β（x-L）2/2，入射波的振幅为cineβ（x-L）2/2。

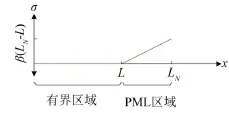
图1　一维弹性波分段线性衰减函数

当波通过完美匹配介质时，其幅值迅速衰减，利用这个特点，可以用有限区域来近似模拟无限区域问题，即对L＞LN的区域，令U（LN）=0。这就是完美匹配层的思想，完美匹配层就是有限区域的完美匹配介质。

假设令U（0）=1，U（LN）=0，写成以出射波和入射波振幅来表示的矩阵形式为

其中α=β（LN-L）2，可以求得

即使α很小时，有限区域的解也能很好的近似无限区域的解。对于α≈4.6时，只有1%的出射波会反射。对于连续问题，增大α可以减小波的反射。而对于由有限差分或有限元近似得到的离散方程，增大α需要格外注意。如果β较大，进入PML的波会迅速衰减掉，有效地创建一个边界层，但是如果离散的太粗糙，数值解会被恶意的反射污染。

2　方法验证

图2为最常用的中心支撑圆盘体模态谐振器示意图，在谐振圆盘上有两个区域：一是支撑区域，该区域位于支撑梁的上方，材料为多晶硅；二是外部区域，该区域位于支撑区域外部，材料为多晶金刚石［8］。支撑梁的中轴线与谐振圆盘对齐，材料为多晶硅。

应用上述完美匹配层方法，结合有限元数值仿真计算，将中心支撑圆盘体模态谐振器建模为如图3所示的有限元模型。其中基底被分为有界区域和完美匹配层两个部分，有界区域如同上一节所述，对波没有吸收作用，并且在其边界处，波可以任意穿过而不引起反射；外侧部分为完美匹配层，对波有指数衰减的作用。这里之所以将基底模型建为球形是为了使波垂直入射，尽可能少的减小反射。这样便以一个有限区域模拟了无限大基底中波的传播问题。

图2　中心支撑圆盘体模态谐振器

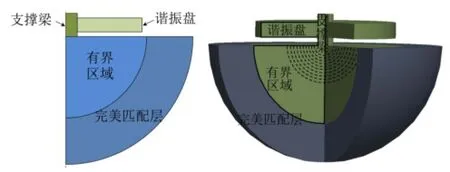
图3　有限元模型示意图

本文得到的固有频率和锚点耗散品质因子同文献［9］计算得到的结果对比列入表1中。可以看出，本文得到的结果同文献中计算出的结果相差不大，说明本文方法是准确的。

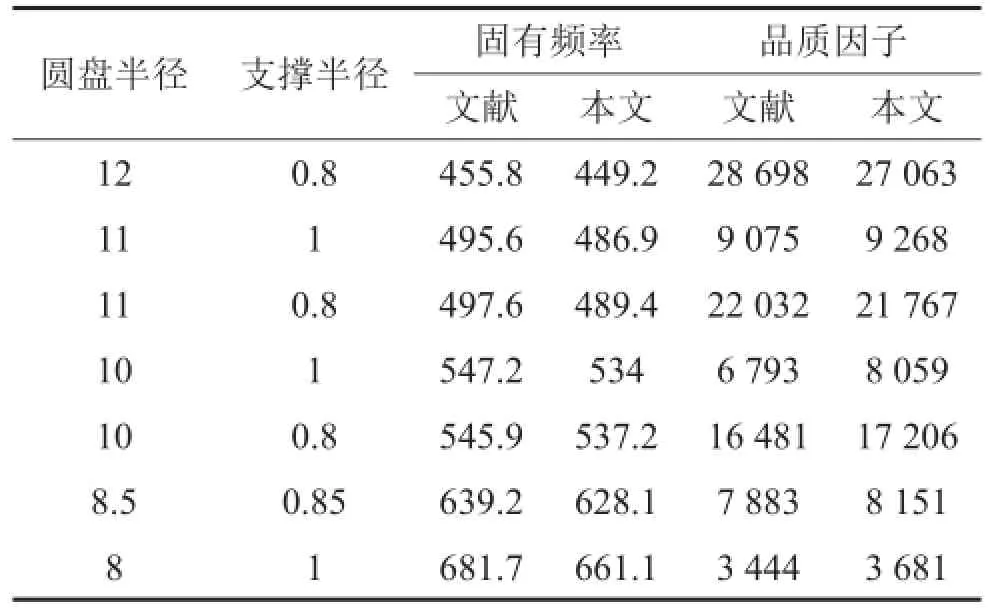
表1　计算结果同文献结果对比

3　结果讨论与分析

圆盘体模态谐振器能量的耗散机理是：谐振盘的径向振动带动支撑梁的径向振动，而支撑梁的径向振动引起其轴向的变形，进而诱导出支撑梁与基底接触区域的正应力，产生弹性波，该波通过基底向无穷远处传播并逐渐耗散掉，产生能量耗散。因此，从机理出发，改变支撑梁的结构应该会对能量耗散产生一定的改善。基于此种考虑，设计两种支撑梁结构来探索其几何结构对锚点能量耗散的影响。

3.1圆锥台支撑梁

图4为圆锥台支撑梁圆盘体模态谐振器1/4截面示意图。

图4　圆锥台支撑梁1/4截面示意图

改变圆锥台支撑梁底角θ的值，可以改变支撑梁与基底接触区域的面积，当θ为锐角时，支撑梁与基底接触区域的面积较原来增大，当θ为钝角时，支撑梁与基底接触区域的面积较原来减小。以θ为自变量，讨论θ的变化对圆盘谐振器固有频率和锚点耗散品质因子的影响，所得结果如图5所示。

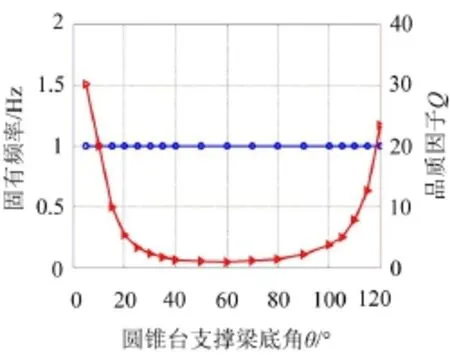
图5　圆盘谐振器固有频率和品质因子随圆锥台支撑梁底角变化关系

由图5可以看出，改变圆锥台支撑梁底角θ对圆盘谐振器的固有频率几乎没有任何影响，这是因为圆盘谐振器振动时主要是面内振动，其刚度主要由圆盘本身及与其接触区域的支撑梁来决定，这部分区域在圆锥台支撑梁这种结构中没有变化，因此圆盘谐振器固有频率没有变化。但是，改变支撑梁与基底接触区域面积的大小会对这部分的正应力产生影响，而正应力又是产生弹性波（锚点耗散来源）的原因，因此随着θ的变化，品质因子有较明显的变化。当θ＜40°时，θ越小，谐振器的品质因子越高，因为随着θ的减小，支撑梁与基底的接触区域逐渐增大，正应力逐渐减小，所产生的弹性波能量减少，所以品质因子增大；而当θ＞90°（90°时支撑梁为圆柱支撑梁）时，随着θ的增大，支撑梁与基底接触区域面积减小，正应力增大，弹性波能量也应该会有增加，但是接触区域的减小使能够产生弹性波的区域随之减小，而这又是此种情况下的主导因素，因此锚点处耗散的能量减小，品质因子增大；当40°≤θ≤90°时，由于支撑梁与基底接触区域面积变化不大，所以品质因子也变化不大。

3.2空心支撑梁

这种结构设计的出发点是减小支撑梁与基底接触区域面积，以减小接触区的正应力，从而减小弹性波的产生来提高谐振器的品质因子。其1/4截面示意图如图6所示。

图6　空心支撑梁1/4截面示意图

改变空心支撑梁内径大小，计算得到的结果如图7所示。

图7　圆盘谐振器固有频率和品质因子随空心支撑梁内径变化关系

固有频率随着空心支撑梁内径的增加几乎没有变化，说明无论是空心梁还是实心梁，其径向刚度几乎不随内径变化而变化。而品质因子却随着空心支撑梁内径的增大而增大，并且从图7中也可以发现，当内径Rh＜0.5时，品质因子的增长速率比较慢，而当Rh＞0.5后，品质因子随着内径的增大而迅速增大，因为此时支撑梁壁板已经变得很薄，同基底的接触区域很小，能量通过其的耗散量也变得非常少，品质因子因此就迅速增加，但是薄壁板的支撑梁强度较差，容易损坏，因此设计中不能做的太薄，根据实际情况选择合适的内径即可。

4　结语

应用完美匹配层方法，用有限区域来描述无限区域内的入射波吸收问题，针对中心支撑圆盘体模态谐振器的能量耗散特性进行了分析，设计出两种新型的锚点支撑结构，并讨论其几何结构的变化对谐振器性能的影响。结果表明：圆锥台支撑梁底角θ在小于20°和大于100°时可以明显提高谐振器的锚点耗散品质因子；空心支撑梁在支撑梁内径Rh大于0.5 μm时，其锚点耗散品质因子得到显著提升，但优化工作中应注意，增大内径虽然有助于提高能量的利用率，但是内径太大会使支撑梁的壁板较薄，强度会减弱，因此，在设计时应选取满足要求的最小内径值。

［1］Park Y H，Park K.High-fidelity modeling of MEMS resonators.Part I.Anchor loss mechanisms through substrate［J］.JournalofMicroelectro-mechanical Systems，2004，13（2）:238-247.

［2］孙玉国.RF MEMS开关吸合时间Runge-Kutta求解［J］.噪声与振动控制，2009，29（2）：97-98.

［3］Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of Computational Physics，1994，114（2）:185-200.

［4］Collino F，Monk P.The perfectly matched layer in curvilinear coordinates［J］.SIAM Journal on Scientific Computing，1998，19（6）:2061-2090.

［5］Teixeira F，Chew W.Complex space approach to perfectly matched layers:a review and some new developments［J］. InternationalJournalofNumericalModelling: Electronic Networks，Devices and Fields，2000，13（5）: 441-455.

［6］TurkelE，YefetA.AbsorbingPMLboundarylayersforwavelike equations［J］.Applied Numerical Mathematics，1998，27（4）:533-557.

［7］吴国荣.变截面导管声传输特性研究［J］.噪声与振动控制，2007，27（1）：104-105.

［8］Gruen D M，Liu S，Krauss A R，et al.Fullerenes as precursors for diamond film growth without hydrogen or oxygen additions［J］.Applied Physics Letters，1994，64 （12）:1502-1504.

［9］Hao Z，Ayazi F.Support loss in the radial bulk-mode vibrations of center-supported micromechanical disk resonators［J］.Sensors and Actuators A:Physical，2007，134（2）:582-593.

Energy DissipationAnalysis of Micromechanical Resonators with VariableAnchor Structures

ZHANGSha1，ZHANG Wen-ming2
（State Key Laboratory of Mechanical System and Vibration，Shanghai Jiaotong University，Shanghai 200240，China）

Energy dissipation of micromechanical resonators is always inevitable in vibration process.There are several energy dissipation mechanisms，such as air damping dissipation，thermo-elastic damping dissipation，anchor loss，surface dissipation and so on.Of them，anchor loss is the main energy dissipation mechanism.In this paper，the perfectly matched layers method was adopted to transform the incident wave absorption problem in infinite domain into that in finite domain.Two different anchor structures of centrally-supported bulk-mode disk resonator were designed.And the influence of the geometrical changes of the structure on the inherent frequencies and anchor loss quality factor of the bulk mode disk resonator was discussed.The results show that the anchor loss quality factor can be greatly improved and the energy utilization efficiency can be raised by changing the anchor structure of the resonator.

vibration and wave；micromechanical resonator；anchor loss；perfectly matched layers；structure optimization

TB535.1

ADOI编码：10.3969/j.issn.1006-1335.2015.05.007

1006-1355（2015）05-0039-04

2015－01－21

国家自然科学基金项目（11322215）；霍英东青年教师基金项目（141050）

张厦（1987－），男，河北石家庄人，硕士生，主要研究方向：微机电系统动力学。

E-mail:ziying1282@sjtu.edu.cn

张文明（1978－），男，博士生导师。

E-mail:wenmingz@sjtu.edu.cn