改进的基于模糊推理的车辆跟驰行为分析方法*

邱小平 孙若晓 于丹 杨达，2†

(1．西南交通大学交通运输与物流学院，四川成都610031;2．西南交通大学综合交通运输智能化国家地方联合工程实验室，四川成都610031;3．综合运输四川省重点实验室，四川成都610031)

作为微观交通流理论最基本的组成部分之一，车辆跟驰模型研究的是同一车道行驶车辆的跟驰行为．此类模型的探讨对城市交通拥堵减缓、交通安全保障、智能驾驶等领域的研究都有着十分重要的作用．从20世纪50年代开始，各国学者已经开始车辆跟驰行为的研究，发展出来的模型包括GHR模型、线性模型、安全距离模型、心理模型和基于模型推理的模型［1-2］．驾驶员是跟驰单元中的操控者和决策者，根据自己的驾驶经验应对前车的运行状况，但并不是所有的驾驶经验在跟驰行驶中都是可行的，因此研究基于驾驶员心理、生理特征的车辆跟驰模糊推理模型就变得十分有必要［3-5］．模糊推理的方法可以有效描述那些无法用精确数学模型表示的模糊概念，最大程度上还原车辆跟驰过程中驾驶员应对复杂环境的机理，如前车速度较“快”，相对速度较“小”，车间距“太远”，应采取较“大”加速度等．

Kikuchi等［6］最早将模糊推理应用于跟驰行为的研究，在他们的模糊处理过程中，模糊输入变量为相对距离Δx、相对速度Δv、前车加速度an依次被划分为6、6、12个模糊集，规则库输出变量后车加速度an等于前车的加速度加上与Δx、Δv有关的调整量．McDonald等［7］提出建立了一种基于模糊推理理论的微观交通流模型，并选取Δv、相对距离DS与期望间距SD的比值DSSD作为输入变量，推理结果表明SD在跟驰行为中作用显著，这也是与现实状况相一致的．之后利用模糊推理方法探究车辆跟驰行为在学术界引起一段热潮，各国学者针对模糊推理过程中各个推理环节展开研究，并进一步验证了模糊推理理论的实用性和适用性，为更深层次的车辆跟驰理论研究奠定了基础［8-11］．

输入变量模糊集个数、各模糊集对应的隶属度函数、模糊推理规则库和去模糊化方法等是模糊推理的关键部分，也直接影响并制约着该方法在跟驰领域的应用．传统获取车辆跟驰隶属度函数和模糊推理规则库的方法主要是专家经验法与主观指定法．McDonald等［7］在确定车辆跟驰的模糊推理规则库时，以驾驶员对环境的主观认定作为数据源，之后利用统计学的方法得到推理规则．文献［8，12］中也用类似的方法来确定车辆跟驰隶属度函数．Xiong等［13］使用最小二乘法拟合获取变量的隶属度函数，拟合过程中同样使用专家经验获取变量隶属度．除此之外，各国学者也尝试使用直接指定法［9，14-15］来获取车辆跟驰模糊推理的隶属度函数和模糊推理规则库．传统的隶属函数和规则库的确定方法均过多依赖专家经验，这无疑给推理结果造成极大的误差．

文中通过研究模糊聚类分析方法的科学性与适用性，并考虑到高斯隶属度函数良好的抗干扰能力，提出一种基于聚类分析的确定车辆跟驰模糊推理隶属函数的方法，利用数据推理出车辆跟驰模糊推理系统的规则库，该方法能根据各输入、输出变量数据内部关联性，确定最佳阈值以将对应变量划分为最佳模糊集，再根据公式求出各个模糊集对应的隶属度函数;经过对比分析Takagi-Sugeno模糊推理方法的优越性，首次提出使用Takagi-Sugeno方法对车辆跟驰模糊推理系统进行模糊推理和去模糊化处理．并根据Takagi-Sugeno推理方法的特征，设计一种基于最大隶属原则确定车辆跟驰模糊推理规则库的方法．使用NGSIM车辆跟驰数据验证上述模糊推理系统建立过程所用方法的有效性，并将模糊推理结果与Gipps车辆跟驰模型的结果进行对比，列出两种研究车辆跟驰方法的误差．

1 车辆跟驰模糊推理系统的建立

1．1 模糊推理系统

模糊推理系统是以模糊集合论为基础的描述工具，将现实生活中事物发展形态划分为不同的模糊集合，从而模拟人脑处理模糊事务的过程，是用来表示人思维中近似推理的复杂系统．车辆跟驰行为中的驾驶员对前车驾驶员动作所做的反应不是确定性的一一对应关系，其驾驶行为存在“非精确性”、“非对称性”、“间断性”等特征［9］．驾驶员在跟驰单元中获取模型的信息，再根据自己的驾驶经验采取加速或减速措施，这样一些模糊理论的推理适合用模糊逻辑进行分析，因此一经提出就受到国内外学者的广泛关注［8-10，12-15］．车辆跟驰的模糊推理系统由变量输入、模糊化处理、模糊推理规则库、推理方法选取和去模糊化输出5部分组成，其基本构成图如图1所示．

图1 模糊推理系统的构成Fig．1 Consistencies of a fuzzy inference system

设车辆跟驰模糊推理系统的一个输入输出组合为{(xi，yi)|i=1，2，…，m}，xi=(xi1，xi2，…，xin)，其中m为数据组合的总数，n为每一个输入组合包含的变量个数．模糊推理的输入输出部分都需要将精确值进行模糊化处理，以［0，1］的值表示精确值隶属于模糊集的程度．高斯隶属函数是模糊推理系统中一种常用的隶属函数形式，它具有良好的抗干扰能力，能够更精确反应人的认知特性．设μ为输入的精确值，A为模糊化之后的模糊集合，则其对应的高斯隶属函数的表达式为

式中，σ表示模糊集A内包含数据的标准差，它决定了高斯隶属函数的坡度．

1．2 模糊聚类确定车辆跟驰隶属函数

在构建车辆跟驰模糊推理系统时，输入、输出变量的模糊集划分和隶属函数确定是首先要解决的问题．由于传统确定方法大多使用专家经验法或人工指定，使得推理结果或多或少受到人为的干扰．文中尝试使用模糊聚类的方法，根据车辆跟驰各个变量数据内部的关联性与相似性进行划分，并由高斯隶属函数参数的统计学意义计算出各个变量模糊集对应的隶属度函数．首先定义基于模糊聚类的车辆跟驰模糊推理系统的输入、输出变量形式:

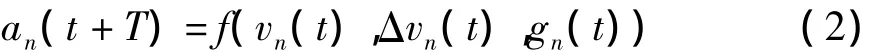
式中:an(t+T)为后车t+T时刻加速度，T为反应时间;f(·)表示输出变量an(t+T)与所有输入变量的某种关系;vn(t)为t时刻后车速度;Δvn(t)为t时刻前后两车相对速度，Δvn(t)=vn-1(t)-vn(t);gn(t)为t时刻两车间距．

该模糊推理系统第k行输入与输出组合为:{(xk，［an(t+T)］k)|k=1，2，…，M}，其中 xk=(vn，Δvn，gn)k．现以 vn(t)为例，对其进行模糊聚类，由上面的定义可知vn(t)为车辆跟驰模糊推理第1个输入变量，且 vn(t)包含的数据为(x1，1，x2，1，…，xM，1)T．首先求出vn(t)包含数据中任意两个元素xi，1与 xj，1之间的相似系数 ri，j=R(xi，1，xj，1)，从而建立相应的模糊相似矩阵R．确定ri，j的方法主要有距离法、相似系数法等传统聚类分析法，文中选用欧几里得距离法［16］．之后，使用传递闭包法求出上述模糊相似矩阵R对应的模糊等价矩阵Re，传递闭包法的计算公式如下:

式中，xti，1为第ti行第1列的值．通常，当对输入输出变量划分模糊集并求隶属函数时，会通过等间距网格划分模糊区域，使相邻两个模糊集交叉口的隶属度近似取为0．5．当使用上述方法划分模糊区域时，由于划分后的网格属于非均匀的，则会因各个模糊集函数的绝对不规则性，及交叉范围过小，产生较多的相互矛盾规则，从而影响模糊推理规则库的生成和模型的精度［17］．鉴于上述原因，当获取各个模糊集的中心点之后，按照以下的规则求其跨度．比较某模糊集中心μt与相邻模糊集合中心μa、μc的间距，则高斯隶属函数跨度为

对前车速度vn划分的第1个模糊集A1，通常认为当前车速度绝对小时，其绝对隶属于此模糊集，即此时隶属度等于1，对模糊集AK也可做相似分析．因此，在对聚类出的各个模糊集的隶属函数调整之后，需要再次对A1、AK的隶属函数重新调整:

1．3 车辆跟驰模糊推理规则库建立

模糊推理规则库是由模糊推理系统中的全部模糊规则构成的，也是模糊推理系统的核心部分之一，从某种意义上来说，模糊推理系统的其他部分都是为了有效执行规则库中的这些规则而存在的．设vn(t)、Δvn(t)、gn(t)、an(t+T)依次可划分为 AiKi个模糊集(i=1，2，3，4)，则一条简单的推理规则可表示如下［18-19］:

其中:A1t1为vn(t)的第t1个模糊集，其他变量类似定义ti=1，2，…，Ki;H(t1t2t3)为该条推理规则下的实数值．给定各变量的模糊集个数之后，此车辆跟驰模糊推理规则库中共包含推理规则的个数为K1×K2×K3．

求H(t1t2t3)时，可参照文献［20］中的启发式方法，定义第k个输入输出序列{(xk，［an(t+T)］k)}的权重系数为

式中，xk=(vn，Δvn，gn)k，μt1t2t3(xk)= μt1(vn)·μt2(Δvn)·μt3(gn)，μt1(vn)为vn对应第t1个模糊集的隶属度．α表示各个输入变量对应模糊推理规则R(t1t2t3)权重，H(t1t2t3)则可由下式求出:

之后，利用最大隶属原则，根据R(t1t2t3)推理的后车加速度值确定H(t1t2t3)所属的模糊集．R(t1t2t3)将改写为纯语言描述的推理规则 R*(t1t2t3)，方法为［20］

1．4 Takagi-Sugeno去模糊化处理

去模糊化是指确定一个最具代表性的值来替代模糊集合，由于输入、输出阶段进行模糊化处理的方法不同，去模糊化所获得的精确值也会有所差异．确定模糊推理与去模糊化的方法时，一般要参照以下原则:

(1)简便性，即所选用的模糊推理与去模糊化方法足够简单，同时应保证模糊推理系统的有效性与实用性;

(2)鲁棒性，即使用的模糊推理与去模糊化方法能保证模糊集合的微小变化不会引起去模糊化精确值的大幅变化．

由于传统Mamdani、Larsen等模糊推理法得到的是输出变量对应的隶属度函数值或离散模糊集合，需要对每一个输出变量的模糊集合进行去模糊化处理，并将多条推理规则的结果合成，才能得到最终的输出变量精确值．而Takagi-Sugeno方法则将去模糊化结合到模糊推理系统中，其输出为精确值，由于减少了单独为各条模糊推理规则进行去模糊化处理的工作量，必然使得车辆跟驰模糊推理系统的计算过程得到有效简化．基于此文中首次使用Takagi-Sugeno模糊推理和去模糊化的方法求解出车辆跟驰模糊推理系统的后车加速度［19，21-23］．对于给定的车辆跟驰输入数据 xk=(vn，Δvn，gn)k，其推理结果［an(t+T)］k可由下式求出:

2 车辆跟驰数据描述

上述提出的确定车辆跟驰模糊推理系统的方法旨在摒弃传统专家经验法，根据数据本身的特点来建立对应的隶属度函数以及对立规则，为验证文中提出方法的有效性，下面将使用真实的车辆跟驰NGSIM数据进行检验．该数据来自于2005年6月15日由美国联邦公路局的Next Generation Simulation(NGSIM)研究计划，通过在加州US-101公路指定地点的跟驰车辆动态行驶轨迹特征数据而获得的．数据获取的时段为7:50～8:35，通过在高空架设8台高清相机来捕捉车辆行驶轨迹和微观交通量数据．这套数据可以综合反映多个车道中车辆的速度、位置、车身长度以及加速度等信息，时间精确到1．1s，是研究跟驰模型时参数标定、行为分析等方面所通用的理想数据．该项目虽然是由美国高速公路管理局主持并采集的，但车辆跟驰特性具有明显的一般性，几乎不受国籍和区域的影响，并且NGSIM数据是在一般环境下采集到的，因此这套数据备受学者关注，文献［24-26］均是使用这套数据对车辆跟驰理论进行研究．

文中研究的是在一般环境中的车辆跟驰行为，在模糊推理系统各环节确定与结果分析中也将采用上述数据源．然而，文章旨在研究单车道中的车辆跟驰特征，而NGSIM则主要反应多车道车辆行驶状况，因此在获取数据源之后，还需对数据做如下甄选:

(1)选取有代表性的一般环境(气候、道路、行驶轨迹、驾驶员等信息)中的跟驰行驶数据为文中所需数据;

(2)数据选取时，将前后跟驰的两辆车划分为一个单元;

(3)每一个被选择的跟驰单元的两辆车具有如下特征，即在同一车道中跟随行驶(跟随车既不变换车行道，又不超速行驶);

(4)当一个被选取单元中的前后两辆车跟驰间距过大时，认为该数据不具有明显的跟驰特征，而将此跟驰单元的两辆车行驶轨迹数据筛除;

(5)选取的车辆跟驰行驶时间为27s．

经过对数据进行上述几个步骤的筛选和处理，可以得到文中模糊推理系统各环节建立和模糊推理结果评价所需要的6万多条样本数据，所获得的这些数据样本具有一般的代表性，且其数目较为庞大，可以较精确保证所建立的车辆跟驰模糊推理系统的真实、有效，也可以为模糊推理的结果验证提供足够多的样本数据源．

3 确定最佳阈值与隶属度函数

3．1 模糊聚类最佳阈值确定

式中，K1为分类总数，Nt、μt分别为第 t个分类样本数、聚类中心，¯x为数据样本vn的平均值．由统计学意义可知，此F统计量服从(K1-1，M-K1)的F分布．F统计量能够反映每个变量划分的模糊聚类内部与各变量之间的紧密程度，其值越大，说明各变量之间的联系越分散而对应此变量的各类间联系越紧密，则模糊聚类效果越好．

将上述车辆跟驰模糊推理系统建立过程进行Matlab编码实现，并选取输入变量为t时刻后车速度vn(t)、相对速度Δvn(t)、两车间距gn(t)．输出变量为后车加速度an(t+T)，反应时间T取1．1 s．指定各个变量的-阈值以对其划分成不同的模糊聚类，并将各个变量对应其分类数下的F统计量汇总成表1．在为变量划分模糊集时，原则上不应划分出过多的模糊集，基于此文中选取模糊集划分个数的范围为2～6．由表1的汇总结果可以看出，输入和输出变量 vn(t)、Δvn(t)、gn(t)、an(t+T)对应的最佳模糊聚类个数分别为 3、3、4、3．

表1 车辆跟驰输入输出变量在不同聚类下的F统计量Table 1 F values of different clustering for input-output variables

3．2 车辆跟驰隶属度函数分析

由第3．1节的讨论结果可知，vn(t)被划分为PS(正小)、PM(正中)、PB(正大)3 个模糊集，Δvn(t)被划分为NM(负中)、ZE(零)、PM(正中)3个模糊集，gn(t)被划分为 PS、PM(正中小)、PMB(正中大)、PB 4个模糊集，an(t+T)被划分为NM、ZE、PM 3个模糊集．图2各个图像从左至右将显示各个变量模糊集对应的隶属度函数．

由现实跟驰情形并结合图2(a)可知，后车速度vn(t)的取值均大于0，图中其隶属度函数横坐标轴正是从1．5 m/s开始的，并且当速度大于15 m/s时可认为处于该范围内的速度应绝对隶属于模糊集PB，这正与驾驶员感受的速度信息相符合，也更接近事实．通过分析可看出，利用真实数据结合模糊聚类方法求出的隶属度函数只受该模糊集中数据的影响，而受到人为因素的干扰较少，可以保证各个变量所划分的模糊集和求出的对应隶属度函数更加真实有效．另一方面，由于传统隶属度函数确定方法(专家法)只依赖专家经验和图形美观化，将使划分的模糊集和对应的隶属度函数趋向于对称化．图2可以充分证明，模糊化处理环节所使用的隶属函数确定方法直接影响并决定了各变量的模糊集划分和隶属度函数的确定．并且各模糊集对应的隶属度函数大多数情况下展现了一种不规则、不对称性，产生这种现象的原因不难理解，驾驶员对外界环境感受有所差异，而且其对刺激做出的反应也会存在很大的不对称性［28-29］．

图2 车辆跟驰模糊推理系统隶属度函数Fig．2 Membership functions of car-following fuzzy inference system

4 模型评价

4．1 Gipps车辆跟驰模型

Gipps提出来的基于安全行驶距离的车辆跟驰模型综合考虑车辆的加速度约束和安全跟驰距离的约束，可以较好地仿真模拟真实交通中的车辆跟驰行为，被国内外学者当作评价其他车辆跟驰模型的“参考系”．Gipps车辆跟驰理论认为，在车辆跟驰过程中，当前车遇到紧急状况而突然减速时，跟驰车驾驶员将选用一个安全速度使两车不致发生碰撞．安全速度的假设能够有效地表现驾驶员的心理-生理特性，而且其实用性和有效性也得到充分证明．然而，Gipps并没有用真实的车辆跟驰数据对其模型中有关的参数进行标定，而是通过使用假定的参数值模拟多车跟驰的情景，文中将试图用实测的NGSIM数据对Gipps车辆跟驰模型进行参数标定，并通过与经典Gipps车辆跟驰模型进行对比来评价文中建立的车辆跟驰模糊推理系统的有效性，下面给出Gipps车辆跟驰模型的基本表达式［30］:

式中，αn、Vn、bn、bn-1为待标定的参数，αn表示第 n车能获得的最大加速度，Vn表示第n车在此交通条件下的期望速度，bn-1、bn分别表示前车n-1和跟驰车n的最大减速度．使用文献［26，31-32］提出的考虑稳定状态时的车辆跟驰模型的标定方法，并利用Matlab软件遗传算法软件包中的GA函数，然后将NGSIM数据源的代入Gipps模型，求出模型中涉及到的参数标定值结果为:αn=1．2，Vn=24．17，bn=-1．0，bn-1=-1．0．

4．2 评价指标选取

车辆跟驰模糊推理系统隶属函数、推理规则等各环节确定以后，选用适当的统计学变量对模型推理结果展开评价，所用的统计量［15，26，31］主要有:平均误差(eME)、平均绝对误差(eMAE)、均方根值误差(eRMSE)、平均绝对相对误差(eMARE)，各统计量计算公式如下:

式中，M表示用以评价的数据样本个数，Zr，k表示第k辆车速度、加速度或位置对应的实测数据，Zs，k表示第k辆车速度、加速度或位置对应的仿真数据．

4．3 评价结果与分析

根据得到的车辆跟驰高斯隶属函数、模糊推理规则库等数据，可建立相应的车辆跟驰模糊推理系统．按照前文所述，选取的输入变量为:t时刻后车速度vn(t)、相对速度Δvn(t)、两车间距gn(t)，输出变量为经反应时间T后的跟随车加速度an(t+T)．车辆跟驰模糊推理系统(FIS)的确定还应标定式(8)中的参数α，根据评价误差计算式(12)-(15)，针对不同α取值下的eMARE，求出对应的模型误差并将结果绘制成图3．

图3 不同α取值下的eMARE变化Fig．3 eMAREvalues under different α

从图3可以看出，随着α取值的变大，eMARE总体呈现上升的趋势，并存在全局最小值，对应的α为3．3．将模糊推理系统α取为固定值3．3，推理出后车加速度，并利用仿真出来的后车加速度求出实时动态变化的后车速度值．分别将车辆跟驰模糊推理系统与Gipps模型的仿真结果带入评价误差计算式(12)-(15)，求出两个模型彼此对应的误差，得到如表2所示的评价结果．

表2 车辆跟驰模糊推理结果与Gipps模型对比评价Table 2 Evaluation results of FIS and Gipps model

从评价结果(表2)中可以看出，利用文中提出的方法建立车辆跟驰模糊推理系统，各类误差指数推理结果相对较小，并且与传统的Gipps模型相比具有明显的优越性．首先，FIS的大多数误差指标均小于Gipps模型中相应的指标;虽然FIS模型对应的eME不如Gipps模型理想，但平均误差只表示全部模型推理结果与实测值之间偏差大小的算术平均值，并不能绝对反应模型真实的拟合效果;而且，就eMARE来说，FIS模型和Gipps模型相比较时，FIS关于加速度、速度误差指标的仿真精度提高值分别为0．037m/s2、0．017 m/s．也就意味着 FIS 仿真结果与NGSIM数据更加接近，这也从微观层面方面证明了FIS模型在研究车辆跟驰模型等有关交通流理论中的有效性与实用性．为了更直观对比FIS模型与Gipps模型的仿真效果，任意选择两辆车的真实跟驰数据与两模型仿真数据绘制如图4(a)、4(b)所示．由图可知，FIS模型更加贴合真实数据，也更能展现数据波动性，因此可为今后跟驰领域的研究提供参考．

图4 模糊推理结果与Gipps模型对比Fig．4 Comparison of FIS and Gipps models

5 结论

由于驾驶员心理生理特性和在跟驰过程中感知有关信息的不确定性，使得模糊推理方法一度成为解决此类非精确性问题的有效方法．传统车辆跟驰模糊推理系统的隶属度函数确定、规则库建立很大程度上取决于专家决策，而极少考虑实测数据的特征和内部关联性，从而造成模糊推理结果产生较大误差，并在一定程度上延缓模糊推理理论在车辆跟驰领域的应用．针对上述问题，文中提出建立车辆跟驰模糊推理系统各环节的有效方法．文中提出使用模糊聚类的方法为推理系统的输入、输出各变量划分模糊集并求出对应隶属度函数，采用启发式的方法求出车辆跟驰模糊推理系统对的模糊推理规则库，通过比较模糊推理过程中去模糊化方法的适用性和有效性，首次使用Takagi-Sugeno方法对车辆跟驰模糊推理系统进行去模糊化处理，之后对模型中有关参数进行标定，并与Gipps模型进行对比评价，以验证文中提出方法下得到的模糊推理系统的科学性与有效性，对文章总结可得如下结论:

(1)采用NGSIM数据求得的输入输出变量vn(t)、Δvn(t)、gn(t)、an(t+T)对应的最佳模糊集个数分别为 3、3、4、3;

(2)由模糊聚类求出的车辆跟驰模糊推理系统的隶属度函数存在不对称性，这是由于数据本身特征和驾驶员心理生理特性造成的，与事实相符合;

(3)车辆跟驰模糊推理系统和传统Gipps模型相比，具有更高的精度，能够比较真实地反应驾驶员在跟驰过程中的心理生理特性，可以为分析驾驶员的跟驰行为提供参考．

在建立车辆跟驰的模糊推理系统过程中，隶属度函数确定和规则库建立影响并制约着模糊推理结果，在进一步的研究中可对隶属函数、规则库确定的不同方法进行讨论;并将考虑驾驶员对前车速度变化刺激所做出反应的不对称性．

［1］曹宝贵，杨兆生．一种改进的车辆跟驰动力学模型［J］．华南理工大学学报:自然科学版，2011，39(10):96-99．Cao Bao-gui，Yang Zhao-sheng．An improved car-following dynamic model［J］．Journal of South China University of Technology:Natural Science Edition，2011，39(10):96-99．

［2］Brackstone M，Mcdonald M．Car-following:a historical review ［J］．Transportation Research Part F:Traffic Psychology and Behaviour，1999，2(4):181-196．

［3］Michaels R M．Perceptual factors in car following［C］∥Proceedings of the 2nd International Symposium on the Theory of Road Traffic Flow．Paris:OECD，1963:44-59．

［4］Wiedemann R．Simulation of road traffic in traffic flow［R］．Karlsruhe:Universityof Karlsruhe(TH)，1974．

［5］Andersen G J，Saucer C W．Optical information for car following:The driving by visual angle(DVA)model［J］．Human Factors:the Journal of the Human Factors and Ergonomics Society，2007，49(5):878-896．

［6］Kikuchi S，Chakroborty P．Car-following model based on fuzzy inference system［J］．Transportation Research Record，1992，1(1365):82-91．

［7］McDonald M，Wu J，Brackstone M．Development of a fuzzy logic based microscopic motorway simulation model［C］∥Proceedings of Intelligent Transportation Systems Council．Boston:Institute of Electrical and Electronics Engineers，1997:82-87．

［8］贾洪飞，隽志才，王晓原．基于模糊推断的车辆跟驰模型［J］．中国公路学报，2001，14(2):81-83．Jia Hong-fei，Juan Zhi-cai，Wang Xiao-yuan．Car-following model based on fuzzy inference system ［J］．China Journal of Highway and Transport，2001，14(2):81-83．

［9］王文清，王武宏，钟永刚，等．基于模糊推理的跟驰安全距离控制算法及实现［J］．交通运输工程学报，2003，3(1):72-75．Wang Wen-qing，Wang Wu-hong，Zhong Yong-gang，et al．Car-following safe distance control algorithm and implementation based on fuzzy inference［J］．Journal of Traffic and Transportation Engineering，2003，3(1):72-75．

［10］Mar Jeich，Lin Feng-jie，Lin Hung-ta，et al．The car following collision prevention controller based on the fuzzy basis function network ［J］．Fuzzy Sets and Systems，2003，139(1):167-183．

［11］Chakroborty Partha．Models of vehicular traffic:an engineering perspective［J］．Physica A:Statistical Mechanics and its Applications，2006，372(1):151-161．

［12］Wu Jianping，Brackstone Mark，McDonald Mike．Fuzzy sets and systems for a motorway microscopic simulation model［J］．Fuzzy Sets and Systems，2000，116(1):65-76．

［13］Xiong Qi-peng，Chen Zhi，Zeng Xiao-qing，et al．Development of membership degree functions of the car-following models based on fuzzy logic［J］．Second International Conference on Intelligent Computation Technology and Automation，2009，403(2):697-699．

［14］Mar Jeich，Lin Hung-ta．The car-following and lane-changing collision prevention system based on the cascaded fuzzy inference system［J］．IEEE Transactions on Vehicular Technology，2005，54(3):910-924．

［15］Khodayari Alireza，Kazemi Reza，Ghaffari Ali，et al．Design of an improved fuzzy logic based model for prediction of car following behavior［C］∥2011 IEEE International Conference on Mechatronics(ICM)．Istanbul:［s．n］，2011:200-205．

［16］孙逊，胡光锐，李剑萍．一种基于模糊聚类的隶属函数定义方法［J］．计算机应用与软件，2005，22(7):86-88．Sun Xun，Hu Guang-rui，Li Jian-ping．A method for definition of membership function based on fuzzy clustering［J］．Computer Application and Software，2005，22(7):86-88．

［17］袁兵，江丽，朱宏辉．一种模糊隶属函数的自动生成算法［J］．武汉理工大学学报:交通科学与工程版，2006，29(4):631-633．Yuan Bing，Jiang Li，Zhu Hong-hui．A novel algorithm for automatic generarion of fuzzy membership functions［J］．Journal of Wuhan University of Technology:Transportation Science ＆ Engineering，2006，29(4):631-633．

［18］Herrera Francisco，Lozano Manuel，Verdegay Jose Luis．A learning process for fuzzy control rules using genetic algorithms［J］．Fuzzy Sets and Systems，1998，100(1):143-158．

［19］Tsekouras George，Sarimveis Haralambos，Kavakli Evagelia，et al．A hierarchical fuzzy-clustering approach to fuzzy modeling［J］．Fuzzy Sets and Systems，2005，150(2):245-266．

［20］Nozaki Ken，Ishibuchi Hisao，Tanaka Hideo．A simple but powerful heuristic method for generating fuzzy rules from numerical data［J］．Fuzzy Sets and Systems，1997，86(3):251-270．

［21］Lee Chuen-Chien．Fuzzy logic in control systems:fuzzy logic controller．II［J］．IEEE Transactions on Systems，Man and Cybernetics，1990，20(2):419-435．

［22］Nomura Hiroyoshi，Hayashi Isao，Wakami Noboru．A learning method of fuzzy inference rules by descent method［C］∥IEEE International Conference on Fuzzy Systems．San Diego:CA，1992:203-210．

［23］钟飞，钟毓宁．Mamdani与 Sugeno型模糊推理的应用研究［J］．湖北工业大学学报，2005，20(2):28-30．Zhong Fei，Zhong Yu-ning．The application research of Mamdani and Sugeno style fuzzy inference ［J］．Journal of Hubei University of Technology，2005，20(2):28-30．

［24］Duret Aurélien，Buisson Christine，Chiabaut Nicolas．Estimating individual speed-spacing relationship and assessing ability of Newell＇s car-following model to reproduce trajectories［J］．Journal of the Transportation Research Board，2008，2088(1):188-197．

［25］Ossen Saskia，Hoogendoorn Serge P．Reliability of parameter values estimated using trajectory observations［J］．Journal of the Transportation Research Board，2009，2124(1):36-44．

［26］杨达，蒲云，杨飞，等．基于最优间距的车辆跟驰模型及其特性［J］．西南交通大学学报，2012，47(5):888-894．Yang Da，Pu Yun，Yang Fei，et al．Car-following model based on Optimal Distance and its characteristic analysis［J］．Journal of Southwest Jiaotong University，2012，47(5):888-894．

［27］孙才志，王敬东，潘俊．模糊聚类分析最佳聚类数的确定方法研究［J］．模糊系统与数学，2001，15(1):89-92．Sun Cai-zhi，Wang Jing-dong，Pan Jun．Research on method of determining the optimal class number of fuzzy cluster［J］．Fuzzy Systems and Mathematics，2001，15(1):89-92．

［28］Toledo Tomer．Integrated driving behavior modeling［D］．Cambridge:Northeastern University，2002．

［29］Li Li，Chen Xi-qun，Li Zhi-heng．Asymmetric stochastic Tau Theory in car-following ［J］．Transportation Research Part F:Traffic Psychology and Behaviour，2013，18(1):21-33．

［30］Gipps Peter G．A behavioural car-following model for computer simulation ［J］．Transportation Research Part B:Methodological，1981，15(2):105-111．

［31］Punzo Vincenzo，Simonelli Fulvio．Analysis and comparison of microscopic traffic flow models with real traffic microscopic data［J］．Journal of the Transportation Re-search Board，2005，1934(1):53-63．

［32］Brockfeld Elmar，Kühne Reinhart D，Wagner Peter．Calibration and validation of microscopic models of traffic flow ［J］．Journal of the Transportation Research Board，2005，1934(1):179-187．