基于3D数据和双尺度聚类算法的路面裂缝检测*
李伟 呼延菊 沙爱民 孙朝云 郝雪丽
(1.长安大学信息工程学院,陕西西安710064;2.长安大学 公路学院,陕西西安710064)
从传统的人工视觉路面裂缝识别到自动路面裂缝识别系统[1],路面裂缝[2-3]的各种检测技术发展迅速,为路面裂缝识别提供了越来越便利的检测技术.不同的裂缝检测技术在裂缝特征提取上各有其优缺点且分别取得了不同的路面裂缝识别效果,但其归根到底都是紧扣裂缝进行一系列的图像处理并使其效果不断优化,便于目标提取,即该类算法主要致力于裂缝特征[4]的提取,而很少考虑实际需要以及处理后的路面裂缝是否真正对应于同一条实际路面裂缝.首先,传统的裂缝特征提取算法使得预处理后的路面裂缝二值图相对于原始裂缝而言总是不同程度的缩小实际路面裂缝区域,更甚者经过多次处理后使得实际中同一条路面裂缝在图像上呈现断裂现象,断裂后的一条裂缝如果不进行及时的发现并修补,极有可能被当作两条甚至更多的裂缝处理,由于路面裂缝识别过程是一个串行的处理过程,其错误存在累积现象,这样使得后续处理中裂缝定位[5]等工作基于前端错误的结果进行,必然产生错误的裂缝识别结果,大大提高了裂缝识别的错误率,即存在“不补则错”的现象.再有,就实际而言,路面裂缝检测的目的在于准确分类裂缝、准确定位裂缝以及裂缝实际区域的定位,从而为公路养护部门提供可靠的数据,以利于其进行公路养护管理[6].即从考虑实际需要而言,对于路面裂缝实际范围定位的意义远远大于断裂裂缝图像的连接等裂缝图像的视觉优化处理操作,产生了“补则余”的现象.
聚类算法广泛应用于裂缝检测领域.1974年Dunn[7]提出模糊 c-均值聚类算法 FCM,此后,很多人对此算法进行了改进,并将其与迭代算法、遗传算法等相结合,提出了迭代聚类算法、遗传算法[8]的模糊聚类算法与FCM算法相结合等算法进行路面裂缝检测.近年来,又有人提出了基于流形距离[9]的聚类算法,并将其广泛应用于路面裂缝的提取中.这些算法都有其应用价值,但是复杂度普遍较高,运算量较大,因此实用性不强.鉴于以上分析的现有路面裂缝识别过程中“不补则错,补则余”的现象,文中提出了最优化中心距离以及角度偏差的双尺度[10]聚类算法路面裂缝识别技术,首先基于系统采集到的路面裂缝3D[11]数据进行了路面三维重构,然后借助聚类算法原理在不修补断裂裂缝的前提下定位裂缝区域,避免了“补则余”现象,并利用杠杆原理准确定位裂缝中心,使用椭圆模型表征聚类后的裂缝范围,避免了“不补则错”的现象,高效实现了路面裂缝双尺度聚类检测,最后进行了路面裂缝类别判断以及网状裂缝路面破损程度因子分析.
1 路面裂缝的双尺度聚类算法检测
聚类[12]就是把一个没有类别标记的样本集事物间的相似性作为类属性划分成若干个子集,使得类内相似度高,类间相似度较小.狭义理解,图像的分割就是聚类,采用不同的图像分割技术使得目标区域与背景区域分开,提取目标区域,即目标区域属于一类,背景属于另一类.广义而言,归类不同区域,或者忽略细节信息仅定位目标区域的“分割”算法都属于聚类算法.聚类算法用于图像分割领域具有很大的应用前景.不同的聚类算法按其聚类准则的不同,可分为“硬[13]”聚类和“软”聚类.就简单的“硬”聚类而言,令集合C表示图像灰度值数据集,对其进行聚类分析相当于将其按一定的准则分割为子区域C1,C2,C3,…,CK,K 为类别数,使得子区域满足条件:
1)非空性 Ci≠Ø(i=1,2,3,…,K);
2)完整性 C1∪C2∪C3∪…∪CK=C.
聚类算法实质是对原始数据再分配,通过挖掘数据内部结构,不断寻找更加优化的聚类算法,从而使得再分配后的数据体现某种内部一致性,这种一致性的体现通常又由特定的准则函数衡量,使用不同的准则函数[14]将得到不同的结果,优化准则函数便是优化聚类算法的一个方向.常用的聚类算法有分层聚类算法、混合解析模式查询算法、最近邻域聚类算法、模糊聚类算法、人工神经网络聚类算法、遗传聚类算法等.纵观这些聚类算法,其核心在于“距离”[15]的表示,不同准则下的“距离”体现不同的聚类效果,当然,对于不同的数据集合相应选取不同的准则才能达到较为理想的效果,因此,“距离”的定义尤为关键.
文中提出的双尺度聚类算法采用“先分后聚”的思想,即先进行小块裂缝基本单元[16]的划分,进行基本单元局部研究,从裂缝椭圆模型基本单元的大小、相对位置等进行分析,使用中心距离以及角度偏差的双尺度聚类准则对小块断裂基本单元进行双尺度聚类,对断裂进行聚类识别,然后通过聚类后裂缝区域各项参数的求取使用裂缝最小外接椭圆模型表征聚类后的裂缝区域,这样不仅避免了使用计算流形距离造成的数据量大、复杂度高带来的实现困难,而且达到了使用流形距离聚类带来的优点,大大提高了裂缝识别效率.
路面裂缝图像在经过预处理之后获得的二值化图像不可避免地会丢失部分信息,从而造成断裂显示的裂缝图像,使得实际中原本连接的裂缝在图像上显示为断开的裂缝,对于这样的图像使用传统的裂缝识别算法必然会产生错误率较高的结果,而修补裂缝图像对于实际需要而言又显得有点冗余,即所谓的“补则余,不补则错”现象.文中就二值化后的裂缝图像在识别问题展开新的研究并进行相关实验,提出了双尺度路面裂缝检测技术.该技术对采集到的路面裂缝3D数据进行路面三维重构后,主要针对使用Otsu阈值分割[17]算法进行预处理后的路面裂缝图像进行裂缝识别.由于邻域搜索法能够同时检测中心点周围的若干像素,对其进行有效性判定,从而可以用于进行裂缝初始聚类基本单元的确定,即进行聚类前的“分”操作.因此,首先对预处理后的路面裂缝用八邻域搜索法确定聚类的基本裂缝单元.
1.1 裂缝基本单元椭圆[18-19]模型
对于初始聚类基本单元的确定,文中采用八邻域搜索法确定初始聚类单元.设M行N列的数据矩阵表示为
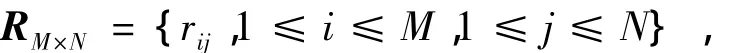

则其数据点的八邻域定义为式中,rij为矩阵中第i行、第j列的元素.
由于裂缝区域的不规则性,为了便于进行严密的数学分析,文中采用裂缝区域的最小外接椭圆模型表征实际裂缝区域,即将八邻域搜索法得到的小块裂缝区域使用其最小外接椭圆模型表征,作为聚类的基本单元.
设路面裂缝图像二值化后第i行、第j列的灰度值为xij,对待聚类区域的数据点使用最小二乘法进行线性拟合,设拟合后的直线为

式中,α、β均为拟合参数.则长轴表示为实际裂缝区域截取拟合直线的长度.设li表示区域内第i个点到拟合直线的距离,短轴为

1.2 裂缝聚类准则函数的确定
准则函数又称价值函数,该函数通过考虑一些关键因子对于结果的影响,基于最大程度体现类内相似度大、类间相似度小的基本原则,同时体现了聚类迭代终止的条件,使得结果逐步优化.文中使用的准则函数同时最优化初始聚类单元的中心距离以及角度偏差的双尺度准则,具体函数原理如下.
准则函数为
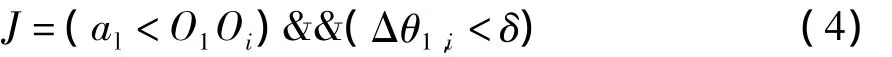
式中:a1为当前聚类中心的所代表的最小外接椭圆的长轴长;O1Oi为待聚类目标的中心到当前聚类中心的距离;Δθ1,i为待聚类目标与当前聚类中心的水平夹角差;δ为正常数,取0o~45o.
该准则函数从角度偏差的要求上体现流形距离的优点,同时又避免了计算流形距离带来的高复杂度,即使用该准则函数聚类可在保持流形距离聚类优点的同时降低流形距离的计算复杂度.
1.3 完整裂缝椭圆模型的确定
使用准则函数对裂缝基本单元进行双尺度聚类后得到的实际裂缝区域需要使用特定模型表征,从而完成裂缝区域的定位.文中使用裂缝区域的最小外接椭圆进行裂缝模型的表征,即对于聚类后的同一裂缝区域使用一个大的椭圆模型表征,显然,该大椭圆需满足:①完全包围属于同一实际路面裂缝的原始裂缝基本单元的椭圆模型;②该大椭圆为其所表征的裂缝区域的最小外接椭圆.关于该区域的定位需要计算特定的参数.其中,对于椭圆模型中心点的定位使用杠杆原理实现.
设O1、O2分别为两个符合聚类准则的两个初始椭圆模型的中心,S1、S2分别表示两个区域的面积,O为聚类后大椭圆的中心点(假设该两椭圆表示的区域满足聚类准则),L1、L2分别表示符合聚类准则的两个初始椭圆模型中心到聚类后椭圆模型中心点的距离,其确定原则使用杠杆原理表示为

聚类前椭圆中心点以及偏转角分别用O1、O2、θ1、θ2表示,聚类后椭圆的长轴、短轴以及偏转角度分别用a、b、θ表示.各项的大小确定如下.
长轴的确定:设聚类前O1、O2的距离为LO1O2,则聚类后椭圆的长轴表示为

偏转角度为

式中,x1、y1、x2、y2分别为椭圆 O1、O2的坐标值.短轴长度为完整裂缝区域到长轴所在直线的最远距离.
1.4 路面裂缝类型及破损程度分析
文中使用提出的圆形度因子进行裂缝类型的判断,圆形度因子表示为

式中,D、B分别表示裂缝椭圆模型的半长轴、半短轴,C即为求得的圆形度因子.C用来作为裂缝类别判断量化参数,依据其大小将裂缝分为线性裂缝、网状裂缝,C越大表示区域越接近圆形,其代表的裂缝区域为网状裂缝;反之,C越小表示裂缝的椭圆模型越扁平,则代表的裂缝为线性裂缝.进一步地,对于线性裂缝可以使用偏转角度的大小将其分为横向裂缝、纵向裂缝.文中选取C>0.3为网状裂缝,C<0.3 为线性裂缝,选取|θ|≥45o为纵向裂缝,|θ|<45o为横向裂缝.另外,对于路面破损,常使用路面破损率(DR)来量化,其求取公式为

式中,Ai为第i类路面的损坏面积,A为调查路面的面积,wi为第i类路面损坏权重.可以看出,不同的i值选取将会获得不同的路面破损率,进而影响到后续路面状况的分析.而i值的选取取决于裂缝类型的判定结果,因此裂缝类型的判定对于路面破损的分析至关重要.
2 路面裂缝的双尺度聚类算法实验
文中首先对3D数据重构后的路面裂缝图像进行了预处理,主要包括使用中值滤波方法进行裂缝图像的滤波去噪以及使用Ostu阈值分割方法进行二值化,得到了二值化后的路面裂缝图像.接下来使用文中提出的聚类算法对二值化后的路面裂缝图像进行了聚类分析,并使用最小外接椭圆框定聚类后的裂缝图像.最后,在获得完整裂缝模型的基础上进行了线性裂缝分级以及网状裂缝路面破损严重程度评价,并进行了误差分析.文中提出的双尺度聚类算法过程如下.
步骤1 按照从上到下、从左到右的顺序扫描预处理后的路面裂缝二值图像;依次以每个数据点作为中心,判断中心点的八邻域是否均为裂缝点,如果是,则八邻域范围内的点属于以该数据点为中心点的基本单元区域,并将每个基本单元区域顺次编号(进行标记),每个基本单元区域均作为裂缝区域.
步骤2 对编号i的裂缝区域中的所有数据点进行线性拟合,得到拟合直线 yi=f(xi1,xi2,…,xini),其中 i=1,2,3,…,ni为编号 i的裂缝区域包含的数据点个数;求出该裂缝区域在对应的拟合直线上截取的线段长度,记为ai;然后计算该裂缝区域内所有数据点到对应的拟合直线的距离,将距离的最大值记为bi,计算ai与水平方向的夹角,记为θi.
步骤3 将每个裂缝区域的参数ai、bi和θi分别作为对应的椭圆的长轴、短轴以及偏转角度,得到每个裂缝区域对应的最小外接椭圆.
步骤4 选取裂缝区域对应的最小外接椭圆中长轴最长的椭圆的中心作为当前聚类中心.
步骤5 选取当前聚类中心对应的裂缝区域之外的所有裂缝区域中编号最小的裂缝区域所在的最小外接椭圆,将其作为待聚类目标.
步骤6 计算待聚类目标的中心到当前聚类中心的距离以及两中心的水平夹角差.
步骤7 判断步骤2得到的距离以及水平夹角差是否满足准则函数(4),若不满足,则结束,否则继续.
步骤8 将该待聚类目标归为当前聚类中心所在的类,将该类中包含的所有椭圆使用一个新的最小外接椭圆进行表征(即将所有椭圆使用一个最小外接椭圆圈在内),分别使用式(3)、(5)、(6)、(7)计算该新的最小外接椭圆的短轴、中心、长轴、以及偏转角,并将该新的最小外接椭圆的中心作为当前聚类中心.
步骤9 判断是否还有未归类的裂缝区域,若有,则继续选取下一个最小编号代表的外接椭圆作为待聚类目标,并返回步骤6;若没有,则继续下一步.
步骤10 将当前聚类中心归为一新类,返回步骤4,否则结束.
2.1 路面裂缝双尺度聚类检测实验
如图1所示为线性裂缝以及网状路面裂缝基于3D数据的三维重构显示图.本系统的基于3D数据的路面三维重构仅用了0.3s的运行时间,可见时间效率较高.
相应的聚类效果如图2、3所示,分别为线性裂缝聚类识别结果及网状裂缝聚类结果的对比图.

图1 路面裂缝3D数据重构显示(运行时间:0.3s)Fig.1 3D reconstruction display of pavement cracks(time:0.3s)

图2 线性裂缝双尺度聚类图(运行时间:0.4s)Fig.2 Two-scale clustering of linear cracks(time:0.4s)

图3 网状裂缝双尺度聚类图(运行时间:0.4s)Fig.3 Two-scale clustering of reticular cracks(time:0.4s)
从对线性裂缝的识别结果可以看出,图3(b)、3(e)中使用八邻域搜索法较为完整地获得了裂缝基本单元的椭圆模型,图3(c)、3(f)中通过双尺度聚类算法判断后得出图3(b)、3(e)中的各个基本裂缝单元属于同一条实际裂缝并使用一个大的椭圆模型表征该实际裂缝,处理速度均为0.4 s,充分体现了文中方法的高效性.文中提出的算法能够获得图3(c)、3(f)所示结果的主要原因在于,该算法在考虑欧式距离为聚类准则之一的同时,使用椭圆模型的偏转角度作为聚类准则之二,间接体现了流形距离考虑到全局一致性的优点.
2.2 路面类别判断及裂缝参数计算
在获得路面裂缝的完整模型后,便可以进行裂缝的类型判断以及参数提取等后续研究.文中使用双尺度聚类算法可以获得完整裂缝椭圆模型的长轴、短轴、偏转角等参数,并将其作为裂缝类型判断的依据;对于网状裂缝,获得裂缝区域断裂裂缝的条数以及聚类后裂缝区域所占椭圆模型的面积,这两个参数可以作为后续路面破损分析的量化指标参考数据.
表1为使用文中提出方法对图2、3所示的裂缝进行参数计算的结果.从表1的结果可以看出,使用文中方法可以获得完整裂缝区域椭圆模型的中心点坐标(像素单位)、半长轴(mm)、半短轴(mm)以及偏转角度.
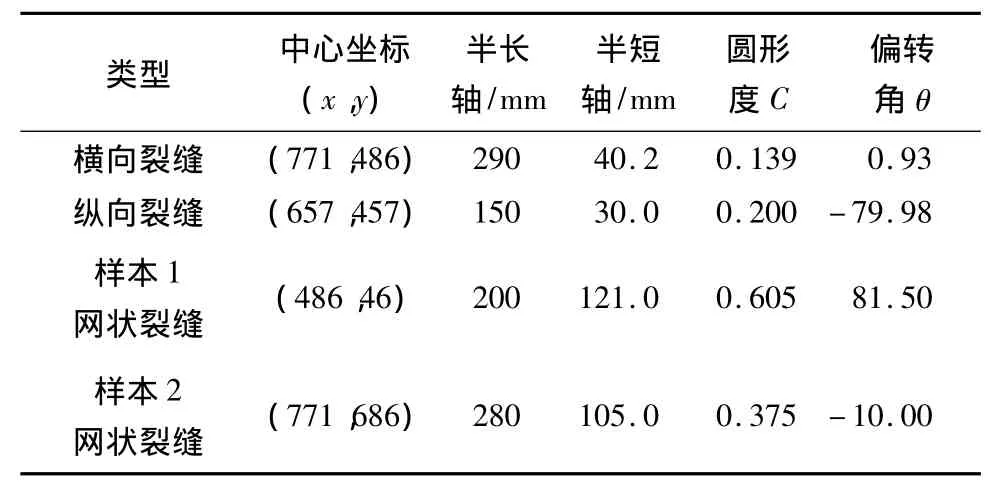
表1 裂缝聚类结果模型参数1)Table 1 Model parameters of crack clustering results
文中对300个路面裂缝样本进行了类别判断并与实测结果进行了对比,结果如表2所示.从表中测量精度的计算结果可以看出,使用文中方法能够以较高的精度获得路面裂缝的分类.对于将圆形度因子作为路面裂缝类型判定具体标准的确定,需要大量的实验样本与人工识别结果进行比对,从而获得固定的量化标准,这可以作为进一步研究的方向.
从表2中实测裂缝分类以及使用文中方法分类结果的对比可以看出,该方法对于网状裂缝具有较高的检测精度,而对线性裂缝的检测精度相对较低.这是由于从人工视觉上分析,人眼对于椭圆的扁平程度(圆形度因子)的敏感程度大于人眼对角度的敏感程度.

表2 不同类型裂缝实测值与文中方法结果的对比Table 2 Comparison between measured values of different types of cracks and those obtained by proposed method
对于网状裂缝,如图3所示,图3(b)、3(e)分别为样本1、2聚类前的裂缝模型,其分别含有3条横向裂缝、7条纵向裂缝,以及1条横向裂缝、5条纵向裂缝、1条网状裂缝.聚类后获得了1条网状裂缝,可见聚类前后裂缝分类结果区别很大,这样会导致路面评价结果的不同.文中从人工测得的136个网状裂缝样本中随机选取100个样本进行了聚类实验,并选取了任意50个样本数据统计了其聚类前后每1幅裂缝图像含有的横向、纵向、网状裂缝的条数,结果对比如图4所示.从中可以看出,聚类后裂缝的条数大大减少.该结果为网状裂缝进一步分析提供了参考量化指标.

图4 每一幅网状裂缝图像聚类前后含有的断裂裂缝条数对比(运行时间:0.3s)Fig.4 Comparison of crack numbers before and after clustering in each crack image(time:0.3s)
3 结语
文中将聚类算法应用于路面裂缝识别领域,综合考虑传统路面裂缝检测技术的在路面裂缝识别中裂缝图像对于预处理后的断裂裂缝图像“补则余,不补则错”的问题,提出了双尺度路面裂缝聚类识别技术,并对不同类型的路面裂缝进行实验研究,获得了较为理想的实验结果.同时,文中提出的双尺度聚类算法路面裂缝识别技术使用最小外接椭圆模型表征裂缝区域,能够在最大程度接近裂缝的同时,将不规则的复杂裂缝转换为数学可表示的图形,便于精确的定量研究,在满足实际需要的前提下大大降低了研究复杂度.另外,聚类准则使用综合考虑了基本裂缝区域中心距离以及角度偏差的双尺度准则,在不失考虑欧式距离的同时,综合体现了流形距离聚类算法的优点,且避免了计算流形距离带来的计算复杂度.文中还提出了使用求取完整裂缝椭圆模型圆形度因子以及偏转角度的方法进行裂缝类别的判断,并进行了误差分析,对网状裂缝进行了聚类前后裂缝条数统计对比,为进一步量化分析提供了参考数据.
[1]Yi Chang Tsal,Kaul V,Mersereau R M.Assessment of pavement distress segmentation methods[J].Journal of Transportation Engineering,2010,136(1):11-19.
[2]徐志刚,赵祥模,宋焕生,等.基于直方图估计和形状分析的沥青路面裂缝识别算法[J].仪器仪表学报,2010,31(10):2260-2266.Xu Zhi-gang,Zhao Xiang-mo,Song Huan-sheng,et al.Asphalt pavement crack detection algorithm based on estimates and shape of the histogram analysis[J].Journal of Scientific Instrument,2010,31(10):2260-2266.
[3]Kelvin WANG C P.Designs and implementations of automated systems for pavement surface distress survey [J].Journal of Infrastructure System,2000,6:24-32.
[4]唐磊,赵春霞,王鸿南,等.基于图像三维地形模型的路面裂缝自动检测[J].计算机工程,2008,34(5):20-21.Tang Lei,Zhao Chun-xia,Wang Hong-nan,et al.Automatic detection of image-based three-dimensional terrain models pavement crack [J].Computer Engineering,2008,34(5):20-21.
[5]张国梁,叶中辰.路面无损检测技术的现状与发展[J].吉林交通科技,2007(3):60-62.Zhang Guo-liang,Ye Zhong-chen.Pavement status and development of non-destructive testing technology[J].Jilin Transportation Technology,2007(3):60-62.
[6]王晓明,冯鑫,党建武.基于多图像与多分辨率的路面裂缝检测方法[J].兰州理工大学学报,2013,39(1):76-82.Wang Xiao-ming,Feng Xin,Dang Jian-wu.Multi-resolution and multi-image based pavement crack detection method[J].Lanzhou University of Technology,2013,39(1):76-82.
[7]Dunn J C.Well-separated clusters and the optimal fuzzy partitions[J].J Cybernet,1974,4:95-105.
[8]白素琴,惠长坤,吴小俊,等.一种基于遗传算法的模糊聚类算法及其与FCM算法的结合[J].华东船舶工业学院学报:自然科学版.2001,12(6):41-43.Bai Su-qin,Hui Chang-kun,Wu Xiao-jun,et al.A genetic algorithm combined with fuzzy clustering algorithm and its relationship with FCM algorithm [J].East China Shipbuilding Institute:Natural Science,2001,12(6):41-43.
[9]王娜,杜海峰,王孙安.一种基于流形距离的迭代优化聚类算法[J].西安交通大学学报,2009,43(5):76-79.Wang Na,Du Hai-feng,Wang Sun-an.An iterative optimization clustering algorithm based on manifold distance[J].Journal of Xi’an Jiaotong University,2009,43(5):76-79.
[10]杨旗,薛定宇.基于双尺度动态贝叶斯网络及多信息融合的步态识别[J].电子与信息学报,2012,34(5):1148-1153.Yang Qi,Xue Ding-yu.Gait recognition based on twoscale dynamic bayesian network and more information fusion[J].Journal of Electronics& Information Technology,2012,34(5):1148-1153.
[11]Kelvin Wang C P.Elements of automated survey of pavements and a 3D methodology[J].Journal of Modern Transportation,2011,19(1):51-57.
[12]王晟.模糊聚类算法的研究与实现[D].南京,南京理工大学计算机学院,2006.
[13]陈树,徐保国.聚类算法模型的研究及应用工[D].无锡:江南大学物联网工程学院,2007.
[14]杨瑞瑞,牛建强,孟红飞.基于流形距离的迭代聚类算法路面裂缝提取[J].计算机工程,2011,37(12):212-214.Yang Rui-rui,Niu Jian-qiang,Meng Hong-fei.Iterative clustering algorithm road cracks extraction method based on manifold distance[J].Computer Engineering,2011,37(12):212-214.
[15]Katakam N.Pavement crack detection system through lo-calized thresholding[D].Bancroft Toledo:The University of Toledo,2009.
[16]Huang Yi-chun,Tsal Yi-chang(James).Crack fundamental element(CFE)for multi-scale crack classification[C]∥7th RILEM International Conference on Cracking in Pavement.Holland:[s.n.],2012:419-420.
[17]吕佩卓,赖声礼,胡蓉,等.基于局部统计特征约束的Snake模型图像分割方法[J].华南理工大学学报:自然科学版,2007,35(9):36-39.Lü Pei-zhuo,Lai Sheng-li,Hu Rong,et al.Image Segmentation Algorithm based on snake model of local statistical characteristic restriction [J].Journal of South China University of Technology:Nartual Science Edition,2007,35(9):36-39.
[18]李秀明,石照耀.基于方程的椭圆轮廓度的评定[J].北京工业大学学报,2009,33(10):1303-1307.Li Xiu-ming,Shi Zhao-yao.Evaluation of ellipse profile based on mathematical equation[J].Journal of Beijing University of Technology,2009,33(10):1303-1307.
[19]王小林,熊新海,张高峰.基于椭圆最小二乘法和圆度轮廓误差评定的椭圆提取方法[J].河南理工大学学报:自然科学版,2008,27(3):294-298.Wang Xiao-lin,Xiong Xin-hai,Zhang Gao-feng.Themethod of ellipse contour extraction based on Leastsquares and elliptic roundness error[J].Journal of Henan Polytechnic University:Naturnal Science,2008,27(3):294-298.

