工艺条件下(1+n)多股流一维传热组织原则优化*
许雄文 刘金平 吴秋丽
(1.华南理工大学 电力学院, 广东 广州 510640; 2.华南理工大学 广东省能源高效清洁利用重点实验室, 广东 广州 510640)
工艺条件下(1+n)多股流一维传热组织原则优化*
许雄文1,2刘金平1,2吴秋丽1
(1.华南理工大学 电力学院, 广东 广州 510640; 2.华南理工大学 广东省能源高效清洁利用重点实验室, 广东 广州 510640)
摘要:在满足多股流换热工艺要求的前提下,分析了一股冷流与多股热流(或者一股热流与多股冷流换热)形成的(1+n)多股流换热过程的最佳组织原则.通过泛函数法,在给定火积耗散条件下求解所需最小换热面积.结果表明:换热工艺条件下,换热过程中保持换热系数的开平方与换热温差的乘积均匀时,(1+n)多股流换热过程最优,所需换热面积最小,而温差场均匀性原则并不是换热器设计的最佳原则.
关键词:换热器;温差;优化
传热过程强化存在两种方向.一是常见的提高换热流体的换热系数,如破坏流动边界层的肋管强化传热[1-2];二是传热过程的组织优化.这类似于一个群体工作效率的提升可以通过提高群体中各个体的工作效率,也可以通过组织各个个体之间的相互协作来实现.文中主要分析传热过程的换热组织优化.
通过组织传热过程来强化传热的最典型例子是逆流传热的广泛应用.众所周知,给定的两股换热流体在给定的换热器中,通过逆流来组织其换热产生的换热量最大,其次是叉流,而顺流换热能力最差.过增元等[3-4]认为造成这种换热能力差别的原因是换热过程中温差场的均匀性不同,换热温差场均匀性越好,换热能力越强,从而提出了换热器设计的场协同原则及温差均匀性原则.为表征温差均匀性,他们还提出了温差均匀性因子的表达式.根据温差场均匀性因子,郜时旺等[5-6]提出了温差场均匀性因子与传热能力的关联式,并验证了在相同的传热单元数及冷热流热容量相同时,温差场越均匀,换热效能越高,并给出了温差场均匀性因子与平均冷凝温度的关系式.
在此基础上,人们陆续开展了多股流换热器内换热组织的研究,提出了各种设计原则和分析方法.20世纪80至90年代,Prasad等[7-11]陆续发表了数篇文章,从不同方面阐述了多股流板翅式换热器的流道排列对其性能、表面温度场、翅片效率和流体分布的影响.刘伟等[12]以Prasad翅片模型为基础,通过数值离散计算来分析板翅式换热器中不同换热通道排列下的温差场均匀性.崔国民等[13-14]通过建立数值求解程序,通过数值法求解多股流的换热过程,并通过求解3个3股流换热算例,得出多股流温差均匀性因子与换热有效度的关系,发现两股流的温差均匀性原则同样适用于多股流换热器,并提出了多股流换热器内各通道温差场最小化的设计原则.吕岩岩等[15]提出了一个无量纲温差的概念,从而改进了这种温差场均匀化因子.Ruan等[16-17]则定义了效能用于描述和分析三股流换热器的热力性能,并通过熵增原理讨论了无量纲设计因子对三股流换热器熵产的影响.Saeid等[18]分别采用子域配置和Galerkim有限元法对顺流和逆流的平行三股流换热器传热微分控制方程进行求解.Shrivastava等[19-20]建立了一个一般性的三股流换热器的理论模型,通过5个工程目标提出了6个无量纲设计因子,并讨论了其对温差场分布设计的影响.Zhao等[21-22]采用交替遗传算法双适应度函数优化多股流板翅式换热器的冷热流通道排列并提出了一种三股流温差场均匀性原则;Wang和Ghosh等[23-24]同样采用遗传算法优化多股流板翅式换热器的冷热流通道排列,Wang还通过实验对优化结果进行了验证.
为表征换热流体之间的换热能力,Guo等[25]提出了火积和火积耗散的概念.程新广[26]将此用于导热问题的优化,提出了导热问题的火积耗散极值原理:对于具有一定约束条件的导热系统,若给定热流边界条件,火积耗散最小时导热过程最优;若给定温度边界条件,火积耗散最大时导热过程最优(热流最大).应用火积耗散极值原理对体点导热问题进行优化,结果表明,在导热区域内,当热导率分布使温度梯度处处均匀时导热过程最优,从而验证了火积耗散极值原理的正确性.朱晓磊等[27]则通过对不同通道排列下多股流板翅式换热器的计算,发现多股流换热器换热量与其火积耗散热阻一一对应,火积耗散热阻越小,换热量越大,因此指出最小火积耗散热阻可用于判定多股流换热过程中通道排列的优劣.
以上关于温差场均匀性原则作为换热器性能判据的研究都只从各种示例中得到验证,没有严格的数学证明.为了得到数学上的严格证明,宋伟明等[28]根据最小火积耗散原理,在给定换热量的前提下推导最小的换热火积耗散,同时还根据给定火积耗散推导最大的换热量.推导结果均表明,换热温差最为均匀时,换热过程最优.对于两股流换热过程而言,这个推导结果是普适的.但是对多股流换热过程来说,以最大换热量为优化目标函数并不合适.因为在实际运行流程中,按照工艺要求,各股热流需要同时得到适当的冷却,各股冷流也需要同时得到加热,不能因为强化换热而牺牲其工艺要求.
单级混合工质(SMR)天然气液化流程中的冷箱换热器[29]如图1所示,图中冷箱为3股流冷箱换热器,“HP-MR-IN”和“HP-MR-O”为高压冷剂进、出冷箱换热器的热流,“LP-MR-IN”和“LP-MR-O”为低压冷剂进、出冷箱换热器的冷流,“NG”和“LNG”表示冷箱换热器的进口天然气和出口液化天然气.按照工艺要求,液化天然气流(LNG)需降温至-160 ℃,因此“LP-MR-IN”冷流的温度需低于-160 ℃.为此,冷流在节流降温之前,即高压冷剂热流在冷箱换热器出口处“HP-MR-O”流也需降至-160 ℃左右.也就是说,要使LNG温度降至-160 ℃,另一股高压冷剂热流也必须降至-160 ℃.此时,若按照给定换热量下最小火积耗散来进行换热优化,可能会导致换热火积耗散最小,但其中一股热流无法获得足够的换热量,从而无法降至所需的温度.如此,整个系统都将无法满足所需的工艺要求.文中在此基础上,在满足工艺要求时对一股冷流与多股热流(或者一股热流与多股冷流换热)形成的(1+n)多股流的换热组织原则进行分析.

图1 单级混合冷剂天然气液化流程冷箱内换热Fig.1 Heat transfer in the cold box of SMR process
1工艺条件下最优温差场组织原则推导
文中就满足工艺要求下的一股冷流与多股热流(或一股热流与多股冷流)一维换热温差场组织问题展开讨论.该问题可转化为:假定一股冷流需与n股热流同时换热,各换热流体的进口状态参数恒定,按照工艺要求,其经换热器后的出口状态参数也是给定的,在此条件下,选择最佳的换热温差场,使得换热所需的面积最小.
根据以上问题描述,换热过程所需总的换热面积为
(1)
式中,K、Q、S、Δt分别表示换热系数、换热量、换热面积和换热温差,下标i表示第i股热流参数,n为热流总数.对于给定进出口参数的各股流,易得

式中,t表示温度,下标c表示冷流的参数.整理可得
(2)


图2 换热多股流温焓图
Fig.2Temperature-enthalpy diagram of the multi-streams with heat transfer
(3)
式中,λ为与Δt无关的常数.由于Z为定值,则求解S的最小值可转变为求解泛函数H的最小值.当H取最小值时,
(4)
则
(5)
若Ki为常数,则将式(5)代入式(2),整理可得
(6)
而根据式(5)可得
(7)
23股流不同温差场组织下的换热过程比较分析
现通过一个例子来说明以上推导结果的正确性.假定有一股冷流需和两股热流进行换热,冷流和热流的参数如表1所示,且保持不变.

表1 换热物流参数Table 1 Parameters of heat transfer streams
按照温差气组织方式不同,定义温差场组织因子θ.令温差均匀性原则下的组织因子为θa,则
θa=Δt.
而上文所述的工艺条件下最优温差场原则对应的组织因子为θb,

另外给定一温差场组织因子θc为
θc=KΔt.
比较分析以上3种传热组织方式下的3股流换热过程.
2.1 计算方法
将换热过程分为3部分,第Ⅰ部分和第Ⅲ部分为两股流换热,而第Ⅱ部分为进出口都可以满足换热组织方式(θ1=θ2)的3股流换热.3部分所需的换热面积分别为SⅠ、SⅡ和SⅢ,则总的换热面积为
S=SⅠ+SⅡ+SⅢ.
为简化换热面积的计算,将换热过程离散成l个微元换热段,假定冷流与不同热流间的换热是间歇性进行的.当θ1,j=θ2,j(j=1,2,…,l)时,冷流与热流1换热,反之,冷流与热流2换热.当l足够大时,这样的换热过程可以等同于两股热流同时与冷流换热.这样处理之后,总的换热面积不用分成3段计算,离散计算程序可大为简化.换热过程所需换热面积计算流程如图3所示.
2.2 结果与分析


图3 换热面积计算流程Fig.3 Calculation process of required heat transfer area


表2 不同换热组织下所需的换热面积Table 2 Required heat transfer area for different heat transfer organizations


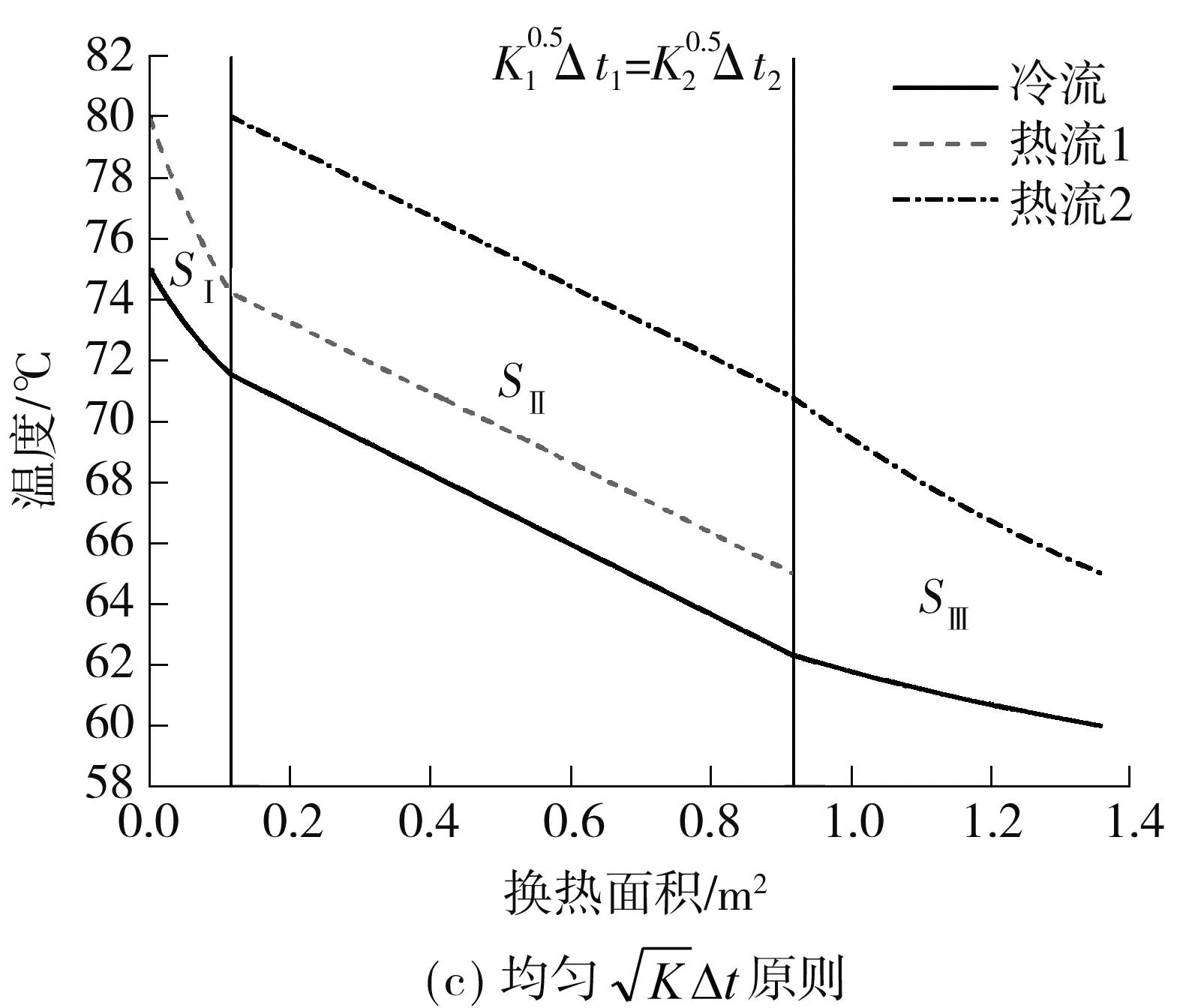
图4 不同传热组织原则下的换热曲线Fig.4 Heat transfer curves with difference heat transfer organization principles
3结论

参考文献:
[1]李若兰,丁杰,霍正齐.管壳式换热器换热管的传热强化 [J].制冷,2013(3):76-81.
Li Ruo-lan,Ding Jie,Huo Zheng-qi.Heat transfer enhancement in shell side of shell and tube heat exchanger [J].Refrigeration,2013(3):76-81.
[2]安恩科,张浏骏,冯祥.间接空气冷凝扩展表面换热器结构优化 [J].制冷,2014(1):70-75.
An En-ke,Zhang Liu-jun,Feng Xiang.Power plant cooling system type slotted aluminum fin surface heat transfer and flow resistance characteristics of numerical study [J].Refrigeration,2014(1):70-75.
[3]过增元.换热器中的场协同原则及其应用 [J].机械工程学报,2003,39(12):1-9.
Guo Zeng-yuan.Principle of field coordination in heat exchangers and its applications [J].Chinese Journal of Mechanical Engineering,2003,39(12):1-9.
[4]Guo Zeng-yuan,Zhou Sen-quan,Li Zhi-xin,et al.Theore-tical analysis and experimental confirmation of the uniformity principle of temperature difference field in heat exchanger [J].International Journal of Heat and Mass Transfer,2002,45(10):2119-2127.
[5]郜时旺,杨沫,危师让.换热器温差场均匀性分析 [J].西安交通大学学报,1999,33(1):51-54.
Gao Shi-wang,Yang Mo,Wei Shi-rang.Study on uniformity of temperature difference field of heat exchanger [J].Journal of Xi’an Jiaotong University,1999,33(1):51-54.
[6]郜时旺,杨沫,徐志明,等.多背压凝汽器中温差场均匀性原则的直接证明 [J].工程热物理学报,1997,18(6):741-743.
Gao Shi-wang,Yang Mo,Xu Zhi-ming,et al.Direct proof of uniformity principle of temperature difference field in multi-pressure condenser [J].Journal of Engineering Thermophysics,1997,18(6):741-743.
[7]Prasad B S V,Gurukul S M K A.Differential method for sizing multistream plate fin heat exchangers [J].Cryogenics,1987,27(5):257-262.
[8]Prasad B S V.The performance prediction of multistream plate-fin heat exchangers based on stacking pattern [J].Heat Transfer Engineering,1991,12(4):58-70.
[9]Prasad B S V,Gurukul S M K A.Differential methods for the performance prediction of multistream plate-fin heat exchangers [J].Journal of Heat Transfer,1992,114(1):41-49.
[10]Prasad B S V.The sizing and passage arrangement of multistream plate-fin heat exchangers [J].Heat Transfer Engineering,1996,17(3):35-43.
[11]Prasad B S V.Fin efficiency and mechanisms of heat exchange through fins in multi-stream plate-fin heat exchangers:development and application of a rating algorithm [J].International Journal of Heat and Mass Transfer,1997,40(18):4279-4288.
[12]刘伟,张卫星,刘志春.场协同下板翅式换热器效率的研究 [J].华中科技大学学报:自然科学版,2007,35(1):77-79.
Liu Wei,Zhang Wei-xing,Liu Zhi-chun.Efficiency study of plate fin heat exchanger with principle of field synergy [J].Journal of Huazhong University of Science and Tehcnology:Nature Science Edition,2007,35(1):77-79.
[13]崔国民,卢洪波,蔡祖恢,等.场协同下多股流换热器换热性能研究 [J].工程热物理学报,2002,23(03):323-326.
Cui Guo-min,Lu Hong-bo,Cai Zu-hui,et al.Study on the heat-transfer property of multi-stream heat exchangers under the effect of field-synergism [J].Journal of Engineering Thermophysics,2002,23(03):323-326.
[14]Cui Guo-min,Lu Hong-bo,Li Mei-ling.Application of even temperature-difference field optimizing principle on fluid organization of multi-stream heat exchanger [C]∥Eighth International Conference on Advanced Computational Methods in Heat Transfer,Heat Transfer VIII.Lisbon:WIT Press,2004.
[15]吕岩岩,崔国民,郭佳,等.多股流换热器设计的量纲1温差场均匀性优化因子 [J].化工学报,2007,58(10):2469-2473.
Lü Yan-yan,Cui Guo-ming,Guo Jia,et al.Application of temperature-difference uniformity optimization principle to path arrangement of multi-stream heat exchangers [J].Journal of Chemical Industry and Engineering (China),2007,58(10):2469-2473.
[16]Ruan D F,Yuan X F,Wu S Y,et al.Exergy effectiveness analysis of three-fluid heat exchanger [J].Journal of Superconductivity and Novel Magnetism,2010,23(6):1127-1131.
[17]Ruan D F,Yuan X F,Li Y R,et al.Entropy generation analysis of parallel and counter-flow three-fluid heat exchangers with three thermal communications [J].Journal of Non-Equilibrium Thermodynamics,2011,36(2):141-154.
[18]Saeid N H,Seetharamu K N.Finite element analysis for co-current and counter-current parallel flow three-fluid heat exchanger [J].International Journal of Numerical Methods for Heat and Fluid Flow,2006,16(3):324-337.
[19]Shrivastava Devashish,Ameel Timothy A.Three-fluid heat exchangers with three thermal communications(part B):effectiveness evaluation [J].International Journal of Heat and Mass Transfer,2004,47(17/18):3867-3875.
[20]Shrivastava Devashish,Ameel Timothy A.Three-fluid heat exchangers with three thermal communications(part A):general mathematical model [J].International Journal of Heat and Mass Transfer,2004,47(17/18):3855-3865.
[21]Zhao Min,Li Yan-zhong.An effective layer pattern opti-mization model for multi-stream plate-fin heat exchanger using genetic algorithm [J].International Journal of Heat and Mass Transfer,2013,60:480-489.
[22]Zhao Min,Li Yan-zhong.New integral-mean temperature difference model for thermal design and simulation of parallel three-fluid heat exchanger [J].International Journal of Thermal Sciences,2012,59:203-213.
[23]Wang Zhe,Li Yan-zhong,Zhao Min.Experimental investigation on the thermal performance of multi-stream plate-fin heat exchanger based on genetic algorithm layer pattern design [J].International Journal of Heat and Mass Transfer,2015,82:510-520.
[24]Ghosh S,Ghosh I,Pratihar D K,et al.Optimum stacking pattern for multi-stream plate-fin heat exchanger through a genetic algorithm [J].International Journal of Thermal Sciences,2011,50(2):214-224.
[25]Guo Zeng-yuan,Zhu Hong-ye,Liang Xin-gang.Entransy-a physical quantity describing heat transfer ability [J].International Journal of Heat and Mass Transfer,2007,50:2545-2556.
[26]程新广.火积及其在传热优化中的应用 [D].北京:清华大学动力工程及工程热物理学,2004.
[27]朱晓磊,张勤,孟继安,等.多股流换热器的火积耗散热阻分析 [J].工程热物理学报,2012,33(12):2040-2041.
Zhu Xiao-lei,Zhang Qin,Meng Ji’an,et al.Analysis of entransy-dissipation-based thermal resistance on multi-stream heat exchanger [J].Journal of Engineering Thermophysics,2012,33(12):2040-2041.
[28]宋伟明,孟继安,梁新刚,等.一维换热器中温差场均匀性原则证明 [J].化工学报,2008,59(10):2460-2464.
Song Wei-ming,Meng Ji’an,Liang Xin-gang,et al.De-monstration of uniformity principle of temperature diffe-rence field for one-dimensional heat exchangers [J].Journal of Chemical Industry and Engineering,2008,59(10):2460-2464.
[29]Xu Xiong-wen,Liu Jin-ping,Jiang Chuan-shuo,et al.The correlation between mixed refrigerant composition and ambient conditions in the PRICO LNG process [J].Applied Energy,2013,102:1127-1136.
Principles of Heat Transfer Organization Optimization for (1+n) Multi-Stream One-Dimensional Heat Exchanger Meeting Process Requirements
XuXiong-wen1,2LiuJin-ping1,2WuQiu-li1
(1.School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Guangdong Key
Laboratory of Efficient and Clean Energy Utilization,South China University of Technology,Guangzhou 510640,Guangdong,China)
Abstract:On the premise of meeting the requirements of the multi-stream heat transfer process,the optimal orga-nization principle of the heat transfer processamong(1+n) multistreams,which comes from one cold stream and multi hot streams or from one hot stream and multi cold streams,is discussed in this paper.Then,a functional analysisis conducted to solve the required minimum heat exchange area under a given entranspy dissipation.The results show that,when the process requirements are met and the product of the heat transfer temperature difference and the square root of heat transfer coefficient is kept uniform,the heat transfer process among (1+n) multi streams shows the best performance with aminimum heat exchange area,and that the principle of keeping the temperature difference (Δt) uniform is not the best.
Key words:heat transfer;temperature difference;optimization
中图分类号:TK 172
doi:10.3969/j.issn.1000-565X.2015.08.002
文章编号:1000-565X(2015)08-0009-06
作者简介:许雄文(1983-),男,助理研究员,主要从事制冷与传热研究.E-mail: epxwxu@scut.edu.cn
*基金项目:中国博士后科学基金资助项目(2014M552195);国家自然科学基金资助项目(51206056);华南理工大学中央高校基本科研业务费专项资金资助项目(D215161w);华南理工大学广东省能源高效清洁利用重点实验室资助项目 (2013A061401005)
收稿日期:2014-08-06
Foundation items: Supported by the China Postdoctoral Science Foundation(2014M552195) and the National Natural Science Foundation of China(51206056)

