有限点法在液舱晃荡问题中的应用*

卢雨　胡安康,2†　刘亚冲

(1.哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001； 2.中集船舶海洋工程设计研究院，上海 201206)

有限点法在液舱晃荡问题中的应用*

卢雨1胡安康1,2†刘亚冲1

(1.哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001； 2.中集船舶海洋工程设计研究院，上海 201206)

摘要：液舱晃荡问题是近年来液货船设计中十分关注的问题之一，它涉及自由液面的大幅运动等一系列强非线性问题，因此给基于欧拉观点下空间拓扑网格的数值模拟带来了较大的难度.文中基于拉格朗日观点下的有限点法(FPM)，对不同充容率的液舱晃荡问题进行了数值模拟，并将数值计算结果与试验值进行对比验证.结果表明：当激励频率与液舱固有频率一致时，舱内流体的晃荡较为剧烈；而当充容率不同时，舱壁对液体流动的抑制作用使得高充容液舱内的流体翻卷变形较为平缓.通过有限点法有效且准确地模拟了不同充容率液舱在各激励频率下的水面晃荡情况，与试验现象基本吻合.同时通过对舱壁监测点的压力计算得知，有限点法的数值结果与实测压力曲线基本保持一致.FPM针对不同工况下的二维液舱晃荡情况均给出了较为准确的数值模拟结果，有效验证了有限点法的可靠性.

关键词：液舱晃荡；拉格朗日观点；有限点法；移动最小二乘法；泊松方程

近年来，液货船在船舶交易市场中的需求不断增长，显著刺激了船舶运输技术的不断提高.液货船的关键技术之一就是液舱内流体的晃荡问题.常见的晃荡现象有：驻波、行进波、水跃和组合波，还伴有水跃、翻卷等强非线性现象.而液体晃荡产生的冲击压力会严重威胁到舱壁以及船体结构的安全性能，并在一定程度上影响航行中船舶的稳性，强烈的晃荡将直接导致严重的海洋结构物的破坏[1-2]，因此液舱晃荡研究已在全世界范围内受到越来越多的关注.

液体晃荡是一种高度非线性的复杂流动现象，这种非线性来源于自由液面的大幅度运动、湿边界的变化以及流固耦合等因素，严重阻碍了问题的理论研究.随着计算机技术的迅猛发展，数值模拟技术成为研究液舱晃荡问题的重要手段.Armenio[3]采用改进 MAC (Marker-And-Cell) 方法(即标记子与单元方法)将流体压力和速度作为求解变量，成功地求解了带有自由面的流体大幅晃荡问题.Kim等[4-6]基于有限差分法数值模拟了液舱晃荡运动，Hu等[7]采用约束插值轮廓法(CIP)研究了剧烈液舱晃荡现象.祁江涛等[8]采用两相流 VOF (Volume of Fluid) 法，结合动网格技术，针对二维及三维液舱晃荡情况进行了数值计算.沈猛等[9-10]改进了传统VOF法，基于部分单元参数概念，引入了一种混合自由表面边界速度条件的基本原理，解决了具有复杂边界的液舱晃荡问题.方智勇等[11-12]依据Level-set法隐式跟踪运动界面原理，数值模拟了由箱体做简谐运动引起的液舱晃荡问题，证明了此法的可行性.然而这些 CFD (Computational Fluid Dynamics) 技术在处理液舱晃荡问题时往往是基于空间网格拓扑结构，极易造成数值扩散导致捕捉液面模糊等问题，并且很难模拟出液体飞溅、融合等复杂自由表面流现象，因此这些基于欧拉观点的数值求解技术在处理大变形的流体运动方面遇到了一些难以克服的问题.

在处理流体复杂变形的问题上，相比于传统欧拉观点的网格类方法，基于拉格朗日观点发展而来的无网格粒子法受到众多学者的青睐[13].有限点法Finite Point Method,FPM) 是近些年发展起来的新型Lagrange法，是一种真正意义上的无网格技术.它首先由西班牙学者Oate等[14]于1996年提出，用有限空间粒子点来离散表达流体域，不受固定网格结构形式的束缚，每个粒子点携带特定的物理信息，如速度压力等，粒子间的相互作用通过移动最小二乘法近似得到，这样就较为容易地构造出所期望的顺序一致性，并基于配点法离散求解流体运动控制方程，达到时刻监测粒子运动状态并准确追踪粒子运动轨迹的效果.此外有限点法对于边界的处理采用较为通用的边界粒子分布法，易于数值实现.FPM在数值求解与液面捕捉方面的灵活性，使其被应用到许多流动问题的求解.早年Oate等[15]基于该有限点法, 对不可压缩流体运动问题进行了数值研究.随后Oate等[16]将FPM应用于求解结构力学中的弹性力学问题，并在线弹性结构分析中取得了一定的进展.2005年，Shu 等[17]基于无网格法中的离散原理及局部等参插值理论，提出了一种新型无网格法-等参有限点法(IFPM)，并将用于其求解粘性不可压缩流等问题，得到了满意的结果.之后，Pandey 等[18]利用有限点法数值求解了热力学流动中的 LLNS (Landau-Lifshitz Navier-Stokes) 方程，并与理论值进行有效性验证，结果吻合较好.2014年，Reséndiz 等[19]利用泰勒级数形式的有限点法对二维热传导问题进行研究，并与解析解对比，得到了满意的精度.由此可见，有限点法的研究已受到各国学者的重视.

文中基于有限点法对液舱晃荡问题进行了数值模拟，对流体大幅运动特性、舱壁周期性砰击压力以及液面大变形进行了分析.主要采用投影法对不可压缩Navier-Stokes方程进行求解，压力泊松方程中的空间导数由移动最小二乘法近似获得.文中选用新四次函数作为计算的权函数，是因为新四次函数是一条连续曲线，且二阶导数曲线具有较好的光滑性，可光顺连续地描述大变形自由面.最后通过数值计算结果与试验值的对比，对有限点法在求解液舱晃荡问题中的可靠性进行了验证.

1数值方法

1.1　控制方程

不可压缩流体的运动控制方程(质量守恒、动量守恒)表述为

(1)

(2)

式中，ρ为流体密度, ui为坐标系中对应i轴的速度分量, xi为对应i轴的方向分量，p为压力，μ为流体的动力粘性系数，fi为源项(通常取重力加速度gi).由于是从拉格朗日观点出发，故式(1)和式(2)右端的时间导数项是以物质导数的形式给出.

1.2　投影法

(3)

(4)

(5)

式(5)中增加了压力梯度项，通过引入不可压缩流体的连续方程，可显式获得关于压力的泊松方程，即为

(6)

将式(5)沿边界Γ的外单位法向量n投影，得到关于压力p的Neumann 边界条件，即

(7)

1.3　压力泊松方程的导数离散

在投影法求解压力泊松方程过程中，产生了压力项的方向导数及Laplacian算子.本节利用移动最小二乘法的思想，将空间任意点的待求函数导数用支持域内的周围粒子信息来近似表达.

首先令流场中全部粒子点(粒子总数为n)的函数向量为U=[u1(x),u2(x),…,un(x)]，u(x)为任意粒子点x处的待求函数，则其近似函数u(x)可表示为

(8)

式中:b(x)T=[b1(x)b2(x)…bk(x)]，bi(x)为基函数，k为基函数的个数；a(x)T=[a1(x)a2(x)…ak(x)]，ai(x)为待定系数.文中计算取二维空间单项式基函数:

b(x)T=[1xyx2xyy2],k=6

(9)

考虑其计算通用性，将基函数bi(x)写入全局矩阵中，即

(10)

根据最小二乘法求取极值原理，可得如下关系:

S(x)a(x)=r(x)

(11)

其中S(x)=VW(x)VT，r(x)=VW(x)U，W(x)为权函数矩阵，即

(12)

分别对式(11)两边求一阶及二阶导数，可得

a′=S-1(r′-S′S-1r)

(13)

a″=S-1((r″-S″S-1r)-2S′S-1(r′-S′S-1r))

(14)

根据式(13)可得近似函数的一阶导数:

(∏u)′=(b′)Ta+bTa′=

(b′)TS-1r+bTS-1(r′-S′S-1r)

(15)

联立式(13)与(14)可得其近似函数二阶导数:

(∏u)″=(b″)Ta+2(b′)Ta′+bTa″=

(b″)TS-1r+2(b′)TS-1(r′-S′S-1r)+

bTS-1((r″-S″S-1r)-2S′S-1(r′-S′S-1r))

(16)

借助式(16)及(17)，即可离散压力泊松方程，最后形成关于压力的大型稀疏矩阵，采用较为通用的双共轭梯度稳定法(Bi-ConjugateGradientsStabilizedMethod)[20]来迭代求解，并设定迭代前后时间步内的压力误差限作为计算收敛条件.同时为满足Dirichlet条件，在计算开始时需指定每个粒子点的初始压力.

文中计算权函数w(x)选取新4次权重函数，因为该函数本身是1条连续曲线，且2阶导数曲线具有较好的光滑性.具体取为

(17)

式中，d=x-xi，h为支持半径.

1.4　自由面判断

FPM 对自由液面的判断采用粒子数密度的概念来区分自由液面与内部流体粒子，当粒子数密度〈ni〉满足：

〈ni〉<βn0

(18)

即可判定为自由面粒子，其中n0为初始粒子数密度.在求解压力 Poisson 方程时，自由面粒子的压力赋值为 0.β是一参数，对自由面的判断有一定的影响, 一般取值为β=0.80~0.99.

2数值算例

为验证文中提出的有限点法的有效性，依据文献[21]中的试验，选取4个不同工况的液舱晃荡模型(见表1)，对其进行数值模拟.同时在计算中设置压力监测点O，以便与试验中测得的舱壁压力进行对比，定量分析数值计算结果的准确性.

表1　液舱晃荡计算工况Table 1　Calculation conditions of tank sloshing

液舱晃荡计算模型与试验[21]保持一致，取二维矩形舱，宽度为0.6 m，高度为0.3 m.液体的晃荡由液舱做规则横荡运动激发产生，其表达式为

(19)

式中：A为运动幅值；Amax为振幅，取值0.05 m.具体计算模型见图1.

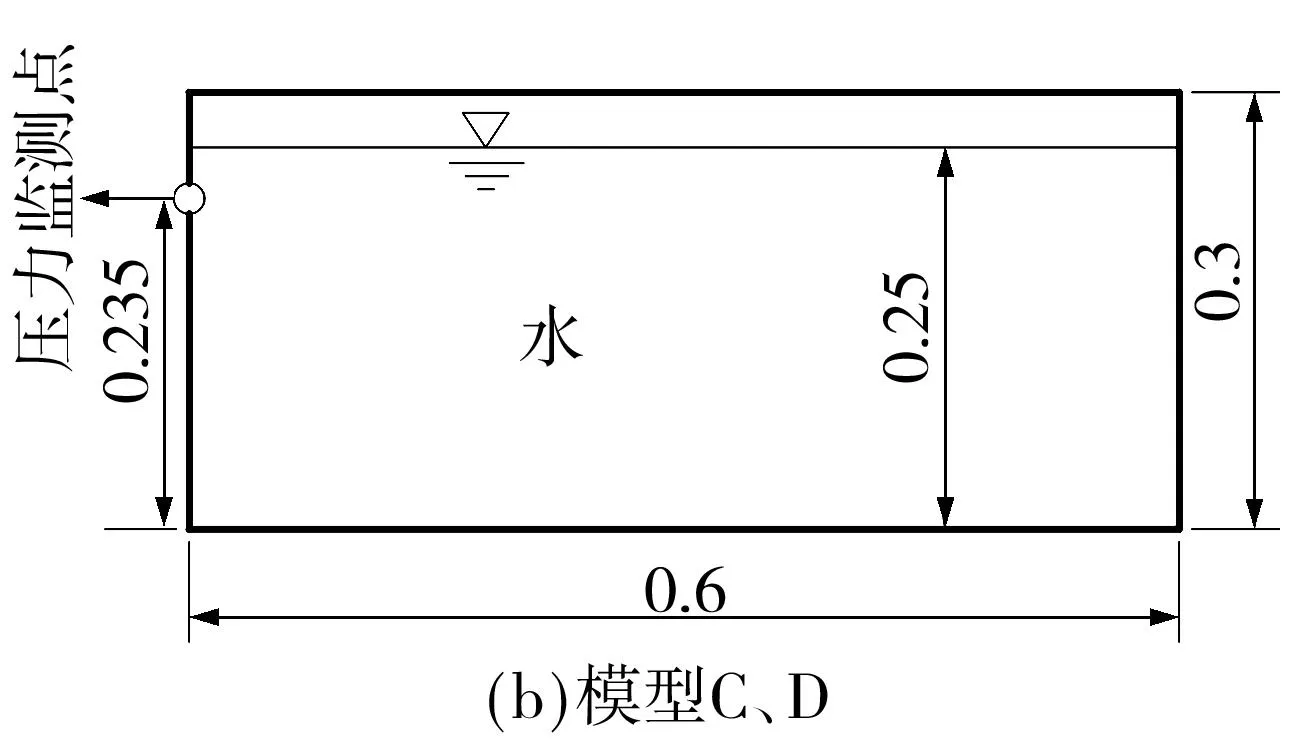
图1　液舱模型及模拟工况示意图(单位：m)Fig.1　Schematic sketch of the liquid tank models and simulation conditions(Unit:m)

计算中物理参数的设置为：水的密度为 1 000 kg/m3，运动粘性系数取 1.0×10-6m2/s，重力加速度为 9.81 m/s2，粒子支持域半径为 0.007 m，时间步长取为0.001 s，计算中分别数值模拟了10个周期的晃荡运动.

2.1　晃荡模型A

在晃荡模型A中，液舱充容率40%为中等充容，激励频率小于共振频率.图2为晃荡模型A在一个周期内的不同时刻(t=0.1T，0.2T，0.3T和0.4T)运动流场的计算结果，以压力分布的形式给出.由图2可看到，在t=0.1T时, 液舱内流体在激励力的作用下向右侧壁运动，并伴有行进波.当达到 0.2T时，撞壁流体在惯性的作用下开始沿壁面上升.当t=0.3T时, 沿右侧壁面运动的流体再次撞击到液舱顶棚，同时底部的液体由于越积越多，并在液舱的激励运动下愈要形成反向运动的“水包”.当接近 0.4T时，抨击右侧壁面的流体以凸起“水包”状开始向舱壁左侧运动.在舱壁激励力的作用下，流体发生了不同形态的晃荡，出现了行进波、水跃、翻卷等强非线性现象.这些复杂变形的水面通过FPM得以准确表达，相比于传统基于空间网格的数值模拟方法，有限点法不但消除了对流项的数值耗散问题，还具有较强的自由面捕捉能力，这对自由面大幅运动的类似求解方法具有一定的指导意义.

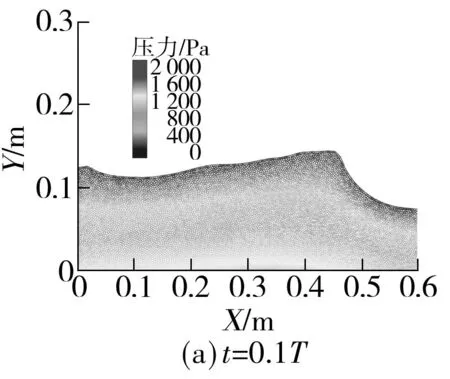
图2　模型 A 在不同时刻的运动流场示意Fig.2　Numerical results of liquid sloshing case A at different time

为定量分析FPM在求解液舱晃荡问题时的准确性，图3给出了压力监测点O在不同时刻的试验测量值[21]与数值结果.由图3可知，数值计算的压力峰值产生了一定幅度的非物理震荡，前4个周期内压力峰值较试验值偏大.对第1个周期内的两条曲线进行对比分析可知，试验测量峰值(1 300 N/m2)约为数值计算峰值(2 400 N/m2)的1/2.在之后的周期内，数值计算结果与试验测量值基本保持一致.对比两条曲线可知，每个周期内均有两个压力峰值，且第2峰值的数值结果与试验值基本相同，压力的整体变化趋势基本吻合，从定量角度验证了FPM对解决液舱晃荡问题具有很好的可靠性.

图3　模型A监测点O压力计算结果与试验值对比

Fig.3 Pressure comparison between calculation and experiment for measuring pointOof case A

2.2　晃荡模型B

晃荡模型B为中等充容，同样液舱充容率为40%，激励周期为1.3 s.图4列出了试验[21]与数值场结果在4个时刻(t=0.1T，0.2T，0.3T和0.4T)的流场对比，其中数值计算的瞬时流场同样以压力形式给出.从图4可看到，由于激励频率与共振频率相同，液舱的横荡运动激发液体发生剧烈的晃荡，自由液面凹凸明显；尤其当t=0.2T时, 靠近液舱右侧壁的流体压强激增，形成较大的压力梯度.当达到0.4T时，由于顶部与左侧舱壁与液体发生强烈的拍击，促使流体翻卷下落，并伴有迸溅的水花.通过将数值解与试验图像定性对比可知，这些复杂变形通过有限点法得到了准确的捕捉，且与试验结果吻合较好，验证了FPM在解决液舱晃荡问题中的可靠性.

图4　模型 B 在不同时刻(t=0.1T，0.2T，0.3T和0.4T)的运动流场试验对比Fig.4　Qualitative comparison between FPM and experiment att=0.1T, 0.2T, 0.3Tand 0.4T, Case B-sloshing in medium-filling tank

2.3　晃荡模型C

在前面的晃荡模型A、B中，讨论的是液舱中等充容情况，下面给出高充容率的液舱晃荡计算结果.晃荡模型C中的充容率高达83%，图5为试验[21]与数值结果在4个时刻(t=0.02T，0.17T，0.35T和0.50T)的流场对比，其中数值结果同样以压力场形式给出.从图5可看到，在t=0.02T时，液舱的激励作用使得流体开始做晃荡运动，水面呈凹陷状.在接近t=0.17T时，液舱内运动流体逐渐靠近右侧舱壁，并伴有飞溅的液滴.直到t=0.35T时，由于右侧壁面的阻挡, 在惯性的驱使下，使得撞击到右侧舱壁的液体沿壁面上升，并再次与上壁面发生拍击.当达到t=0.50T时，沿上壁面运动的流体由于受到重性力的作用，开始下落, 并与从底部向上运动的水流汇集，融合的水面发生极复杂的变形.观察整个运动过程，由于液舱的充容率很高，其横荡运动使得流体与左右舱壁发生了强烈的拍击，液面变化更加明显，其剧烈程度明显高于中等充容模型.通过与试验图片的对比可知，数值模拟结果与试验值基本吻合，说明有限点法对解决高充容率的液舱晃荡具有很好的数值模拟能力.

图5　模型 C 在不同时刻(t=0.02T，0.17T，0.35T和0.50T)的运动流场试验对比Fig.5　Qualitative comparison between FPM and experiment att=0.02T, 0.17T, 0.35Tand 0.50T, Case C-slo-shing in high-filling tank

2.4　晃荡模型D

晃荡模型D与晃荡模型C的充容率相同，但激励周期为1.0 s.本晃荡模型的计算是为了从定量角度出发，来验证有限点法在数值计算高充容液舱晃荡问题时的准确性.为与试验[21]保持一致，计算中的压力监测点O高度为0.235 m.下面给出晃荡模型D中压力监测点在不同时刻的试验值[21]与数值结果，详见图6.

图6　模型D监测点O压力计算结果与试验值对比Fig.6　Measuring pointOof case D pressure comparison in between calculation and experiment

由图6可知，压力数值计算峰值较实测压力值略有偏大.分析其原因主要是由于数值模拟时采用的是单相流，而在真实试验中当晃荡流体撞击到壁面时，由于下落、翻卷、融合的过程中融入一定组分的空气，促使流体的拍击压力起到了缓冲作用，造成计算结果大于试验值.从压力的相位角度观察，图中前几个周期内有一定的相位差存在，随着时间的推移，相位差基本消除，峰值也渐趋保持一致.总体来说，数值结果与试验基本吻合，说明FPM对于液舱晃荡问题的求解具有较好的准确性.

3结语

文中采用有限点法对不同充容率的二维液舱在不同频率下的受迫运动进行了数值模拟研究.结果表明：当激励频率与液舱固有频率一致时，舱内流体的晃荡较为剧烈；而当充容率不同时，由于舱壁对液体流动的抑制作用，使得高充容液舱内的流体翻卷变形较为平缓.通过有限点法准确有效地捕捉到液舱在不同激励频率下的复杂水面晃荡情况，如水跃、翻卷以及融合等强非线性现象，FPM均给予较为准确的模拟，与试验现象基本吻合.与此同时，在晃荡模型B和D中，通过分析监测点的压力曲线，进一步验证有限点法在定量分析上也有满意的精度.由于模型D为高充容状态，相对模型B而言，空气组分影响较小，所以模型D中压力曲线更为准确.为提高数值模拟精度，今后可在FPM法中采用多相流模型.纵观定性对比与定量分析，有限点法在解决不同工况的二维液舱晃荡问题时均得到较为准确的模拟结果，说明其在求解液舱晃荡问题中是可靠、有效的.

参考文献：

[1]Pitblado Robin M,Woodward John L.Highlights of LNG risk technology [J].Journal of Loss Prevention in the Process Industries,2011,24(6):827-836.

[2]Pistani Fabrizio,Thiagarajan Krish.Experimental mea-surements and data analysis of the impact pressures in a sloshing experiment [J].Ocean Engineering,2012,52(1):60-74.

[3]Armenio V.An improved MAC method (SIMAC) for unsteady high-reynolds free surface flows [J].International Journal for Numerical Methods in Fluids,1998,24(2):185-214.

[4]Kim Y.Numerical simulation of sloshing flows with impact load [J].Applied Ocean Research,2001,23(1):53-62.

[5]Kim Y,Shin Y S,Lee K H.Numerical study on slosh-induced impact pressure on three-dimensional prismatic tanks [J].Applied Ocean Research,2004,26(5):213-226.

[6]Kim Y,Nam B W,Kim D W,et al.Study on coupling effects of ship motion and sloshing [J].Ocean Engineering,2007,34(16):2176-2187.

[7]Hu C H,Yang K K,Kim Y H.3-D numerical simulations of violent sloshing by CIP-based method [J].Journal of Hydrodynamics:Ser B,2010,22(5):253-258.

[8]祁江涛，顾民，吴乘胜.液舱晃荡的数值模拟 [J].船舶力学，2008,12(4)：574-581.

Qi Jiang-tao,Gu Min,Wu Cheng-sheng.Numerical simulation of sloshing in liquid tank [J].Journal of Ship Mechanics,2008,12(4)：574-581.

[9]沈猛.基于改进VOF法的棱形液舱晃荡分析及应用 [D].上海：上海交通大学船舶海洋与建筑工程学院，2008.

[10]沈猛，王刚，唐文勇.基于改进VOF法夫人棱形液舱液体晃荡分析 [J].中国造船，2009,50(1):1-9.

Shen Meng,Wang Gang,Tang Wen-yong.Liguid sloshing analysis on prismatic tanks based on improved VOF method [J].Shipbuilding of China,2009,50(1):1-9.

[11]方智勇，杨松林，朱仁庆.Level-set法在液体晃荡研究中的应用 [J].水动力研究与进展，2007,22(2):150-156.

Fang Zhi-yong,Yang Song-lin,Zhu Ren-qing.Application of Level-set method in the research on liquid sloshing [J].Journal of Hydrodynamics,2007,22(2):150-156.

[12]方智勇，端木玉，朱仁庆. 基于Level-set 法的液舱液体晃荡数值模拟 [J].船舶力学，2007,11(1):62-67.

Fang Zhi-yong,Duan Mu-yu,Zhu Ren-qing.Numerical simulation of liquid sloshing in a liquid tank based on Level-set method [J].Journal of Ship Mechanics,2007,11(1):62-67.

[13]赵相坤，李凤霞，战守义.基于GPU的面向SPH流体模拟的邻居查找算法 [J].华南理工大学学报:自然科学版，2011,39(7)：150-155.

Zhao Xiang-kun,Li Feng-xia,Zhan Shou-yi.CPU-based neighbor search algorithm for SPH fluid simulations [J].Journal of South China University of Technology:Natural Science Edition,2011,39(7):150-155.

[17]Shu C,Ding H,Chen H Q,et al.An upwind local RBF-DQ method for simulation of inviscid compressible flows [J].Computer Methods in Applied Mechanics and Engineering,2005,194(18-20):2001-2017.

[18]Pandey A,Klar A,Tiwari S.Meshfree method for fluctuating hydrodynamics [J].Mathematics and Computers in Simulation,2012,82(11):2157-2166.

[19]Reséndiz-Flores E O,García-Calvillo I D.Application of the finite pointset method to non-stationary heat conduction problems [J].International Journal of Heat and Mass Transfer,2014,71:720-723.

[20]Gu T X,Zuo X Y,Liu X P,et al.An improved parallel hybrid bi-conjugate gradient method suitable for distributed parallel computing [J].Journal of Computational and Applied Mathematics,2009,226(1):55-65.

[21]Kishev Z R,Hu C,Kashiwagi M.Numerical simulation of violent sloshing by a CIP-based method [J].Journal of marine science and technology,2006,11(2):111-122.

Application of Finite Point Method to Liquid Sloshing in Tanks

LuYu1HuAn-kang1,2LiuYa-chong1

(1.College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China;

2.CIMC Ocean Engineering Design & Research Institute Co., Ltd., Shanghai 201206, China)

Abstract:In recent years, the structural design of liquid cargo ships has been focused on the liquid sloshing in tanks, which involves the high non-linearity problem related to the large amplitude motion of free liquid surface and therefore causes some difficulties in Euler numerical simulation depending upon spatial topological meshes. In this paper, the liquid sloshing of a tank at different filling ratios is numerically simulated by means of the Lagrangian view-based finite point method (FPM), and the numerical results are compared with the experimental ones. The results show that when the excitation frequency is consistent with the natural frequency of the tank, the fluid sloshing is severer; and that, at different filling ratios, the fluid in the tank with a high filling ratio will flow with mode-rate deformations due to the inhibition of bulkheads. Moreover, the FPM can effectively and accurately simulate the violent changes of the liquid sloshing of the tank at different filling ratios under the multi-frequency excitation, and the simulation results accord well with the experimental phenomena. Meanwhile, an impact pressure on the bulkheads is observed and the calculated values obtained through the FPM are consistent with the measured pressure curves. It is, therefore, found that the FPM performs accurate simulations on the two-dimensional liquid sloshing in the tank under different conditions, which effectively verifies the reliability of the FPM.

Key words:liquid sloshing in tanks; Lagrangian view; finite point method; moving least square; Poisson equation

中图分类号：U661.1

doi:10.3969/j.issn.1000-565X.2015.08.021

文章编号：1000-565X(2015)08-0144-07

作者简介：卢雨(1988-)，男，博士生，主要从事船舶流体力学研究.E-mail： luyu90627@126.com†通信作者： 胡安康(1956-)，女，博士，教授，主要从事船舶总体设计理论与方法研究.E-mail： ankang.hu@cimc.com

*基金项目：国家自然科学基金资助项目(51379040)

收稿日期：2015-01-12

Foundation item: Supported by the National Natural Science Foundation of China(51379040)