三相四线制系统3D-SVPWM调制策略优化设计*
王裕 刘翔 谢运祥
(华南理工大学 电力学院, 广东 广州 510640)
三相四线制系统3D-SVPWM调制策略优化设计*
王裕刘翔谢运祥
(华南理工大学 电力学院, 广东 广州 510640)
摘要:在深入分析传统三维空间矢量脉宽调制(3D-SVPWM)算法的基础上,证明传统调制算法在运算过程中是可以简化的,并由此对传统调制算法进行改进,提出优化的3D-SVPWM调制算法.采用所提出的优化3D-SVPWM调制算法,可以在保证系统效果和性能的前提下对传统调制算法进行大幅简化,有效降低调制算法的复杂度和计算量,提高调制算法的稳定性和实时性,减轻系统的软件负荷,为系统控制算法的改良和升级提供更多的可操作空间.通过在三相四线制电容中分式有源电力滤波器中的仿真和实验,验证了所提出算法的可行性与优越性.
关键词:三维空间矢量脉宽调制;简化算法;有源滤波器
电压空间矢量脉宽调制(SVPWM)和正弦脉宽调制(SPWM)为两种常用的变流调制方式[1].SVPWM 是把三相变流器的指令输出电压在复平面上合成为电压空间矢量,并通过不同的开关矢量组合去逼近指令电压空间矢量,与传统的 SPWM 相比,其开关器件的开关次数可以减少1/3,直流电压的利用率可提高15%,能获得较好的谐波抑制效果,且开关频率固定,控制精度高,易于实现数字化控制[2-4].由于其优点显著,SVPWM 算法已被广泛用于各种功率变换器中,如逆变器、整流器、有源电力滤波器、静态同步补偿器等[5-8].
近年来,国内外许多学者对SVPWM算法进行了深入研究,提出了许多算法改进策略.然而,这些研究成果大多都集中在 2D-SVPWM 调制算法上[9-14],针对 3D-SVPWM 进行优化和改进的并不多.在已有的改进 3D-SVPWM 算法的文献中,文献[15]中提出一种新型的 3D-SVPWM 算法,直接比较由三相电压经过线性运算获取的中间变量来判断参考电压矢量所在三棱柱,再根据参考电压矢量的分量判断所在四面体,并根据中间变量的线性组合直接获取基矢量的作用时间.文献[16]中提出了一种基于abc坐标的 3D-SVPWM 算法,避免了因αβγ坐标变换而带来的计算复杂化问题.文献[17]通过分析三相电压和四面体、开关矢量之间的关系,简化导通时间的计算过程,并省去了如查表等不合理的操作,减轻了处理器的负担.文献[18]中提出将四面体和截面计算放在一个公式进行,并且开关矢量的导通时间由一个只含有0和1的矩阵给出,简化了计算过程.
虽然上述研究对 3D-SVPWM 调制算法进行了一定程度的改进,但由于仍存在空间矢量扇区判断、空间矢量占空比计算等过程,算法仍显复杂,计算量仍然很大,这将耗费大量的计算时间和软件资源,降低系统的实时性,并导致系统控制算法的应用和升级受到很大的限制.因此,3D-SVPWM 调制算法仍然有可以深入研究的空间.
为了克服算法仍然存在的不足,文中提出一种优化的 3D-SVPWM 调制算法.在深入分析和推导传统 3D-SVPWM 调制算法的基础上,证明传统算法在其运算的过程中是可以省略的,并由此对传统3D-SVPWM 调制算法进行简化和改进.采用优化的调制算法,可以在保证系统性能的前提下大幅简化调制算法,有效降低算法的复杂度和系统的软件负荷,提高算法的稳定性和实时性,为系统其他部分的控制算法提供更多的可操作空间.通过在三相四线制电容中分式有源电力滤波器(APF)的仿真和实验,验证了所提出方法的可行性与优越性.
1优化的3D-SVPWM调制算法推导
以 3D-SVPWM 算法在 APF 上的应用为例,APF 的控制目标是通过检测负载电流中的谐波分量作为参考电流,控制逆变器中开关管的通断,产生相应的补偿电流抵消负载电流中的谐波分量,从而抑制负载电流中的谐波分量注入电网,以免造成谐波污染[19-20].三相四线制并联型电容中分式 APF 的主电路如图 1 所示.图中,Usa、Usb、Usc为三相电源电压,Isa、Isb、Isc为三相电源电流,非线性负载为三相不控整流桥接纯电阻RL,ILa、ILb、ILc是由非线性负载引起的负载电流,UCa、UCb、UCc为逆变器输出电压,L、R分别为逆变器交流侧的电感及其等效电阻,ICa、ICb、ICc为逆变器产生的补偿电流,Cdc1、Cdc2、Udc1、Udc2分别表示逆变器直流侧的上下电容值与电压值.

图1 三相四线制并联型 APF 系统主电路Fig.1 Main circuit of three-phase four-wire shunt APF
APF 主电路每相桥臂的上下开关管不能在同一时刻导通,在不考虑死区的情况下,上下开关管为互补状态.因此,主电路总共有 8 种开关模式,不同的开关模式对应不同的相电压.以直流侧电压Udc为单位长度,可以使空间矢量归一化.传统的 3D-SVPWM 算法是基于αβγ坐标系的,利用如式(1)所示的变换矩阵Tabc/αβγ可将相电压由abc坐标系转换到αβγ坐标系中,并由此得到如表 1 所示的空间矢量表,单位长度为Udc.
(1)
将αβγ坐标系下的8个空间矢量映射到αβγ坐标系上,如图 2 所示.可知 V0和V7两矢量在γ轴上,为γ轴上的正向和负向相量,直接参与矢量合成,对输出有影响.其他 6 个矢量在αβ平面上可划分为 6 个扇区,如图 3 所示,单位长度为Udc.

表1 空间矢量表Table 1 Switching vectors

图2 αβγ坐标系下的基本空间矢量分布Fig.2 Basic space vector distribution inαβγcoordinate

图3 αβ平面下的基本空间矢量分布Fig.3 Basic space vector distribution inαβplane
对于在任何一个扇区的空间矢量,均可根据积分相等原则由该扇区两边相邻的矢量合成.设欲合成的矢量的空间坐标为V,每个扇区的基本矢量由V0、V7以及扇区边界的两矢量VX、VY组成,则有
(2)
其中,Ts为开关周期.根据上式,以空间矢量V在扇区I为例,其基本矢量为V0、V7、V4、V6,将等式两边同除以开关周期Ts,并根据表 1 的空间矢量参数,可得如下矩阵形式:
(3)
式中,D0、D7、D4、D6为基本向量在一个开关周期内的占空比,DX=Tx/Ts.由式(3)进行变换可得
(4)
式中,Uα、Uβ、Uγ为αβγ坐标下的控制矢量.
此外,在扇区I的基本矢量为V0、V7、V4、V6,所对应三组开关上桥臂的开关状态分别为000、111、100、101.为了减小开关损耗,按照开关切换一次只变换一个开关状态的原则组织空间矢量切换的顺序,那么开关状态的转换应为000→100→101→111 →101→100→000.从而,可以得到当空间矢量V在扇区 I 时系统在abc坐标系中三相输出占空比为
(5)
将式(4)代入式(5),可得




(6)
式中,Ua、Ub、Uc为abc坐标系下三相空间矢量.同理,当空间矢量V位于其他扇区时,尽管空间矢量参数不同,但通过如式(3)-(6)的三相占空比与空间矢量的相应矩阵变换和推导,皆能得到与式(6)相同的表达式.
此外,由图 1 所示的 APF 主电路,根据基尔霍夫电压和电流定律,可得系统方程组如下:
(7)
式中,Sa、Sb、Sc分别为三相桥臂开关函数,且

(8)
式中,k代表a,b,c.由图1和式(7)可得变流器三相输出电压为
(9)
运用状态空间平均法,可将开关函数写为占空比的形式,即Sa=Da,则由式(9)可得系统在abc坐标系中三相输出占空比为
(10)
将上式转化为矩阵形式可得
(11)
对比式(11)和式(6),可见两个abc坐标下三相输出占空比的表达式是一致的.
由此可见,在应用 3D-SVPWM 调制算法计算三相输出占空比时,不论所合成的空间矢量位于哪一个扇区,最终得到的三相输出占空比都等于如式(6)所示的计算表达式.由此,传统调制算法中abc坐标到αβγ坐标变换、空间矢量所在扇区判断、扇区内基本矢量占空比等步骤是不必要并可以被省略的.文中所提出的优化的 3D-SVPWM 调制算法与传统 3D-SVPWM 算法的步骤对比如表2所示.采用文中所提出的优化 3D-SVPWM 调制算法,省去了传统调制算法中繁杂的abc坐标到αβγ坐标变换、合成的空间矢量所在扇区判断、扇区内基本矢量占空比计算等步骤,直接在abc坐标下采用三相电压控制量按式(6)所示的表达式计算三相的占空比,从而产生各桥臂开关管的通断信号,大幅简化调制算法,显著降低算法的复杂度和运算量,减少算法所占用系统软件资源,提高算法的实时性,为系统其他部分的控制算法提供了更多的空间和资源.

表2 两种调制算法步骤对比Table 2 Step comparison between two modulation methods
2仿真与实验验证
为了验证所提出算法的可行性和优越性,运用动态仿真软件 Matlab 建立的仿真模型进行了仿真分析.为了进一步验证算法,搭建了一台33 kW 的三相四线制电容中分式并联有源电力滤波器进行实验验证.系统仿真和实验参数如下:电源电压为220 V,频率为50 Hz,开关频率为9.6 kHz,直流侧上下电容为10 000 μF的电解电容,非线性负载为三相不控整流桥接纯电阻,R=15 Ω,直流电压参考值设为750 V.谐波检测方法采用瞬时无功功率法[21],直流侧电压外环和上下电容均压环均采用 PI 控制,电流内环控制采用基于 PI 和重复控制并联的复合控制策略[22].调制算法采用传统 3D-SVPWM 与文中所提出的优化 3D-SVPWM 算法进行对比实验.
图4和5分别为运用传统3D-SVPWM调制算法以及优化的 3D-SVPWM 调制算法得到的 APF 输出补偿电流和补偿后的电源电流仿真和实验波形.图中Is为电源电流,Ic为补偿电流,Iload为负载电流.由图可以看出,APF 输出的补偿电流很好地补偿了负载谐波.电源电流经补偿后接近正弦波.采用传统调制算法输出电流补偿后的电源电流总谐波畸变率(THD) 由补偿前的24.15%和24.88% 下降到补偿后的3.86%和4.65%,而采用优化算法输出电流补偿后的电源电流 THD 值则降为3.65%和4.55%.由此可见,采用两种调制算法系统的稳态补偿效果相当,改善了电源电流质量,达到国标标准,且采用优化调制算法的稳态性能略为优越.


图4 运用两种调制算法的电流仿真波形Fig.4 Simulated current waveforms obtained by two modulation algorithm


图5 运用两种调制算法的电流实验波形
Fig.5Experimental current waveforms obtained by two modulation algorithms
为了对比采用两种调制算法时系统的动态响应性能,给负载并联一个R=15 Ω的电阻使负载突变.在负载电流突然变大的情况下,将优化的调制算法与传统的调制算法进行比较.图6和7为当负载发生突变时分别采用两种调制算法的APF输出补偿电流和补偿后的电源电流的仿真和实验波形.由图可见,采用两种调制算法均能使系统输出迅速跟上负载变化,实时准确补偿突变的谐波电流,两种调制算法的动态响应性能相当.
此外,当系统三相负载不平衡时,分别采用两种调制算法,图 8 为补偿前后的三相电源电流实验波形.由图可见,补偿前三相电流有效值分别为34.7、44.6、36.8A,处于三相不平衡状态,经采用传统和优化调制算法的 APF 系统补偿后,负载谐波得到了很好的补偿,电源电流经补偿后接近正弦波,且有效值分别为43.6、45.1、44.1 A 及 44.1、45.8、44.8 A,很好地消除了三相不平衡现象.由此可得,采用两种调制算法,系统均能实现谐波消除并补偿三相不平衡的功能.
综上仿真和实验结果可知,在相同的系统参数、谐波检测方法、电压外环和电流内环控制器下,采用传统的调制算法和文中所提出的优化调制算法,系统均能快速准确的输出补偿电流,很好地补偿负载产生的谐波,APF 系统在稳态时皆能达到符合国标标准的补偿效果,且在负载突变时具有良好的动态性能.并且,当系统三相处在不平衡的情况下,仍能补偿三相不平衡状况,达到理想的谐波治理效果.然而,在达到同样系统性能的情况下,文中所提出的优化 3D-SVPWM 调制算法省去了传统调制算法中abc坐标到αβγ坐标变换、空间矢量所在扇区判断、扇区内基本矢量占空比计算等步骤,使调制算法得到极大简化,算法复杂度大为降低,计算量大幅减少,提高了算法的适用性和稳定性,有效的降低了系统的软硬件负荷,为其他控制算法在系统的优化和升级提供了更多的空间.


图6 负载突变时的电流仿真波形Fig.6 Simulated current waveforms when load suddenly changes


图7 负载突变时的电流实验波形Fig.7 Experimental current waveforms when load suddenly changes


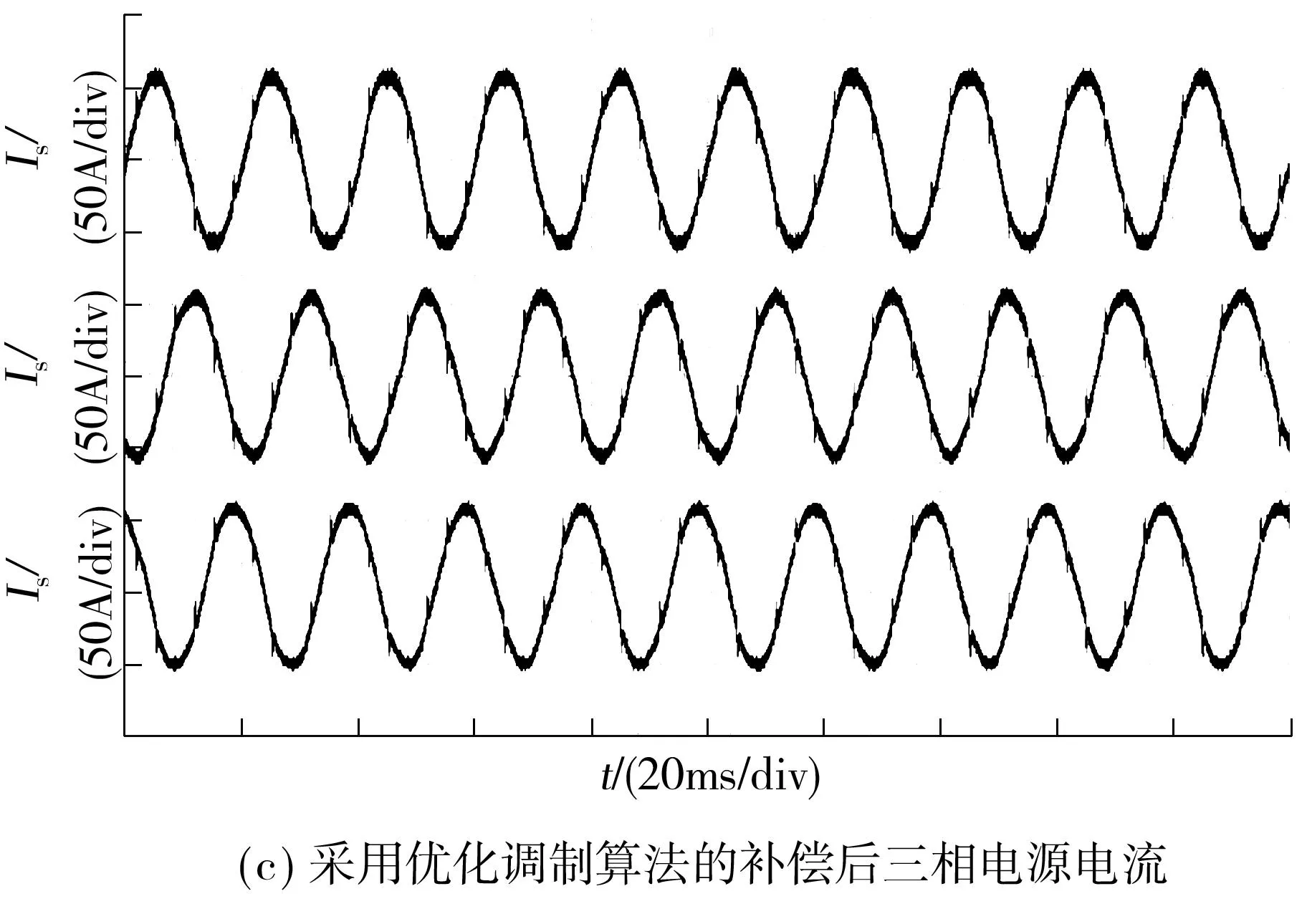
图8 三相负载不平衡情况下的电源电流Fig.8 Source currents in three-phase unbalance load situation
3结语
文中在深入分析和推导传统 3D-SVPWM 调制算法的基础上,证明传统算法在其运算的过程中是可以省略和简化的,并由此对 3D-SVPWM 算法进行优化.采用文中所提出的调制算法,可以在系统稳态、动态和负载不平衡等情况下保证良好的效果和性能,而且在此前提下极大地简化了传统的调制算法,改变传统算法过程复杂、计算量大的不足,增强调制算法的实时性和稳定性,减轻系统的软件负担,为系统其他部分的控制算法的设计和改良提供了更多的空间资源.在此基础上,可进一步探索在其他三相四线制电气设备上的应用和改进,具有理论和实际应用意义.
参考文献:
[1]Yao Wen-xi,Hu Hai-bing,Lu Zheng-yu.Comparisons of space-vector modulation and carrier-based modulation of multilevel inverter [J].IEEE Transaction on Power Electronics,2008,23(71):45-51.
[2]K Wei,Z Li-xia,W Yan-song.Study on output characteristic of bi-direction current source converters [J].IET Power Electronics,2012,5(7):929-934.
[3]周卫平,吴正国,唐劲松,等.SVPWM的等效算法及SVPWM与SPWM的本质联系 [J].中国电机工程学报,2006,26(2):133-137.
Zhou Wei-ping,Wu Zheng-guo,Tang Jin-song,et al.A novel algorithm of SVPWM and the study on the essential relationship between SVPWM and SPWM [J].Procee-dings of the CSEE,2006,26(2):133-137.
[4]陈娟,何英杰,王新宇,等.三电平空间矢量与载波调制策略统一理论的研究 [J].中国电机工程学报,2013,33(9):71-78.
Chen Juan,He Ying-jie,Wang Xin-yu,et al.Research of the unity theory between three-level space vector and carrier-based PWM modulation strategy [J].Proceedings of the CSEE,2013,33(9):71-78.
[5]谭国俊,刘战,叶宗彬,等.基于线电压坐标系的ANPC-5L逆变器SVPWM算法的研究 [J].中国电机工程学报,2013,33(30):26-33.
Tan Guo-jun,Liu Zhan,Ye Zong-bin,et al.SVPWM algorithm based on line voltage coordinate transformation for ANPC-5L inverter [J].Proceedings of the CSEE,2013,33(30):26-33.
[6]Bhat A H,Langer N.Capacitor voltage balancing of three-phase neutral-point-clamped rectifier using modified refe-rence vector [J].IEEE Transaction on Power Electronics,2014,29(2):561-568.
[7]Wang Wen,Luo An,Xu Xian-yong,et al.Space vector pulse-width modulation algorithm and DC-side voltage control strategy of three-phase four-switch active power filters [J].IET Power Electronics,2013,6(1):125-135.
[8]舒泽亮,丁娜,郭育华,等.基于SVPWM的STATCOM电压电流双环控制 [J].电力自动化设备,2008,28(9):27-30.
Shu Ze-liang,Ding Na,Guo Yu-hua,et al.SVPWM-based voltage-loop and current-loop controls of STATCOM [J].Electric Power Automation Equipment,2008,28(9):27-30.
[9]朱海锋,舒泽亮,高仕斌.二极管箝位五电平变换器的直流均压SVPWM快速算法 [J].电力自动化设备,2013,33(11):38-43.
Zhu Hai-feng.Shu Ze-liang,Gao Shi-bin.Fast SVPWM algorithm with DC voltage equalization for five level diode-clamped converter [J].Electric Power Automation Equipment,2013,33(11):38-43.
[10]Chen Keng-yuan,Hu Jwu-sheng.A filtered SVPWM for multiphase voltage source inverters considering finite pulse-width resolution [J].IEEE Transaction on Power Electronics,2012,27(7):3107-3118.
[11]Shu Ze-liang,Ding Na,Chen Jie,et al.Multilevel SVPWM with DC-link capacitor voltage balancing control for diode-clamped multilevel converter based STATCOM [J].IEEE Transaction on Industry Electronics,2013,60(5):1884-1896.
[13]许晓彦,杨才建,Janusz Mindykowski.有源滤波器空间矢量脉宽调制电流跟踪算法的优化 [J].电力系统自动化,2012,36(4):80-84.
Xu Xiao-yan,Yang Cai-jian,Janusz Mindykowski.Optimization on current tracking algorithm in active power filter based on SVPWM [J].Automation of Electric Power Systems,2012,36(4):80-84.
[14]Beig A R.Synchronized SVPWM algorithm for the over modulation region of a low switching frequency medium-voltage three-level VSI [J].IEEE Transaction on Industry Electronics,2012,59(12):4545-4554.
[15]周娟,吴璇,蒋正友,等.四桥臂变流器新型三维空间矢量脉宽调制策略 [J].中国电机工程学报,2011,31(33):1-8.
Zhou Juan,Wu Xuan,Jiang Zheng-you,et al.A novel 3D-SVPWM algorithm for four-leg converter [J].Proceedings of the CSEE,2011,31(33):1-8.
[16]Jose I Leon,Sergio Vazquez,Ramon Portillo,et al.Three-dimensional feed forward space vector modulation applied to multilevel diode-clamped converters [J].IEEE Tran-saction on Industry Electronics,2009,56(1):5101-5109.
[17]Li Xiang-sheng,Deng Zhi-quan,Chen Zhi-da,et al.Analysis and simplification of three-dimensional space vector PWM for three-phase four-leg inverters [J].IEEE Transaction on Industry Electronics,2011,58(2):450-464.
[18]Kouzou A,Mahmoudi M O,Boucherit M S.A new 3D-SVPWM algorithm for four-leg inverters [C]∥IEEE International Electric Machines and Drives Conference.California:IEEE,2009:1674-1681.
[19]乐江源,谢运祥,张志,等.有源电力滤波器状态反馈精确线性化控制 [J].电力自动化设备,2010,30(2):81-85.
Le Jiang-yuan,Xie Yun-xiang,Zhang Zhi,et al.State feedback exact linearization control for APF [J].Electric Power Automation Equipment,2010,30(2):81-85.
[20]王晓刚,谢运祥,帅定新,等.基于模型预测控制的三相四桥臂有源电力滤波器 [J].华南理工大学学报:自然科学版,2009,37(11):56-163.
Wang Xiao-gang,Xie Yun-xiang,Shuai Ding-xin,et al.Three-phase four-leg active power filter based on model predictive control [J].Journal of South China University of Technology:Natural Science Edition,2009,37(11):56-163.
[21]谢运祥,陈坤鹏,邓衍平,等.改进型谐波与基波有功和无功电流检测 [J].华南理工大学学报:自然科学版,2005,33(4):15-19.
Xie Yun-xiang,Chen Kun-peng,Deng Yan-ping,et al.Improved detecting method for harmonic and fundamental active and reactive currents [J].Journal of South China University of Technology:,2005,33(4):15-19.
[22]武健,何娜,徐殿国.重复控制在并联有源滤波器中的应用 [J].中国电机工程学报,2008,28(18):66-72.
Wu Jian,He Na,Xu Dian-guo.Application of repetitive control technique in shunt active power filter [J].Proceedings of the CSEE,2008,28(18):66-72.
Optimization Design of Three-Dimensional Space Vector Pulse-Width Modulation Strategy for Three-Phase Four-Wire System
WangYuLiuXiangXieYun-xiang
(School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China)
Abstract:In this paper, the traditional three-dimensional space vector pulse width modulation(3D-SVPWM)algorithm is deeply analyzed, and it is proved that the traditional algorithm can be simplified. Then, an optimized 3D-SVPWM algorithm is proposed. In comparison with the traditional algorithm, the optimized algorithm becomes extremely simplified and can guarantee the system performance. Moreover, it effectively reduces the complexity and the computation amount, and improves the instantaneity and the stability, which helps to alleviate the software load and thus provides more space for other control algorithms in the system. Finally, the feasibility and superiority of the proposed optimized algorithm are verified through the simulation and experiment in a three-phase four-wire center-spilt shunt active power filter.
Key words:three-dimensional space vector pulse width modulation;simplified algorithm; active filter
中图分类号:TM 461
doi:10.3969/j.issn.1000-565X.2015.08.004
文章编号:1000-565X(2015)08-0021-08
作者简介:王裕(1984-),男,博士生,主要从事有源电力滤波器研究.E-mail: xiaodou10@126.com
*基金项目:国家自然科学基金资助项目(51107044);广东省教育部产学研结合项目(2011B090400136)
收稿日期:2014-12-08
Foundation items: Supported by the National Natural Science Foundation of China(51107044)and the Project of Integration of Industry,Education and Research of Guangdong Province and Ministry of Education of China(2011B090400136)

