基于高阶内模的非线性离散系统迭代学习控制
周 伟,于 淼
(浙江大学 电气工程学院,浙江 杭州310027)
自Arimoto等[1-2]针对工业机械手系统可重复的特点,提出一种迭代学习算法以来,这种智能控制技术[3-4]引起了人们极大的兴趣.迭代学习控制将非线性系统作为研究对象,通过不断迭代而达到期望行为.在迭代学习控制的发展过程中涌现了许多热点问题,得到了诸多专家学者的关注,如经典迭代学习控制[5]、高阶迭代学习控制[6]、鲁棒迭代学习控制、最优迭代学习控制、自适应迭代学习控制[7]等.短短二十几年,迭代学习控制获得了极大的发展.
迭代学习控制本质上是通过对输出误差的不断修正,而实现自我学习的[8-9].利用前一次或前几次操作时测得的误差信息修正控制输入,控制器的综合结构简单,在线计算负担小[10].针对非线性系统,使用时变的学习控制技术可以改善控制性能[11].尤其当模型未完全已知,或不能充分展现被控对象的全部客观规律时,迭代学习控制可以充分利用被控对象可以重复运行的特点,不断更新控制输入,通过多次迭代后,实现对系统参考输出轨迹的零误差追踪[12].
传统的迭代学习控制在追踪参考轨迹的过程中,要求参考轨迹必须是迭代不变的.然而,实际上很难满足如此严格的重复性[13].比如,机械手在上一次工作过程中,在[0 ,T ]期间追踪某一参考轨迹,在下一次工作时,可能追踪另一相关的参考轨迹.根据内模原理可知,当受控对象追踪某一目标轨迹时,控制回路必须包含产生目标轨迹的动力系统模型的全部信息[14].Moore[15]首先引入ω 算子用来描述迭代域的变化情况.Liu等[16]针对连续系统参考轨迹的迭代域非严格重复性问题,通过将高阶内模和迭代学习控制方法相结合,利用λ范数,证明了基于高阶内模的迭代学习方法的有效性.Yin等[17]针对带不确定参数的非线性系统的迭代学习问题,使用高阶内模描述时变且沿迭代域变化的参数,设计基于高阶内模的参数学习律,并用Lyaponov方法证明了迭代域的渐近收敛.随着计算机控制技术的广泛应用,离散系统的控制问题受到越来越多的重视.尤其当系统中存在非线性因素时,无法将连续系统中已经得到的结论直接应用于离散系统.另外,迭代学习过程的实现总是离散的.针对离散系统,研究参考轨迹的迭代域非严格重复问题具有现实意义.
本文针对一类一阶非正则离散时间非线性系统参考轨迹的非严格重复性问题,提出基于内模原理的控制方法.针对由高阶内模产生的参考轨迹,使用一种D 型迭代学习控制律,从理论上证明了系统跟踪误差的收敛性.对于机械手模型的仿真结果证明了所提出方法的有效性.
1 问题描述
系统方程如下式所示:

式中:下标k表示迭代次数;t∈[0 ,T ],[0 ,T ]表示离散时间{0,1,…,T };xk(t)∈Rn;uk(t)和yk(t)分别为第k 次迭代时的输入和输出向量,uk(t)∈Rm,yk(t)∈Rm;f (xk(t))∈Rn;B(t)∈Rn×m、C(t)∈Rm×n均为关于t的有界函数.系统(1)为离散一阶非正则系统,在有限时间区间[0 ,T ]上重复运行.
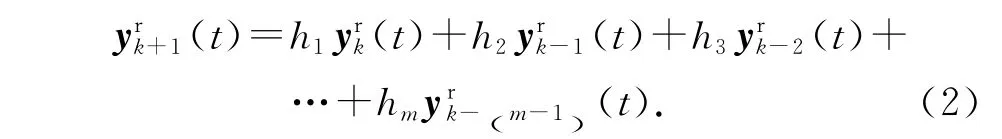
式中:hi(i=1,2,…,m)为稳定的多项式 H (z) =zm-h1zm-1-h2zm-2-…-hm的系数.式(2)描述了参考轨迹迭代域变化的规律性.由式(2)可以看出,参考轨迹迭代相关,且变化规律是已知的.另外,根据m 阶内模求得参考轨迹(t),需要m 个初始轨迹(t),(t),…,(t).记 多 项 式 算 子H (ω-1)为

将式(2)改写为

系统(1)满足如下假设.
假设1 非线性函数f (xk(t))在有限时间区间[0 ,T ]上关 于xk满 足 一 致 全局Lipschitz条 件,即满足:‖f (x1)-f (x2)‖≤lf‖x1-x2‖,其中lf为Lipschitz系数.
假设2 系统初值条件满足:ek(0) =0,k=1,2,….
假设3 m 阶内模生成的参考轨迹满足:多项式 H (z) =zm-h1zm-1-h2zm-2-…-hm是 稳 定的,即多项式的特征方程的所有根位于单位圆内部,或在单位圆上仅有单根或共轭复根.
系统输出追踪由m 阶内模生成的参考轨迹,首先,随着迭代次数的增加,参考轨迹不能趋于发散.因此,上述多项式构成的特征方程的根必须位于单位圆内部,或仅有单根或共轭复根落在单位圆上.其次,若上述多项式构成的特征方程的根全部位于单位圆的内部,上述多项式是稳定的,并且当迭代次数趋向无穷时,由m 阶内模生成的参考轨迹最终会收敛到零.因为这种情况下,由m 阶内模产生的参考轨迹的变化趋势是渐近稳定的.最后,若特征方程至少在单位圆上有单根或共轭复根,则由m 阶内模生成的参考轨迹在迭代域上会不断变化,且不会收敛到零.
例如,当H1(ω-1)=1 时,有(t)=(t),追踪的参考轨迹迭代域不变,属于高阶内模生成的参考轨迹的特殊情况.当H2(ω-1)=ω-1时,高阶内模生成的参考轨迹满足的多项式为H2(z) =z2-1,特征根为z1,2=±1,都位于单位圆上.此时,(t)=(t).基于迭代域的算子ω 的定义来源于z 变换的概念,因此仿照z 变换的方法求解(t)可得,y(t)=D1(t)·1k+D2(t)·(- 1 )k.其中,D1(t)及D2(t)为与迭代无关的待定时变系数,由初始条件决定.这意味着在奇数次迭代时,追踪的参考轨迹都相同,即(t)=D1(t)-D2(t)=…=(t);在偶数次迭代时,追踪的参考轨迹相同,即(t)=D1(t)+D2(t)=…=(t),k=1,2,…,N.由此可见,由高阶内模H2(ω-1)生成的参考轨迹在迭代域上,以2次迭代为周期,参考轨迹会发生重复性变化,但是不会收敛到零.

定义1 函数f(t)的λ范数[21]为
定义2 表征m 阶内模的多项式算子H (ω-1)和输出追踪误差乘积的λ范数为
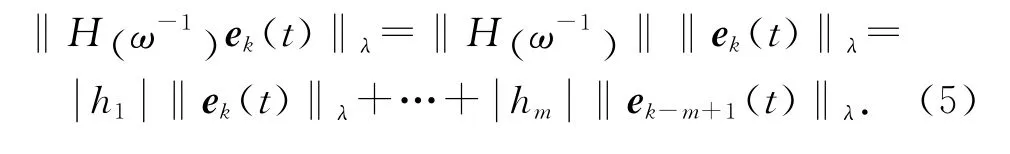
2 迭代学习控制律的设计
控制目标是设计迭代学习控制律uk+1(t),使得当k→∞时,

针对基于高阶内模的参考轨迹,采用含有m 阶内模的D 型迭代学习控制律:

即

其中H (ω-1)的定义如式(3)所示,学习增益γk的定义为

定理:对于满足假设1、2、3和4的一阶非正则离散时间非线性系统(1),针对参考轨迹(2),采用含有m 阶内模的D 型迭代学习控制律(6),选择学习增益γk,使得下列特征多项式渐近稳定:

式中:ζt,j=‖hk+1-jIm-C(t)B (t- 1)γk+1-j‖,Im∈Rm×m为单位矩阵,t∈[1 ,T+1] ,j∈[k,k-1,…,km+1],系统跟踪误差沿迭代方向收敛到0,即

3 收敛性证明
定义第k+1次迭代时的输出追踪误差为

将满足m 阶内模的输出跟踪轨迹(4)代入可得

将式(1)代入式(9),可得

整理可得

由式(3)、(4)可知,
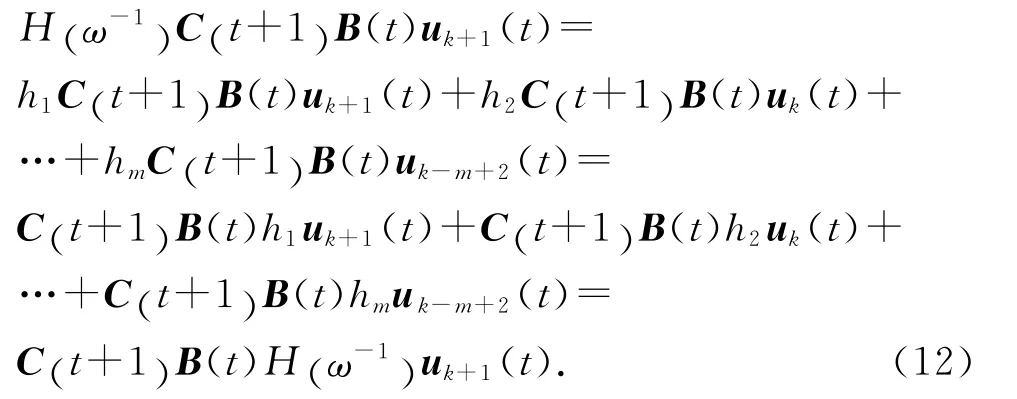
对式(11)两端取范数,并将式(7)代入可得
在式(13)中,令

并整理可得

考虑到函数f(t)满足假设1,式(14)可变为
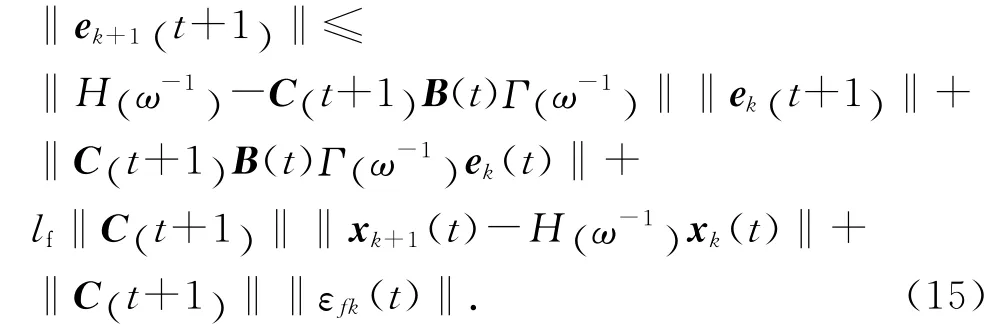
由式(1)可得

根据式(13),对式(16)两端取范数可得
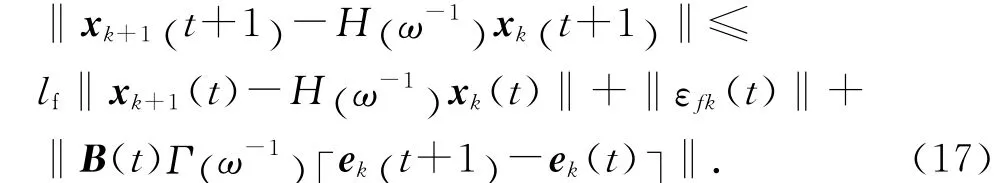
然后将式(17)在t∈[0 ,T ]展开.当t=0时,有
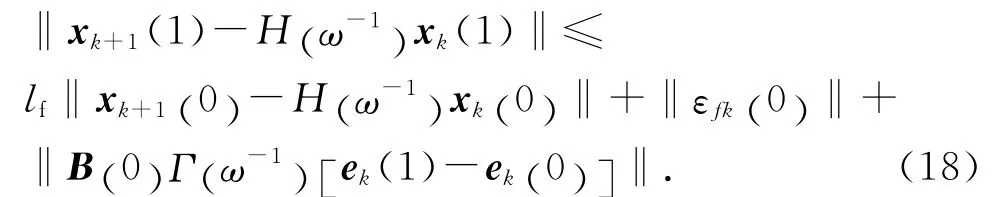
根据假设2可知,
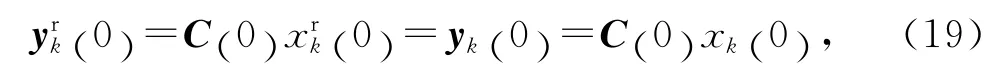

可得:xk+1(0) =H (ω-1)xk(0) .将其代入式(18),有
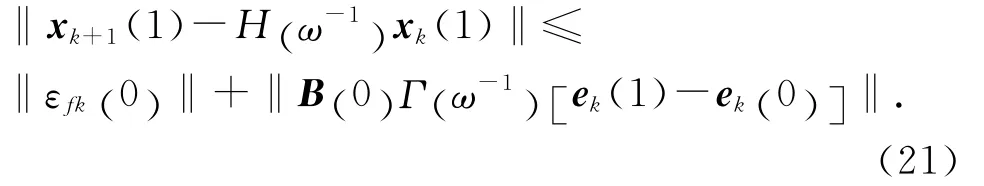
同理有

依此类推,可得
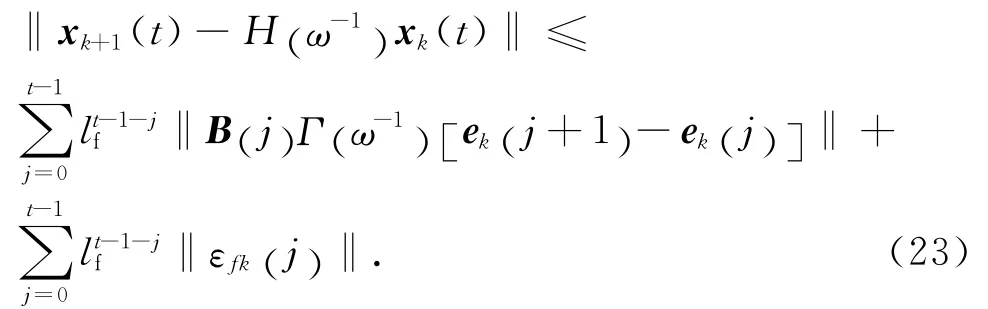
将式(23)代入式(15),有

将式(24)两端同时乘以exp(-λ(t +1) ),然后在区间[0 ,T ]上取上界;根据假设4,可得

在式(25)中,可得

式中:

同理可得
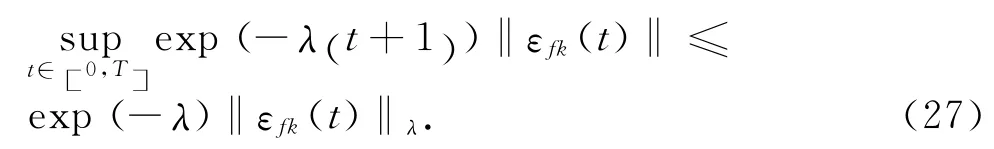
另外,可得
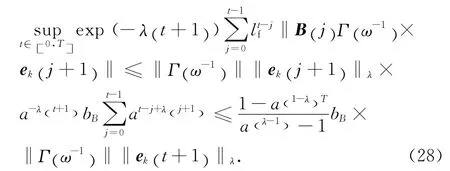
同理有,

将式(26)~(29)代入式(25)可知,

式中:
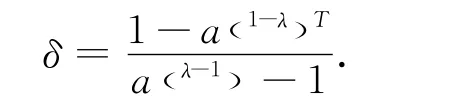
将式(30)各项中的高阶内模完整表示出来,则有

将式(31)~(33)代入式(30),再将式(30)由t=0到t=T逐项写出,并记αt+1=a-λbC[δ+ 1] ‖εfk(t)‖λ,t∈[0 ,T] ,可知,当t=0时,有
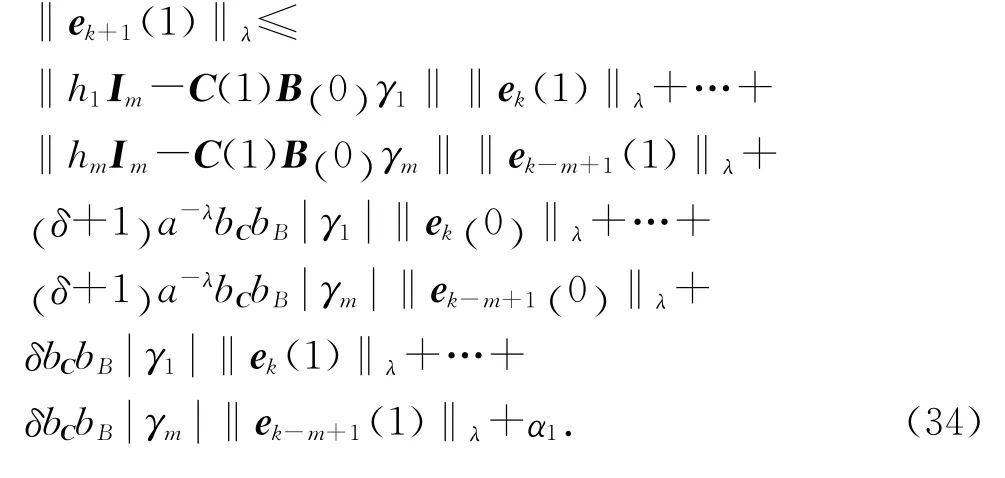
同理,逐步推知,当t=T 时,有

注意到假设2,对不等式(35)进行整理,并令
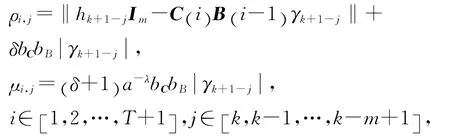
可知,当t∈[0 ,T] 时,有

当t=0时,满足

将t=0到t=T 的每一项展开并写成矩阵形式如下:
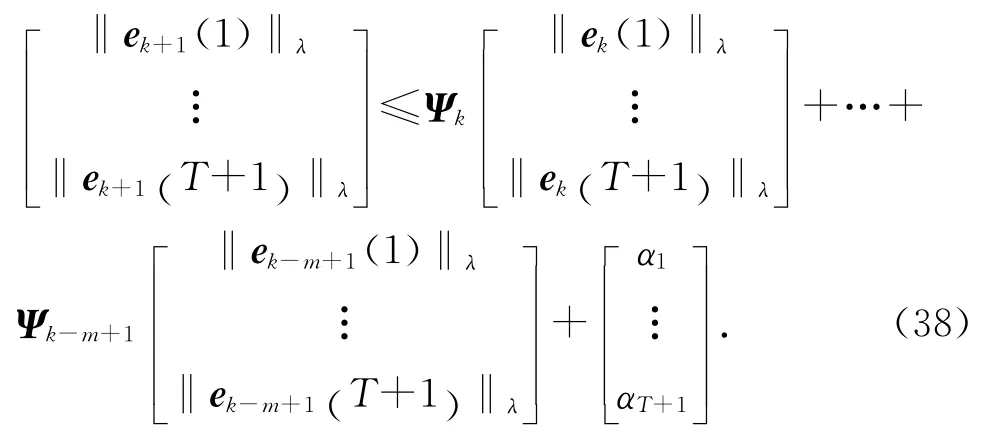
式中:

当k=0时,有
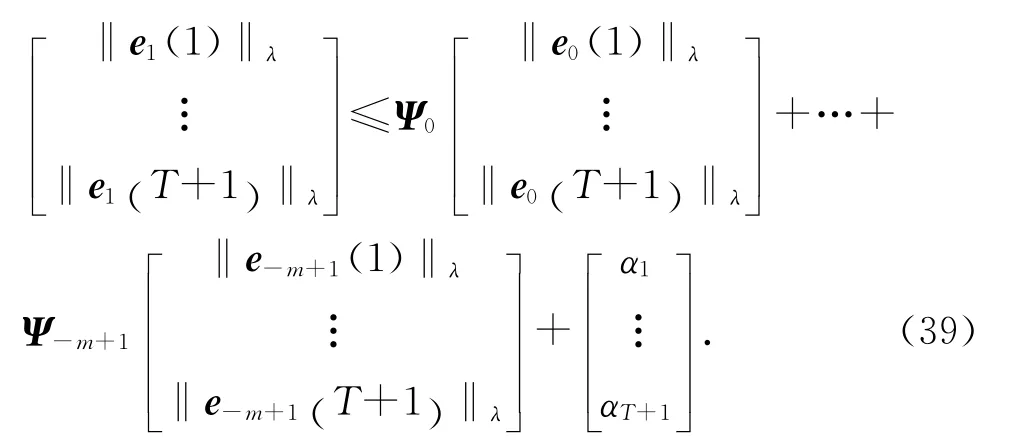
式中:Ψs(s∈[1-m,2-m,…,0] ),满足

首先分析不等式(36)中的μt+1,j和ρt+1,j.可以看出,当λ取足够大时,μt+1,j以及ρt+1,j中的δ可以达到任意小.其次,分析αt+1,t∈[0 ,T ].可以看出,αt+1中的‖εfk(t)‖λ是关于λ的函数.由于
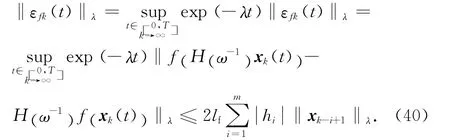


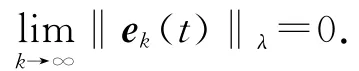
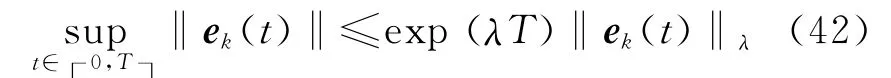
4 仿真结果
考虑单连杆机械手的轨迹跟踪问题.单连杆机械手模型的系统方程[22-24]为


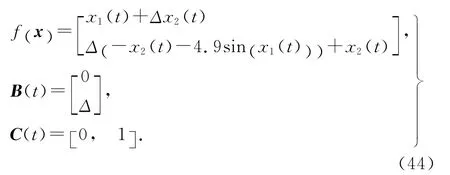
由于C( t+ 1 )B(t)=[0 ,1] [0,Δ]T≠0,可知系统为一阶非正则.
追踪的参考轨迹为

其中第一次及第二次迭代的追踪轨迹如下:

输出追踪参考轨迹中内含的二阶内模系数为:h1=2cos (10 Δ) ,h2=-1,因此,控制取为

选 择 学 习 增 益γ1=1.59/Δ,γ2=-1.10/Δ.(ek(t+ 1) -ek(t))/Δ 是机械手系统(43)在 第k 次迭代时的输出追踪误差的一阶导数[25],即控制输入(47)可以看成是连续系统(43)的下述学习控制律的离散化:
收敛条件为:‖h1I-γ1CB‖=0.4<1,‖h2Iγ2CB‖=0.1<1.对应的特征多项式为:z2-0.4z-0.1.它的2个特征根分别为z1=0.57,z2=-0.17,都位于单位圆内.
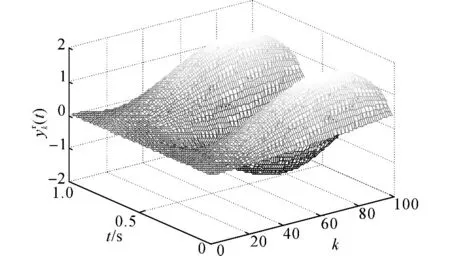
图1 迭代变化的追踪参考轨迹Fig.1 Iteration-varying reference trajectory
图1给出参考轨迹在时域和迭代域下的变化情况.由式(45)可知,迭代变化的参考轨迹满足,多项式 H (z) =z2-2cos (10 Δ) z+1的特征根是一对位于单位圆上的共轭复根.仿照z 变换的方式求解式(45)可得,(t)=Da(t)·cos (10 Δk) +Db(t)×sin (10 Δk) ,其中Da(t)及Db(t)为与迭代无关的待定时变系数,由初始条件决定.由此可知,参考轨迹(45)在迭代域上会不断变化,不会重复,且不会收敛到零.从图1可以看出,满足m 阶内模的参考轨迹(45)在迭代域内不断振荡,完全不重复.定义第k次迭代的输出均方根误差为

表1给出不同的迭代次数时,系统的输出均方根误差.图2给出系统沿迭代方向的输出均方根误差.图3展示了第3次、第7次及第10次迭代时系统的输出追踪情况.从图2、3可以看出,随着迭代次数的增加,系统输出逐渐收敛到参考轨迹.第10次迭代时,系统输出已经能够很好地追踪参考轨迹.另外,第3次迭代时追踪的参考轨迹和第10次迭代时追踪的参考轨迹完全不同,采用基于高阶内模的D型迭代算法能够很好地实现追踪.当选择输出均方根误差的许可范围为小于0.01 时,从表1 可以看出,第8次迭代之后,系统的输出均方根误差都在许可范围之内.
为了与本文含有m 阶内模的D 型迭代学习控制律(47)相比较,给出含有m 阶内模的P 型[26]迭代学习控制律的仿真结果.控制输入如下式所示:

表1 基于高阶内模的D型迭代学习律的输出均方根误差Tab.1 Output tracking root-mean-square error of HOIMbased D-type ILC

图2 采用基于高阶内模的D型迭代学习律的系统沿迭代方向的输出均方根误差Fig.2 Output tracking root-mean-square error of HOIM-based D-type ILC along iteration axis
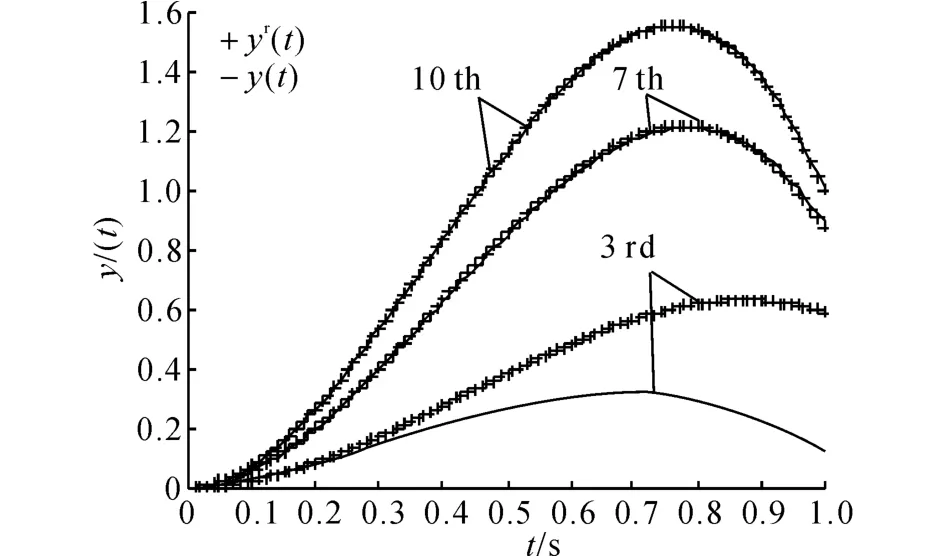
图3 第3、7及10次迭代时的追踪Fig.3 Tracking profiles of HOIM-based ILC for 3rd,7th and 10th iterations
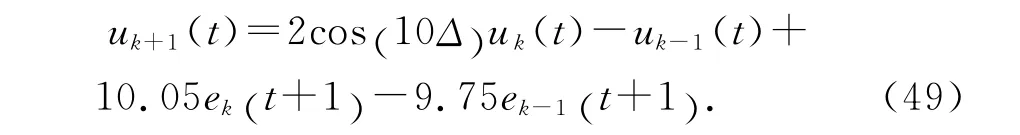
表2给出不同迭代次数时系统的输出均方根误差.系统沿迭代方向的输出均方根误差曲线如图4所示.
考虑到含有高阶内模的迭代学习控制律形式与传统的高阶迭代学习控制律形式相似,为了与采用高阶内模的迭代学习控制对比,给出采用高阶迭代学习律时的系统追踪情况.选取控制输入如下式所示:

表2 基于高阶内模的P型迭代学习律的输出均方根误差Tab.2 Output tracking root-mean-square error of HOIMbased P-type ILC

图4 采用基于高阶内模的P型迭代学习律的系统沿迭代方向的输出均方根误差Fig.4 Output tracking root-mean-square error of HOIM-based P-type ILC along iteration axis

选择P1=1.91,P2=-0.91,Q1=2.65,Q2=-1.图5给出采用高阶迭代学习算法,迭代100次时,系统的输出均方根误差曲线.表3给出不同的迭代次数时,系统的输出均方根误差.将图4、5与图2对比可见,采用基于高阶内模的D 型迭代学习方法,与采用另外2种迭代学习控制方法相比,在收敛过程中的振荡较少,收敛过程更加平稳,收敛速度显著加快.
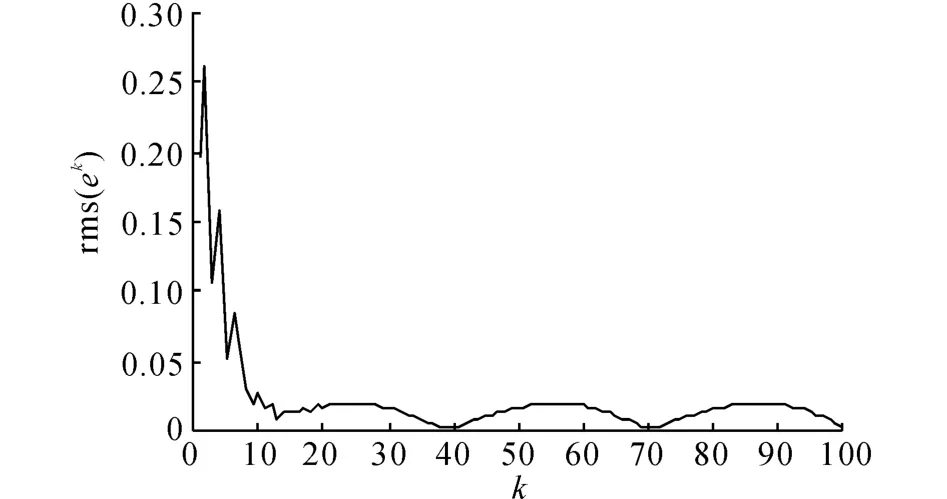
图5 采用高阶迭代学习算法时沿迭代方向的输出均方根误差Fig.5 Output tracking root-mean-square error with high order ILC algorithm along iteration axis

表3 基于高阶迭代学习算法的输出均方根误差Tab.3 Output tracking root-mean-square error of high order ILC
5 结 论
(1)本文针对由高阶内模产生的参考轨迹,设计基于高阶内模的迭代学习控制,系统跟踪误差可以在有限时间内收敛到零.
(2)通过对机械手模型的离散化,然后设计学习增益,并进行仿真分析.可以发现,采用基于高阶内模的D 型迭代学习控制方法能够很好地追踪迭代域变化的参考轨迹,经过较少的迭代次数能够达到系统追踪的要求.
(3)针对追踪轨迹迭代域的非严格重复问题,高阶迭代学习具有一定的鲁棒性,但不能达到渐近收敛.
(
):
[1]ARIMOTO S,KAWAMURA S,MIYAZAKI F.Bettering operation of robots by learning[J].Journal of Robotic Systems,1984,1(2):123-140.
[2]ARIMOTO S,KAWAMURA S,MIYAZAKI F.Bettering operation of dynamic systems by learning:a new control theory for servomechanism or mechatronics systems[C]∥Proceedings of 23rd Conference on Decision and Control.Las Vegas:IEEE,1984:1064-1069.
[3]张兴国,林辉.迭代学习控制理论进展与展望[J].测控技术,2006,25(11):1-5.ZHANG Xing-guo,LIN Hui.Recent developments and prospects of iterative learning control theory[J].Measurement and Control Technology,2006,25(11):1-5.
[4]许建新,侯忠生.学习控制的现状与展望[J].自动化学报,2005,31(6):943-955.XU Jian-xin,HOU Zhong-sheng.On learning control:the state of the art and perspective[J].ACTA Automatica Sinica,2005,31(6):943-955.
[5]ARIMOTO S.Learning control theory for robotic motion[J].International Journal of Adaptive Control and Signal Processing,1990,4(6):543-564.
[6]CHEN Yang-quan,WEN Chang-yun,SUN Ming-xuan.A robust high-order P-type iterative controller using current iteration tracking error[J].International Journal of Control,1997,68(2):331-342.
[7]FRENCH M,ROGERS E.Non-linear iterative learning by an adaptive Lyapunov technique[J].International Journal of Control,2000,73(10):840-850.
[8]王晔,刘山.期望轨迹可变的非线性时变系统迭代学习控制 [J].浙 江 大 学 学 报:工 学 版,2009,43(5):839-843.WANG Ye,LIU Shan.Iterative learning control of nonidentical desired trajectories for a class of nonlinear timevarying systems[J].Journal of Zhejiang University:Engineering Science,2009,43(5):839-843.
[9]于淼,王佳森,齐冬莲.具有未知控制方向的输出反馈自适应学习控制[J].浙江大学学报:工学版,2013,47(8):1424-1430.YU Miao,WANG Jia-sen,QI Dong-lian.Output-feedback adaptive learning control with unknown control direction[J].Journal of Zhejiang University:Engineering Science,2013,47(8):1424-1430.
[10]孙明轩,黄宝健.迭代学习控制[M].北京:国防工业出版社,2000:2-3.
[11]BONDI P,CASALINO G,GAMBARDELLA L.On the iterative learning control theory for robotic manipulators[J].IEEE Journal of Robotics and Automation,1988,4(1):14-22.
[12]马航,杨俊友,袁琳.迭代学习控制研究现状与趋势[J].控制工程,2009,16(3):286-290.MA Hang,YANG Jun-you,YUAN Lin.Current state and trend of iterative learning control[J].Control Engineering of China,2009,16(3):286-290.
[13]XU Jian-xin.Direct learning of control efforts for trajectories with different magnitude scales[J].Automatica,1997,33(12):2191-2195.
[14]TAYEBI A,ZAREMBA M B.Internal model-based robust iterative learning control for uncertain LTI systems[C]∥Proceedings of the 39th IEEE Conference on Decision and Control.Sydney:IEEE,2000:3439-3444.
[15]MOORE K L.A matrix fraction approach to higher-order iterative learning control:2-D dynamics through repetition-domain filtering [C]∥Proceedings of the Second International Workshop on Multidimensional(ND)Systems.Czocha Castle:[s.n.],2000:99-104.
[16]LIU Chun-ping,XU Jian-xin,WU Jun.On iterative learning control with high-order internal models[J].International Journal of Adaptive Control and Signal Processing,2010,24(9):731-742.
[17]YIN Chen-kun,XU Jian-xin,HOU Zhong-sheng.A high-order internal model based iterative learning control scheme for nonlinear systems with time-iterationvarying parameters[J].IEEE Transactions on Automatic Control,2010,55(11):2665-2670.
[18]CHI Rong-hu,HOU Zhong-sheng,XU Jian-xin.Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition[J].Automatica,2008,44(8):2207-2213.
[19]LIU Chun-ping,XU Jian-xin,WU Jun.Iterative learning control with high-order internal model for linear time-varying systems[C]∥Proceedings of 2009 American Control Conference.St.Louis:IEEE,2009:1634-1639.
[20]CHEN Yang-quan,MOORE K L.Harnessing the nonrepetitiveness in iterative learning control[C]∥Proceedings of the 41st IEEE Conference on Decision and Control.Las Vegas:IEEE,2002:3350-3355.
[21]CHIEN C J.A discrete iterative learning control for a class of nonlinear time-varying systems [J].IEEE Transactions on Automatic Control,1998,43(5):748-752.
[22]SUN Ming-xuan,WANG Dan-wei.Initial shift issues on discrete-time iterative learning control with system relative degree[J].IEEE Transactions on Automatic Control,2003,48(1):144-148.
[23]WANG Dan-wei.Convergence and robustness of discrete time nonlinear systems with iterative learning control[J].Automatica,1998,34(11):1445-1448.
[24]HWANG D H,BIEN Z,OH S R.Iterative learning control method for discrete-time dynamic systems[J].IEE Proceedings-D:Control Theory and Applications,1991,138(2):139-144.
[25]JANG T J,AHN H S,CHOI C H.Iterative learning control for discrete-time nonlinear systems[J].International Journal of Systems Science,1994,25(7):1179-1189.
[26]MOORE K L.An observation about monotonic convergence in discrete-time,P-type iterative learning control[C]∥Proceedings of the 2001IEEE International Symposium on Intelligent Control.Mexico:IEEE,2001:45-49.

