基于希尔伯特变换的自传感电磁轴承实现

于 洁，祝长生

（浙江大学 电气工程学院，浙江 杭州310027）

主动电磁轴承因其无摩擦、无需润滑、低损耗等优良特性，在高速旋转机械上有着广阔的应用前景.一般的主动电磁轴承系统以转子的位移信号作为闭环控制的反馈量，因此需要在各自由度方向安装至少一个位移传感器.高精度的位移传感器价格昂贵，使得电磁轴承系统的成本大幅提高，可靠性降低，不利于电磁轴承技术在工业中的应用.此外，位移传感器探头中心与电磁轴承中心不在同一位置，增加了控制系统的难度，这在电磁轴承-柔性转子系统中尤为明显［1-2］.

针对上述问题，Vischer等［3］首先提出自传感电磁轴承的概念，有效地降低了电磁轴承系统的成本和安装复杂度，提高了可靠性.自传感电磁轴承系统已有多种实现方法，如状态观测器法［4］、差动变压器法［5］、解调法［6-10］、电流斜率检测法［11-12］等.其中基于解调法的自传感电磁轴承因其不需要对电磁轴承的本体结构进行改动，鲁棒性良好，硬件复杂度适中，近年来受到广泛的研究.Noh等［13］使用参数估计法补偿动态占空比变化对解调器输出的影响，实现了单自由度电磁轴承的无传感器运行.唐明等［14-15］分析力扰动下开关功放电流纹波频谱的分布规律.

在开关功放驱动的自传感电磁轴承系统中，可以利用功率器件通断引起的电流纹波实现对转子位置的估计.这通常由带通滤波、整流（绝对值）及低通滤波环节构成的前置解调模拟电路完成.在数字化实现整流滤波法时，非线性的整流（绝对值）环节将负值信号反转后会造成信号带宽的成倍增加，增加了低通滤波环节的设计难度.若继续采用模拟低通滤波器，则难以实现解调器精度和集成度的提高.

针对“整流滤波法”存在的问题，本文提出一种基于希尔伯特变换的位移估计策略.此外，针对自传感电磁轴承系统中多路信号实时处理的同步问题，本文给出一种FPGA＋DSP 的自传感电磁轴承数字化实现方案.通过FPGA 实现线圈电流信号的解调，而DSP实现开关功放实时占空比的检测和位置反馈控制算法.最后在4自由度径向电磁轴承-刚性转子系统平台上进行无传感器运行实验.

1 径向电磁轴承的电感模型和位移估计基本原理

1.1 径向电磁轴承的电感模型

常见的8磁极定子径向电磁轴承的结构如图1所示.在不考虑极间磁的耦合影响以及磁饱和影响时，可以将8磁极径向电磁轴承简化为如图2所示的单自由度模型［10］.

根据磁路理论，由安培环路定律、磁阻定义式可得

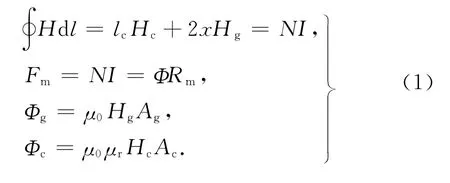
图1 八磁极定子结构径向电磁轴承Fig.1 Eight-pole stator structure of radial AMB

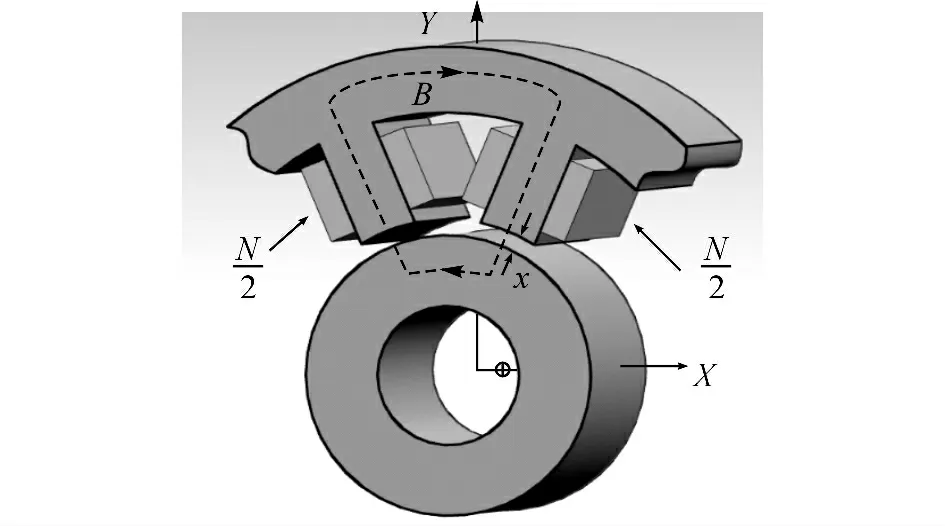
图2 单自由度电磁轴承模型Fig.2 Single-DOF model of AMB

式中：Hc及Hg分别为铁磁材料和气隙中的平均磁场强度，lc为铁磁材料中磁路的平均长度，x 为气隙长 度，N 为 线 圈 匝 数，I 为 线 圈 电 流，Φc为 定、转 子铁磁材料中的磁通量，Φg为气隙磁通，Ag及Ac分别为磁极、气隙截面积.

当忽略漏磁和边缘效应时，

联立式（1）、（2），可得磁阻Rm的表达式：

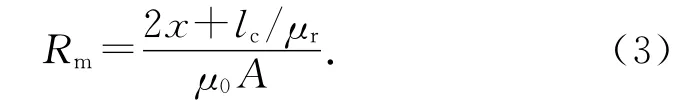
考虑到lc／μ≪2x，式（3）可以简化为

由电感和磁阻的关系，可得

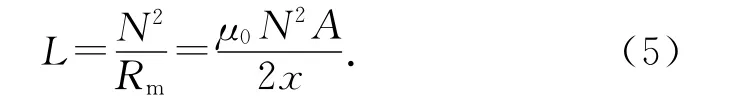
式中：L 为线圈电感.L 与x 成反比关系，其余为常数，故已知当前定子磁极的线圈电感，能够求得气隙的大小，即为自传感磁轴承实现位移估计的基本原理.

1.2 电流型开关功率放大器驱动下的位移估计原理

电流型开关功放的输出跟随参考输入Uref的输出电流和功率器件开关引起的高频电流纹波2部分组成.在有位移传感器的电磁轴承系统中，后者常被视为噪声.在无传感器电磁轴承系统中，高频电流纹波的幅值与线圈电感密切相关，故转子位置变动引起的线圈电感变化会反映在纹波幅值的变化中.为了获得这种关系，以图3所示的两电平恒频率电流型半桥开关功率放大器为例进行分析.

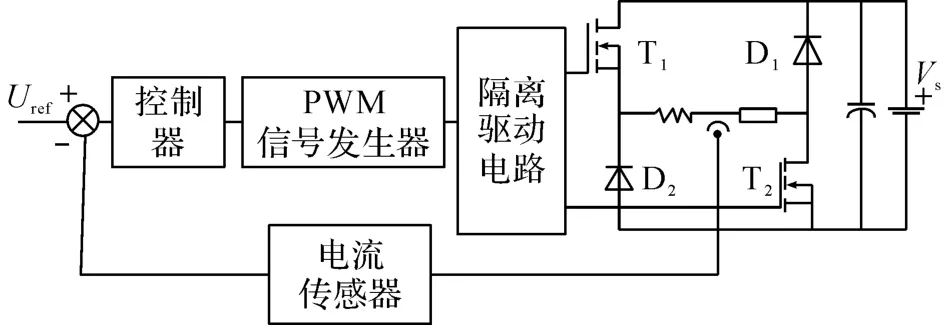
图3 两电平电流型开关功率放大器基本拓扑Fig.3 Double-state current type switching power amplifier

如图3所示的两电平恒频率电流型半桥开关功率放大器主要由半桥电路、隔离驱动电路、PWM 信号发生器、电流传感器及控制器等组成.

当PWM 信号为高电平时，开关管T1及T2导通，加在负载两端的电压为直流母线电压Vs，线圈电流上升；反之，二极管D1及D2导通，负载两端的电压为-Vs，线圈电流下降.

对图4所示线圈电压的理想波形进行建模.设PWM 信号的频率为fs，则第k 个周期内电磁轴承线圈电压V（t）为

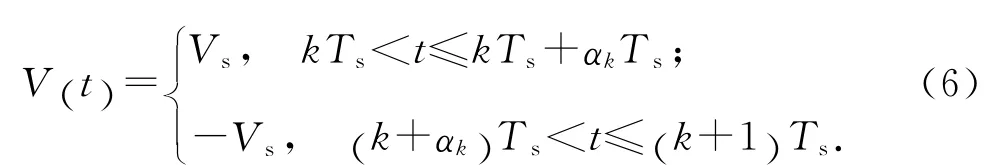
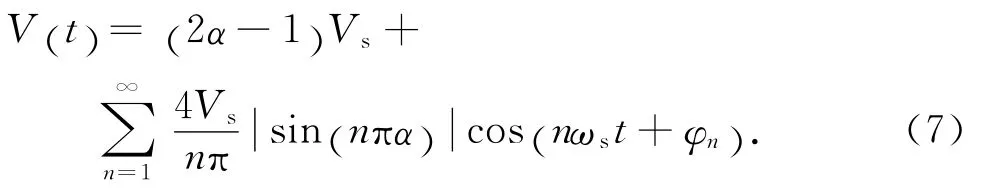
式中：Vs为直流母线电压.

对（6）作傅里叶分解，可得

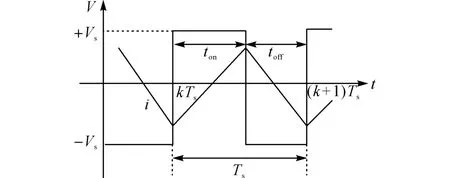
图4 开关功放驱动下的线圈电压、电流理想波形Fig.4 Ideal coil voltage and current waveforms when driven by switching power amplifier

式中：第一项与参考输入有关，第二项与开关纹波有关；n＝1，2，3… 分别对应开关纹波的基波（f＝fs）和高次谐波；α为占空比，α＝ton／Ts；φn 为相角，φn＝-nπα；ωs为开关角频率，ωs＝2πfs.

式（7）可以看作将开关功放加在线圈两端的电压信号分解成一系列电压源的线性加权.根据线性电路的叠加原理可知，线圈电流可以看作为上述电压源驱动下各电流分量的线性加权.考虑到高频激励下，线圈的感抗j nωsL 远大于线圈电阻R，因此可以忽略R 的影响，将其视为纯感性负载.开关电流纹波各阶次分量为

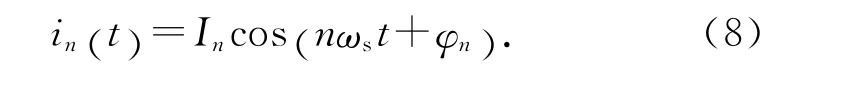
式中：

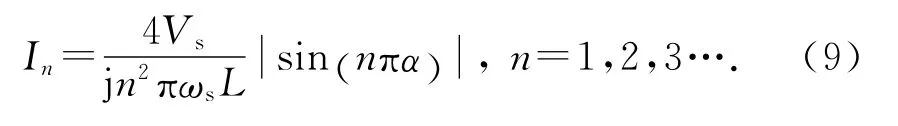
由于各阶分量的幅值与阶次的平方成反比，n＞1的高次谐波分量幅值随阶次的增加迅速减弱.从获得最高信噪比的角度出发，选用基波分量幅值I1用于位移估计.式（9）中取n＝1，并将式（5）代入，可得

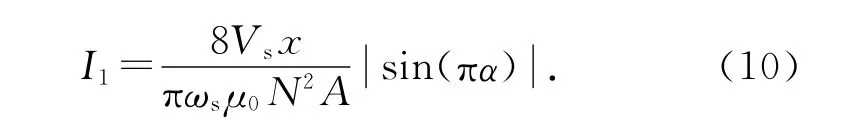
整理可得

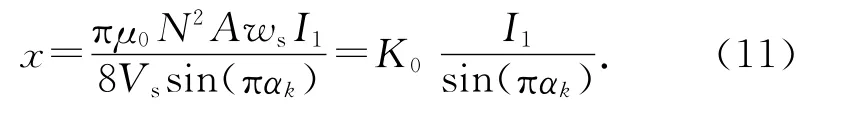
式中：K0＝π2μ0N2Afs／（4Vs）为常数.

由式（11）可知，若能够提取出基频纹波分量的幅值I1和PWM 波当前占空比α，则可以得到当前转子的实时气隙x.从信号处理的角度，可将电流纹波的基频分量i1（t）视为幅值随转子位置变化的调幅余弦信号.从电流信号中提取I1等价于求i1（t）的幅值包络信号.考虑到实际线圈电流中的频谱成分复杂［15］，电流信号须经过带通滤波环节以衰减基频分量外的其他分量.

如图5所示为从线圈电流i1（t）中提取I1的基本原理.

图5 提取基频分量幅值的基本原理Fig.5 Basic principle of demodulation of amplitude of fundamental component

2 基于希尔伯特变换的位移解调算法

2.1 线圈电流信号的频域特性和带通滤波器设计

根据1.2节的分析可知，两电平电流型开关功放驱动下的磁轴承线圈电流包括：①偏置直流分量；②控制器产生的与转子转速或振动频率相关的低频控制分量；③功率器件通断产生的与开关频率相关的纹波分量及谐波；④其他如直流电压源电压波动、非线性因素（如涡流）、电磁干扰等引起的噪声.

在无传感器磁轴承系统中，偏置直流分量及与转子转速或振动频率相关的低频控制分量分别产生电磁轴承的静态悬浮力和动态控制力，实现转子的稳定悬浮；功率器件通断产生的与开关频率相关的纹波分量及其高阶谐波理论上都可以用于转子实时位置的估计，但从提高信噪比的角度来说，一般选择具有最大幅值的开关纹波基频分量i1.需要注意的是，线圈电流信号中大多数的能量集中于偏置直流分量及与转子转速或振动频率相关的低频控制分量，如图6所示，因此从信号频域带宽的角度来说，线圈电流信号属于低频信号.

实际上，低频控制分量的频域范围受限于转速，一般小于2kHz；功率器件通断产生的与开关频率相关的纹波分量及其谐波的频域范围由功率器件开关频率fs决定，通常大于10kHz.两者在频域上不存在重叠，故i1的提取可以通过带通滤波实现，其中通带的中心频率位于fs，Noh等［13，16］使用模拟电路构建带通滤波器，唐明［17］使用4个2阶有源带通滤波器的级联构成8 阶带通滤波器来提高通带增益.为了避免使用模拟电路带来的诸多问题，采用数字带通滤波器.设计得到的IIR 带通滤波器的频域特性如图7所示.图7中，Mag、φ 和Q 分别为幅值、相位和群延迟.其中采样频率为200kHz，通带为［17kHz，25kHz］，过渡带宽为5kHz，滤波器阶数为28.

如图7 所示，IIR 滤波器不具有严格的线性相位特性（群延迟特性不为常数），但由于输出基本不包含i1外的其他频率成分，不存在波形失真问题.经过带通滤波，线圈电流中除i1外的分量均得到有效衰减，并输出给后续幅值提取环节.

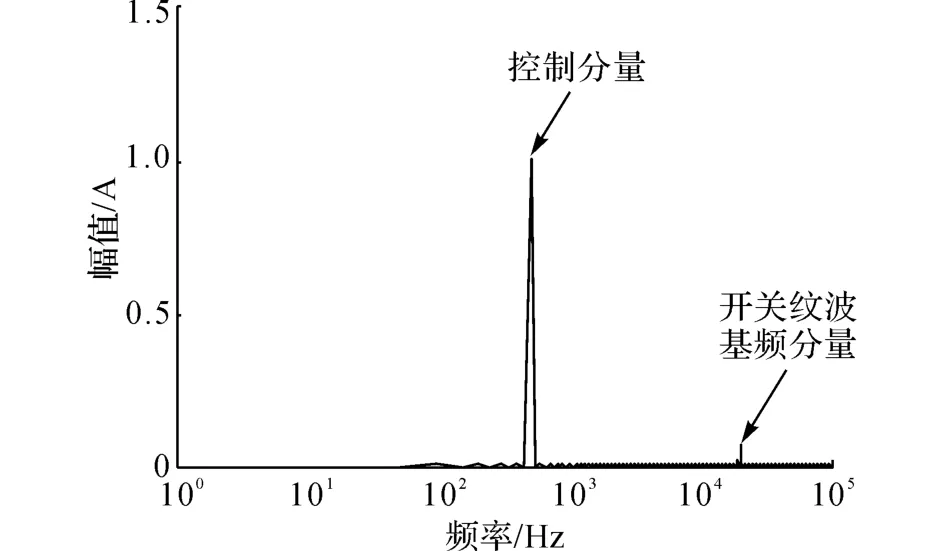
图6 开关功放驱动下的线圈电流频谱Fig.6 Frequency spectrum of coil current when driven by switching power amplifier

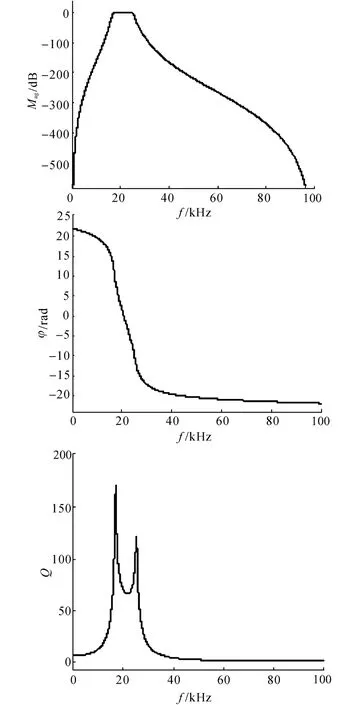
图7 IIR 带通滤波器的频域特性Fig.7 Frequency characteristics of IIR band pass filter

2.2 基频纹波分量幅值I1 的提取

基频纹波分量幅值I1的提取是位移估计中的关键环节，精度直接影响位移解调器的动态性能.提取I1的传统方法是使用整流滤波模拟电路［13］或绝对值滤波算法［15］，实质是对输入信号正半周中线的包络，与真实幅值相比，该方法的输出存在幅度衰减和相位延迟.尽管幅度衰减可以通过后级电路补偿，但高转速时位移估计值相对实际值的相位延迟会导致系统动态性能的下降甚至造成失稳.另一种方法是直接使用FFT 分析线圈电流来获取纹波基频分量的幅值［16］，但采样频率、分辨率等是制约其动态性能的主要因素.

若将基频分量i1（t）看作为转子位移x 为调制信号的调幅信号，则基频纹波分量幅值I1的提取转化为数字信号处理中的信号包络问题.理想的希尔伯特变换器是一个将90°相移施加到输入信号上的全通滤波器，通过希尔伯特变换［18］可以构建性能优于前述方法的基频纹波分量幅值解调器.

设i1（n）为连续信号i1（t）经过采样、保持后得到的数字信号，通过希尔伯特变换构建解析信号为

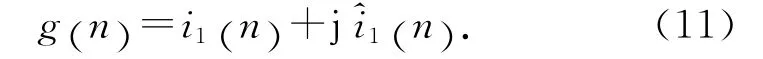
解析信号的幅值为i1（n） 的信号包络，即基频纹波分量幅值为

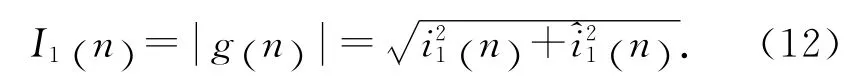
理想希尔伯特变换器的单位冲激响应为

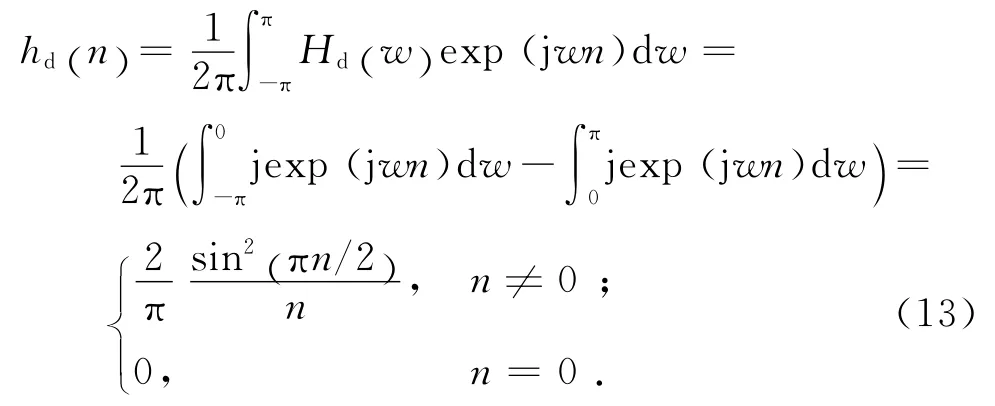
式中：Hd（w）为理想希尔伯特变换器的频率响应，

要实现基频纹波分量幅值的提取，仅须保证希尔伯特变换器的带宽覆盖i1（n）的带宽，可以使用有限冲激响应（FIR）型滤波器实现对理想希尔伯特变换器的近似.选择采样频率Fs＝200kHz，使用Parks-McClellan［19］算 法 设 计 长 度 为30 的 等 纹 波FIR 希尔伯特变换器，变换器的特性如图8所示.

图8中，h（n）表示单位冲激函数，fnorm为归一化频率.使用FIR 希尔伯特变换器构建如图9所示的幅值解调算法.延迟环节的目的是保证信号的同步.

设希尔伯特变换器的输入为调幅信号i1（n）＝［1＋0.5cos（400nπTs）］cos（40 000nπTs），幅 值I1（n）＝1＋0.5cos（400nπTs）中的常数项对应转子位移的静态值，余弦项对应转子以200Hz的频率旋转或振动.图10给出2 种幅值提取方法的仿真结果，整流滤波法中使用的低通滤波器用最优等纹波法设计，采样频率Fs＝200kHz，过渡带为［5kHz，7kHz］，通带增益为0dB，阻带截止频率为-80 dB；希尔伯特幅值解调法使用前述等纹波FIR 希尔伯特变换器.

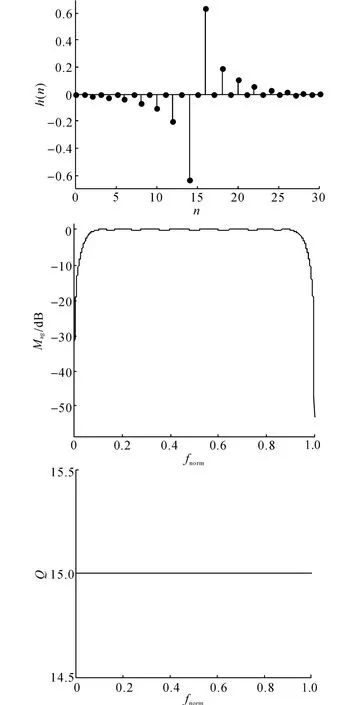
图8 FIR 希尔伯特变换器的单位冲激响应和频域特性Fig.8 Unit impulse response and frequency characteristics of FIR Hilbert transformer

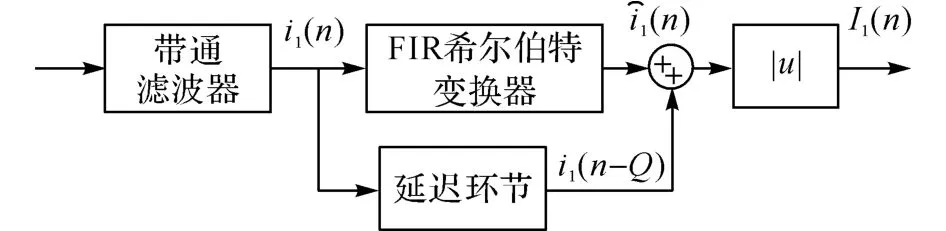
图9 基于希尔伯特变换的幅值解调法Fig.9 Amplitude demodulation algorithms based on Hilbert transform

从仿真结果可以看出，基于希尔伯特变换的幅值提取法的暂态过程短，能够准确地提取基频分量的幅值包络，相位上与实际值基本重合，仅存在对应于群延迟的小时延.采用整流滤波法得到的信号幅值与实际值相比不仅存在信号幅值的衰减，而且存在明显的相位滞后.在对实时性要求严格的电磁轴承系统中后者需要避免，这是以往无传感磁轴承系统在高速时性能下降的一个重要原因.

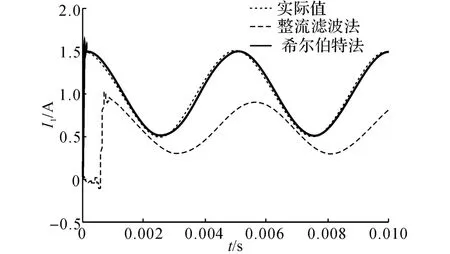
图10 2种幅值提取方法的仿真结果对比Fig.10 Simulation result comparison of two different amplitude demodulation algorithms

3 系统实现和实验结果

3.1 基于FPGA＋DSP的自传感电磁轴承系统

由于自传感电磁轴承系统对实时性的要求较高，传统的数字处理器，如单片机、DSP存在一定的局限性.以4自由度径向电磁轴承自传感运行为例，若考虑系统冗余或磁饱和，则需要同时处理8路线圈电流（传感器）信号.若选取采样频率200kHz和12位AD 转换精度，数据率约为18 Mb／s.对基于指令顺序处理的DSP，多路信号的处理会造成各自由度间控制时序的不一致，且电流信号的实时处理占用了DSP的大量资源，限制了复杂控制算法的使用，也影响了自传感电磁轴承控制系统的实时性.相比之下，基于时钟并行处理的FPGA 更适合多通道信号输入下大数据量的高速处理，能够保证各路输出的时序严格同步.基于以上分析，使用FPGA＋DSP的架构实现自传感电磁轴承系统，将位移估计部分的实时数字信号处理交给FPGA 实现，而控制算法的实现在DSP中完成，系统的结构框图如图11所示.

FIR抽取和低通滤波的作用是下采样和进一步平滑输出.通过FPGA 中的双口RAM 完成与DSP数据交换.开关功放PWM 波的占空比通过DSP的eCAP模块获取.

3.2 实验结果

利用4自由度径向电磁轴承-刚性转子实验平台对基于FPGA 的位置信号解调器的静态线性度和动态性能进行验证.

图11 基于希尔伯特变换的自传感磁轴承系统Fig.11 Hilbert transform based self-sensing AMB system

如图13 所示的实验装置主要包括刚性转子、4自由度径向电磁轴承、电机及变频器、电流型恒频率两电平开关功率放大器、EP4CE15FPGA 信号处理核心、DSP28335控制核心、CWY-DO-81800电涡流位置传感器、fluke i200s电流探头、DL1620数字示波器以及AD／DA 转换和信号调理等辅助电路组成.其中AD 采样使用12位分辨率的AD9226模数转换器，DA 输出采用12 位分辨率的DAC7625数模转换器.实验系统的主要参数如表1所示.表中，m 为转子质量，x0为额定气隙，xp为保护轴承单边气隙.

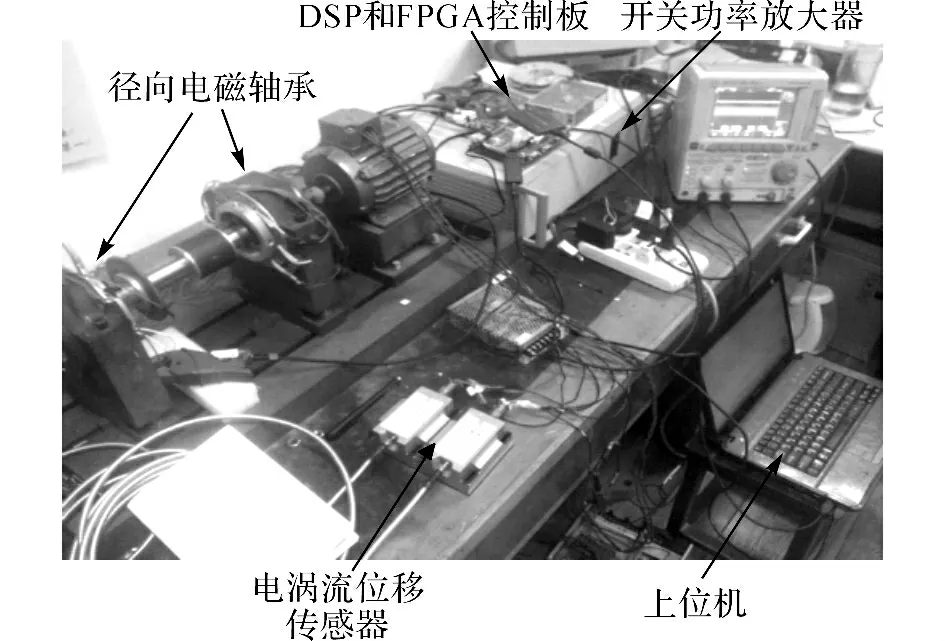
图12 4自由度电磁轴承-刚性转子实验平台Fig.12 4-DOF AMB-rigid rotor experiment platform

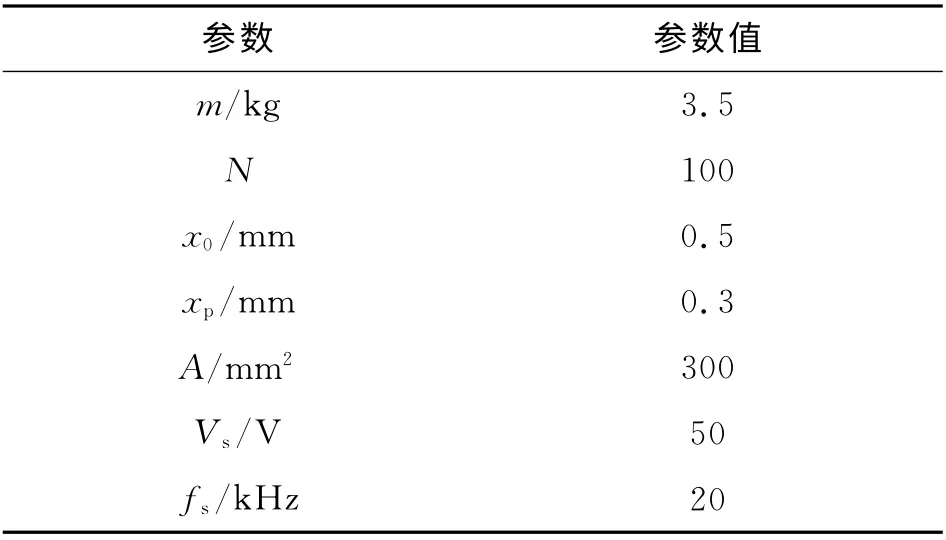
表1 实验平台的主要参数Tab.1 Major parameters of experiment platform

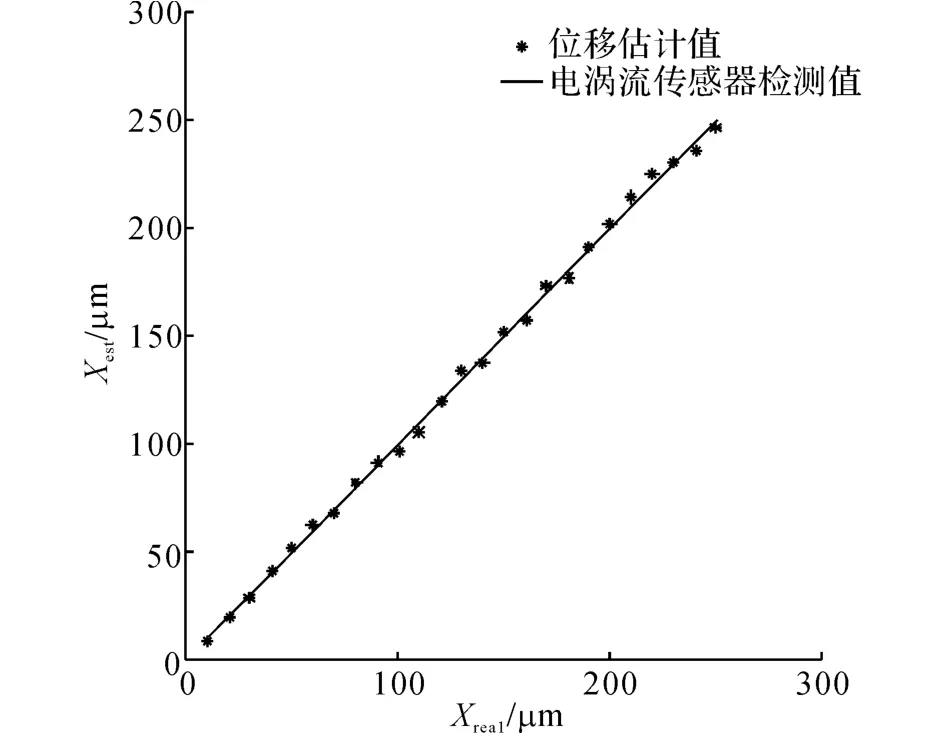
图13 位移估计值与传感器测量值的比较Fig.13 Comparison of estimated and sensor-measured values of displacement

电磁轴承磁极线圈电流通过开关功放板上 的HNC025A 电流传感器获得，经信号调理电路、前置抗混叠滤波器、AD 转换电路输入FPGA，FPGA 的输出为电流纹波基频分量的幅值.FPGA 通过双口RAM 模块将信号输出到DSP 用于控制.DSP 中使用PD 控制算法，通过DA 转换器将控制信号输出到功放，实现转子位移反馈控制.

为了测试本设计的有效性，令转子气隙在0～300μm 的范围内变化，将位移估计器的输出与电涡流传感器的输出进行对比.8极径向电磁轴承在各自由度上定子结构、电路设计具有对称性，因此给出远离电机端电磁轴承垂直方向的线性度测试结果，如图13所示，其余自由度的性能基本一致.

垂直设置在磁极外侧的电涡流位置传感器检测到的位置信号并非磁极中心处的位置信号，但由于所使用的转子是一个刚性转子，通过比例变换可以将涡流传感器检测值转换到磁极中心位置.测试结果表明，位移估计值在测试区间内能够与电涡流位移传感器的值基本吻合，线性度小于5%.

直接使用位移估计值代替电涡流传感器的输出，使用变频器驱动异步电机，转子可以在0～2 000 r／min下维持稳定悬浮.图14 给出在2 000r／min稳定转速下转子的运动轨迹.图中，转子运动轨迹较大 的 原 因 主 要 是 力 回 馈 效 应［13］（force feed-through effect）造成了i1（t）的波形畸变，可以使用参数估计法［6］进行补偿.此外动态运行时开关功放的输出电流中的噪声增大，特别是在开关频率附近的噪声信号会通过带通滤波器，使得位移解调信号中存在扰动.通过电气隔离、屏蔽等措施可以减小这些噪声的干扰.

图14 转速为2 000r／min时转子的运动轨迹Fig.14 Rotor rotation trajectory at 2 000r／min

4 结 语

针对以往自传感主动电磁轴承系统中位移解调算法的不足，根据开关功放驱动下电磁轴承线圈电流的信号特点，本文提出一种基于希尔伯特变换的转子位移估计策略.详细讨论了其中希尔伯特幅值提取的原理和实现过程.通过与以往方法的比较，说明基于希尔伯特变换的电流纹波基频分量的幅值提取算法具有更高的精度和更小的相位滞后.此外，针对自传感电磁轴承系统中多路信号实时处理的特点，提出FPGA＋DSP 结构的系统实现方案，利用FPGA 并行运算的特点保证了各自由度位移估计信号的时序同步.最后，在4自由度径向电磁轴承-刚性转子系统平台上进行实验，验证了上述方法的可行性，实现了两自由度径向电磁轴承在0～2 000 r／min下的自传感稳定运行.

（

）：

［1］SCHWEITZER G.，MASLEN E.Magnetic bearings：theory，design，and application to rotating machinery［M］.［S.l.］：Springer，2009.

［2］LEFANTE V S.Noncollocation in magnetic bearings for flexible rotors［D］.Charlottesville：University of Virginia，1992.

［3］VISCHER D，BLEULER H.A new approach to sensorless and voltage controlled AMB’s based on network theory concepts［C］∥Proceedings of the 2nd International Symposium on Magnetic Bearings.Tokyo：［s.n.］，1990：301-306.

［4］VISCHER D，BLEULER H.Self-sensing active magnetic levitation ［J］.IEEE Transactions on Magnetics，1993，29（2）：1267-1281.

［5］MATSUDA K，OKADA Y，TANI J.Self-sensing magnetic bearing using the principle of differential transformer［C］∥Proceedings of the 2nd International Symposium on Magnetic Bearings.Kanazawa：［s.n.］，1996：107-112.

［6］NOH M D，MASLEN E H.Self-sensing magnetic bearings using parameter estimation［J］.IEEE Transactions on Magnetics，1997，46（1）：45-50.

［7］YIM J S，KIM J H，SUL S K，et al.Sensorless position control of active magnetic bearings based on high frequency signal injection method［C］∥Proceedings of the 18th Annual IEEE APEC.Miami Beach：［s.n.］，2003：83-88.

［8］SCHAMMASS A，HERZOG R，BUEHLER P，et al.New results for self-sensing active magnetic bearings using modulation approach［J］.IEEE Transactions on Control Systems Technology，2005，13（4）：509-516.

［9］王军，徐龙祥.磁悬浮轴承转子位移自检测系统研究［J］.传感器技术，2005，24（3）：27-29.WANG Jun，XU Long-xiang.Study on automation detection system of rotor displacement of self-sensing magnetic bearing［J］.Journal of Transducer Technology，2005，24（3）：27-29.

［10］唐明，祝长生.基于占空比补偿的电磁轴承无传感器运行［J］.浙江大学学报：工学版，2013，47（8）：1418-1423.TANG Ming，ZHU Chang-sheng.Research of selfsensing active magnetic bearings based on duty cycle compensation［J］.Journal of Zhejiang University：Engineering Science，2013，47（8）：1418-1423.

［11］LI L，TADAHIKO S，AKIRA S.State feedback control for active magnetic bearings based on current change rate alone［J］.IEEE Transactions on Magnetics，2004，40（6）：3512-3517.

［12］VAN S G，NIEMANN A C，DU R C P.Evaluation of demodulation algorithms for robust self-sensing active magnetic bearings［J］.Sensors and Actuators A：Physical，2013，189：441-450.

［13］NOH M D，MASLEN E H.Self-sensing magnetic bearings driven by a switching power amplier［D］.Charlottesville：University of Virginia，1996.

［14］唐明，祝长生.力扰动对无传感器电磁轴承位移解调的影响［J］.浙江大学学报：工学版，2013，47（4）：698-704.TANG Ming，ZHU Chang-sheng.Influence from force perturbation to position demodulation in self-sensing active magnetic bearing［J］.Journal of Zhejiang University：Engineering Science，2013，47（4）：698-704.

［15］TANG M，ZHU C S，YU J.Self-sensing active magnetic bearing using real-time duty cycle［J］.Journal of Zhejiang University：Science C，Computers and Electronics，2013，14（8）：600-611.

［16］NIEMANN A.Self-sensing algorithms for active magnetic bearings［D］.Potchefstroom：North-West University，2008.

［17］唐明.径向4自由度主动电磁轴承系统的自传感运行研究-基础理论和关键技术［D］.杭州：浙江大学，2013.TANG Ming.Investigation on the self-sensing operation of 4-DOF radial active magnetic bearings-basic theory and key technology［D］.Hangzhou：Zhejiang University，2013.

［18］胡广书.数字信号处理：理论，算法与实现［M］.北京：清华大学出版社有限公司，2003.

［19］MC C，JAMES H，THOMAS W P.A personal history of the Parks-McClellan algorithm ［J］.Signal Processing Magazine，2005，22（2）：82-86.