关于教学“运算律”的思考

张海红

[摘 要]教师教学时要关注知识发生的起点和价值，遵循知识发展的顺序，引导学生经历数学知识发生、发展、形成的过程，使他们的思维之花悄然绽放。

[关键词]数学教学 运算律 教学片断 思考 原点

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）20-028

课前思考：

“运算律”是苏教版小学数学四年级上册的教学内容，主要教学加法的交换律和结合律，教材遵循由易到难的编排原则，先安排教学加法交换律，再安排教学加法结合律。

我们知道，加法运算律的产生是为了解决加法中简便运算的问题，那么，加法交换律和加法结合律到底哪个是实现加法简算的直接要素？这要从小学阶段简便运算的主要形式来分析。小学数学简算的最主要的指导思想是“凑整”，而加法结合律是实现加法运算“凑整”的直接要素。既然如此，学习加法交换律的必要性又在哪里呢？我认为，加法结合律只能解决相邻两个数相加的问题，如果不相邻的两个数要相加，就需要交换加数的排列顺序，这就要用到加法交换律，从而实现不相邻的两个数相加。基于这样的思考，我对教材中的教学顺序进行了改变，即先教学加法结合律，再教学加法交换律。

教学回顾：

（师出示问题情境图，如下）

一共有多少人参加体育活动？

（让学生根据以下自学提示进行自主学习）

①可以这样算： 还可以这样算：

先算出 有多少人。 先算出 有多少人。

②上面两道算式，哪一道计算更简便？

③观察上面的两道算式和计算结果，你有什么发现？

[通过自主学习，学生得出无论从算式表示的意义来看，还是从计算结果来看，（28+17）+23和28+（17+23）都是相等的，但是28+（17+23）的计算更方便。]

师：别小看这个等式，它会引导我们进一步思考。下面，我们就来进一步观察比较，看看这两个算式有什么相同和不同的地方。

生1：这两个算式都是三个数连加，而且这三个加数都分别相同，计算结果也相同。这两个算式的区别就在于运算顺序不同，第一个算式是先把前两个数相加，再和第三个数相加；而第二个算式是先把后两个数相加，再和第一个数相加。

师：根据这个等式，你们能不能大胆地提出一个猜想？

生2：三个数相加，先把前两个数相加，再加另一个数；或者先把后两个数相加，再加另一个数，和不变。

师：这个猜想正确吗？（学生互相看看，不敢明确作答）

师：要验证这个猜想是否正确，怎么办呢？

生：再举一些例子。

师：举例子是一个很好的方法。老师再举三个例子。

课件出示：同桌每人算一列算式，算完后比一比结果是否相同，并说一说每组中哪道算式的计算更简便。

（45+25）+13 45+（25+13）

（22+18）+36 22+（18+36）

21+（39+13） （39+21）+13

（学生得出这三组算式的和分别相等的结论）

师：那么，再回头看看，刚才的猜想正确吗？

生：正确。

师：才举三个例子，就能证明猜想是正确的吗？（学生表现出很疑惑的样子）如果只凭三个例子就想证明一个猜想，那是不严谨的，我们还需要举更多的例子。由于时间关系，课堂上我们就不再举例了，但是前人举了很多例子，证明这个猜想是正确的。猜想一旦被证明是正确的，那么猜想就变成了结论，现在你们能大声地说出的结论吗？（学生踊跃地尝试表述，但总是说得不流利）

师：说不流利不怪大家，因为这段文字确实太长、太麻烦。那么，能不能用简洁的方法把这个结论表示出来呢？比如图形、字母等。[学生出现以下两种方法：（□+○）+△=□+（○+△），（a+b）+c=a+（b+c）。]

师：大家的想法都很好，体现了数学中求简的精神。为了便于交流，数学上规定用字母表示这个规律，你们能给这个规律取个名字吗？（师生讨论后，把这个规律命名为加法结合律）

师：想一想，学了加法结合律有什么用呢？

生：使计算简便。

师[出示29+22+38、14+77+23、24+（26+27）、83+45+17]：你能利用加法结合律，在合适的地方添上括号，使计算简便吗？

师（指83+45+17）：这道题你是怎么想的？

生3：我把83和17结合在一起先算。

师：那把括号加在哪里呢？

生4：先把45和17交换位置，再用加法结合律计算。

师：是这样吗？[课件演示45和17交换位置后用加法结合律计算，即（83+17）+45]

生：是。

师：但是我有个问题，45和17交换位置后，它们的和会发生变化吗？

生：不会。

师：确定吗？你们是怎样想的？

生5：算45+17与17+45的和，再比一比就知道了。

师：有点道理，但是我们说过只用一两个例子来验证是不科学的，对吧？这样，我们来回忆一下，曾经在哪些地方见到过这样的例子？（带领学生一起回忆交换两个加数的位置和不变的例子，如下图）

师：原来这个规律我们早就用过了，能给它取个名字吗？

生6：加法交换律。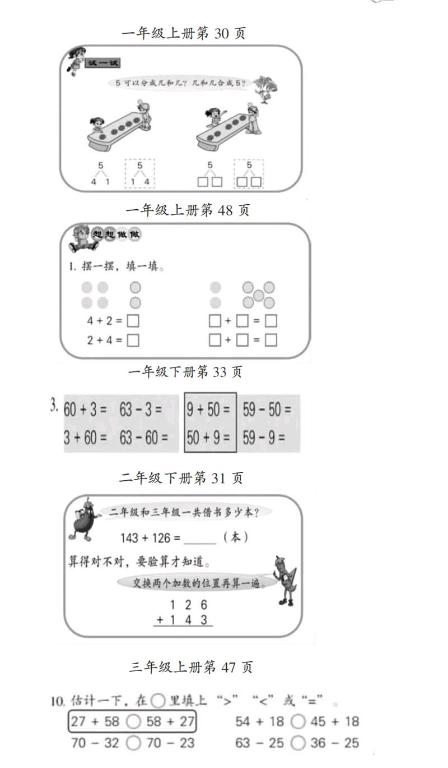

教后思考：

知识的发生、发展都来自于社会和学科本身发展的需要，而数学学科是一门逻辑性极强且极其追求简约的学科。因此，作为数学教师，在教学新内容时往往要追问自己：“为什么要让学生学习这个内容？”例如“比”，用分数和除法都可以对两个数量进行比较，那为什么还要用到“比”呢？比不仅可以对两个数量进行比较，还可以同时对两个以上的数量进行比较。能想到这一点，那么课堂教学设计自然就关注到“比”概念产生的价值。

在本课教学中，我也关注到了运算律产生的意义价值，因此课始就引导学生对“哪个算式算起来更简便”进行比较与思考，并追问“为什么要学习加法结合律”，从而突显了加法结合律的价值。同样的，在教学加法交换律时，有一道练习题是“83+45+17”，学生想要把83和17结合在一起，但仅用加法结合律显然不能达到这个目的，于是自然而然地想到了要把45和17交换位置，这就使加法交换律的价值得到关注。

正因为关注了知识发生的起点和价值，所以我的教学就从教材既定的框架中跳了出来，引导学生经历了数学知识发生、发展的过程，使学生的思维之花悄然绽放。

（责编 蓝 天）