一类具有时滞垂直传播的HIV/AIDS模型的稳定分析

祖克热古丽·吾斯曼，夏米西努尔·阿布都热合曼

(新疆大学数学与系统科学学院，乌鲁木齐 830046)

艾滋病的医学全名为“获得性免疫缺陷综合征”(英文缩写AIDS)，是由艾滋病病毒(人类免疫缺陷病毒－HIV)引起的一种严重传染病。艾滋病病毒侵入人体后会破坏人体的免疫功能，使人体发生多种难以治愈的感染和肿瘤，最终导致死亡。艾滋病病毒对外界环境的抵抗力较弱，离开人体后，常温下只能生存数小时至数天。高温、干燥以及常用消毒药品都可以杀灭这种病毒。据专家介绍，艾滋病病毒感染者从感染初期算起，要经过数年、甚至长达10年或更长的潜伏期后才会发展成艾滋病病人。艾滋病病人因抵抗能力极度下降会出现多种感染，如带状疱疹，口腔霉菌感染，肺结核，特殊病原微生物引起的肠炎、肺炎、脑炎，念珠菌、肺囊虫等多种病原体引起的严重感染等，后期常常发生恶性肿瘤，直至因长期消耗导致全身衰竭而死亡。随着人类对艾滋病认识的加深，越来越多的人开始研究艾滋病，数学家们也不例外。

艾滋病传播方式主要有3种，其中垂直传播(母婴传播)是主要传播形式。文献［1－4］研究了艾滋病垂直传播模型并得到相应的结果。事实上，加时滞的垂直传播模型更接近于实际。因此，本文研究加时滞垂直传播模型。

本文讨论了一类带有时滞垂直传播的HIV/AIDS传播模型，给出了2个平衡点。研究了当R0＜1时无病平衡点全局渐进稳定和地方病平衡点时滞等于零时的全局稳定性。第1部分给出了模型;第2部分证明了解的正性，找出了解集;第3部分求出平衡点和基本再生数;第4部分讨论无病平衡点的稳定性;第5部分研究地方病平衡点的稳定性。

1 模型的建立

本节对 Swarnali Sharma［5］的垂直传播模型增加时滞考虑，建立了一类具有时滞垂直传播的HIV模型，根据条件考虑了模型的2个平衡点的稳定性。当基本再生数小于1时，研究了无病平衡的全局渐进稳定性和地方病平衡点的局部稳定性。

研究中把高危人群分为5种类型:易感者S(t);有症状的感染者I1(t);无症状的感染者I2(t);在接受治疗的感染者T(t);艾滋病患者A(t)。

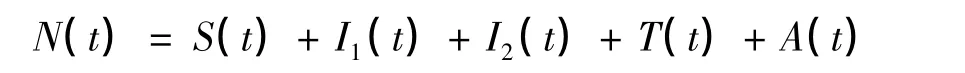
这里，假设易感者和感染者为同性恋且发生率为双线性。根据以上假设得到数学模型为:

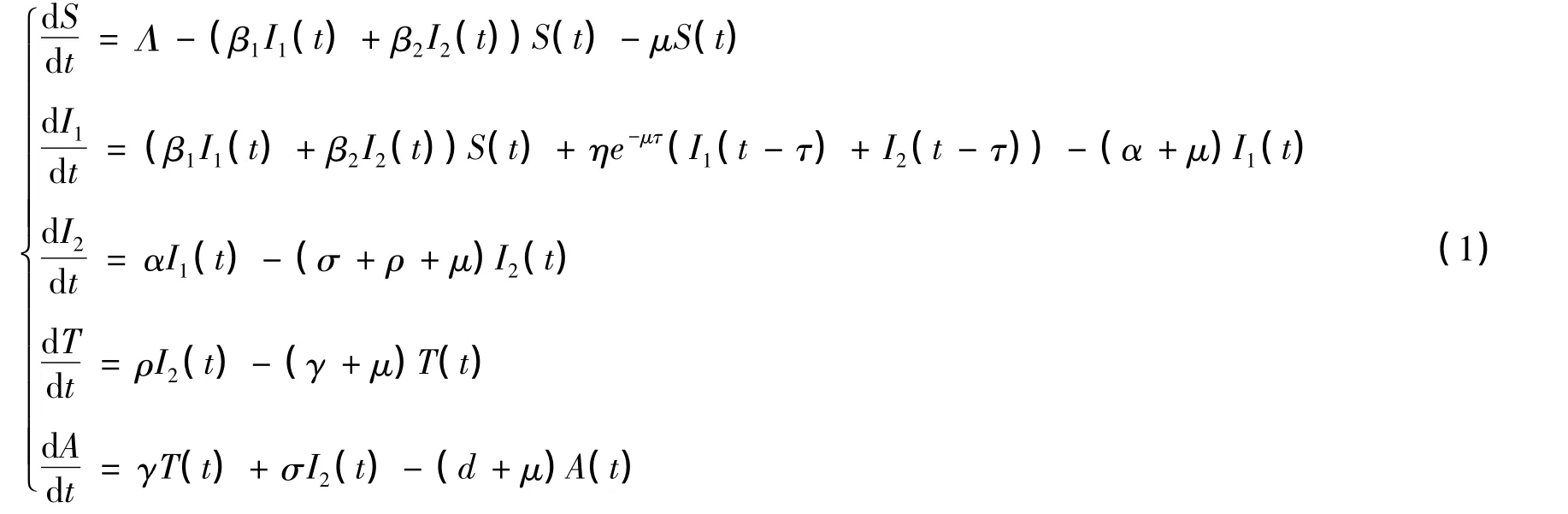
式中:Λ是易感者的输入率;β1是易感者和无症状的感染者接触时的平行传播发生率;β2是易感者和有症状的感染者接触时的平行传播发生率;η是垂直传播率，即新出生的感染的婴儿进入无症状阶段的比例;α是无症状的人群发展到有症状的阶段的比例;ρ是有症状的人群进入接受治疗的感染者人群的比例;σ是有症状的人群直接进入艾滋病患者的比例;γ是接受治疗的人群进入艾滋病患者的比例;d是艾滋病患者的因病死亡率;μ是自然死亡率。

模型(1)的初始条件为:S(θ)=φ1(θ)，I1(θ)=φ2(θ)，I2(θ)=φ3(θ)，T(θ)=φ4(θ)，A(θ)=φ5(θ)，且 φi(θ)≥0，i=1，2，3，4，5，对任意 θ∈［－ τ，0］。由生物意义还可得到 φi＞0，i=1，2。

2 解的正性及解集

定理1 对任意t≥0，在初值条件下，模型(1)的所有解为正解，且所有解进入集合:

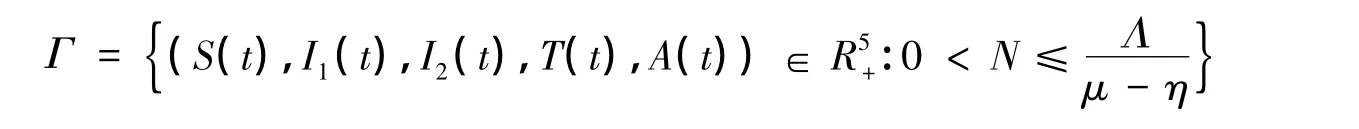
证明 解的正性显然，省略。下面证有界性。

模型(1)的5个方程相加得

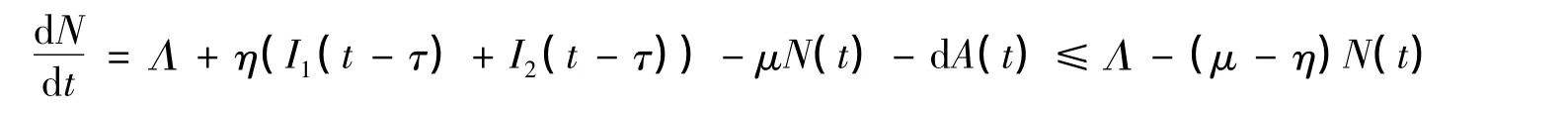
以下讨论始终假设μ＞η。综上可得定理1的结论。

3 平衡点和基本再生数

模型(1)的前3个方程不包含T(t)和A(t)，因此以下只讨论三维的情形:

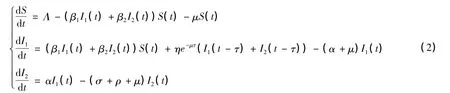
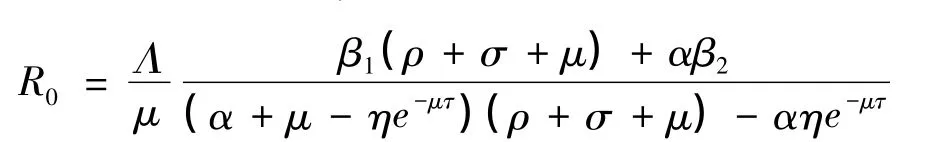
显然，如果R0＞1，则模型(2)存在一个正的地方病平衡点E*=(S*，)，且:

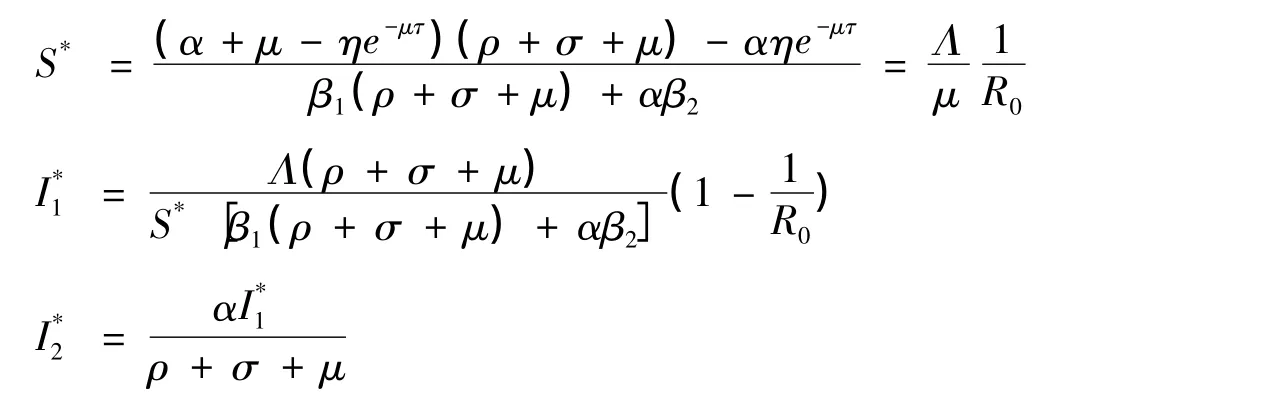
4 无病平衡点的稳定性

定理2 如果R0＜1，那么模型(2)的无病平衡点E0在Γ内局部渐近稳定。

证明 模型(2)在E0处的雅克比矩阵的特征方程为:

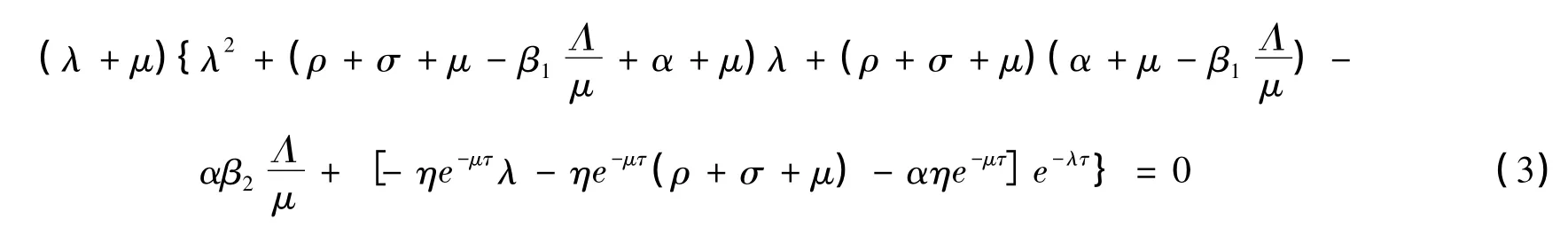
显然一个特正根为λ=－μ。因此，只需讨论如下方程:

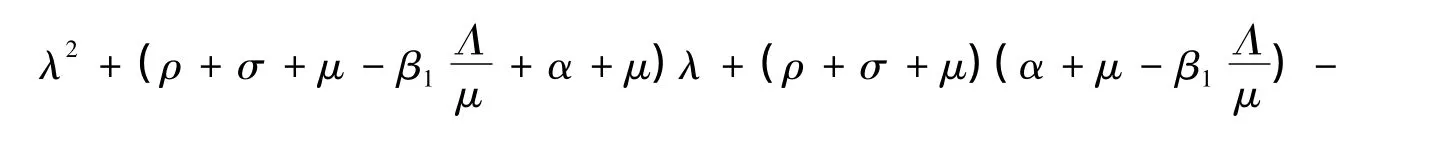
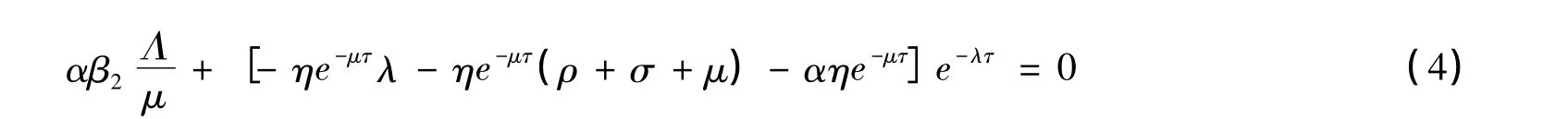
当τ=0时，方程(4)可写成:

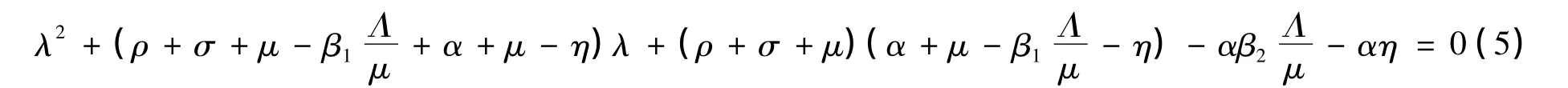
式(5)中令λ的系数为C1，常数项为C2，则由R0＜1可得

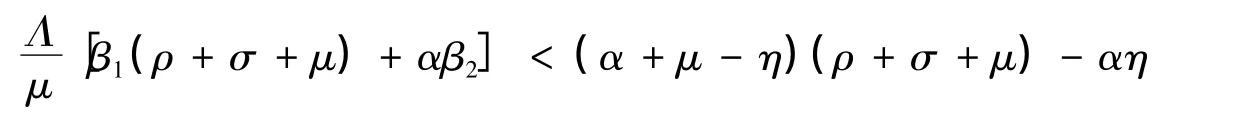
由此可得C2＞0。由

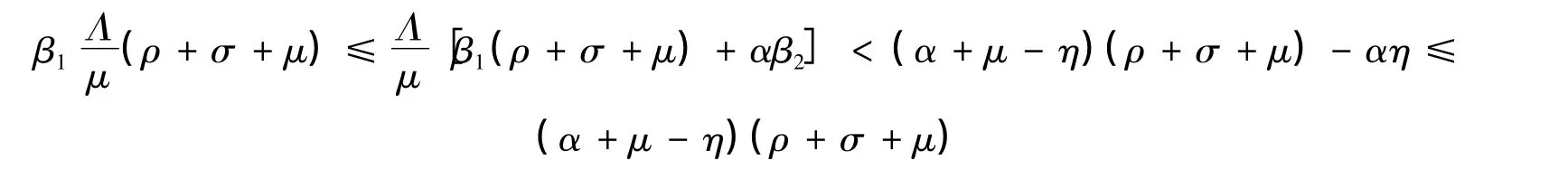
由Hurwitz判据［6］可得:当τ=0时，E0局部渐近稳定。

如果τ＞0，假设(4)存在λ=iω(ω＞0)形式的根，则ω应满足等式

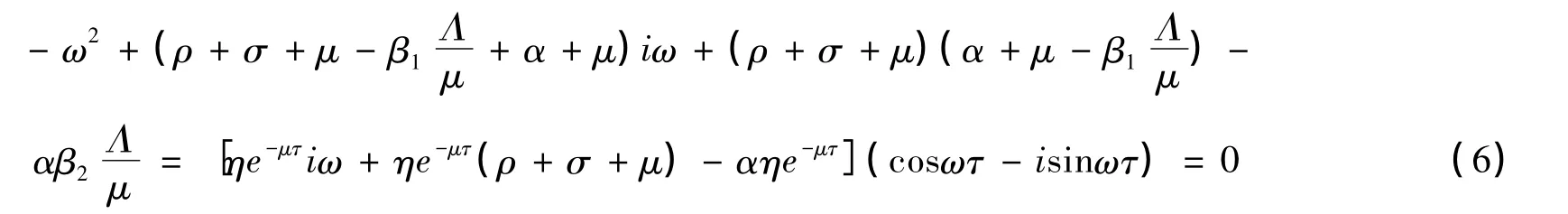
分离实部和虚部得

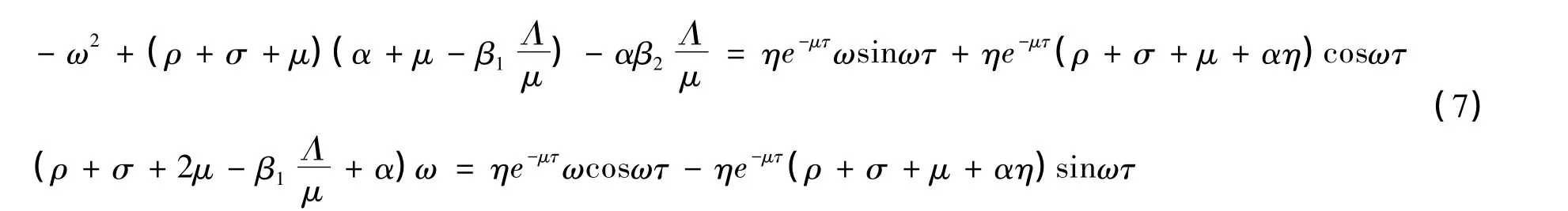
将式(7)的2个方程平方相加得

其中

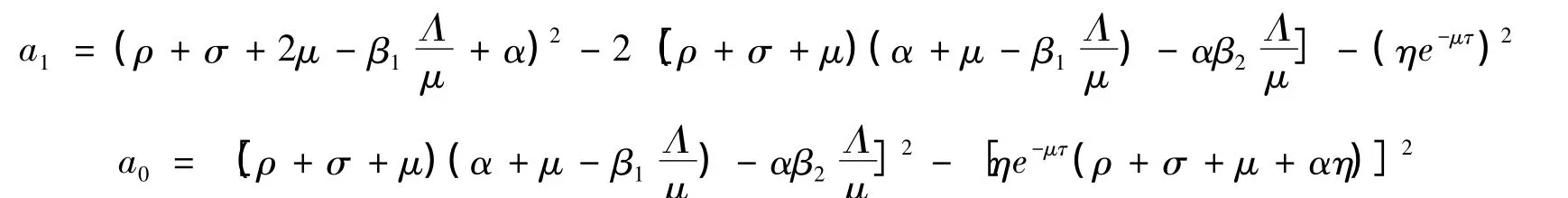
当R0＜1时可得a1＞0，R0＜1意味着

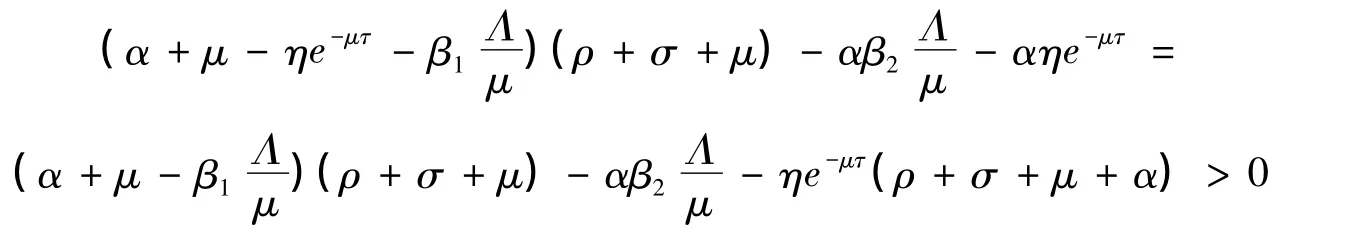
这说明

两边平方后左边刚好是a0，因此方程(8)无正根。这说明方程(4)没有λ=iω形式的根，故其所有根具有负实部。由时滞微分方程一般理论［7－10］知:当R0＜1时，模型(2)的无病平衡点E0是局部渐近稳定的。

下面证明无病平衡点的全局渐进稳定性。

定理3 如果R0＜1，那么模型(2)的无病平衡点E0在Γ内全局渐近稳定。

证明 构造Lyapunov函数如下:

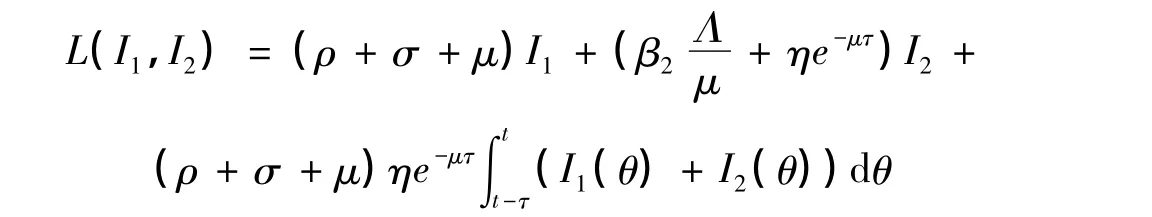
对L沿着模型(2)求导数得

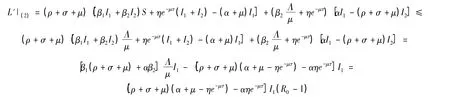
当 R0＜1 时，L'|(2)≤0，等式 L'|(2)=0，当且仅当 I1=0 时成立。因此，集合{(S，I1，I2):L'|(2)=0}的最大不变集为单点集{E0}。由LaSalle不变形原理［5］知:无病平衡点E0在Γ内全局渐近稳定。

5 地方病平衡点的稳定性

本节对τ=0时的模型进行讨论。当τ=0时在文献［5］中已证明了地方病平衡点的局部渐近稳定性。下面用Lyapunov函数的方法证明地方病平衡点的全局渐进稳定性。

定理4 如果R0＞1，那么模型(2)的地方病平衡点E*在Γ内全局渐近稳定。

证明 构造的Lyapunov函数如下，

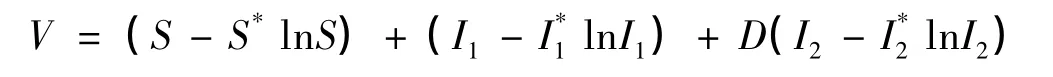
其中D是待定常数。对V沿模型(2)求导得

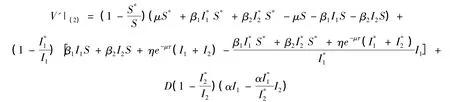
下面进行变量替换，令

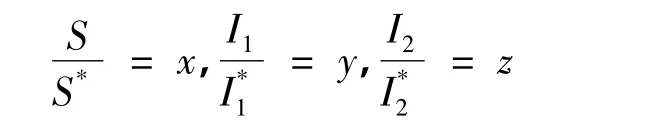
整理可得

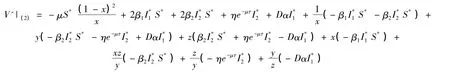
D定义为

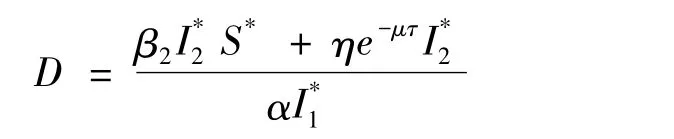
则有

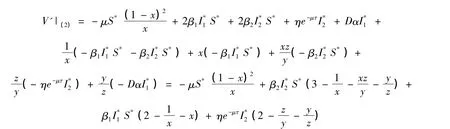
由算数平均数大于或等于几何平均数可得

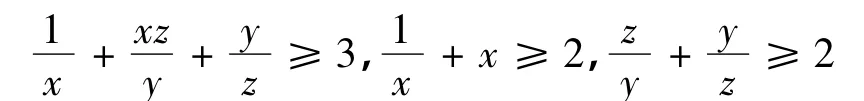
因此，在Γ内有V'|(2)≤0，等式当且仅当x=y=z=1时成立，即S=S*，I1=，I2=。模型(2)集合{(S，I1，I2):V'|(2)=0}上的最大不变集为单点集{E*}。由 LaSalle不变原理［8］知:当 R0＞1时，模型(2)的地方病平衡点E*在Γ内全局渐近稳定。

6 数值仿真

下面通过数值仿真来说明本文结论的正确性和方法的有效性。数值仿真采用Matlab软件。表1和2中的一些参数取自相关文献［5］，另外一些参数由估计所得。

图1、2说明:对于不同的初始值，两类平衡点都是全局渐近稳定的。

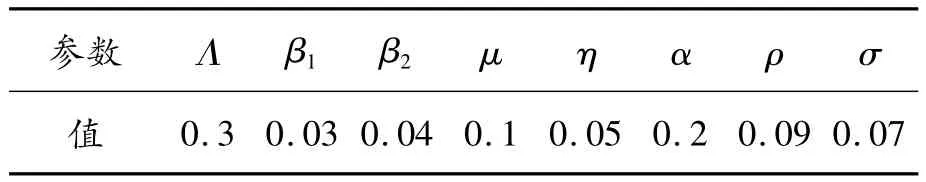
表1 仿真参数1

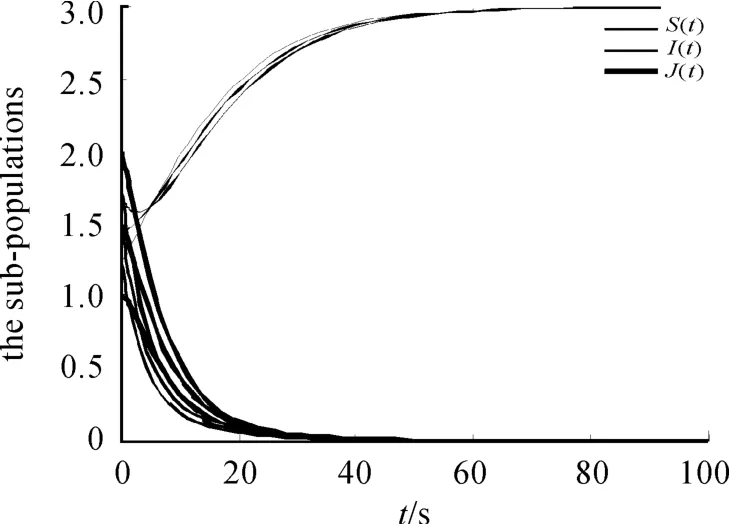
图1 R0=0.607 7

表2 仿真参数2

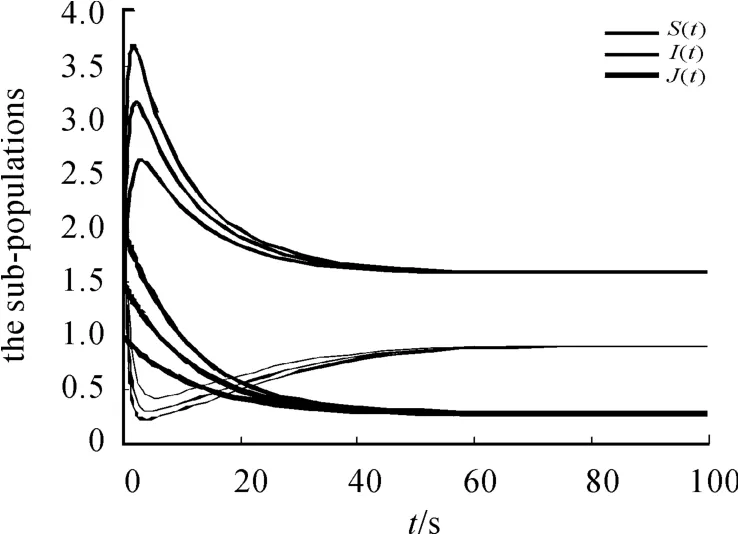
图2 R0=3.698 3

7 结束语

本文研究了一类带时滞垂直传播的HIV/AIDS传播模型的稳定性。微分方程的性态由基本再生数控制。若R0＜1，则无病平衡点全局渐近稳定;当R0＞1且τ=0时，得到了地方病平衡点的全局稳定性;当τ＞0时，通过数值模拟可得地方病平衡点是全局渐近稳定的。其理论证明有待进一步研究。

［1］Naresh R，Sharma D.An HIV/AIDS model with vertical transmission and time delay［J］.World Journal of Modeling and Simulation，2011(7):230 －240.

［2］Naresh R，Tripathi A，Omar S.Modelling the spread of AIDS epidemic with vertical transmission［J］.Applied Mathematics and Computation，2006，178:262 －272.

［3］Liming Cai，Xuezhi Li.Stability analysis of an HIV/AIDS epidemic model with treatment［J］.Journal of Computational and Applied Mathematics，2009，229:313 －323.

［4］Elaiw A M.Global properties of a class of HIV models［M］.Nonlinear Analysis:Real World Applications，2010:2253 －2263.

［5］Swarnali G P.Dynamical Behaviour of an HIV/AIDS Epidemic Model［J］.Differential Equation Dynamic Systems，2014，22(4):369－395.

［6］马知恩，周义仓，王稳地.传染病动力学的数学建模与研究［M］.北京:科学出版社，2004.

［7］Kuang Y.Delay Differential Equations with Applications in Population Dynamics［M］.New York:Academic Press，1993.

［8］LaSalle J P.The Stability of Dynamical Systems，in:Regional Conference Series in Applied Mathematics［M］.Philadelphia:SIAM(Society for Industrial and Applied Mathematics)，1976.

［9］Dongmei Xiao，Shigui Ruan.Global analysis of an epidemic model with nonmonotone incidence rate［J］.Mathematical Biosciences，2007，208:419 －429.

［10］Hai-Feng Huo，Li-Xiang Feng.Global stability for an HIV/AIDS epidemic model with different latent stages and treatment［J］.Applied Mathematical Modeling，2013，37:1480 －1489.