运用改进PSO算法的驾驶员自适应方向与速度综合控制优化研究

邓 涛，卢任之，李亚南，黄希光

(重庆交通大学机电与汽车工程学院，重庆 400074)

目前驾驶员模型主要包括补偿控制模型、预瞄模型以及智能控制模型。补偿控制模型不考虑驾驶员前视作用(即预瞄环节)，而是直接根据当前车辆状态，利用控制算法控制车辆跟随道路轨迹，且系统参数的确定需要大量的实验，效率较低。预瞄模型考虑了驾驶预瞄环节，依据未来时刻车辆理想位置与预估位置的偏差进行控制，包括单点预瞄和多点预瞄模型。其中单点预瞄模型相对控制精度高，但主要针对简单的大曲率工况，模型的通用性不高，不具备学习能力。多点预瞄模型的控制精度较高，但是在很多情况下道路的多点信息难以获取。智能控制模型采用现代控制理论和技术(如模糊、神经网络控制技术)建立驾驶员方向控制模型，不针对特定的道路工况，适应性强。以上已有的驾驶员模型都只是模拟驾驶员行为特点，对于驾驶员熟练操纵汽车在复杂道路上行驶的情形缺乏自调整能力［1］。目前，建立驾驶员的精准数学模型还比较困难。采用模糊PID控制能大体上描述驾驶员驾驶汽车的过程。粒子群(PSO)算法相对于遗传算法思想简单，程序易于实现，需要调整参数少，自调整能力强［2］，但是容易陷入局部最优。因此，本文以行驶误差最小和体力负担最小为优化目标［1］，采用引入变异因子与惯性权重自适应的PSO算法，建立应用单点预瞄算法的改进型PSO优化驾驶员方向与速度控制模型。

1 驾驶员方向控制模型

1.1 改进粒子群算法优化的驾驶员方向模糊PID模型

利用粒子群算法的快速寻优能力体现熟练驾驶员对汽车的操纵过程，遵循驾驶员体力负担最小原则，以理想加速度与实际侧向加速度的误差最小和方向盘转角变化增量最小作为粒子群算法的适应目标函数，对模糊PID控制器系数进行优化［3］。表达式为:

由式(1)、(2)可以建立粒子群算法性能指标函数:

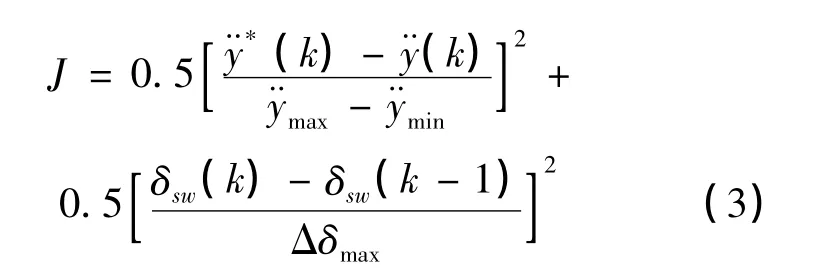
式中:¨y*(k)，¨y(k)分别是k时刻理想侧向加速度和实际侧向加速度;¨ymax，¨ymin是驾驶员所能承受的最大侧向加速度和最小侧向加速度;Δδmax，为前后2个时刻方向盘转角的最大增量;P，Q是跟随误差和转向盘忙碌程度的加权系数，仿真中P，Q均取值为0.5。

根据驾驶员预瞄理论与汽车道路信息，判断驾驶员下一时刻的预瞄点，通过模糊PID控制得出驾驶员的方向盘转角输入增量。模糊PID的差值输入是驾驶员的理想侧向加速度与实际侧向加速度的差值与其变化率。根据方向盘的输入由汽车行驶动力学模型得到汽车的实际侧向加速度。基于改进PSO优化的驾驶员方向模糊PID控制模型如图1所示。

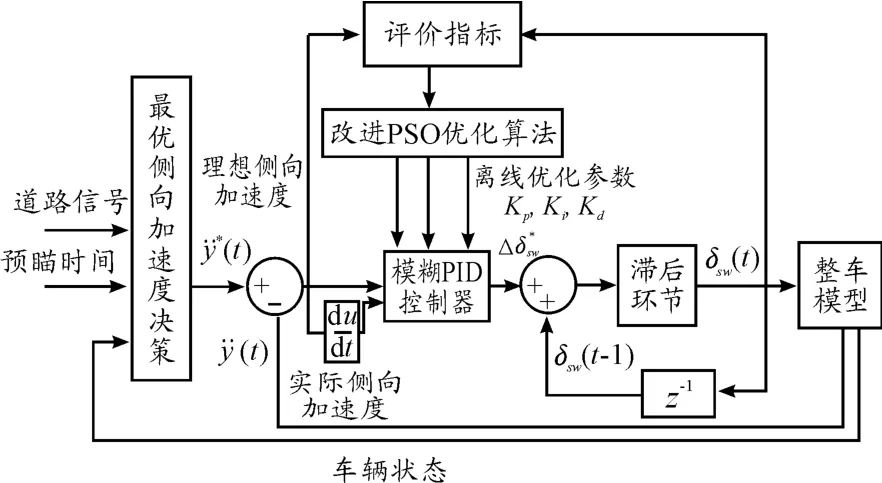
图1 驾驶员方向模糊PID控制模型

1.2 改进的PSO算法(IPSO)

为了解决标准PSO算法在迭代后期容易陷入局部最优的问题，在基本粒子群算法上进行了一些改进。首先，引入变异因子。PSO迭代优化前期搜索速度很快，随着迭代次数的增加，迭代解慢慢接近全局最优解，对应的搜索空间与搜索速度越来越小，此时粒子的更新状态变慢，很容易陷入局部最优。为了克服这个缺陷，引入变异因子。当粒子的最优位置变化很小，如当前后位置差值的绝对值小于0.001时，可认定粒子群陷入局部优化。记录此位置，并以此位置为基础，将10%的粒子重新随机初始化，粒子的位置范围在记录下来的位置的基础上按照变异数值(介于0.05～0.1)随机初始化。其次，增加惯性权重。惯性权重ω对粒子群算法的收敛性有很大影响，ω越大，粒子群的全局优化效果越好，但对应的收敛性变差。因此，为了在获得全局优化效果的同时不影响收敛性，ω的取值应满足迭代初期取值比较大，达到一定迭代次数后取值变小的原则。惯性权重用以下公式进行调节:

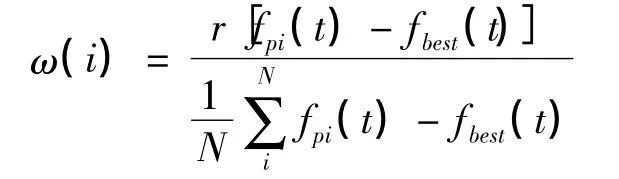
式中:f(t)为种群历史最佳位置的适应值;fpi(t)为第i个粒子个体历史最佳位置的适应值;r为(0，1)范围的常数，;N为种群中粒子个数。以粒子的最佳适应值与种群的历史最佳适应值的“距离”作为惯性权重调节依据。距离越小，则ω越小，集中搜索可保证最优解收敛;距离越大，则ω越大，可保证全局性的搜索。

1.3 IPSO优化模糊PID因子

模糊控制器的隶属度函数的形状是次要的，其论域的个数与其覆盖的论域范围是模糊控制器精确控制的关键。采用改进的粒子群算法对量化因子和比例因子进行优化，调节输出值将不被限制在原有的数量范围内，相当于模糊控制规则数量的增加［4－5］，因此采用改进的粒子群算法对模糊PID的量化因子与比例因子进行优化。以自适应模糊PID控制为基础，利用粒子群算法的自动寻优能力优化驾驶员方向控制模型的总体稳定性操纵评价指标，从而达到准确控制的目的。首先，通过改进PSO算法随机得到一组模糊PID系数;之后借用Simulink命令运行仿真，得到PSO评价指标函数值;再返回PSO算法，判断是否满足迭代终止条件，如果不满足的话，则执行粒子群算法迭代过程，更新粒子的位置信息与速度信息［6］;得到本次全局最优位置后再回到Simulink中进行迭代运算，最终得到最优模糊PID系数。IPSO算法流程如图2所示。

图2 IPSO算法流程

1.4 模糊PID方向控制

模糊PID控制器的输入变量是汽车纵向理想加速度与实际加速度的差值与其差值的变化率，输出变量为驾驶员方向盘转角的增量。因篇幅问题本文只列出代表性的输出变量Ki的隶属度函数曲面，如图3所示。隶属度函数的论域可以调整，以适应模型的变化。

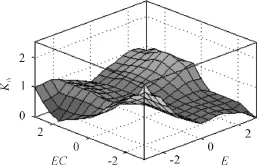
图3 输出变量Ki的隶属度函数

2 驾驶员速度模糊PID控制

模糊PID控制灵活简单，计算量小，简单可靠，鲁棒性好，是一种应用广泛的控制方法。在许多情况下，可以通过调整隶属度函数和选择合适的模糊化与去模糊化方法来实现较好的系统控制［7－9］。驾驶员速度控制模型如图4所示。

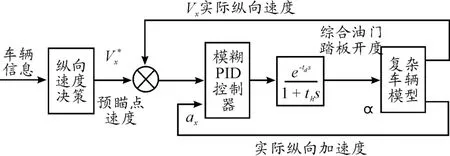
图4 驾驶员速度控制模型

对模糊PID控制器中的参数Kp，Ki和Kd，分别用3个模糊控制器进行在线实时自整定。模糊控制器的输入变量为汽车期望纵向速度与实际纵向速度之间的误差E和误差变化率EC，输出为模糊PID的参数值。代表性的输出变量Kp的隶属度函数曲面如图5所示。

图5 输出变量Kp的隶属度函数

3 方向与速度综合控制

基于IPSO算法的驾驶员方向控制模型以侧向加速度为误差，通过粒子群算法调整模糊PID系数，改变方向盘转角，从而改变车辆纵向位移;以车辆的纵向速度与加速度作为输入，采用模糊PID自适应调整模糊PID的系数，从而调整油门开度，以达到控制汽车速度的目的。将两者结合，在Carsim中建立汽车模型，从而达到对汽车方向与速度综合控制的目的。驾驶员方向与速度综合控制模型如图6所示。

4 建模与仿真分析

驾驶员模型以方向盘转角、油门踏板和制动踏板开度作为控制变量，将驾驶员对制动踏板和油门踏板的操作作用综合为一个统一的物理量来描述，采用统一油门开度表达驾驶员对汽车油门踏板与制动踏板的控制，简化了驾驶员的速度控制模型，并且不考虑复杂的离合器接合、变速器换挡过程，以此实现对车速的控制［10－11］。

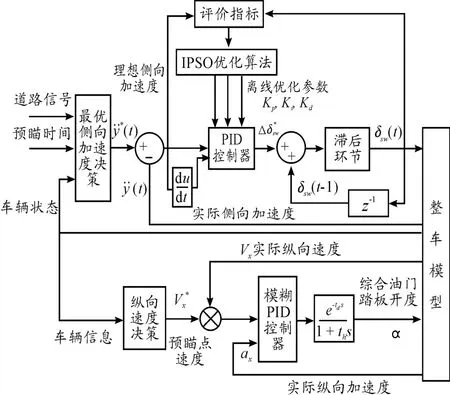
图6 驾驶员方向与速度综合控制模型

4.1 驾驶员方向与速度综合控制优化建模

以方向盘转角、油门踏板和制动踏板开度作为控制变量，不考虑复杂的离合器接合、变速器换挡过程，以此实现对车速的控制。本文采用的道路数据(即理想轨迹)与车速是预知的。采用统一油门开度表达驾驶员对汽车油门踏板与制动踏板的控制。

4.2 典型工况仿真分析

在典型的道路工况(如纵向速度单向变化的侧向双移线工况)和某一大曲率道路工况下验证模型的有效性。仿真中驾驶员的神经反应滞后时间为0.4 s，动作滞后时间为 0.1 s，预瞄时间为1.2 s。

4.2.1 双移线工况仿真

在双移线仿真工况下，纵向速度单向变化，油门开度为负表示是制动。仿真结果如图7所示。

4.2.2 大曲率道路工况仿真

取一组离散的点，运用Matlab插值方法拟合曲线，得到如图8所示的大曲率道路轨迹。将曲线坐标数据输入仿真模型，两种算法理智群规模大小都取300，寻优迭代次数为100。考虑到粒子群取值范围较大，惯性权重初始值选择0.8，其后按照惯性权重公式更新。3个粒子的位置分别代表模糊PID控制器的3个调节参数值。粒子位置更新的学习因子按照经验取值为2。在车速为25 km/h下，仿真对比结果如图8所示。可见改进的PSO模型在较低车速下能够较好地跟随道路中心轨迹。

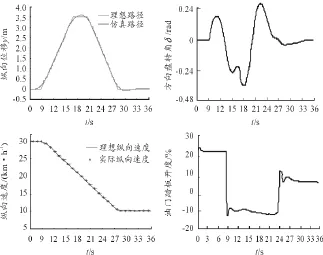
图7 双移线仿真结果

图8 大曲率道路仿真结果

4.2.3 仿真对比

以典型的纵向速度单向变化的双移线工况作为对比，对PSO－模糊PID控制与基于IPSO优化的模糊PID控制做仿真对比分析。两种算法理智群规模大小都取300，寻优迭代次数为100。考虑到粒子群取值范围较大，惯性权重初始值根据优化的效果选择0.8，其后按照惯性权重公式更新。3个粒子的位置分别代表模糊PID控制器的3个调节参数值。粒子位置更新的学习因子按照经验取值为2。结果如图9所示。

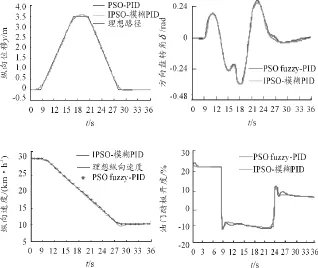
图9 仿真对比结果

从上述仿真结果可以看出:由于是通过算法离线优化获得PID的调节参数，通过大量迭代优化，标准PSO算法与改进的PSO算法都能获得优化的PID参数。本文提出的改进PSO算法与标准的PSO算法的模糊PID方向与速度优化控制均能有效跟随预定的道路轨迹和纵向速度。但是改进的PSO优化模糊PID方法能比较快速地找到合适的PID比例因子、量化因子，效率相对较高，对于不同的道路适应性较强。

IPSO算法适应度函数与标准PSO算法的适应度函数变化曲线如图10所示。从图中可知，IPSO算法由于引入了变异因子与动态惯性权重因子，使其具有更快的收敛速度和更强的全局搜索能力。

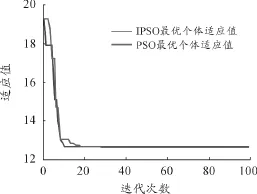
图10 适应度变化曲线

5 结束语

通过建立模糊PID驾驶员方向与速度模型，用改进的PSO(IPSO)智能算法优化模糊PID方向驾驶员模型，以行驶误差最小和体力负担最小为原则，利用其自动全局寻优的能力，对模糊PID因子进行离线迭代寻优，模拟驾驶员从生疏到熟练的驾驶过程，体现了驾驶员的熟练操作能力。

在双移线仿真工况和大曲率道路工况下进行仿真，得到比较好的结果，重合度好。IPSO优化自适应模糊PID能更精准地跟随道路轨迹，控制效果较好。IPSO算法有更快的迭代速度和更好的全局搜索能力，为“人－车－路”系统中驾驶员的建模提供了参考。

［1］丁海涛，郭孔辉，李飞，等.基于加速度反馈的任意道路和车速跟随控制驾驶员模型［J］.机械工程学报，2010(10):116－120.

［2］Mukherjee V，Ghoshal S P.Intelligent Particle Swarm Optimized Fuzzy Pid Controller for Avr System［J］.Electric Power Systems Research，2007，77(12):1689－1698.

［3］段立飞，高振海，王德平.驾驶员对汽车方向的自适应控制行为建模［J］.机械工程学报，2011，47(8):121－133.

［4］Devaraj D，Radhakrishnan T K，Valarmathi K.A Combined Genetic Algorithm and Sugeno Fuzzy Logic Based Approach for on-Line［C］//4th International IEEE Conference“Intelligent Systems”.［S.l.］:IEEE，2008:202－207.

［5］Wu Hongbin，Lou Guohuan.Study of the Fuzzy Pid Control Based on Genetic Algorithm［J］.Chinese Control and Decision Conference，2009(11):6110 －6112.

［6］Juing-Shian Chiou，Shun-Hung Tsai，Ming-Tang Liu.A Pso-Based Adaptive Fuzzy Pid-Controllers［J］.Simulation Modelling Practice and Theory，2012，26:49 －59.

［7］Alessandro Beghi，Marco Liberati，Sergio Mezzalira，et al.Grey-Box Modeling of a Motorcycle Shock Absorber for Virtual Prototyping Applications［J］.Simulation Modelling Practice and Theory，2007，15(8):894 －907.

［8］Juing-Shian Chiou，Kuo-Yang Wang.Application of a Hybrid Controller to a Mobile Robot［J］.Simulation Modelling Practice and Theory，2008，16(7):783 －795.

［9］Kalaba R，Bellman R.Dynamic Programming and Modern Control Theory［M］.［S.l.］:Academic Press Inc，1965.

［10］Ding Haitao，GUO Konghui，LI Fei，et al.Arbitrary Path and Speed Following Driver Model Based on Vehicle Acceleration Feedback［J］.Journal of Mechanical Engineering，2010，46(10):116 －120.

［11］GUO Konghui，DING Haitao，ZHANG Jianwei.Development of a Longitudinal and Lateral Driver Model for Autonomous Vehicle Control［J］.International Journal of Vehicle Design，2004，36(1):50 －65.