汽车动力总成悬置设计优化软件开发

董加加，雷 刚，赖 立，陈华良

(重庆理工大学 a.车辆工程学院;b.汽车零部件制造及检测技术教育部重点实验室，重庆 400054)

现代汽车动力总成并不是刚性地安装在车架上的。在动力总成与车架之间设有悬置系统，动力总成安装在悬置系统之上，由悬置系统支撑动力总成的质量。悬置系统的主要作用是隔振，即尽可能隔离掉动力总成传入车架的振动，同时把车架传入发动机的振动隔离掉［1－3］。此外，悬置系统的橡胶材料有足够的刚度，以免造成动力总成在工作时因摆动幅度过大与相邻部件发生碰撞干涉［4］。动力总成悬置系统的设计、优化理论基本成熟，但是还缺少专门针对汽车悬置系统的设计、优化、分析软件。工程人员通常运用多体动力学软件结合有限元软件来开发、测试悬置系统。这对工程人员的软件操作水平要求比较高，而且由于操作步骤繁琐，容易出错。

本研究将理论与工程实际应用相结合，编写了一套动力总成悬置设计优化软件。针对悬置系统开发，使用该专用软件不仅可以大幅提高开发的效率，而且还具有良好的经济效益。

在悬置系统分析计算的过程中，有些工具如模态计算及解耦率计算等已有大量相关论文进行了介绍［5－6］，故在此不再赘述。

1 软件主界面编写

1.1 主界面的输入参数类型

为了方便软件的使用，要求从主界面中输入的数据都能传入子界面中，这样在子界面中无需重复输入一些通用的数据。这些数据包括发动机的质量及惯性矩、悬置系统的坐标及刚度和欧拉角等。

1.2 主界面编写

主界面必须要做到:有必要的文字说明;界面美观，所有输入类型归类，一目了然。主界面如图1所示。在主界面的右侧是按钮组，单击每个按钮可以分别进入每一个子界面。

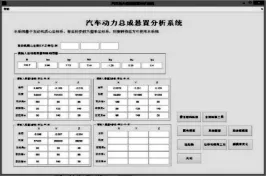
图1 悬置系统设计优化软件主界面

2 坐标系统子界面编写

2.1 悬置系统的坐标定义

在整车坐标系中:原点O位于汽车正前方中间;X轴从车前到车后;Z轴从汽车底部到顶部;Y轴由右手定则确定。在参考坐标系中:纵置发动机原点O位于发动机飞轮靠近变速器一侧的中心;曲轴方向为X轴;从油底壳到汽缸盖为Z方向;Y方向由右手定则确定。在发动机质心坐标系中:原点O位于发动机质心;坐标轴与发动机坐标系平行［7－8］。

2.2 坐标变换及界面编写

根据汽车工程研究院出具的试验报告，在参考坐标系中确定悬置弹性中心位置和质心坐标，在质心坐标系中确定转动惯量和惯性积。由于模态和解耦率计算往往都是在质心坐标系中进行的，故非常有必要单独开发一个坐标转换界面。在数据计算过程中，需要将固定坐标系下的点坐标或者方向矢量转换到连体坐标系或者参考坐标系下。设点P或者一个方向矢量在固定坐标系O－X－Y－Z 坐标系下的值为(PX0，PY0，PZ0)，P在o－u－v－w 坐标系下的值为(PX1，PY1，PZ1)，两者有如下关系［9］:

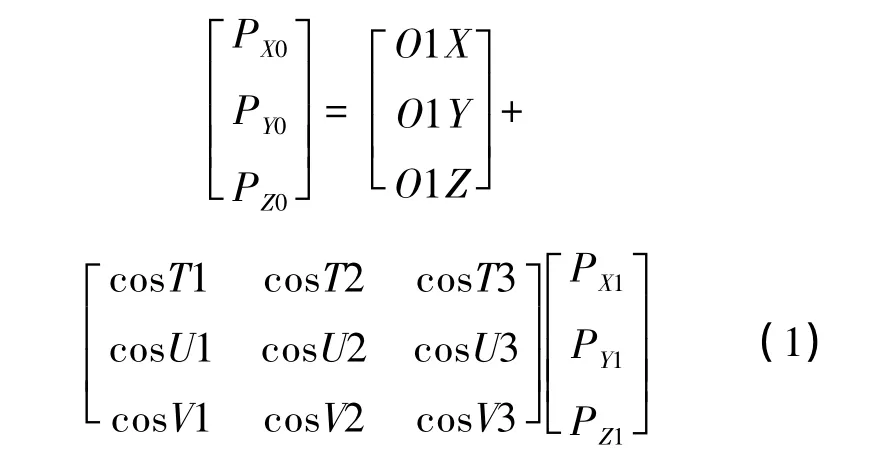
式(1)中:(o1X，o1Y，o1Z)为 o－u－v－w 坐标系原点在坐标系O－X－Y－Z中的坐标值;ou，ov，ow轴与 OX，OY，OZ 轴的夹角分别为 T1，U1，V1，T2，U2，V2，T3，U3，V3。坐标转换工具界面如图 2所示。

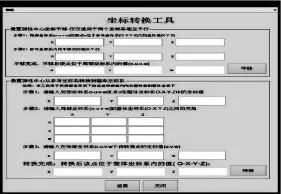
图2 坐标转换工具界面

3 扭矩轴理论及子界面编写

3.1 扭矩轴的理论介绍

扭矩轴是一根无约束的三维刚体旋转轴。由欧拉定理可知，当自由刚体受到某一特定方向的力矩激励时，会绕着某一根轴转动，这个轴为扭矩轴。在动力总成悬置系统中，当施加绕曲轴转动的扭矩时，系统不沿着任何一根主惯性轴转动，而是绕着扭矩轴转动［10］。

假设系统是存在约束的，并且刚体振动的转动位移很小，此时就可以忽略欧拉运动方程中所有的二阶项，从而得到了唯一的TRA方向。在很多的实际场合，TRA不与任何主惯性轴或曲轴的中心线相重合，而常常发生最大到25°的偏离。对于一个实际的动力传动系统来说，如果考虑惯性体是3D非对称形状，并且悬置可以任意安置，则系统的完全解耦是不可能做到的［11］。扭矩轴在动力总成坐标系中的位置可以通过计算得到。定义如下关系:

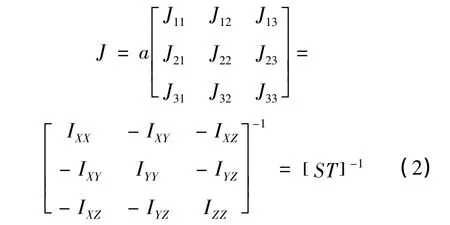
其中a是针对矩阵第1列的规则化常数。

扭矩轴与动力总成坐标系的夹角α，β，γ有如下关系:

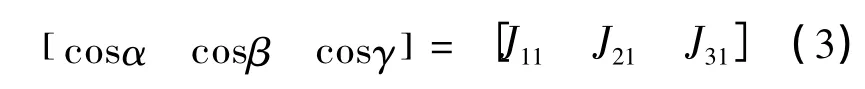
3.2 扭矩轴的计算界面编写

根据上述理论，编写如图3所示的扭矩轴计算界面。此界面中的发动机坐标、转动惯量等参数由主界面传入。以某面包车型为例，其详细数据见表1。依次单击下方的按钮可获得扭矩轴位置和扭矩轴视图等。从界面可以看出，在悬置系统坐标系中，该扭矩轴与X轴夹角为9.6°，与Y轴夹角为99.2°，与Z 轴夹角为87.5°，并且采用彩色符号标出了悬置弹性中心的位置。这样就可以在悬置系统三维CAD模型中画出该扭矩轴。在实际工程试验中，基于扭矩轴在悬置系统空间的位置来对悬置块的位置进行调整，可使系统模态解耦率达到预期要求。

图3 扭矩轴计算界面

表1 某面包车发动机转动惯量 (kg·m2)

4 悬置系统位移和载荷工况(28工况)计算方法及界面编写

4.1 位移和载荷工况相关理论

一个良好的悬置系统必须同时具有良好的限位作用和良好的隔振作用。具有良好的限位作用指的是悬置系统的刚度特性在整体上是非线性的，在悬置系统的小变形阶段需具有较小的刚度，而在大变形阶段则需要具有较大的刚度以抑制发动机的过大位移［12－15］。图4为某面包车型的一个橡胶悬置通过拉伸试验机测试后获得的刚度数据。

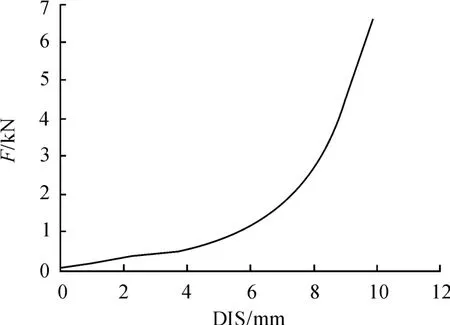
图4 橡胶悬置的拉伸试验刚度数据

由于此刚度曲线为非线性，每个悬置为3条曲线，对应于X，Y，Z三个方向。若要在极限工况下同时找到9条曲线的力－位移的平衡点，用普通求解方法较麻烦，故此处采用迭代法。

定义两个坐标系:一个是原点o在悬置的弹性中心局部坐标系o－u－v－w;一个是原点O在发动机质心的发动机坐标系O－X－Y－Z。由于在本迭代程序编写中同时考虑了其扭转刚度，每个悬置分别具3个线性刚度和3个扭转刚度。首先在坐标系O－X－Y－Z中设发动机受到的外载荷为F，建立发动机－悬置的静平衡方程，各悬置点的位移为:

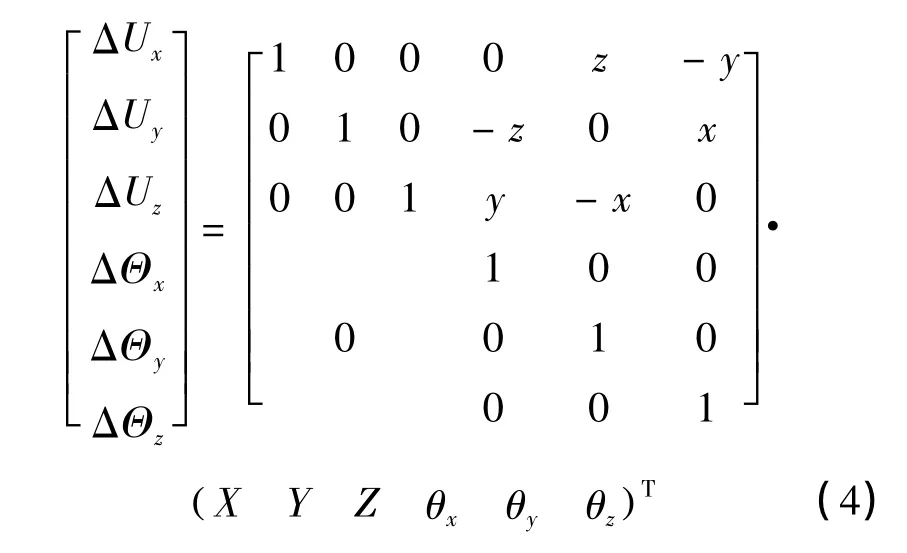
其中:x，y，z为悬置弹性中心在质心坐标系 OX －Y －Z 中的位置;X，Y，Z 和 θx，θy，θz为动力总成的位移。

悬置在质心坐标系O－X－Y－Z中所受的力和力矩为:

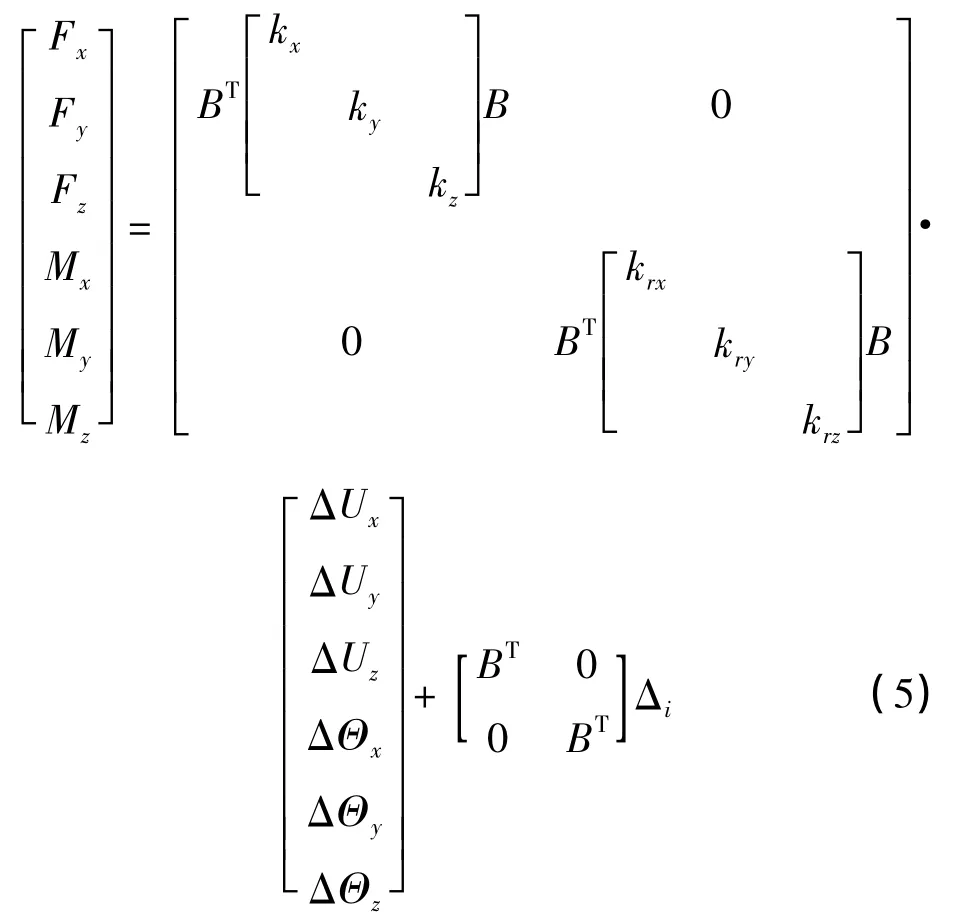
其中:kx，ky，kz为悬置块的拉伸刚度;krx，kry，krz为悬置块的扭转刚度;Δi为悬置在局部坐标系中的偏差修正值;B为局部坐标到发动机质心坐标的方向余弦矩阵。悬置弹性中心将有较小的位移，可以忽略不计。

悬置系统静力平衡方程:

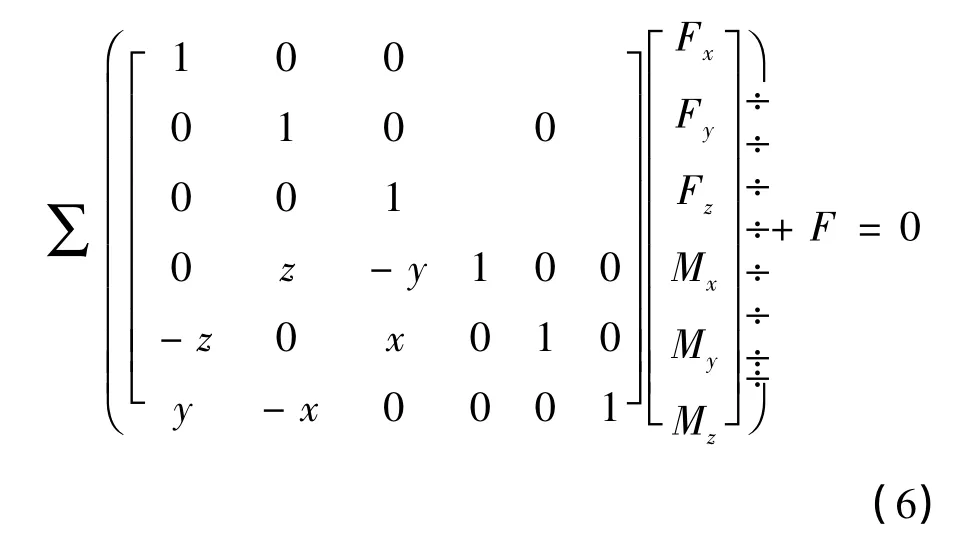
在动力总成质心处施加力和力矩，最终需要输出悬置在各自局部坐标系内的平动位移μ和转动位移φ，由式(7)转换完成。

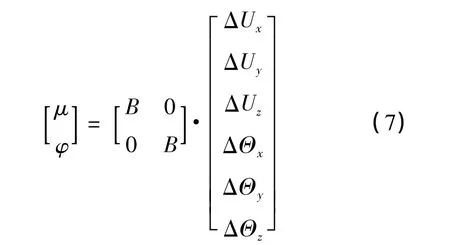
4.2 位移和载荷工况(28工况)的界面编写

基于上述理论，编写出如图5所示的位移和载荷工况计算界面。

图5 位移和载荷工况计算界面

界面设计部分主要考虑到实际工程应用的方便性，在界面中可以直接导入拉伸试验机测试数据，同时输入在每个工况下施加在动力总成上的力和力矩，并且设定一个线性刚度用于初始迭代。按下界面下侧的对应工况的按钮，即可显示计算结果界面。在计算结果界面中可以看到发动机质心位移数据和每个悬置的位移和受力情况，同时也可以监视计算迭代过程是否收敛。

本算例采用28工况中的第5个工况作为演示，该工况的名称为“发动机前进挡最大力矩和+1 g左转”，加载方式如表2所示。即在动力总成质心坐标系内，施加在动力总成质心上Y方向的力为1 420 N，施加在Z方向的力为1 420 N，在动力总成质心上施加的扭矩为－659 N·m。计算结果界面如图6所示。

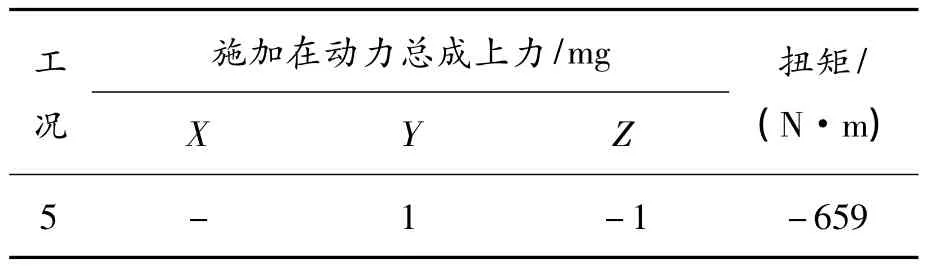
表2 第5个工况加载方式

图6 位移和载荷计算结果界面

通过如图6所示的界面可以获得动力总成质心和悬置弹性中心的变形情况，如表3所示;各悬置弹性中心受力的情况如表4所示。也可以看出本次计算迭代成功，迭代次数为7次。

表3 工况5动力总成质心和悬置弹性中心的变形情况 mm

表4 工况5各悬置弹性中心的受力情况 N

5 结束语

本文对悬置系统开发理论进行梳理，并编写出适合工程实际要求的开发软件，对扭矩轴计算模块、坐标转换模块和位移与载荷工况模块进行了较详细的数学建模，进而编写软件界面。以28工况内的第5个工况为算例对位移和载荷进行分析，得到在该工况下动力总成和各个悬置的变形情况以及该工况下各个悬置的受力情况。

在计算获得各个悬置的受力情况后，即可对悬置的支架刚强度进行分析计算，并以此数据来合理优化悬置支架的形状。

［1］Yu Y H，Naganathan N G，Dukkipati R V.A literature review of automotive engine mount systems［J］.Mechanism and Machine Theory，2001，36:1214 －1216.

［2］廖武，韩全友，张军然，等.动力总成悬置动静刚度的应用与影响因素［J］.客车技术与研究，2014(1):34－36.

［3］余烽，徐中明.基于模拟退火算法的全地形车发动机悬置系统参数优化［J］.四川兵工学报，2013(9):60－63.

［4］刘小平，彭文华.基于Matlab的悬置解耦优化程序开发［J］.汽车工程师，2011(3):22－26.

［5］刘斌，刘钦娅.基于Matlab的发动机悬置系统的固有频率和主振型计算［J］.科研设计，2006(6):24－27.

［6］曾令贤.用MATLAB计算发动机悬置系统的固有频率和主振型［J］.汽车科技，2005(4):27－29.

［7］张保成，苏铁熊.内燃机动力学［M］.北京:国防工业出版社，2009.

［8］刘延柱，洪嘉振.多刚体动力学［M］.北京:高等教育出版社，1989.

［9］上官文斌，贺良勇.汽车动力总成质心与惯性参数测试试验台的开发［J］.振动工程学报，2010(4):119－121.

［10］郭荣，章桐.汽车动力总成悬置系统［M］.上海:同济大学出版社，2013.

［11］Harris C M.Shock and Vibration Hand-book［M］.New York:McGraw-Hill，1995.

［12］赵艳杰.基于Matlab的动力总成悬置系统参数优化设计［J］.机械设计，2009，26(8):62 －65.

［13］上官文斌，徐驰.汽车动力总成悬置系统位移控制设计计算方法［J］.汽车工程，2006，28(8):738－742.

［14］上官文斌，陈大明.带防扭拉杆的动力总成悬置系统位移计算［J］.汽车工程，2012，34(9):798 －805.

［15］Michael Blundell，Damian Harty.Multibody Systems Approach to Vehicle Dynamics［M］.New York:Maple-Vail，Kirkwood，2004.