静电场教学中几个问题的分析

欧阳金华

(曲阜师范大学物理工程学院，山东曲阜 273165)

静电场教学中几个问题的分析

欧阳金华

(曲阜师范大学物理工程学院，山东曲阜 273165)

本文首先给出了静电场中电场强度对任意闭合路径的环量恒为零的理解，任意闭合路径是对实际的宏观静电场问题而言的;接着给出了导体静电平衡问题的理解，静电平衡状态中的导体并非一定是理想导体，放在静电场中的导体只有满足能提供足够的电荷和一定的表面形状两个条件时才能处在静电平衡状态;最后给出了推导介质中高斯定理时应用的极化电荷总量的含义.

环量;通量;静电平衡

静电场的学习是“电磁场与电磁波”，“微波技术基础”等系列课程学习的基础，因此对静电场内容的理解与掌握对整个系列课程的把握具有重要的意义.下面就静电场的几个问题进行分析.

1 静电场环路定理的文字表述

对静电场的环路定理∮cE→·d→l=0，很多教材上，比如文献［1］［2］都用文字表述为静电场中电场强度E→对任意闭合路径的线积分(即环量)恒为零.在最常用的点电荷模型中，若闭合路径过点电荷所在的点时，点电荷位置处的电场强度E→为无限大，怎样计算环量，上述结论还成立吗?初学者很容易对此问题产生困惑.如果讨论此问题时选择点电荷模型，则计算环量时，闭合路径应该绕开点电荷所在的点，因为点电荷位置处的电场强度E→为无限大，无法计算经过这样的点的积分.如果讨论此问题时把点电荷还原为实际电荷的话，则计算环量时闭合路径可任意取，即完全可以通过实际电荷所在的位置.因为几何点的体积为零，实际电荷体密度为有限值，其位置处的电量也为零，电场强度E→为除此几何点位置外的电荷产生的，其位置所对应点的电量是不参与计算的，当然不会出现电场强度E→为无限大的情况了.因此上述结论中的任意闭合路径是对实际的宏观静电场问题而言的.

2 静电场中的导体

静电场中的导体是否一定处在静电平衡状态?静电平衡中导体是否一定为理想导体?对于静电平衡状态，很多文献是这样给出的:导体中含有大量的能够在宏观尺度上自由运动的电荷(自由电子或正负离子);如果有电场存在，由于受电场力的作用，它们在导体内将作宏观上顺或逆电场方向的运动，直至积累在导体表面的电荷产生的附加电场在导体内处处与外加电场相抵消为止;此时，导体内电场处处为零，导体内不再有电荷的宏观移动，称此导体处在静电平衡状态.从定义可知，所谓的静电平衡状态就是指导体内部空间外加场与表面感应电荷(如果有充电电荷的话还包括充电电荷，见文献［2］)产生的附加场相抵消后导体所处的状态.显然，要达到此状态，必须有一定数量的电荷，另外对导体表面的形状也就是电荷分布也应有一定的要求.因为当外加场给定时，并不是任意数量、任意分布的电荷产生的电场都能与其在一定的空间(也就是导体内部的空间)相抵消.因此，从理论上说，并不是任意的导体放入任意的静电场中都能达到静电平衡状态，因为只要物质内部含有大量的能够在宏观尺度上自由运动的电荷(自由电子或正负离子)就称其为导体，对形状没有任何要求.从上述两个条件也可得出，静电平衡状态的达到和保持也不需要一定没有电阻，故静电平衡状态中的导体内部电场强度一定为零，但其并非一定是理想导体.从上述也可得出放在静电场中的导体只有满足能提供足够的电荷和一定的表面形状两个条件时才能处在静电平衡状态，否则处在非平衡状态.通常讨论的静电场中的导体都是在假定满足上述两个条件的基础上进行的.

3 介质中高斯通量定理的推导

文献［1］［3］是这样推导介质中的高斯定理的:将有介质存在时的总电场看成是由自由电荷和极化电荷共同在真空中引起的，则由任意闭合面S穿出的的通量应为

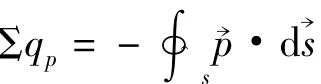
此即为介质中高斯定理的积分形式.

(1)闭合面包围全部的电介质且在介质外时，如图1所示，因电介质为中性，故此种情况体极化电荷和面极化电荷对通量的总贡献为零，即Σqp=0;

(2)任意闭合面S和介质的表面重合时，如图2所示，此种情况所有面极化电荷在S以外，故对通量无贡献，只有全部的体极化电荷有贡献，即

(3)任意闭合面S在介质的内部时，如图3所示，此种情况也是所有面极化电荷在S以外，故对通量无贡献，只有部分的体极化电荷有贡献，即

(4)任意闭合面S穿过部分介质时，如图4所示，此种情况闭合面即包含了部分极化体电荷，也包含了部分极化面电荷，但由极化的机理知，此种情况只有处在介质内部的相关的体极化电荷对通量有贡献，即

而处在介质外部的S2上的

故

第五种情况是闭合面在介质外且相距一定距离，显然此种情况闭合面内没有任何极化电荷，极化电荷总量Σqp=0;第六种情况是闭合面在介质外但包围部分极化面电荷(把图4中S1挪到介质表面就可)，这种情况下闭合面内只有极化面电荷，极化电荷总量

公式形式虽然和第四种情况相同但含义不同.综上所述，推导介质中的高斯定理用到的极化电荷总量，有的情况是仅有极化体电荷提供，有的情况是仅有极化面电荷提供.完全可以借助上述思想把结论推广到空间有多种媒质的情况.也就是说公式(2)适用于空间任意媒质分布的情况.

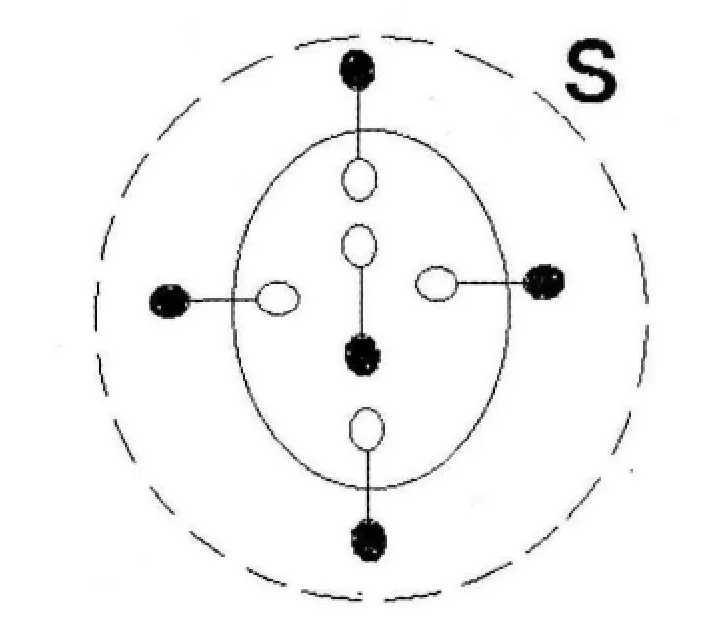
图1 闭合面在介质外的情况

图2 介质表面和闭合面重合的情况

图3 闭合面在介质内的情况

图4 闭合面包围部分介质的情况

4 结束语

通过上面论述给出了三个结论:

(1)静电场中电场强度E→对任意闭合路径的线积分(即环量)恒为零，即∮cE→·d→l=0中的任意闭合路径是对实际的宏观静电场问题而言的，如果选择点电荷模型计算环量时，闭合路径应该绕开点电荷所在的点;

(2)静电平衡状态中的导体并非一定是理想导体，放在静电场中的导体只有满足能提供足够的电荷和一定的表面形状两个条件时才能处在静电平衡状态，否则处在非平衡状态，通常讨论的静电场中的导体都是在假定满足上述两个条件的基础上进行的;

(3)在推导

中用到的极化电荷总量

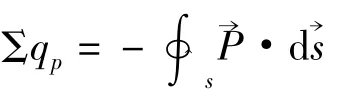
根据闭合面S选取的不同，有的情况是仅有极化体电荷提供，有的情况是仅有极化面电荷提供.

［1］马冰然.电磁场与电磁波(第1版)［M］.广州:华南理工大学出版社，2007.

［2］陈重，崔正勤.电磁场理论基础(第1版)［M］.北京:北京理工大学出版社，2003.

［3］杨儒贵.电磁场与电磁波(第1版)［M］.北京:高等教育出版社，2003.

Some Discussion on the Teaching of Electrostatic Fields

OUYANG Jin－hua
(School of Physics and Engineering，Qufu Normal University，Qufu，273165，China)

The paper gives three discussions.The first one is the understanding on that the circulation of the electric field intensity of an electrostatic field around any closed curve is equal to zero:any closed curve here is only used in actualmacro－electrostatic fields.The second one is about some ideas on the balance of the conductor in electrostatic fields:the conductor heremay be an imperfect electric conductor，it can be balanced only having enough charges and corresponding surface.The last one is giving the meaning of the total polarized charges in the closing surface used in introducing Gauss＇law for dielectrics.

circulation;flux;electrostatic equilibrium

G642.0

A

1672－2590(2015)03－0136－04

2015－04－08

欧阳金华(1974－)，男，山东肥城人，曲阜师范大学物理工程学院讲师.