基于过饱和控制的疏散网络优化模型

任刚，吴建波，华璟怡，姚梦佳，张旻沁

(1.东南大学江苏省城市智能交通重点实验室，南京210096；2.现代城市交通技术江苏高校协同创新中心，南京210096；3.公安部交通管理科学研究所，江苏，无锡214151)

基于过饱和控制的疏散网络优化模型

任刚*1,2，吴建波1,2，华璟怡3，姚梦佳1,2，张旻沁1,2

(1.东南大学江苏省城市智能交通重点实验室，南京210096；2.现代城市交通技术江苏高校协同创新中心，南京210096；3.公安部交通管理科学研究所，江苏，无锡214151)

应急条件下疏散需求呈现短时爆发性特点，为提高网络优化模型在应急疏散状态下的适用性，本文提出了网络过饱和度概念，并结合疏散交通组织策略建立过饱和控制的疏散网络双层优化模型.上层模型从疏散组织者的角度出发最小化疏散网络过饱和度，下层模型以Wardrop用户平衡准则模拟疏散参与者的疏散路径选择行为.采用禁忌搜索算法求解所建模型，并以Sioux Falls网络为平台验证其有效性.实验结果表明，在应急交通疏散状态下，基于过饱和控制的疏散网络优化模型能够实现疏散网络通行能力的最大化利用和应急交通组织策略的最优化配置，具有较强的适用性.

城市交通；疏散网络优化；过饱和控制；交通网络；双层规划模型

1 引言

近些年来，世界各地突发事件的频繁发生给当地造成了巨大的人员伤亡和财产损失.为提高区域疏散效率，降低突发事件造成的损失，有必要对应急疏散的交通问题进行相应研究.

根据美国工程师协会研究结果，应急状态下疏散交通需求的生成具有短时爆发式特性[1]，疏散需求反应曲线如图1所示.疏散0时刻表示发布疏散通知，此前，少部分交通需求自行完成疏散，大量交通需求是在疏散通知发布后短时间内加载至疏散网络，因此在疏散通知发布后一段时间内，城市路网将处于过饱和状态.

现阶段，研究人员对交通网络优化模型已进行相应研究.Sun H等[2]和Gao Z等[3]分别从系统管理者与出行者角度建立双层网络模型对城市网络进行优化设计，并改进了模型求解算法.DesaiSen综合考虑了供需与网络交通分配的平衡，在道路通行能力约束的条件下建立了单层网络优化模型[4]. M iandoabchi等基于网络备用容量理论建立了双层混合整数规划优化模型，并采用模拟退火算法进行求解[5].刘炳全等[6]也对网络设计问题进行了相应研究.

然而上述研究背景为常态交通环境，所建模型均要求路段疏散流量不超过其通行能力，这与疏散网络的过饱和特性相悖.针对这一问题，Liu Y等[7]与LiX等[8]将疏散需求划分为数个阶段，并保证各阶段需求均不超过疏散网络通行能力.这一方法很难保证疏散网络通行能力的充分利用.因此，有必要改进网络优化模型，以实现疏散需求在疏散网络中的一次性加载及交通组织策略的优化配置.

图1 疏散需求曲线[1]Fig.1 Evacuation demand curve

2 网络过饱和度概念与作用

为了定量化描述网络过饱和状态，改进传统网络优化模型以提高模型在网络过饱和状态下的适用性，本文提出网络过饱和度这一概念.网络过饱和度指在不改变路段通行能力限制的前提下，为满足城市交通需求一次性加载的需求，既定道路通行能力矩阵所要叠加的最小乘数，定义式为：

式中xij为路段（i,j）分配的交通流量；Cij为路段（i,j）的通行能力；μij为路段过饱和度；μ为网络过饱和度.

结合图2对这两个概念予以说明.a,b,c,d,e为干路—干路交叉口，l,m,n,k为疏散起点，f为疏散终点，vi为疏散起点i的疏散需求，Cij为路段（i,j）的通行能力.根据图中各路段的通行能力和疏散量，可以得到此时网络过饱和度：

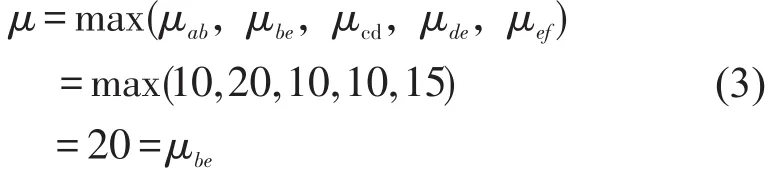
由此可见，整个网络的疏散“瓶颈”路段既不是通行能力最小的路段(c,d)，亦不是疏散量最大的路段(e,f)，而是疏散负荷程度最大的路段(b,e).

图2 过饱和度计算网络Fig.2 Network foroversaturation calculate

网络过饱和度可以定量化描述网络过饱和状态，同时可以快速识别网络上的“瓶颈”路段，有利于疏散管理者对“瓶颈”路段的交通管理；此外，网络过饱和度可以评价不同的疏散交通组织方案，衡量网络的疏散效率.网络过饱和度越低，则表明对应的交通组织方案的疏散效率越高.

3 疏散网络优化模型

针对网络过饱和度可以评价不同疏散交通组织方案、衡量网络疏散效率的特点，结合应急交通组织策略，以疏散网络的过饱和度最低为目标，建立疏散网络双层优化模型.

3.1 疏散网络结构表达

用于疏散网络优化模型构建的相关疏散路网变量与定义如表1所示.

表1 疏散路网变量与定义Table 1 Network variable and notation

用网络集合G=(N,A)代表城市交通网络，如图3所示.

图3 疏散路网表示法Fig.3 Evacuation network representations

网络中普通路段定义为拥有基本通行能力、路段长度和其他出行属性的一般路段；交叉口内部路段则定义为阻抗、长度均为0的特殊路段，以免对交通分配造成影响.

3.2 应急交通组织

反向车道控制是指将对向车道全部或者部分逆向行驶来扩大疏散方向的通行能力以提高网络疏散效率[9]，该策略在美国飓风疏散实践中得到多次应用[10].

冲突消除策略是指通过在交叉口采用特殊的临时性交通管理措施，将主要疏散方向原有的间断交通流转化为连续交通流，减少车辆在交叉口产生的延误，提高网络疏散效率[11].该策略在Xie[10,12]，Bretschneider[13]的疏散网络优化模型中均得到应用.

反向车道控制与冲突消除策略分别从路段与交叉口角度提高路网的疏散效率，二者互为补充[12].因此，建立如图4所示的综合交通组织以提高应急疏散网络的疏散效率.

3.3 双层规划模型

结合应急交通组织，分别从疏散组织者和疏散参与者的角度出发，建立基于过饱和控制的疏散网络双层规划模型.

上层模型（UM）：

目标函数

约束条件

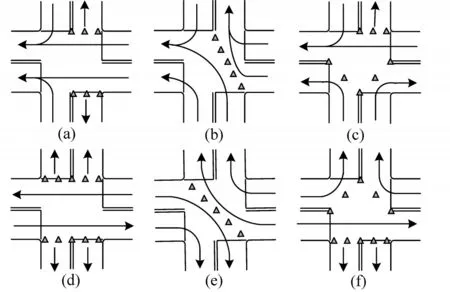
图4 综合交通组织示意图Fig.4 Comprehensive traffic organization

上层模型从疏散组织者角度出发，寻找使得网络饱和度最低的交通组织方案.式(5)为虚拟通行能力约束，用于限制基本路段的疏散交通量使其不超过虚拟通行能力.式(6)–式(8)为反向车道利用约束，式(6)保证路段车道方向的一致性；式(7)保证所有车道均被利用；式(8)保证某方向上车道数为非负.式(9)、式(10)为冲突消除约束，式(9)消除直行车辆与左转车辆的冲突点；式(10)消除交叉口垂直冲突点.式(11)为路段连通性约束，式中M为极大数，描述了路段单向可用车道数与疏散交通量间的内在联系.式(12)为流量非负约束.

下层模型（LM）：

下层模型中从疏散参与者的角度出发进行路径选择.式(14)为流量守恒约束.式(15)为流量转换约束，显示了路径–路段流量间的转化关系.式(16)为流量非负约束.

同时，下层模型式(13)中的行程时间计算引用美国道路局的BPR函数进行计算，计算公式为

4 求解算法

禁忌搜索算法引入了灵活的存储结构，通过禁忌准则与邻域记忆机制来避免迂回搜索，并采用特赦准则保证搜索的多样性，从而实现全局优化.禁忌算法因其搜索多样性与高效性被广泛应用于网络优化模型求解问题.Tuydes等[14]、Xie等[15]利用禁忌搜索算法求解网络优化模型并取得良好效果.

利用禁忌搜索算法求解基于过饱和控制的疏散网络优化模型，具体步骤如下：

Step 1初始可行解的产生.定义禁忌长度、最大迭代步数、最优解滞留步数、精英列表规模，设定迭代步数t=0，构造禁忌列表、搜索列表、精英列表、集约化列表.同时确定网络中各路段交通流量，并且确定初始目标函数值Z(0).

Step 2邻域搜索与更新搜索列表.邻域的候选移动定义为增加、减少路段弧，迭代次数t=t+1，确定搜索列表.

Step 3更新禁忌列表.对候选移动进行比选判断，更新禁忌列表.

Step 4搜索列表检验.若搜索列表非空，转入Step 5；反之，转入Step 9.

Step 5确定候选移动.判断路段弧(i,k)是否属于搜索列表，不属于禁忌列表，决定路段弧(i,k)是否为候选移动.

Step 6更新精英列表与移动.基于相应的目标函数值，并根据Step 1中与Step 2中所得结果中更新目标函数值，并判断是否接受移动.

Step 7搜索列表检验.若搜索列表非空，转入步骤8；反之，转入步骤10.

Step 8终止准则检验.检验迭代次数与搜索列表情况，判断是否满足停止准则.若满足停止准则，算法结束，输出最优解；反之，转入步骤2.

Step 9集约化策略.若搜索列表为空，选取满足特赦准则的禁忌列表中元素，产生新的列表.

Step 10多样化策略.若候选集合不能使目标函数得以优化，且此时搜索列表为空，那么对候选集合进行一定的改进以保证搜索列表中路段移动对目标函数值产生有利影响.

5 示例验证

通过分别采用新建模型与常规疏散网络优化模型对SiouxFalls网络进行优化，对比分析实验结果验证所建模型的有效性.选用的常规疏散网络优化模型亦为双层规划模型，具体模型请参阅文献[12].

5.1 测试网络设计

首先将疏散需求加载于Sioux Falls网络的相关路段中，设置疏散终点为节点20，如图5所示.在网络优化过程中，所有路段均可进行反向车道设置，而交叉口冲突消除策略仅运用于节点8、11、16内.各路段的自由流行驶时间、车道数及通行能力如表2所示.

图5 Sioux Falls交通网络Fig.5 Sioux Fallsnetwork

表2 各路段的交通属性Table 2 Properties of roads

可知，疏散需求量超出测试网络承载能力，常规疏散网络优化模型无法直接求解.为此，根据最大可用疏散时间划分疏散需求，将全部疏散需求加载至疏散路网的时间分别设定为1至10个单位时间（unit，简称U），使每个阶段的疏散需求产生量均可以用常规疏散网络优化模型进行求解.

5.2 结果分析

两类模型在不同加载时间下的网络总旅行时间对比，如图6所示.可知，当疏散需求全部加载至网络的时间为3U时，两类模型的总旅行时间相同.而此时，节点19、21、22与疏散终点（节点20）连接路段的疏散流量等于经过反向车道控制后的路段通行能力.这表明基于过饱和度控制的疏散网络优化模型能够实现疏散网络通行能力的最大化利用.

图6 不同需求加载时间下网络总旅行时间对比Fig.6 Comparison of total travel timewith differentdemand loading time

图6也显示了常规疏散网络优化模型下疏散需求加载至疏散网络的时间对网络疏散总旅行时间的影响.疏散需求加载时间过短，即单位时间内加载到疏散网络的疏散量过大，会导致模型无法得到可行解，反之，则不利于反映疏散时的交通拥堵现象，疏散网络的拥挤效应将会被弱化，使网络总旅行时间减少.新建的网络优化模型不受疏散需求加载至网络的时间影响，更适合在应急疏散条件下应用.

常规网络优化模型控制下的节点8、11、16处的交通组织方案会根据疏散需求加载至疏散网络时间的不同而变化，如图7(a)–7(c)所示.上文提及的当需求加载时间为3U时，对应的交通组织方案如图7(c)所示.此时交通组织方案与新建模型控制下的交通组织方案完全相同，如图7(d).由此可见新建模型可以在应急疏散条件下实现交通组织策略的最优化配置.

图7 不同需求加载时间下交通组织方案对比Fig.7 Comparison of trafficorganizationwith differentdemand loading time

6 研究结论

针对应急疏散需求短时爆发性的特征，本文提出了网络过饱和度这一概念.结合反向车道与冲突消除策略建立了基于过饱和度控制的疏散网络优化模型，以使得网络疏散能力实现最大化利用.最后通过Sioux Falls网络对模型的有效性进行验证.

实验结果表明，该模型有效弥补了常规网络优化模型在网络过饱和状态下适用性不足的缺点，同时可以确定最佳的交通组织方案，提高网络疏散效率，实现网络道路通行能力的最大化利用.如何将过饱和控制与动态交通信息发布相结合告知疏散参与者交叉口交通组织方案将是下一步的研究方向.

[1]Fu H.Development of dynamic travel demandmodels for hurricane evacuation[D].Louisiana State University, 2004.

[2]Sun H,Gao Z,Wu J.A bi-level programmingmodel and solution algorithm for the location of logistics distribution centers[J].Applied Mathematical Modelling,2008,32(4):610-616.

[3]Gao Z,Wu J,Sun H.Solution algorithm for the bi-level discrete network design problem[J].Transportation Research PartB:Methodological,2005,39(6):479-495.

[4]Desai J,Sen S.A global optimization algorithm for reliable network design[J].European Journal of OperationalResearch,2010,200(1):1-8.

[5]Miandoabchi E,Farahani R Z.Optimizing reserve capacity of urban road networks in a discrete network design problem[J].Advances in Engineering Software, 2011,42(12):1041-1050.

[6]刘炳全,黄崇超.一种新的离散型网络平衡设计模型与算法[J].系统工程,2008,26(4):83-87.[LIU B Q, HUANG C C.A novelmodel and algorithm for discrete network equilibrium design[J].Systems Engineering. 2008,26(4):83-87.]

[7]LiuY,Lai X,Chang G L.Cell-based network optimizationmodel for staged evacuation planning under emergencies[J].Transportation Research Record: Journal of The Transportation Research Board,2006, 1964(1):127-135.

[8]Li X,Huang B,Liu Z,et al.A novel method for planning a staged evacuation[J].Journal of Systems Scienceand Complexity,2012,25(6):1093-1107.

[9]Wolshon B.“One-way-out”:Contraflow freeway operation for hurricane evacuation[J].Natural Hazards Review,2001,2(3):105-112.

[10]Xie C,Lin D,Waller S T.A dynamic evacuation network optimization problem with lane reversal and crossing elimination strategies[J].Transportation Research Part E:Logistics and Transportation Review, 2010,46(3):295-316.

[11]Cova T J,Johnson JP.A network flow model for lanebased evacuation routing[J].Transportation Research PartA:Policy and Practice,2003,37(7):579-604.

[12]Xie C,Turnquist M A.Lane-based evacuation network optimization:An integrated Lagrangian relaxation and tabu search approach[J].Transportation Research Part C:Emerging Technologies,2011,19(1):40-63.

[13]Bretschneider S,Kimms A.A basic mathematical model for evacuation problems in urban areas[J]. Transportation Research Part A:Policy and Practice, 2011,45(6):523-539.

[14]Tuydes H,Ziliaskopoulos A K.Tabu-based heuristic approach for optimization of network evacuation contraflow[J].Transportation Research Record,2006, 1964:157-168.

[15]Xie C,TurnquistM A.Integrated evacuation network optimization and emergency vehicle assignment[J]. Transportation Research Record,2009,2091:79-90.

Oversaturation Control-based Model for Evacuation Network Optimization

REN Gang1,2,WU Jian-bo1,2,HUA Jing-yi3,YAOMeng-jia1,2,ZHANGM in-qin1,2

(1.Jiangsu Key Laboratory of Urban ITS,SoutheastUniversity,Nanjing 210096,China; 2.Jiangsu Province Collaborative Innovation CenterofModern Urban Traffic Technologies,Nanjing 210096,China; 3.Traffic ManagementResearch Instituteof TheM inistry of Public Security,Wuxi214151,Jiangsu,China)

A large number of evacuation demands emerged in a short time under the emergency condition. In order to improve the applicability of optimal network design model,the concept of oversaturation of network is proposed.Combined with comprehensive traffic management strategy under emergency conditions,a bi-level network optimalmodelwith oversaturation control is established.The up-levelmodel m inim izes the oversaturation of evacuation network with comprehensive traffic management as the goal of traffic organizers,while the low-levelmodel applies user equilibrium model tom im ic the evacuation routes choice behavior of evacuees.A Tabu Search(TS-based)solution method is used to solve the optimization model.The numerical testswith Sioux Falls network validated the applicability of the bi-level programm ing model.And the results show that the new model can make the best use of network capacity as well as determ ine the optim izing trafficmanagementplanwith betterapplicability underemergency evacuation.

urban traffic;evacuation network optim ization;oversaturation control;transportation network; bi-levelprogrammingmodel

1009-6744（2015）03-0107-07

U491.2

A

2015-01-15

2015-03-06录用日期：2015-03-17

国家自然科学基金资助项目（51278101）；交通运输部建设科技项目（2015318J3308）.

任刚(1976-)，男，浙江上虞人，教授，博士.＊通信作者：rengang@seu.edu.cn