实测冲击负荷建模新方法

秦贞良，贾春娟，张卫星，刘之华（山东大学电气工程学院，济南250061）

实测冲击负荷建模新方法

秦贞良，贾春娟，张卫星，刘之华
（山东大学电气工程学院，济南250061）

针对冲击负荷具有时变性、功率需求主动性以及波动频繁性等特点，本文采用基于实测的冲击负荷模型结构，将多曲线拟合与多目标优化两者相结合，改进了冲击负荷参数辨识的目标函数，提出了一种参数辨识的新方法。在此基础上，用快速非支配排序遗传算法NSGA2（non-dominated sorting genetic algorithm）对实测数据进行参数辨识，得到Pareto解集。研究表明该建模策略能有效地反映冲击负荷的冲击特性，辨识结果与实测数据能较好地吻合，同时也验证了该辨识算法的可行性。

冲击负荷建模；多曲线拟合；多目标优化；参数辨识；非支配排序遗传算法（NSGA2）

电力系统中电弧炉、轧钢机等非线性冲击负荷建模及辨识是电力系统中的重要课题，准确的冲击负荷模型是分析冲击负荷对电网暂态稳定性影响的基础[1-3]。近年来，人们对冲击负荷进行了大量的探索工作并取得成果。文献[4-5]证明了冲击负荷模型最重要的特点是功率需求具有主动性，并给出了一种具有功率自恢复的冲击负荷模型；文献[6]提出了根据实测数据、应用于ATP/EMTP系统的冲击负荷可控电流源模型；文献[7]对电弧炉的非线性特性进行了深入研究，并从其物理机理出发导出了电弧炉电气系统模型，提出了基于非线性系统模型参考自适应控制的分段线性化方法；文献[8]将异步电机动态模型与轧机实际运行功率需求变化规律相结合，提出了体现轧钢机功率需求主动性的周期性冲击负荷模型。

当负荷模型确定后，模型参数辨识就成为负荷建模的核心。传统的辨识方法，如基于梯度搜索或基于随机类等方法，由于存在计算效率低、易陷入局部最优解等缺点，阻碍了其在负荷参数辨识中的应用[9]。为此，模拟进化法在负荷参数辨识领域得到广泛应用，例如粒子群算法、遗传算法等[10-11]。但是，现有参数辨识的算法大都存在一个共同问题，即选取的目标函数单一、且仅能辨识出一组参数。基于上述原因，文献[12]引入了负荷建模的多目标优化，改进了传统负荷参数辨识的目标函数，但采用单曲线拟合参数辨识，不能充分解决冲击负荷时变性及波动频繁性等问题；文献[13-14]讨论了多曲线拟合的参数辨识方法，解决了常规负荷时变性问题，并采用聚类分组算法，将多条扰动曲线进行分类，但选取的是单目标函数且含有电压波动项，未考虑到冲击负荷的功率主动性，且不便于决策者根据不同侧重进行参数选取。这两种方法仅限于对常规负荷建模及参数辨识，针对比较特殊的冲击负荷并不能达到理想效果。

本文在深入分析冲击负荷冲击过程变化曲线特性的基础上，以实测冲击负荷模型为基础，考虑冲击负荷时变性、功率需求的主动性以及波动频繁性等特性，提出了一种基于多曲线拟合与多目标优化两者相结合的新的目标函数。介绍并采用了NSGA2算法实现了冲击负荷的参数辨识，得到Pareto最优解集，实现了冲击负荷模型辨识从特定模型到一般模型、从单一特性到多特性的突破。最后，利用提出的方法，对重庆电网某地区的冲击负荷进行实测分析，结果表明了本文方法的有效性。

1 冲击负荷模型结构和参数辨识

1.1 模型结构分析

本文研究的模型结构包括高压母线以下所有元件的集合。其采用的冲击负荷模型是从电力系统的角度，对实测数据分析后，结合研究具体对象特性得出的。采用文献[5]所提出的冲击负荷模型结构，通过与感应电动机综合负荷模型、感应电动机加恒电流负荷模型以及配网阻抗模型等对比，证明了该模型能较好的描述冲击负荷特性[1，15-16]。

该结构将冲击负荷看作变阻抗负荷，母线电压幅值U为输入激励，母线有功功率P和无功功率Q为输出响应。采用恒电流控制策略，对电压、电流和阻抗采用幂指数拟合，得出一种新的表达式，即

式中：R、X分别为动态电阻和动态电抗；Rs、Xs分别为稳态时的电阻、电抗；Kr、Kx分别为电阻和电抗随电压差变化的系数；U0为电压初始稳定幅值。

结合阻抗表达式并参考自恢复负荷模型[17，18]，得出一种新的冲击负荷模型，即

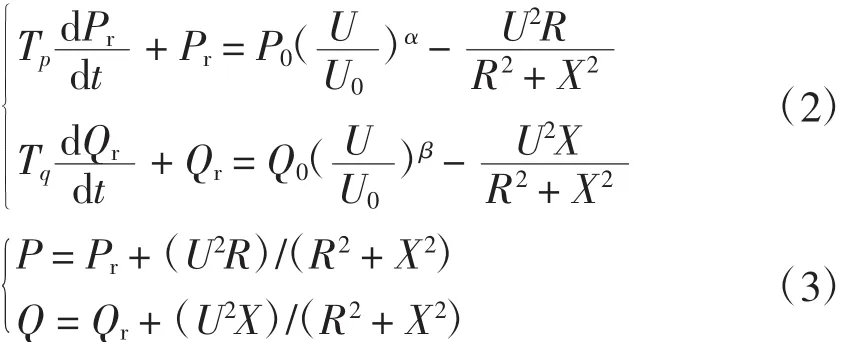
式中：Tp、Tq分别为有功和无功需求的时间常数；Pr、P0分别为负荷有功需求和稳态有功功率；Qr、Q0分别为负荷无功需求和稳态无功功率；α、β分别为稳态时有功和无功指数。

1.2 目标函数值的定义

参数辨识过程实质上是数值优化的过程，进行参数优化需要选取一定的目标函数。对于本文所研究的冲击负荷模型，综合考虑到其本身的时变性、功率需求主动性以及冲击频繁性等特性，提出了基于多曲线拟合、多目标优化的一种新的目标函数。

首先，分别建立单条拟合曲线与实测曲线间的有功无功功率拟合误差函数，即

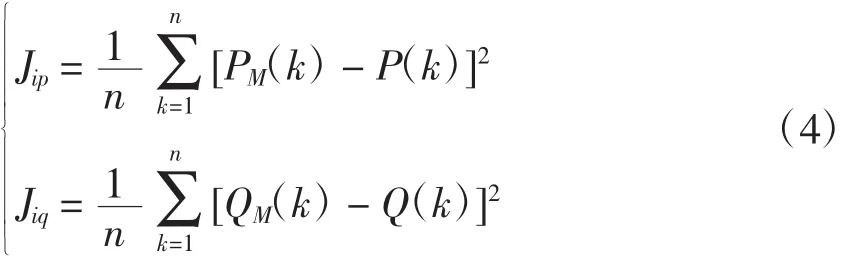
式中：n为每条待测曲线数据长度；i为各量测曲线编号；k为每条曲线的数据点编号；Jip、Jiq为第i条量测曲线有功、无功功率拟合误差；P（k）、Q（k）分别为实测的有功、无功功率数值；PM（k）、QM（k）为该模型输出的有功、无功功率响应。由于考虑到冲击负荷功率主动性的特点，在此未引入电压波动作为输入自变量[13]。

其次，求出每一条量测曲线ai有功、无功的功率均值，即

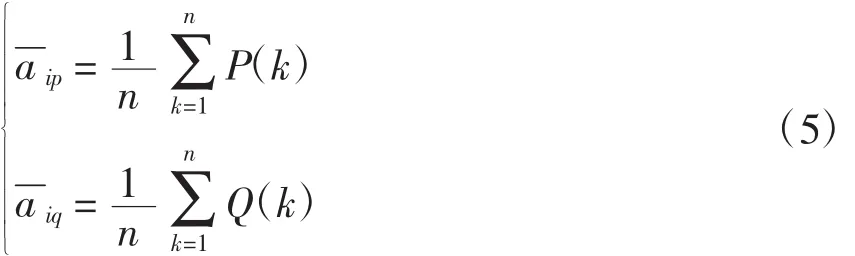
最后，写出基于多曲线拟合和多目标优化的最终表达式，即

式中：m为所测曲线的总数目；Jp、Jq为建立的m条冲击负荷模型输出辨识结果与实测曲线的有功、无功功率拟合误差的平均值，Jp或Jq越小，说明所测曲线总体有功或无功拟合精度越高；min（Jp，J）q为期望的结果，有功拟合误差最小，无功拟合误差也最小，也即形成Pareto解集。

采用多曲线拟合可以解决冲击负荷时变性问题，实现了冲击负荷建模从特定模型到一般模型的突破；采用多目标优化能够避免单目标优化算法对权值的过分依赖，得到的各目标函数值之间关系通过Pareto图直接明了，且可以根据不同的侧重点选择不同的参数。采用具有自恢复负荷模型，体现出了功率需求主动性。

由式（4）～式（6）可知，该模型现在已经转换为一个多目标优化问题，现有的粒子群算法、遗传算法等单目标算法不再适用。为此，介绍一种应用于多目标优化的辨识算法，即NSGA2算法。

2 辨识算法

NSGA2算法[19-20]是遗传算法在多目标优化中的一种典型应用，它采用非支配排序并利用拥挤距离代替适应值共享，计算性能好，运行效率高，而且其解集有良好的分布性，特别是对于低维优化问题，具有较好的表现。多目标优化的主要目的是得到Pareto解集。

2.1 Pareto最优解

对于多目标优化问题，其各个子目标之间一般是矛盾的，也就是使多个子目标一起达到最优值是不可能的。而只能在它们中间进行协调和折中处理，使各个子目标都尽可能地达到满意解。其与单目标优化问题的本质区别在于，它的解并非唯一，而是存在一组由众多Pareto最优解组成的最优解集合，集合中的各个元素称为Pareto最优解或非劣最优解[21]。

2.2 NSGA2算法

NSGA2算法首先对初始种群P0按照遗传算法进行遗传操作，得到种群Q0；再将2个种群合并得到种群R0，在此基础上，进行快速非支配排序和拥挤距离排序选择，形成新种群P′；然后对其采用精英选择策略，不断循环进行直到结束，流程见图1。其算法思想与单目标遗传算法不同之处，主要体现在增加了快速非支配以及拥挤距离排序。对于遗传算法，可以查阅文献[11]等相关资料。

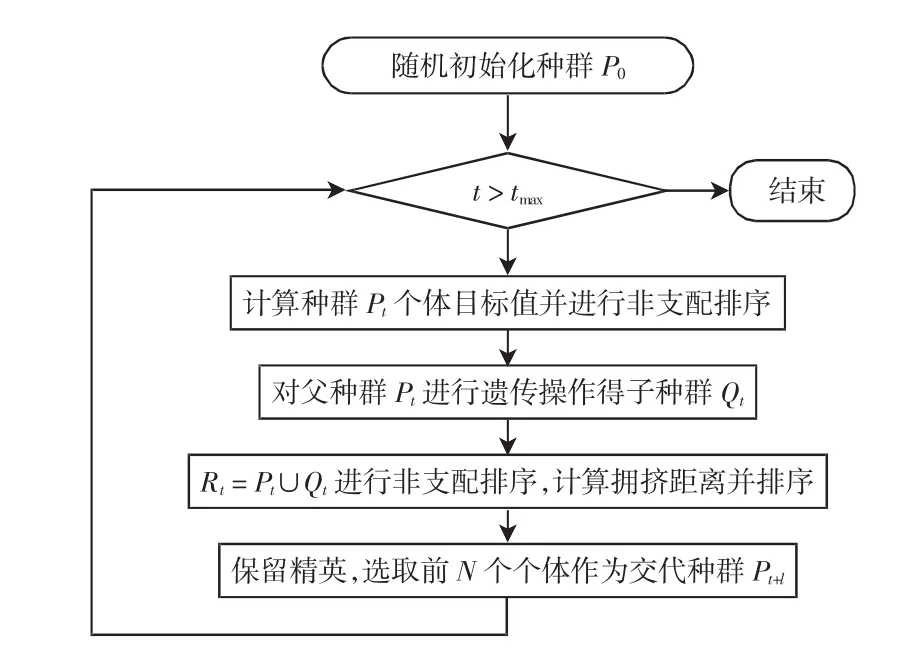
图1 NSGA2算法流程Fig.1 Flow chartof NSGA2

2.3 快速非支配排序

在选择运算之前，需要对种群进行快速非支配排序。该算法需要计算种群Pt中每个个体p的2个参数np和Sp，其中np为种群中支配个体p的解个体数量，Sp为被个体p支配的个体集合.初始化设i=1，Prank=i。首先找出种群中所有np=0的个体，并将它们存入Pareto前端Fi中；对于Fi中每个解q，其所支配的个体集合为Sq，执行nq=nq-i，如果nq=0，则将q保存在中间集合Qt中，此时令i=i+1，Prank=i；如果Qi不为空时，则Fi=Qi。重复以上操作，直到整个种群被分层。

2.4 前端Fi的拥挤距离

为了使Pareto解集尽可能地均匀分布，NSGA2提出了拥挤距离的概念。对每个目标函数，先根据非支配排序集中的解Prank进行排序；然后对每一个解i，计算由解i+1和i-1构成的超立方体的平均边长，即为解i的拥挤距离idistance。其中，边界解的拥挤距离为无穷大。拥挤距离越大，解p的排序越靠前。对种群Pt排序先看快速非支配排序，然后再看拥挤距离，也可以理解为非支配排序优先级高于拥挤距离，只有Prank相等时，才会考虑拥挤idistance排序。

3 应用与算例

表1是2012-11-20重庆电网某地区冲击负荷发生功率冲击时的数据，限于篇幅，仅列出其电压和功率的初值。由表1可知，由于冲击负荷固有的生产特点，冲击负荷发生功率冲击的频率比常规负荷要高得多，24 h内发生波动11次；冲击负荷的初始功率波动范围从最小值52.137MW到最大值70.439MW，负荷存在时变性但变化范围不大。

利用本文所提出的多曲线参数拟合与多曲线优化的目标函数，采用NSGA2算法对表1中的11组实测数据进行参数辨识，辨识得到的Pareto最优解集如图2所示。由图可以看出，NSGA2求得的Pareto最优解集数量足够多且分布均匀；得到的非支配最优解形成了一条凸向原点的曲线，也即所有非支配解的有功与无功相对偏差成反比。采用NSGA2算法运行一次能够得到多个Pareto最优解，为决策者提供了更多的有效参考。图2标示了这组曲线总体上的无功最优、有功最优以及综合最优3个典型情况解时的偏差结果。图中Jp为有功误差量，Jq为无功误差量。

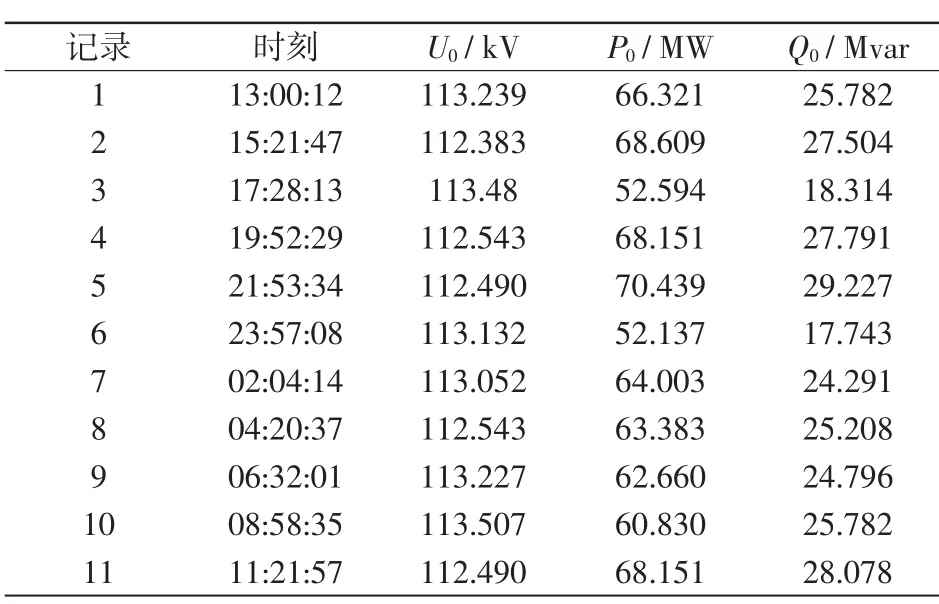
表1 实测负荷数据Tab.1 Field-test load data

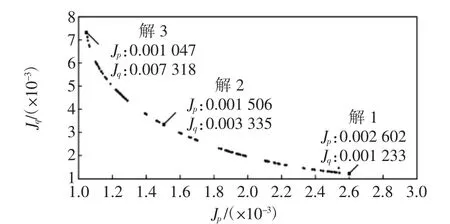
图2 NSGA2的Pareto最优解集Fig.2 Pareto optimalsolution setby NSGA2

实际决策中，当侧重于某一特性时，决策者可以在其较小的Pareto解集中进行选择。表2列出了3种典型情况解下各个参数的辨识结果。解1为无功最优时的情况，此时本组曲线无功拟合误差最小达到0.001 2，有功拟合效果相对误差达到0.002 6。解2和解3分别为拟合综合最优以及有功最优时的情况。

为了体现该方法对具体某一曲线多目标优化的辨识效果，在11组曲线中选取拟合效果最好的一组，采用表2的3种典型参数解，得到其功率拟合效果如图3所示（其中图3中标有实测值的为实测曲线）。

由图3可知，对于综合最优情况是介于有功最优与无功最优之间。当选取有功最优时，其有功拟合效果比较好，但无功拟合误差比较大；当侧重于无功最优时，其有功拟合误差比较大；这也进一步说明了无功与有功偏差成反比，符合图2所示规律。若没有特别的侧重目标，可以选择综合最优，两种偏差都比较小，可以选为最优解。

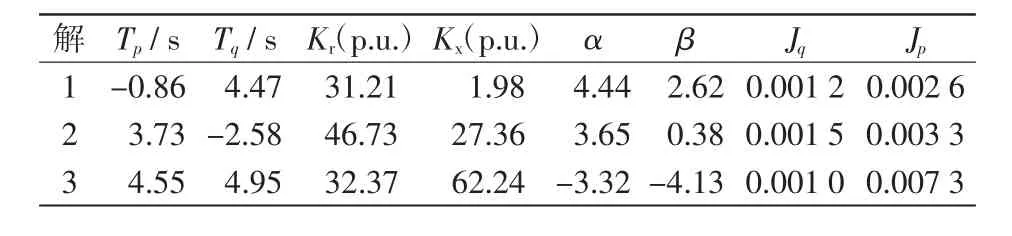
表2 一组典型的Pareto最优解Tab.2 A setof typical Pareto-optimalsolutions

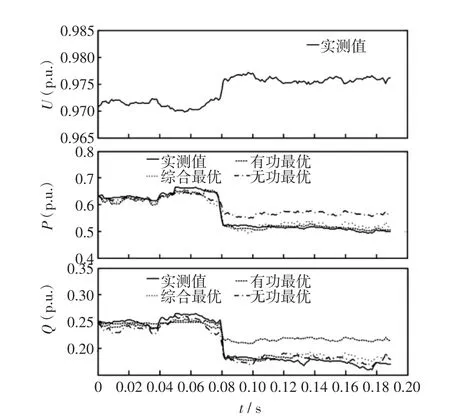
图3 实测曲线与拟合曲线比较Fig.3 CoMparision ofmatching betweenmeasured curvesand fitting ones

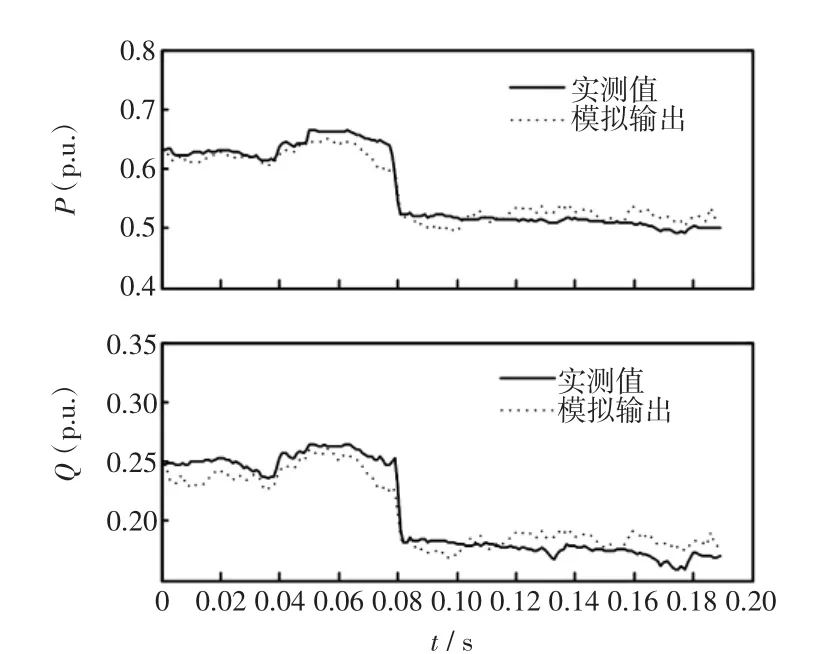
图4 拟合最好的情况Fig.4 Best condition of fitting curves

为了直观地表示采用本方法在多曲线拟合参数辨识算法后的建模精度，选择综合最优情况时的解，以对比的方式形象直观地给出最终建立的冲击负荷模型与实测曲线拟合的情况，最好情况和最坏情况如图4和图5所示。

由图4和图5可以得出，建立的负荷模型是令人满意的。采用本文方法辨识结果总体上能较好地吻合实际曲线，可以满足实际工程应用中的需求。虽针对具体一条曲线拟合，其效果不如单目标曲线，但总体上本方法对多条冲击负荷拟合具有普遍性和代表性，这一点是单曲线单目标拟合所不能比拟的。

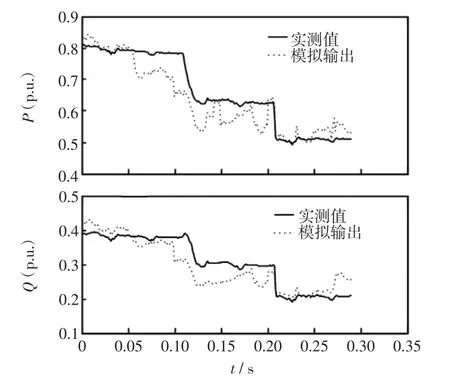
图5 拟合最坏的情况Fig.5 W orst condition of fitting curves

4 结语

冲击负荷与常规负荷相比有其固有特点，对冲击负荷的研究是一个有意义的研究课题。本文基于实测冲击负荷进行建模，充分考虑了冲击负荷的特性，将多曲线参数拟合与多目标优化相结合，提出了一种新的目标函数。采用NSGA2算法对目标函数进行参数辨识，得到冲击负荷模型Pareto可行解集；通过实际辨识结果能较好地吻合实测数据，说明了该目标函数的有效性，验证了该方法的可行性。该目标函数实现了冲击负荷模型辨识从个别模型到一般模型、从单一特性到多特性的突破，既考虑到各冲击负荷的共性，又兼顾了负荷的特性，为冲击负荷参数辨识提供了一条新思路。在辨识过程中也发现，对于长时间段的冲击负荷参数拟合还是有一定的缺陷，主要体现在某些冲击负荷曲线波动变化剧烈，不能很好地拟合出其实际曲线。在后续的研究中可以考虑对冲击负荷进行分组归类，将基于神经网络分组算法应用到多曲线拟合和多目标优化的冲击负荷参数辨识中。

[1]李培强，李欣然，林舜江（LiPeiqiang，LiXinran，Lin

Shunjiang）.电力负荷建模研究述评（Critical review on synthesis loadmodeling）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（5）：56-64， 123.

[2]张红斌，汤涌，张东霞，等（Zhang Hongbin，Tang Yong，Zhang Dongxia，etal）．负荷建模技术的研究现状与未来发展方向（Presentsituation and prospectof loadmodeling technique）[J]．电网技术（PowerSysteMTechnology），2007，31（4）：6-10．

[3]Renmu H，Ma Jin，Hill D J.Composite load modeling via measurementapproach[J].IEEETrans.on Power Systems，2006，21（2）：663-672.

[4]王吉利（Wang Jili）.电力系统特殊负荷建模的研究（Study on Special Load Modeling in Power System）[D].北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2010.

[5]贺仁睦，王吉利，史可琴，等（He Renmu，Wang Jili，Shi Keqin，etal）.实测冲击负荷分析与建模（Analysisand modeling ofshock load viameasurement）[J].中国电机工程学报（Proceedingsof the CSEE），2010，30（25）：59-65.

[6]顾丹珍，艾芊，陈陈，等（Gu Danzhen，AiQian，Chen Chen，etal）．冲击负荷实用建模新方法（A generalmodelingmethod for the impact load）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（20）：10-14．

[7]刘小河（Liu Xiaohe）.电弧炉电气系统的模型、谐波分析及电极调节系统自适应控制的研究（Research on Model and Harmonic Analysis of Arc Furnace Electric Power System，and Adaptive Controlof Electrode Regulator SysteMof Arc Furnace）[D]．西安：西安理工大学自动化与信息工程学院（Xi’an：College of Automation and Information Engineering，Xi’an University of Science and Technology），2000．

[8]李志强，韩志勇，安宁（Li Zhiqiang，Han Zhiyong，An Ning）.体现轧机功率需求主动性的周期性冲击负荷模型（A periodic shock load model incarnating power demand initiative of rollingmill）[J].电网技术（Power SysteMTechnology），2011，35（12）：72-76.

[9]鞠平，马大强.电力系统负荷建模[M].2版.北京：中国电力出版社，2008.

[10]王波，邰能灵，翟海青，等（Wang Bo，TaiNengling，Zhai Haiqing，etal）.基于混合粒子群算法的短期负荷预测模型（Hybrid optimizationmethod based on evolutionary algorithMand particle swarMoptimization for short-terMload forecasting）[J].电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2008，20（3）：50-55.

[11]金群，李欣然，刘艳阳，等（Jin Qun，LiXinran，Liu Yanyang，etal）.一种改进遗传算法及其在负荷建模中的应用（An improved genetic algorithMand its application toloadmodeling）[J].电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2006，18（2）：35-40.

[12]郑漳华，艾芊，冯士刚，等（Zheng Zhanghua，AiQian，Feng Shigang，etal）.负荷建模的多目标优化（Multi-objective optimization for loadmodeling）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（2）：34-38.

[13]石景海，贺仁睦（Shi Jinghai，He Renmu）.动态负荷模型多曲线拟合参数辨识（Parameter identification ofdynamic loadmodelusingmulti-curve fittingmethod）[J].电力系统自动化（Automation ofElectric PowerSystems），2003，27（24）：18-22.

[14]石景海，贺仁睦（Shi Jinghai，He Renmu）.基于量测的负荷建模——分类算法（Measurement-based loadmodeling—sorting algorithm）[J].中国电机工程学报（Proceedingsof the CSEE），2004，24（2）：78-82.

[15]杨超平，贺文，张慧玲，等（Yang Chaoping，He Wen，Zhang Huiling，etal）.宁夏电网安全稳定分析负荷建模（Ningxia power grid security and stability analysis load modeling）[J].电力系统自动化（Automation of Electric Power Systems），2007，31（7）：104-107.

[16]中国电力科学研究院.中国版BPA暂态稳定程序用户手册（3.0）[R].北京：中国电力科学研究院，2005．

[17]周双喜，朱凌志．电力系统电压稳定性及其控制[M].北京：中国电力出版社，2003．

[18]Hill D J．Nonlinear dynamic loadmodelswith recovery for voltage stability studies[J]．IEEE Trans on Power Systems，1993，8（1）：166-176．

[19]Deb K，Pratap A，Agarwal S，etal.A fastand elitistmultiobjective genetic algorithm：NSGA-II[J].IEEE Trans on Evolutionary Computation，2002，6（2）：182-197.

[20]顾晨，乐秀潘（Gu Chen，Le Xiufan）.基于NSGAII的分布式电源优化配置（Optimalallocation ofdistributed generation based on NSGAII）[J].电力系统及其自动化学报（ProceedingsoftheCSU-EPSA），2012，24（4）：130-133.

[21]杨夏雯（Yang Xiawen）.多目标进化算法的改进及其应用研究（Improved Multi-Objective Evolution Algorithms and Their Applications）[D].南京：南京航空航天大学自动化学院（Nanjing：Schoolof Automation Engineering，NanjingUniversityofAeronauticsandAstronautics），2011.

New Modeling Method for Measuring IMpact Load

QIN Zhenliang，JIA Chunjuan，ZHANGWeixing，LIU Zhihua
（Schoolof Electrical Engineering，Shandong University，Jinan 250061，China）

According to impact load with the featuresof time-varying，power demand initiative，and the frequent fluctuation，a newmethod for parameter identification is presented in this paper，which combinesmulti-curve fittingwith multi-objective optimization，and improves objective function of impact load parameters identification based onmeasured impact load models structure.On thisbasis，ituses fastnon-dominated sorting genetic algorithm（NSGA2）to identify the parameters of themeasured data and obtains Pareto solutions.Studies show that themodeling strategy can effectively reflect the impact characteristics of shock load.Identification results andmeasured data can wellmatch and verify the feasibility of the identification algorithm.

modeling of impact load；multi-curve fitting；multi-objective optimization；parameter identification；nondominated sorting genetic algorithm（NSGA2）

TM71

A

1003-8930（2015）09-0080-05

10.3969/j.issn.1003-8930.2015.09.14

秦贞良（1990—），男，硕士研究生，研究方向为电力系统分析与负荷建模。Email：qinzhenl2007@126.com

2013-11-18；

2014-02-27

贾春娟（1969—），女，通信作者，博士，副教授，研究方向为电力系统分析、新能源发电。Email：jiachunjuan@sdu.edu.cn

张卫星（1958—），女，硕士，教授，研究方向为电力电子技术在电力系统应用。Email：zhweix@sdu.edu.cn