运用多分类多核参数SVM的变压器故障诊断算法

张庆磊，王宝华，陈祥睿（.南京理工大学自动化院，南京0094；.南京供电公司，南京0000）

运用多分类多核参数SVM的变压器故障诊断算法

张庆磊1，王宝华1，陈祥睿2
（1.南京理工大学自动化院，南京210094；2.南京供电公司，南京210000）

针对变压器故障诊断中支持向量机（SVM）的核参数选择和特征值权重问题，对多分类多核参数SVM算法做了改进。该方法研究了核参数对多分类SVM分类器分类性能的影响，采用多核参数表示输入特征分量的权重，通过最优化分类间隔来获得核参数的最优值，使SVM的分类性能达到最优。实验表明此算法拥有最优的分类性能，可以提高变压器诊断的精度和效率，拥有良好的应用前景。

多分类；多核参数；支持向量机（SVM）；变压器；故障诊断

变压器是电力系统重要设备，其运行状态直接影响电力系统的安全与稳定。变压器油中溶解气体分析DGA（dissolved gasanalysis）方法，由于其直观简单的特点，已得到了广泛研究和运用。但变压器结构复杂，故障原因多变，故障表现和故障原理之间存在模糊性和复杂性，使得故障诊断存在许多困难。近年来，大量智能算法被运用于变压器故障诊断中，而支持向量机算法SVM（support vectormachines）因为其训练样本数目要求小，诊断准确率高，鲁棒性好，得到了广泛的运用。但变压器故障诊断由于本身的一些特点和技术要求，传统的SVM难以获得理想的诊断效果。

变压器故障诊断属于多分类问题，并需要考虑多个特征量，想要获得较好的分类效果，则需要使用多个核参数。传统的多分类SVM方法如“一对一”和“一对多”[1]有着算法复杂、计算耗时久的缺点，而整体优化方法[2-3]在一个目标函数中同时考虑所有子分类器的优化参数，降低了优化算法的复杂程度，改善了SVM性能。文献[4-7]采用多个核函数，提出了多分类多核学习的SVM算法，在传统单核SVM基础上再增加了一层线性节点，将单核的分类结果线性叠加得到多核的运算结果。

在SVM的运用中，核参数的选择是一个关键。文献[8]采用高斯函数作为核函数，并定义同类的几何中心为该类的类中心，非同类的类中心之间的间距定义为类间距，研究了高斯核的宽对类间距的影响，并且证明了类间距全局收敛且存在极值，进而通过求极值点达到最优化核参数的目的。其他选择核参数的方法如考虑核相似性最大[9]、核空间聚类[10]等，都得到了研究和运用。DGA算法通常使用变压器油中H2、CH4、C2H2、C2H4、C2H65种溶解气体的含量作为样本输入特征量。若要得到性能更好的SVM分类器，则必须研究这些特征量对分类器性能的影响。文献[11]通过测量类间距来筛选样本输入的特征量，能够准确、快速地选择特征量并确定核参数。该文献仅去除了对影响分类性能无关或影响较小的特征量，没有考虑余下的有效特征量的权重问题。

针对这些问题，本文重新定义了多分类样本的类间距，采用高斯函数作为核函数，分析高斯核的宽度在类间距最优化过程中的作用，提出考虑核参数选择的优化方法。并且将高斯函数变形，把单核参数推广到考虑特征分量权重的多核参数分类方法，提出了基于多分类多核参数的支持向量机MMP_SVM（multiclassmultiple parameters supportvectormachine）方法。实验表明，该方法分类性能高于一般SVM，有较好的应用前景。

1 多分类SVM

1.1 凸外形二分SVM

令S为m个训练样本的合集，S=（{xi，y）i；i= 1，2，…，m}，，其中xi∈Rn。定义I1和I2为类1和类2的样本标签集合。若i∈I1，则yi=-1；若i∈I2，则yi=1。传统的二分SVM是找到最优超平面H= {x∈X：wTx-b=0}，将两类样本分开。在两类样本中，寻找一对穿过两类样本点的平行线，并通过最大化平行线的间隔来得到最优超平面，如图1（a）所示。上述问题可以表示为

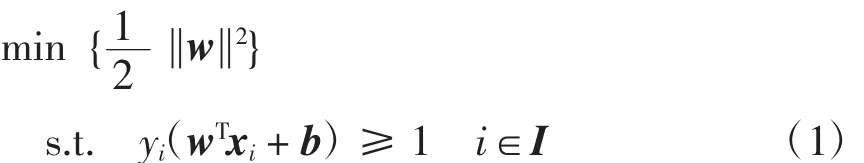
文献[12]指出，该最优化过程可以用另一种形式表示。定义P1和P2为各自两类样本点的线性组合的集合，代表类各自所在的凸多边形区域，如图1（b）所示。最优化问题就变为寻找v1∈P1和v2∈P2，使得‖v1-v‖22最小。最优化得到两点间隔就是类间距，两点的垂直平分线就是分类间隔，而分类面可以表示为

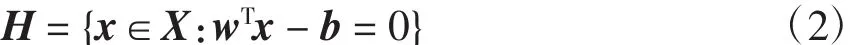
式中：w=v1-v2；b=（v1+v2）T（v1-v2）/2。v1和v2可以看作各自类中元素的线性组合。

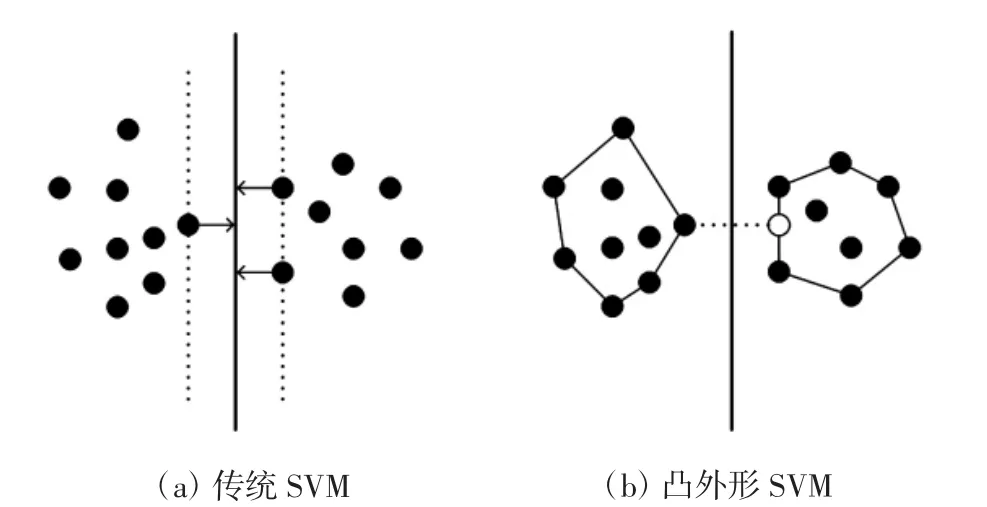
图1 SVM分类超平面的选取Fig.1 Classification hyperplane selected by SVM

则最优化过程可以表示为

分类器还可以用另一种方式表示。定义c=（v1+v2）/2，c为v1和v2的中点，若测试样本在I1中，则有

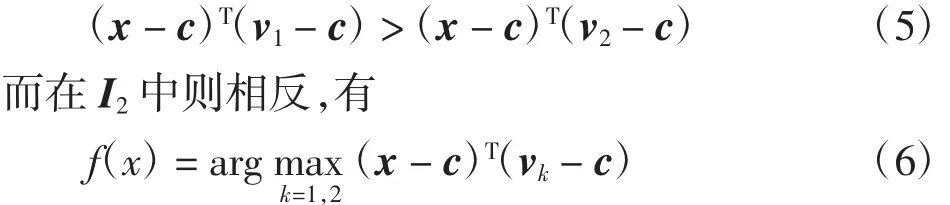
1.2 凸外形多分类SVM

二分SVM拓展到多分类，即有K个分类数目。定义训练样本集S={（xi，yi）；i=1，2，…，m}，xi∈Rn，yi∈{1，2，…，K}，则最优化的目标就成为最小化所有类凸多边形的间隔之和，即

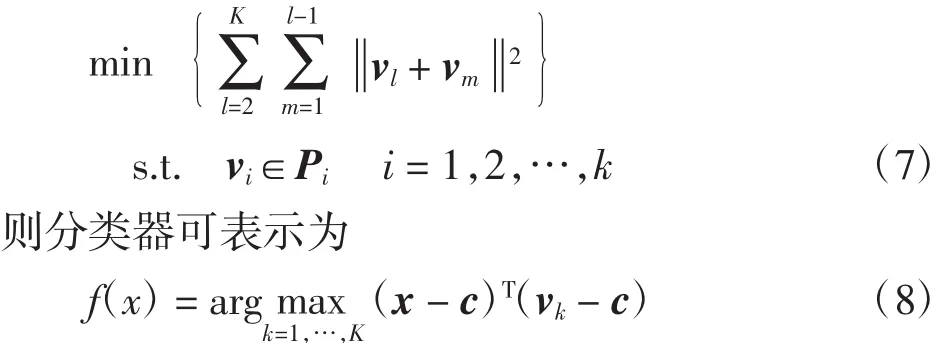
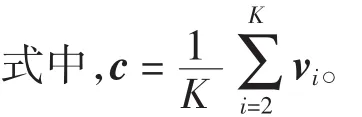
式（7）带入样本数据，可表示为

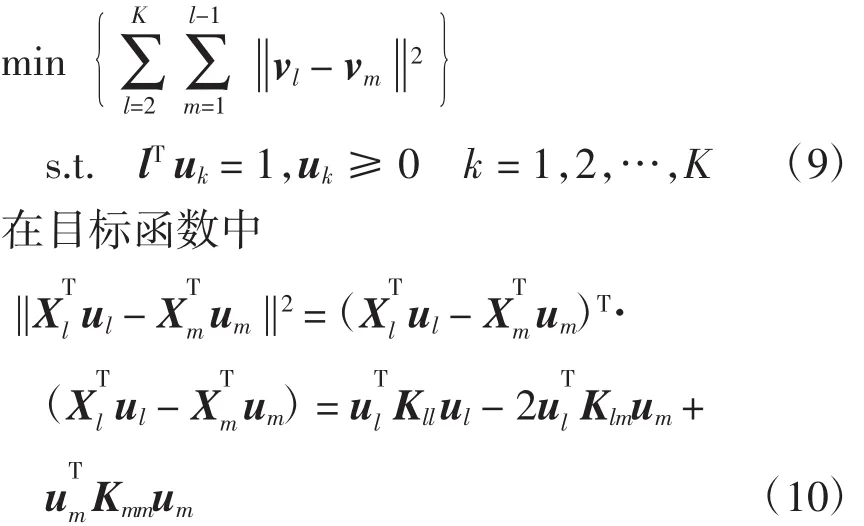
式中：Xl为由所有属于l类的样本x（ii∈I）l拼接成的矩阵；ul为对应的权值。

Kij=j表示属于类i和类j的所有样本之间的内积。

于是最优化过程可表示为

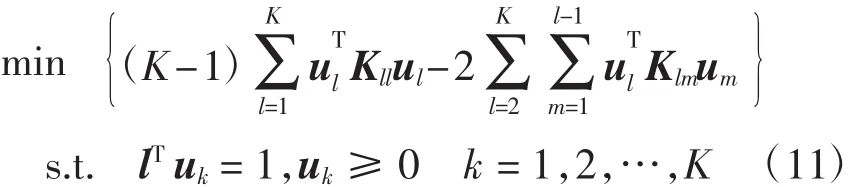
式（11）刚好对所有样本输入仅做一次内积（Kij与Kji是不同的两次内积，尽管他们的值是相同的）。建立一个m×m的矩阵α，α=（αi）j，且当样本i和样本j属于同一类时，αij=K-1；当样本i和样本j不属于同一类时，αij=-1。则式（11）的目标函数以内积形式可表示为

上述所有推导都是在原空间进行的，但在样本映射的Hilbert空间也同样适用，用核函数取代内积，最优化过程可表示为

同样，将内积以核函数代替，分类器最终可表示为

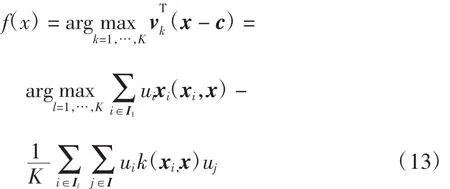
2 核参数的选择

2.1 核参数对分类性能的影响

采用高斯函数作为核函数，研究核参数λ∈[0，∞）的变化对分类器性能的影响。核函数为

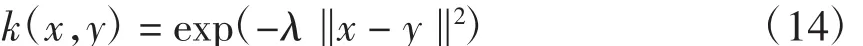
式（12）的目标函数的最小值W（u~），其物理意义表示在Hilbert空间中各类的类间距之和，那么类间距之和越大，样本的可分性就越好。找到λ∈[0，∞）使得类间距达到最大，那么此时的λ就可以认为是最优的核参数。

式（12）引入λ作为变量，即目标函数拥有2个最优化对象，表示为W（，λ）。

考察代价函数，即

设Dij表示xi和xj在Hilbert空间的映射φ（和φ（x）j之间的距离，则核函数表示为

当λ=0时，Dij=0，此时所有的样本输入都被映射到一点，所以样本映射的所有线性组合也是位于同一点，即有

从而退化为对角矩阵，此时对于所有属于Ij的样本i，对应的乘子都有

式中，W（λ）≥0且可导。根据拉格朗日中值定理，必存在ξ1∈（0，∞），使得）〉0

实际上，由于二次规划迭代精度有限，当λ= ξ2足够大时，ui就退化为式（20）的常数，此时

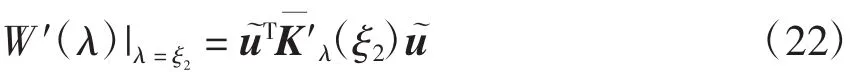
为了清楚地观察W（λ）和λ的关系，利用加州大学UCI网站下载的公开实测特征数据库Iris、Wine和Soybean对优化算法进行仿真验证，并分别绘制了λ-W（λ）曲线，如图2所示，横坐标采用对数坐标。从图中可以看出，W（λ）在λ=0为0，而在λ→∞时趋于某个正常数，这个常数和式计算的相吻合，并且W（λ）在某处存在极大值。设λ=λξ时W（λ）有极大值，那么λξ即为最优核参数。

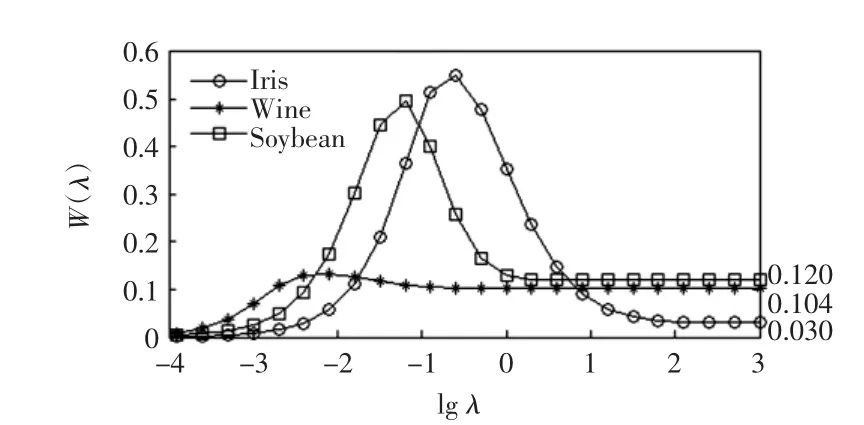
图2 三样本集的λ-W（λ）曲线Fig.2λ-W（λ）curves for 3 kindsof datasets

2.2 核参数的求解

若|λ1-λ0|≤η，则迭代结束（η是人为取的某一较小值，表示最优化结束条件）；若|λ1-λ0|〉η，则更新λ0，转步骤1。

步骤1使用二次规划求解最优值，同一般SVM最优化算法相同，步骤2使用最速下降法求解最优值。

在λ0=1、λ0=50条件下，通过步骤1求解u~= argmin u后，描绘了W（u~）关于λ的变化曲线，如图3所示。图中虚线的最大值对应的横坐标就是步骤2所要求解的λ1；对应的纵坐标表示λ= λ0条件下获得的最优间隔。每个λ0都对应一个最优解λ1和最优间隔W（λ）|λ=λ1。图3中实线表示最优间隔对于λ0的全局变化趋势。从图中可看出，实曲线拥有一个最大值，所在点的λ值就是全局最优点，即是最终要获得的理想核参数。在λ0=1和λ0=50情况下，最大值和全局最优点总是在初值的同一边，可以说步骤2的最优化过程总是趋向于最终目标的。

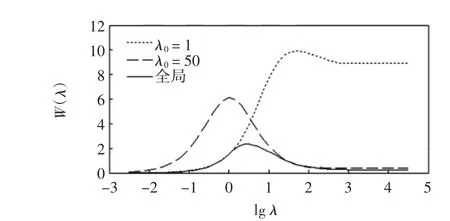
图3 已知λ0条件下的λ-W（λ）曲线Fig.3λ-W（λ）curvesw ith knownλ0

3 考虑输入特征分量的多核参数SVM

假设X和Z有S个特征分量，Xi与Zi是其中的第i个特征分量。

选取核函数为

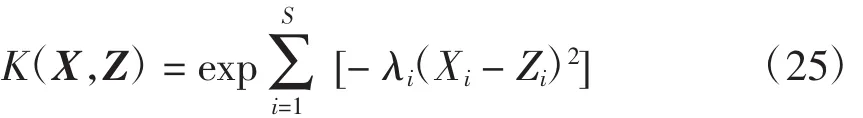
式中，λi一方面构成了高斯函数的宽，另一方面也包含特征量之间的权重关系。若某一个λ值较小，则表示该特征量对于分类结果的影响较小；若值较大，则表示分类结果对这一特征量更为敏感。

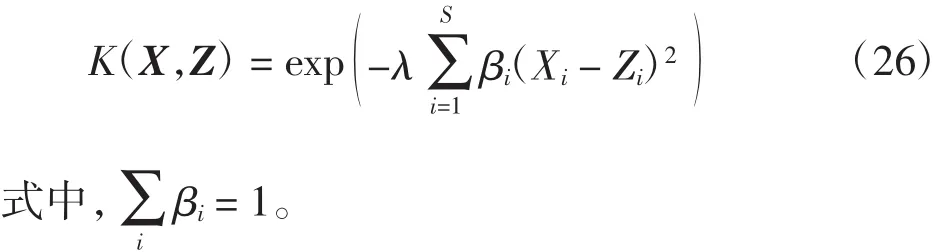
采用第2.2节中的两步迭代方法最优化多个核参数。但多维优化更加难以收敛，所以将核函数分解为赋初值βi=，n为样本特征量数目，通过两步迭代法求解λ，再通过约束条件下最优化方法来求解βi。

多分类多核参数SVM算法具体描述如下。

（1）定义样本集S=（{xi，y）i；i=1，2，…，m}，xi∈Rn，yi∈{1，2，…，K}。I={1，2，…，m}为样本标签集合，Ik⊂I表示属于k类样本的标签集合。

（2）选取核参数初值λ0=1，迭代次数s=0，设定结束条件η。

（3）令λ=λ0，s=s+1。选取核函数为

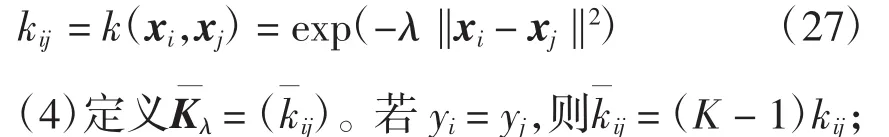
式中，ε0和τ均为用户选择的常数。若|λ0-λ1|≤η，继续下一步；反之，更新λ0，即λ0=λ1。转至步骤（3）。

（7）选取核函数为

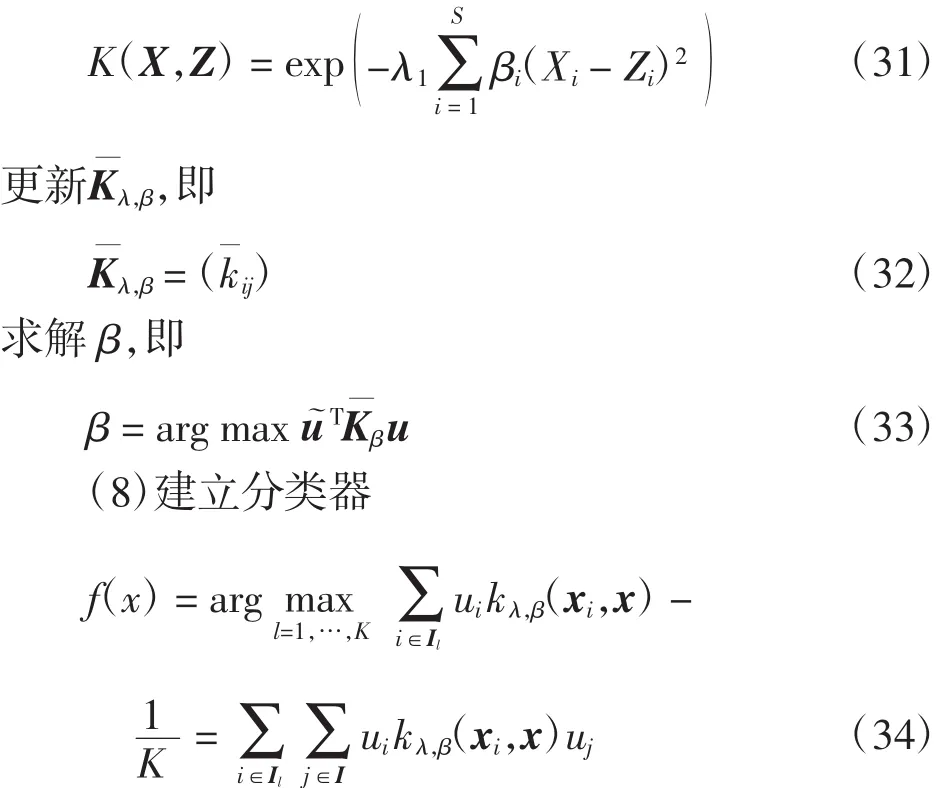
4 诊断实例

搜集确定实际故障结果的84组变压器油中气体分析检测记录，其中28组作为训练样本，其余作为测试样本。选择变压器油中H2、CH4、C2H2、C2H4、C2H6这5种溶解气体的含量作为样本输入特征量，输入量为xi=（xi1，xi2，xi3，xi4，xi5）T，溶解气体含量差异较大，为提高诊断精度，对DGA数据做归一化处理，即

考虑以下6种故障模式：低温过热T1、中温过热T2、高温过热T3、局部放电（PD）、低能放电D1和高能放电D2。使用三比值法、BP神经网络（back prop-agation network）、一对多（one-versus-all，OVA）SVM和MMP_SVM模型对相同的样本进行比较实验。各方法的训练时间、训练经验误差、测试准确率如表1所示。表2列举了样本集的5种典型样本的诊断实例。

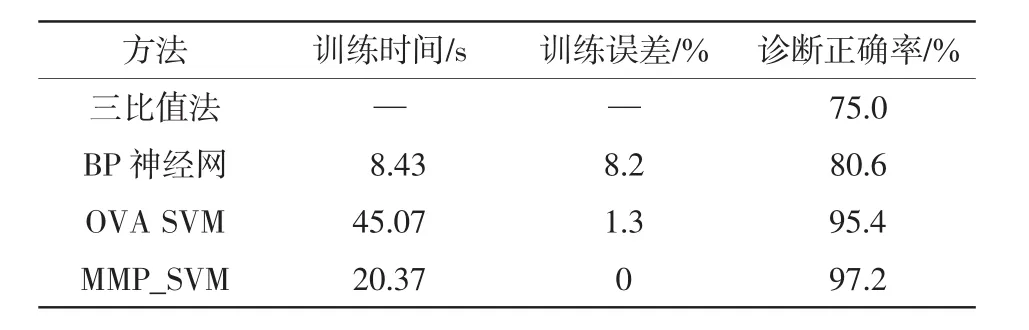
表1 不同方法的诊断结果比较Tab.1 Comparison of faultdiagnosis resultsvia different methods

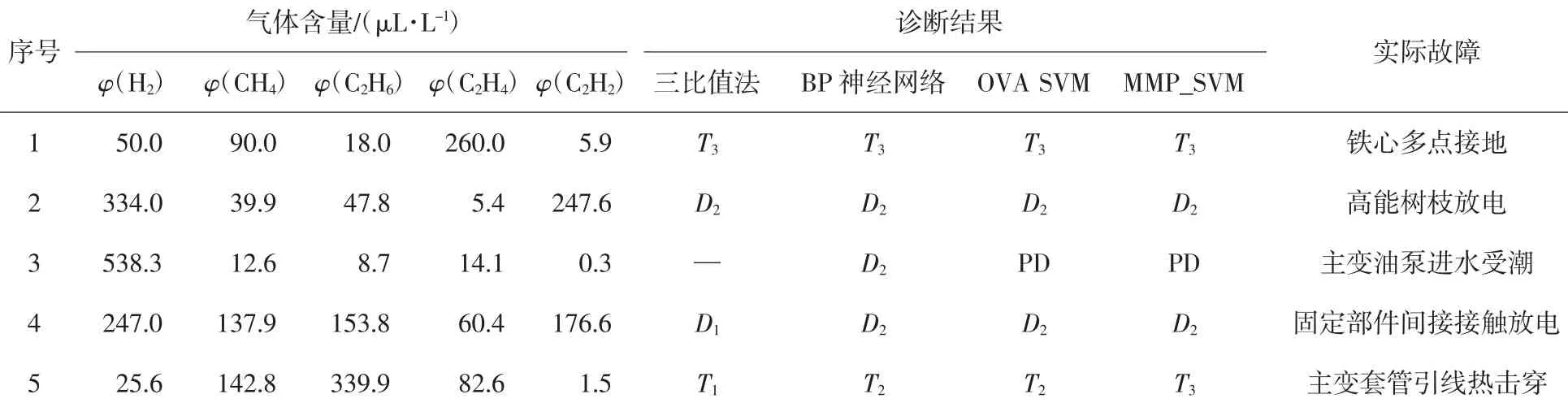
表2 变压器故障诊断实例Tab.2 PracticalexaMplesof fault diagnosis for power transformer

实验数据表明：

（1）在小样本的情况下MMP_SVM算法仍然具有很好的泛化能力，诊断结果与实际诊断结果吻合得很好。相比样本训练数目要求较多的BP神经网络，该算法拥有更高的诊断准确率。

（2）MMP_SVM准确率比OVA SVM稍高，但训练时间却大大减少。因为该算法最优化过程中需要求解的参数少，且同时计算最优化核参数；而OVA SVM必须重复计算多个分类机，并且通过交叉验证法最优化核参数，另在诊断实验中，OVA SVM仅考虑单一核参数的选择，训练时间是MMP_SVM的2倍。

5 结论

本文提出了基于凸外形的多分类、面向特征值权重的多核参数向量机模型，并将其运用于变压器故障诊断。该模型具有如下优点。

（1）相比于传统的SVM模型，该模型避免了中间运算，从输入数据直接获得输出分类结果，且运算过程清晰、简单，有效地避免混淆和差错的可能性。

（2）选择合适的核参数来考虑特征值的权值，样本的不均衡性不会对分类精度产生太大影响，进一步加强模型的分类能力。核参数的选择可以用单一的数学式表达，核参数的数量不再显著地影响运算复杂程度。

（3）将模型分解为1个凸规划问题和2个约束最优化问题，降低问题复杂度，加快了收敛速度。

实验表明，该模型能保证较高的诊断准确性，有着良好的运用前景。

[1]Hsu Chih-Wei，Lin Chih-Jen．A comparison ofmethods for multiclasssupportvectormachines[J]．IEEETranson Neural Networks，2002，13（2）：415-425．

[2]Crammer K，Singer Y.On the algorithmic implementation ofmulticlass kernel-based vectormachines[J].Journal of Machine Learning Research，2002，2（2）：265-292.

[3]Crammer K，Singer Y．On the learnability and design of outputcodes formulticlassproblems[J]．Machine Learning，2002，47（2/3）：201-233.

[4]郭创新，朱乘治，张琳，等（Guo Chuangxin，Zhu Chengzhi，Zhang Lin，etal）．应用多分类多核学习支持向量机的变压器故障诊断方法（A fault diagnosis method for power transformer based onmulticlassmultiple-kernel learning support vectormachine）[J]．中国电机工程学报（Proceedingsof the CSEE），2010，30（13）：128-134．

[5]KiMSeung-Jean，Magnani A，Boyd S．Optimal kernel selection in kernel fisher discriminantanalysis[C]//23rd InternationalConference on Machine Learning.Pitts-burgh，USA，2006：465-472．

[6]朱苏航，吕干云（Zhu Suhang，LüGanyun）．利用遗传支持向量机进行电压暂降信号识别（Voltage sag signal identificationwith GA-SVM）[J]．电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2012，24（1）：84-87．

[7]Lee Y，Wahba G，Ackerman SA.Cloud classification of satellite radiancedatabymulticategory supportvectormachines[J].Journal of Atmospheric and Oceanic Technology，2004，21（2）：159-169．

[8]宋小衫，蒋晓瑜，罗建华，等（Song Xiaoshan，Jiang Xiaoyu，Luo Jianhua，etal）．基于类间距的径向基函数-支持向量机核参数评价方法分析（Analysis of the inter-class distance-based kernel parameter evaluating method for RBF-SVM）[J]．兵工学报（Acta Armamentarii），2012，33（2）：203-208．

[9]唐耀华，郭为民，高静怀（Tang Yaohua，GuoWeimin，Gao Jinghuai）．基于核相似性差异最大化的支持向量机参数选择算法（SVMparameter selection algorithMbased onmaximuMkernel similarity diversity）[J]．模式识别与人工智能（PR&AI），2010，23（2）：210-215．

[10]刘琼荪，范瑞雅（Liu Qiongsun，Fan Ruiya）．确定高斯核参数的聚类方法（Method ofdetermining Gaussian kernel parameter by clustering）[J]．计算机工程与应用（Computer Engineering and Applications），2011，47（3）：38-40，60.

[11]黄应清，赵锴，蒋晓瑜（Huang Yingqing，Zhao Kai，Jiang Xiaoyu）．基于核空间类间平均距的径向基函数—支持向量机特征选择算法（RBF-SVMfeature selection arithmetic based on kernelspacemean inter-class distance）[J]．计算机应用研究（Application Research of Computers），2012，29（12）：4556-4559．

[12]Nanculef R，Concha C，Allende H，etal.A lightextension of SVMs for multicategory classification[J].International Journal of Hybrid Intelligent Systems，2009，6（2）：69-79.

Research of Transformer Fault Diagnosis Based on MulticlassMultiple ParametersSVM

ZHANGQinglei1，WANGBaohua1，CHENXiangrui2
（1.College of Automation，Nanjing University of Science and Technology，Nanjing 210094，China；2.Jiangsu Electric Power Company，Nanjing210000，China）

In order to tackle the problems of support vector machines（SVM）parameters selection and feature′s contribution for the application of transformer fault diagnosis，multiclass multiple parameters support vector machine（MMP_SVM）is improved in this paper.The effectof radial basis function（RBF）kernelparameterson the classification performance ofmulticlass SVMis analyzed，and every features′contribution is considered to obtain the bestperformance of SVM，this is carried outby tuningmultiple kernel parameters automatically through optimizing the interclass distance.The results of experiments indicate that the algorithMof this paper demonstrates the best performance and has high classification accuracy when applied for transformer fault diagnosis，which proves its effectiveness and usefulness.

multiclass；multiple parameters；supportvectormachine（SVM）；transformer；faultdiagnosis

TM855

A

1003-8930（2015）09-0097-06

10.3969/j.issn.1003-8930.2015.09.17

张庆磊（1989—），男，硕士研究生，研究方向为智能控制理论及其在电力系统中的运用。Email：czxqzql@126.com

2013-10-09；

2014-04-14

王宝华（1968—），男，博士，副教授，研究方向为电力系统分析、运行、控制与规划。Email：13951845674@163.com

陈祥睿（1988—），男，硕士研究生，研究方向为电力系统。Email：291824318@qq.com