NICA算法在多类型分布式电源规划中的应用

王进，陈加飞，刘娇，许一帆，杨芳华，唐浩（.长沙理工大学电气与信息工程学院，长沙404；.湖南省怀化市沅陵县辰州东街凤滩水力发电厂，怀化49699）

NICA算法在多类型分布式电源规划中的应用

王进1，陈加飞1，刘娇1，许一帆1，杨芳华1，唐浩2
（1.长沙理工大学电气与信息工程学院，长沙410114；2.湖南省怀化市沅陵县辰州东街凤滩水力发电厂，怀化419699）

在综合多种分布式电源出力与负荷时序特性的基础上，建立了兼顾环境因素、发电成本、网损和静态电压稳定裕度的分布式电源多目标规划模型；提出了应用一种新的免疫克隆算法NICA（novel immune clonal algorithm）来求解该模型。该算法采用整体克隆非支配抗体、非一致性变异和删除帕累托（Pareto）前端密集解的策略来保证算法的收敛速度和解的均匀性。以IEEE33节点配电测试系统为例，与改进非劣分层遗传算法NSGA-II（non-dominated sorting genetic algorithMII）相比，算例分析结果表明，该算法所得最优解在Pareto-前端的分布更宽广、更均匀，验证了该算法的可行性和有效性。

分布式电源；时序特性；多目标规划；新的免疫克隆算法；帕累托前端

近年来，由于能源和环境问题，分布式电源DG（distributed generation）得到迅速发展，在电力行业得到越来越多关注[1]。当大量的DG接入配电网时，将对系统带来很大的影响，其影响程度与DG安装位置和容量密切相关[2]。

DG规划一般包括选定安装位置和确定安装容量，以及综合考虑两者之间的协调关系[3]。随着电力系统规模的不断扩大，接入DG的种类日益增多。不同类型DG的出力特性不同，其对电网的影响程度不同，因此，有必要对DG类型进行合理的选择。DG的种类主要包括微型燃气轮机、风力发电、太阳能发电、储能电池、小水电等。由于风电、光伏等DG的出力并不恒定，为了使规划结果更接近实际，应考虑DG和负荷的时序特性[4]。

随着电力系统规模的不断扩大，对DG的规划研究从单目标[5-6]逐渐发展为考虑多个目标的规划问题。国内外学者对分布式电源的多目标规划进行了一些研究。文献[7]考虑了有功网损、电压改善程度和环境改善程度3个指标，并将其转化为一个多目标非线性规划问题来求解，对多目标的求解算法，实质是通过加权将多目标转化为单目标问题进行求解；文献[8]建立了投资成本最小、配电网网损最小和静态电压稳定性最大的多目标优化配置模型，并应用基于小生境技术的多目标遗传算法来求解，但并没有考虑Pareto解在Pareto-前端上的均匀性和多样性。

免疫克隆算法是基于人工免疫系统的进化算法，它具有很高的搜索效率和寻优能力，在工程中得到广泛应用[9-10]。在此基础上，提出了一种新的免疫克隆算法NICA（novel immune clonal algorithm）来求解多目标问题，其很强的全局搜索能力、较强的收敛能力以及很好地保持多样性的能力在多个测试问题上都优于NSGA-II等经典多目标算法[11]。

本文在不考虑负荷新增节点的情况下，以风电、光伏发电、微型燃气轮机和储能电池为研究对象，建立考虑环境因素和时序特性的DG发电成本最小、网络损耗最小、静态电压稳定裕度最大的分布式电源多目标规划模型，并应用NICA算法对规划模型进行求解；最后与经典的多目标算法NSGA-II进行了比较分析。

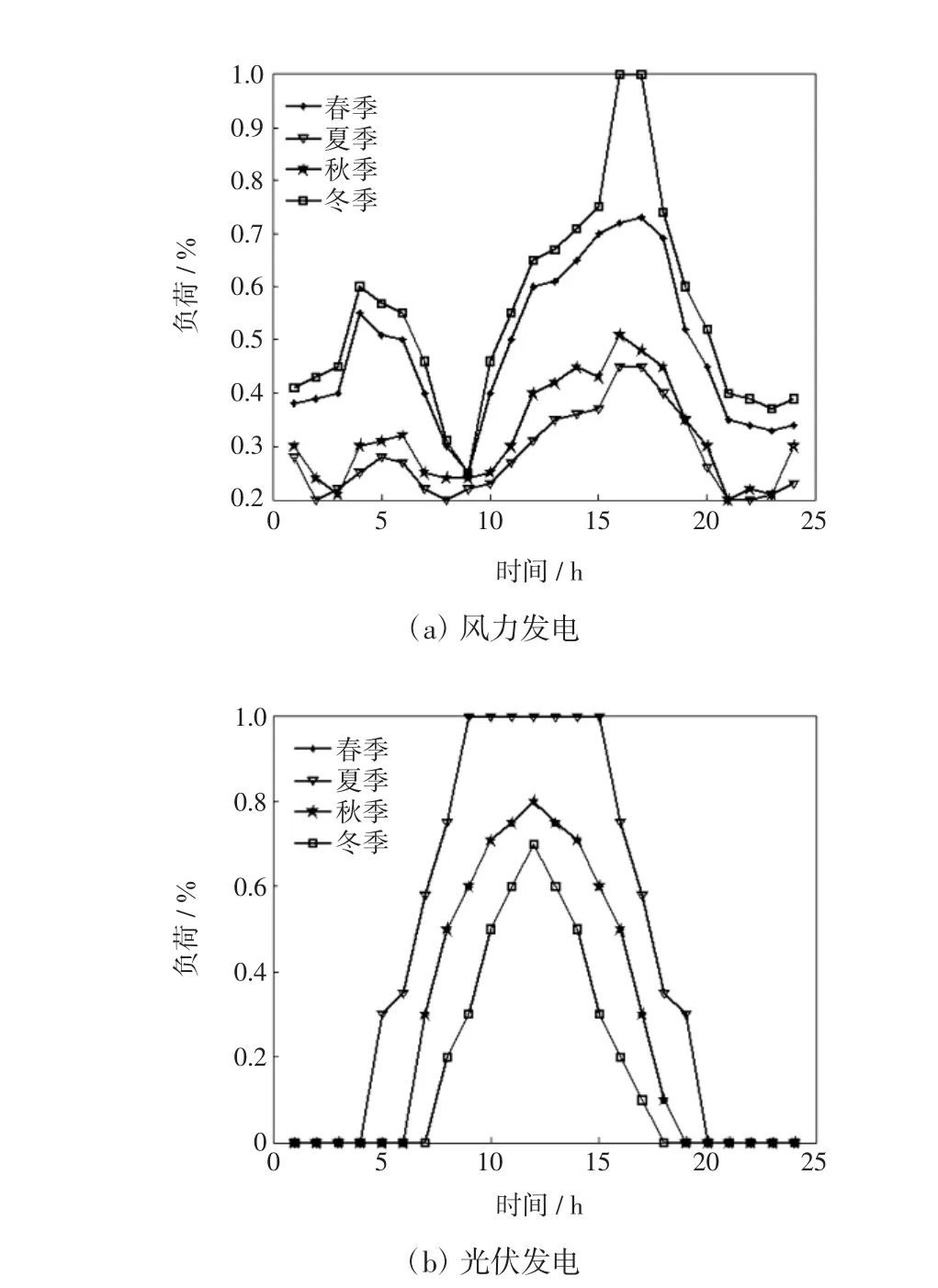
图1 DG出力时序特性曲线Fig.1 TiMing characteristic curvesof DG daily output

1 DG出力和负荷的时序特性

1.1 DG出力时序特性

不同于传统电源，风力发电和光伏发电受环境影响较大，其出力大小随着地理位置和气候环境的变化而变化，且在相同地区的不同季节变化也会不同。虽然风能和光照强度有较大的随机性，但其本身具有统计规律[12]。可根据气象资料统计出规划地区的风能和光照强度在时序上的变化规律，从而计算出风力发电和光伏发电的出力时序特性，如图1所示。

1.2 负荷时序特性

根据行业的不同，可将负荷分为重工业、轻工业、商业、市政和居民5种典型负荷，在规划地区负荷预测的基础上，可得出不同负荷在不同季节的时序特性[13]。本文以商业、市政和居民负荷为研究对象，其时序特性如图2所示。

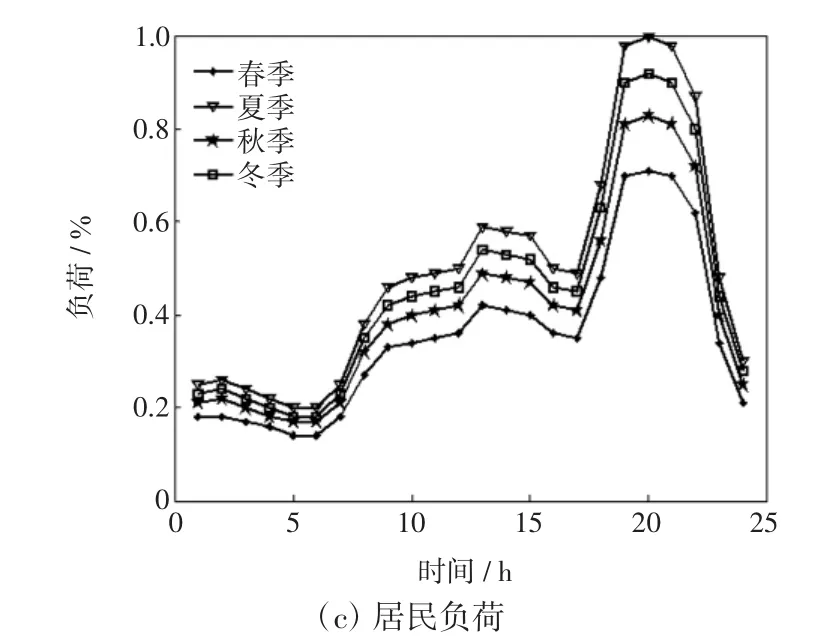
图2 负荷时序特性曲线Fig.2 TiMing characteristic curvesof three curves loads

2 考虑DG出力与负荷时序特性的DG多目标规划模型

配电网规划的目的是既能可靠安全地运行也能使经济达到最优，所以目标函数应既要包括静态电压稳定裕度和系统负荷节点电压偏移量等技术性指标，也要包括DG投资成本、运行成本、燃料成本和有功网损等经济指标。针对这两个方面，以微型燃气轮机、风力发电、光伏发电及储能电池为候选类型，在DG类型和容量都不确定的情况下，建立了包括考虑环境因素的DG发电成本、有功网损和静态电压稳定裕度的多目标规划模型。本文将储能电池与风力发电和光伏发电结合，实现调峰作用[14-15]，即储能电池在负荷较低的时间段充电，在负荷较高的时间段放电。

2.1 考虑环境因素的DG发电成本

本文以多种分布式电源的投资安装成本、设备一年（8 760 h）的维护成本和微型燃汽轮机一年的燃料成本及环境成本为目标函数，即

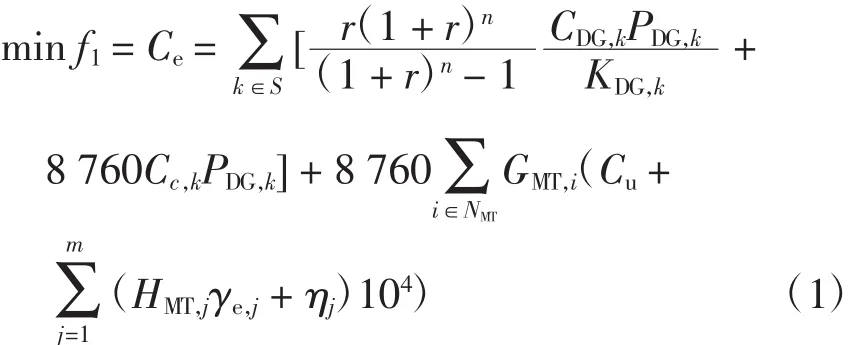
式中：Ce为考虑环境因素的DG发电成本；S为DG的种类集合；r为折现率，取10%；n为设备使用年限，取25 a；PDG，k、CDG，k和KDG，k分别为第k种DG接入的容量、安装投资成本和平均容量系数；Cc，k为第k种DG的维护成本；NMT为微型燃气轮机的待选节点集合；GMT，i为第i节点处微型燃气轮机每小时的出力；Cu为微型燃气轮机每小时燃料费用；m为微型燃气轮机排放气体污染物的种类，此处考虑CO2和NOx两类；HMT，j和γe，j分别为第j种气体的排放强度及环境价值；ηj为排放第j种气体所受罚款。

表1为微型燃气轮机排放CO2和NOx的相关参数。

表1 污染气体相关参数Tab.1 Parametersof pollutanteMission

2.2 考虑网络损耗的目标函数

以系统一年平均每小时的网络损耗为目标函数，即

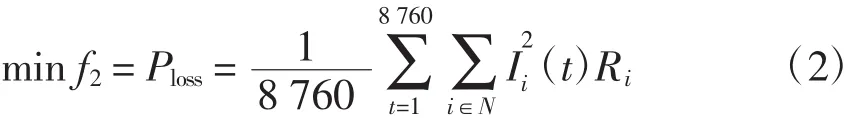
式中：Ploss为系统一年平均每小时的网损；N为节点集合；Ii（t）为第i条支路在t时刻的电流；Ri为第i条支路的电阻。

2.3 静态电压稳定裕度

电压稳定性指标为

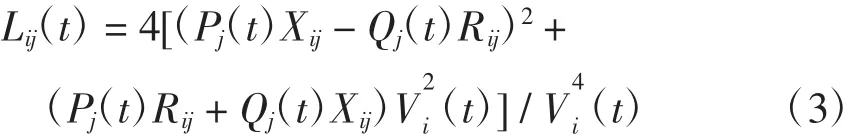
式中：Lij（t）为支路ij（首节点为i末节点为j）t时刻的电压稳定指标；Pj（t）和Qj（t）分别为流入支路末端节点j在t时刻的有功及无功功率；Rij和Xij分别为支路ij的电阻和电抗；Vi（t）为首端节点i在t时刻的电压。

整个配电系统的静态电压稳定指标L（t）定义为所有支路在时刻t的静态电压稳定指标中的最大者，即

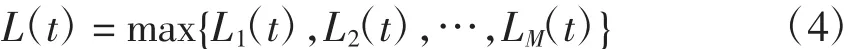
式中，M为系统总支路数。则配电网在t时刻的电压稳定裕度为

则电压稳定指标L（t）越小，静态电压稳定裕度K（t）越大。本文以一年平均每小时的静态电压稳定指标为目标函数，即

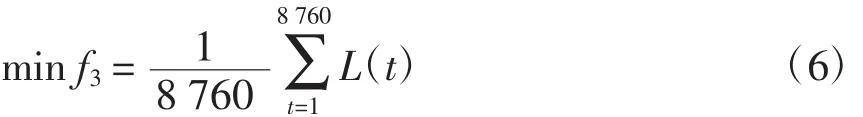
约束条件包括等式约束和不等式约束，其中，等式约束为节点潮流方程，即

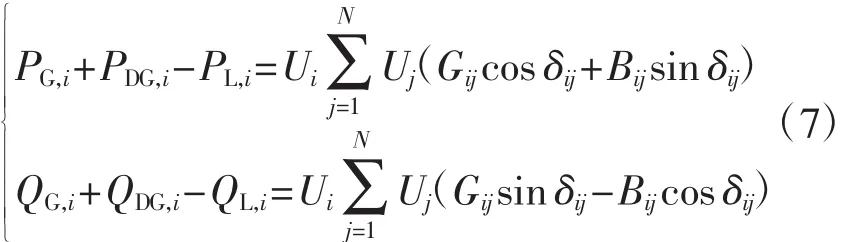
式中，P为i节点处接入的DG容量；Pmax为节

DG，iDG，i点i处的允许接入的最大DG容量。（2）节点电压约束为

式中，Ui，max和Ui，min分别为节点i电压的上下限。

（3）支路潮流约束为

式中：NB为线路集合；Si，max为第i条线路的容量极限。

（4）节点注入DG的容量约束为

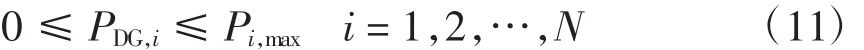
式中，Pi，max为第i组DG容量上限。

（5）储能电池的安装容量约束[16]为

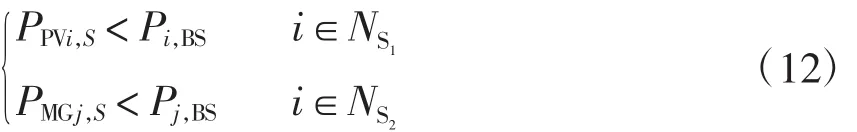
式中：NS1为接入光伏电源节点集合；NS2为接入风电源节点集合；Pi，BS为节点处储能电池安装容量；PPVi，S为节点i处光伏电源安装容量；PMGj，S为节点j处风电源安装容量；Pj，BS为节点j处储能电池安装容量。

而不等式约束包括5种，分别为（1）DG容量约束为

3 NICA算法在多类型分布式电源规划中的应用

3.1 NICA算法

3.1.1 整体克隆

不同于单目标，多目标的解之间是不能简单进行相互比较，这些解无法在改进任何目标函数的同时不削弱任何一个其他目标函数。所以，NICA并没有采用根据每个抗体的适应度函数来克隆的方式，而是采用整体克隆的方式，即对每个抗体采用相同的克隆比例。克隆操作实现了空间的扩张，为新的抗体种群和算法实现全局搜索提供了基础，有利于得到分布较广的Pareto前端。同时，促进抗体间的信息交流，有利于增加种群多样性，提高算法的收敛速度。

设初始抗体群A（it）为

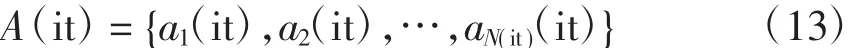
按整体克隆的策略，对A（it）施行克隆操作后得到抗体群A′（it）为

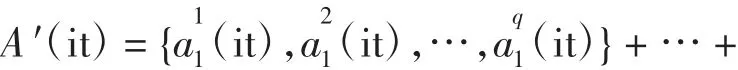
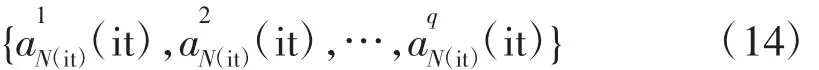
式中：q为克隆比例，it为当前迭代次数。

3.1.2 非一致性变异

免疫学认为，亲和度成熟和抗体多样性的产生主要依靠抗体的高频变异，而并非交叉和重组。因此，NICA只采用克隆变异而没有采用克隆重组。NICA算法使用的变异方式是非一致性变异，其操作如下。

假设抗体群A（′it）中的a（iit）为

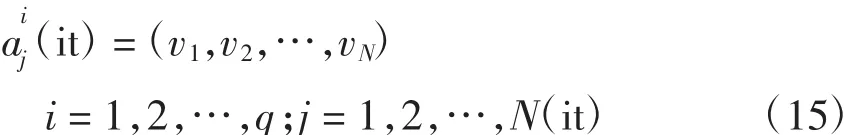
选取分量vk进行变异，其定义区间为[ak，bk]，则变异后的解为

水轮发电机组导水机构的传动机构中，往往需要将导叶臂和连接板相连，这时就需要通过剪断销的连接作用。剪断销保护装置由剪断销和信号器组成，导叶在正常运行过程中，剪断销带动导叶转动。一旦导叶中有异物卡住，导叶轴和导叶臂就会停止转动，但是连接板在叉头仍然带动其转动，并对剪断销进行剪切。若想剪断销被迅速剪断，需要进剪切力加至正常情况的1.5倍，使导叶脱离控制环，另外导叶仍可正常转动，有效防止了事故扩大。剪断剪断销后，剪断销信号器动合触点闭合，发出信号提醒相关操作人员。

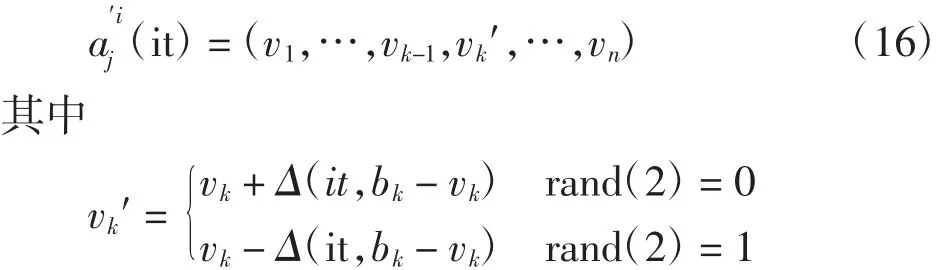
式中：rand（2）=0表示将随机均匀地产生的正整模2产生的结果；函数Δ（it，y）的值域为[0，y]，当it增大时，使得Δ（it，y）接近于0的概率增加。函数Δ（it，y）的表达为

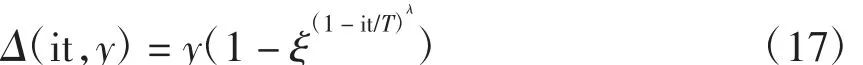
式中：ξ为[0，1]上的一个随机数；T为最大代数；λ为决定非一致性变异程度的参数，本文算法中取为2。

则变异后得到抗体群A″（it）为

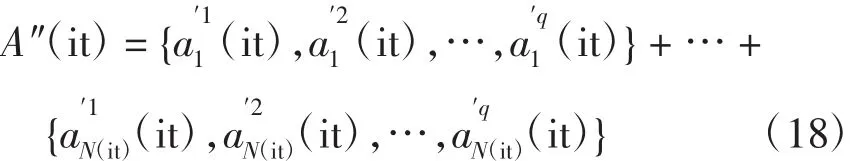
3.1.3 非支配抗体的选择

在NICA算法中，在施行克隆选择之前，首先要将抗体群A″（it）中的抗体划分为支配抗体群和非支配抗体群，其中非支配抗体群被选择到下一代。对任意一个抗体a*（it）∈A″（it），若a*（it）为当前代数中的非支配抗体，则必须满足的条件为

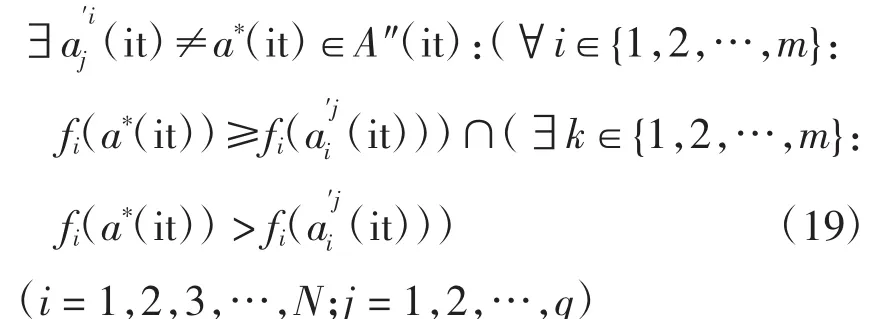
对抗体群A″（it）实现克隆选择操作，得到的非支配抗体群A‴（it）为

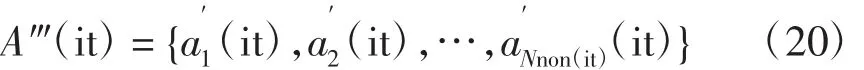
3.1.4 抗体群更新

根据NICA的选择策略，非支配抗体都应选择到下一代，由于采用的是整体克隆的方式，克隆后的规模很大，使运算速度变慢。因此，NICA采用抗体群更新策略，即当非支配抗体超过一定的数目Nn时，删除Pareto前端较密集的地方对应的抗体，从而保证算法的运算速度和Pareto解在Pareto前端分布的均匀性。其具体操作如下。

步骤2为抗体分配适应度。根据每个目标函数值将抗体群按升序排列。对边界解上的抗体，即最大和最小函数值的抗体，分配一个无穷大的适应度值。对其他抗体分配的适应度值为

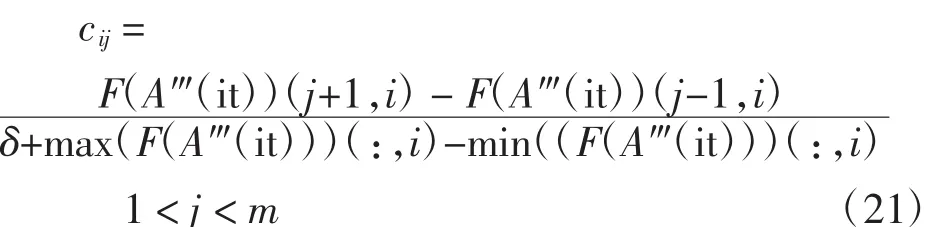
式中：max（F（A‴（it）））（：，i）和min（F（A‴（it）））分别为在抗体的目标值中第i个目标的最大值和最小值；δ为较小的正数，δ的作用是保证当max（F（A‴（it）））（：，i）=min（F（A‴（it）））（：，i）时，cij的分母不为0；F（A‴（it））（j+1，i）为抗体a′j+1（it）的第i个目标函数值。

步骤3计算第（j j=1，2，…，Nno（nit））个抗体的适应度函数值，即

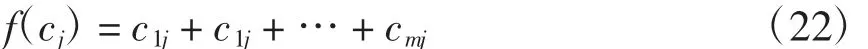
步骤4若非支配抗体数大于期望保留的抗体群规模Nn，删除适应度函数值最小的抗体，得到新的抗体群和目标函数矩阵；返回步骤2，直到非支配抗体的数目小于等于抗体群规模Nn。

实施抗体更新操作后得到抗体群A″（″it）为

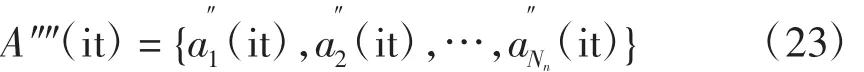
3.2 基于NICA的多类型DG规划

本文采用整数编码的方式，令PDG，i=xiPs，则xi取区间[0，PDGmaxi/Ps]内的实数值，其中，Ps为基准容量，PDGmaxi为节点i允许接入DG最大功率。1个抗体表示1种安装方案，分别取xMT，i、xWG，i、xPV，i和xBS，i表示4种DG的安装情况，即抗体可表示为

式中：m1为微型燃气轮机候选节点数；m2为风力发电候选节点数；m3为光伏发电的候选节点数；m4为储能电池候选节点数。xi为0表示该候选节点不接入DG；xi不为0则表示负荷节点上接入DG，且其安装容量为xiPs。

应用NICA对配电网中DG优化规划的流程如图3所示，步骤如下。

步骤1初始化。确定算法的参数，即抗体群规模N、最大迭代次数gmax、期望保留非支配抗体规模Nn、克隆比例R和变异概率Pm；输入配电网原始数据，对DG容量进行编码，根据各类DG接入容量约束条件生成初始抗体群。

步骤2根据克隆比例R和变异概率Pm对抗体群进行免疫克隆和非一致性变异操作，并根据抗体群的容量方案应用前推回代进行潮流计算和目标函数计算，根据目标函数值进行克隆选择操作，即选出非支配抗体。

步骤3根据期望保留非支配抗体群规模Nn对非支配抗体群进行抗体群更新操作，即删除Pareto前端中较密集的解。

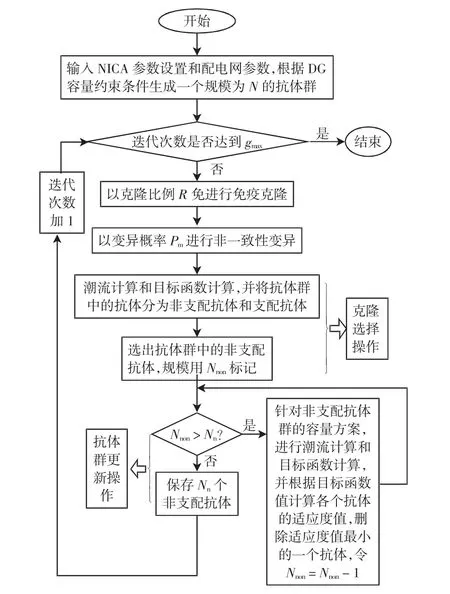
图3 基于NICA的DG多目标规划流程Fig.3 Flow chartof DGmulti-objective planning based on NICA

步骤4当迭代次数达到gmax时，计算结束；否则，重复步骤2和步骤3。

4 算例分析

4.1 算例描述

本文以图4所示的IEEE 33节点配电网系统为例，分别对微型燃气轮机、光伏发电、风力发电和储能电池的位置和容量进行优化规划。根据规划地区的自然条件和地理位置选择各类型的DG的安装候选位置：微型燃气轮机候选节点为2、5、7、12、16；光伏发电候选节点为6、13、17；风力发电候选节点为28、29、30、31；储能电池候选节点为6、13、17、28、29、30、31。同时，可获得该地区各负荷点的负荷类型：居民负荷节点为1、2、3、4、5、8、9、10、11、12、25、26、27、28、30、31、32；商业负荷节点为13、14、15、16、17、18、23、24、29；市政负荷节点为6、7、19、20、21、22。

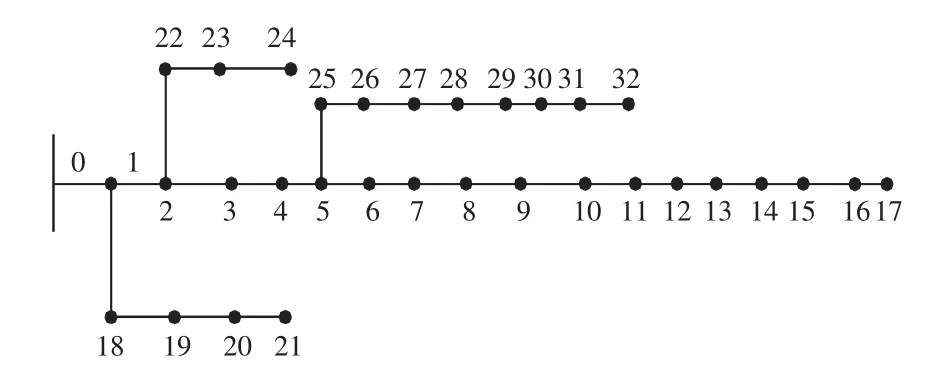
图4 IEEE33节点配电网Fig.4 lEEE33-bus distribution system

该系统电压等级为12.66 kV，配电网未接入DG前的有功负荷为3 715.0 kW，无功负荷为2 300.0 kvar。假设DG的功率因数为0.9，额定有功功率为0.1MW，则各类型DG的相关参数如表2所示。NICA算法的参数选取如下：克隆规模N为100，克隆比例R为4，变异概率Pm为0.33，算法迭代次数gmax为150。

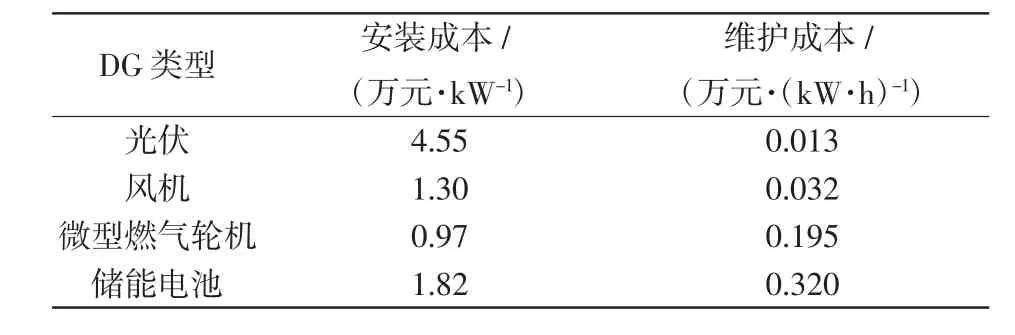
表2 DG参数Tab.2 Parametersof DG

4.2 算例结果

分别应用NSGA-II和NICA算法对DG进行规划，表3给出了2种算法得到的不同目标函数值的变化范围。

应用2种算法求解DG规划模型得到的Pareto-解空间分布如图5所示。

表3 2种算法得到的目标函数值的变化范围Tab.3 Rangsofobjective function value based on two algorithms

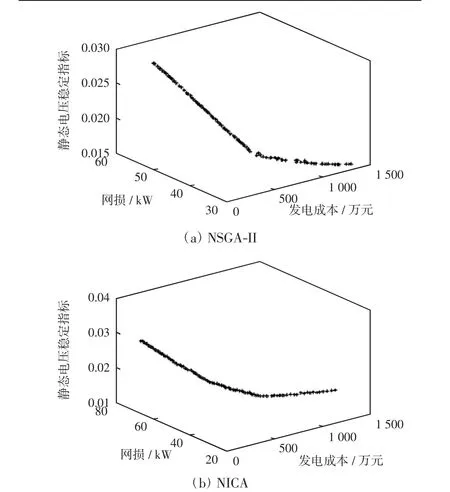
图5 2种算法的Pareto-解空间分布Fig.5 Distribution of Pareto-solution for two algorithMs

应用NICA算法对多类型DG优化规划的几种方案的比较如表4所示。

4.3 分析讨论

由表3可以看出，NICA所得的范围都大于NSGA-II所得的范围，说明NICA所得的解比NSGA-II所得解分布更为宽广。由图5可以看出，NSGA-II所得解在Pareto-前端上的分布出现了间断，而NICA所得解的分布较为均匀，表明NICA比NSGA-II所得的解在Pareto前端上更能保持良好的均匀性和多样性；同时可以看出NICA所得解的分布曲线比NSGA-II所得解的分布曲线平滑，表明NICA比NSGA-II更能协调好各个目标函数之间的相关性。

在表4中NICA对DG优化的几种规划方案中，方案1、2、3是3个代表性的配置方案，方案1是考虑环境因素的发电成本最小，规划结果为0，即不接入DG时，发电成本最小，但是网损和静态电压稳定指标的值较大；方案2是网损最小，方案3是静态电压稳定指标最小，由规划结果可以看出方案2和方案3的网损和电压稳定指标都较低，但是投资成本较大；方案4是采用折中法选择的无偏最优的配置方案，即投资成本、网损、电压稳定指标都较适中。此外，决策者可根据实际情况在Pareto-最优解集中选择符合实际要求的DG规划方案。

NICA采用整体克隆非支配抗体和删除Pareto-前端密集解的方式，既保证了算法的收敛性，又保证了Pareto-最优解在Pareto-前端上的均匀性和宽广性，以及对各个目标函数之间的协调性，使决策者的选择范围更大。

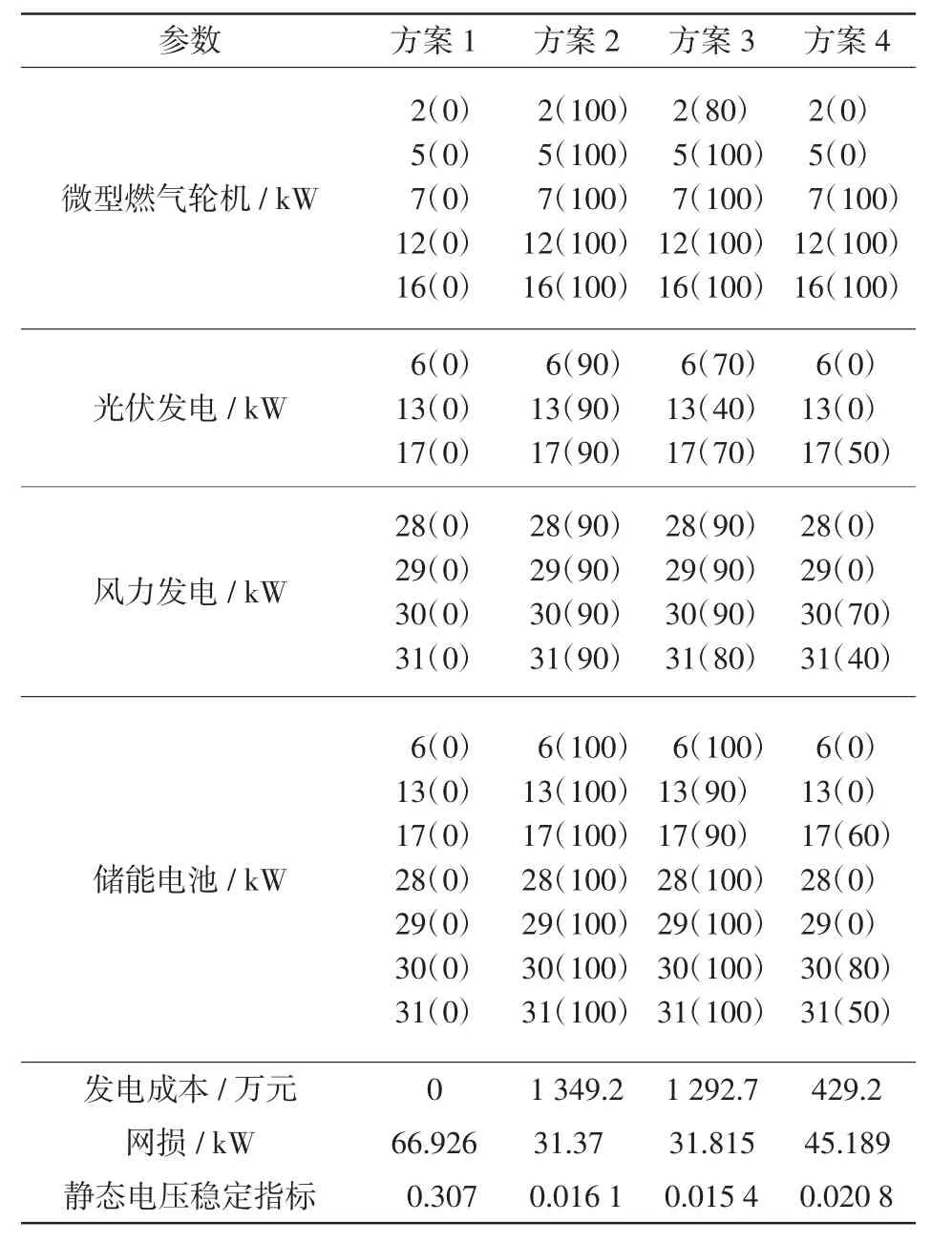
表4 DG规划方案比较Tab.4 CoMparison of DG deployment schemes

5 结语

对于含多种DG的配电网规划，本文针对DG出力的不稳定性，分析了分布式电源和负荷的时序特性，建立考虑环境因素的含多种DG配电网的多目标规划模型，使得规划方案更接近实际。应用NICA对DG多目标规划模型进行求解，通过仿真实验与NSGA-II进行比较，表明NICA得到的Pareto-解在Pareto-前端上收敛性、均匀性和宽广性更好，该算法在多类型分布式电源的规划中能够得到更多适合决策者选择的规划方案。

[1]章文俊，程浩忠，程正敏，等（ZhangWengjun，ChengHaozhong，Cheng Zhengmin，etal）．配电网优化规划研究综述（Review of distribution network optimal planning）[J]．电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2008，20（5）：16-23，55．

[2]Borges C L T，Falcao D M．Optimal distributed generation allocation for reliability，losses，and voltage improvement [J]．International Journal of Electrical Power and Energy Systems，2006，28（6）：413-420．

[3]Nara K，Hayashi Y，Ikeda K，et al.Application of Tabu search to optimal placement of distributed generators[C]// IEEE Conference on Power Engineering Society Winter Meeting.Columbus，USA，2001：918-923.

[4]Edwin Haesen，Marcelo Espinoza，Bert Pluymers，et al. Optimal placement and sizing of distributed generator units using genetic optimization algorithm[J].IEEEElectricalPowerQuality and Utilization，2005，6（1）：97-103.

[5]周杨烯，黎灿兵，何禹清，等（Zhou Yangxi，LiCanbing，He Yuqing，etal）.GSO算法在分布式电源选址与定容中的应用（Location and penetration ofdistributed generation based on group search optimizer）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（5）：58-62.

[6]陈琳，钟金，倪以信，等（Chen Lin，Zhong Jin，NiYixin，et al）.联网分布式发电系统规划运行研究（A study on grid-connected distributed generation systeMplanning and itsoperation performance）[J].电力系统自动化（Automation ofElectric Power Systems），2007，31（9）：26-31.

[7]郑漳华，艾芊，顾承红，等（Zheng Zhanghua，AiQian，Gu Chenghong，etal）.考虑环境因素的分布式发电多目标优化配置（Multi-objective allocation of distribution generation considering environmental factor）[J].中国电机工程学报（Proceedingsof the CSEE），2009，29（13）：23-28.

[8]刘学平，刘天琪，王剑（Liu Xueping，Liu Tianqi，Wang Jian）.基于小生境的配电网多目标分布式电源规划（Niche-basedmulti-objective distributed generators planning in distribution network）[J].电网技术（Power SysteMTechnology），2010，34（10）：126-130.

[9]周柏雄，章兢，刘侃（Zhou Boxiong，Zhang Jing，Liu Kan）.基于免疫克隆算法的逆变器非线性补偿（Nonlinearity compensation for inverter based on immune clonal algorithm）[J].计算机工程（Computer Engineering），2011，37（3）：238-240.

[10]廖春科，罗莉，何鸿君，等（Liao Chunke，Luo Li，He Hongjun，etal）.基于免疫克隆算法的航母编队配置研究（Research ofcolumnsofaircraftcarrier’sbuild up based on immune clonal algorithm）[J].舰船科学技术（ShipScience And Technology），2010，32（2）：91-94，137.

[11]Shang Ronghua，Jiao Licheng，Liu Fang，etal.A novel immune clonalalgorithMforMO problems[J].IEEE Trans on Evolutionary Computation，2012，16（1）：35-50.

[12]廖迎晨，甘德强，陈星莺，等（LiaoYingchen，Gan Deqiang，Chen Xingying，etal）.考虑分布式电源出力不确定性的城市电网模糊最优潮流分析（Fuzzy optimalpower flow analysis considering indeterminacy of distributed generation for urban power grid）[J].电力自动化设备（Electric Power Automation Equipment），2012，32（9）：35-39.

[13]鞠平，陈谦，熊传平，等（Ju Ping，ChenQian，Xiong Chuanping，etal）.基于日负荷曲线的负荷分类和综合建模（Load clustering and synthetic modeling based on daily load curves）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（16）：6-9.

[14]鲍冠南，陆超，袁志昌，等（Bao Guannan，Lu Chao，Yuan Zhichang，etal）.基于动态规划的电池储能系统削峰填谷实时优化（Load shift real-timeoptimization strategy of battery energy storage systeMbased on dynamic programming）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（12）：11-16.

[15]Swider D J.Compressed airenergy storage in an electricity systeMwith significant wind power generation[J].IEEE Transon Energy Conversion，2007，22（1）：95-102．

[16]王金良（Wang Jinliang）.风能、光伏发电与储能（Wind energy，photovoltaic generation and energy-storage）[J].电源技术（Chinese Journalof Power Sources），2009，33（7）：628-632.

Novel Immune ClonalAlgorithMfor Multi-types Distributed GeneratorsPlanning

WANG Jin1，CHEN Jiafei1，LIU Jiao1，XUYifan1，YANGFanghua1，TANGHao2
（1.College ofElectricaland Information Engineering，Changsha University of Science and Technology，Changsha 410114，China；2.Fengtan Hydroelectric Power Planton Chenzhou East Street in Yuanling County，Huaihua City，Hunan Province，Huaihua 419699，China）

Amulti-objective programmingmodelofdistributed generators（DG）isestablished，which gives considerations to environmental factors，generation costs，power loss and the stability of steady state voltage on the base of synthesizing timing characteristicsofDG daily outputand load.And a novel immune clonalalgorithm（NICA）is proposed to solve thismodel.The NICA uses the overall clonalnon-dominated ones，non-uniformmutation and removing Paretofront-intensive solutions to ensure the convergence speed and the uniformity ofsolution.Taking the IEEE33 bus systeMfor example，the analysis results showed that the optimal solution solved by NICA algorithMismore broad and more uniforMin Pareto-frontdistribution comparingwith the non-dominated sorting genetic algorithMII（NSGA-II），and verified the feasibility and effectivenessofNICA.

distributed generation（DG）；timing characteristic；multi-objective planning；novel immune clonalalgorithm；Pareto front

TM712

A

1003-8930（2015）09-0021-08

10.3969/j.issn.1003-8930.2015.09.04

王进（1972—），女，硕士，副教授，研究方向为电力系统优化、电网规划与运行及分布式电源规划。Email：wangjincjy@ 126.com

2013-11-28；

2014-04-09

国家自然科学基金资助项目（71071025）

陈加飞（1987—），女，硕士研究生，研究方向为电力系统运行与控制。Email：c_jiafei@163.com

刘娇（1989—），女，硕士研究生，研究方向为电力系统运行与控制。Email：friendlyjojo@163.com